扩展功能
文章信息
- 鲁薇薇, 杨永清, 李晓斌
- LU Wei-wei, YANG Yong-qing, LI Xiao-bin
- 随机变温作用下徐变对预应力混凝土梁桥结构行为的影响
- Effect of Creep on PC Girder Bridge Structural Behaviors under Randomly Changed Temperature
- 公路交通科技, 2017, 34(12): 82-89
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 82-89
- 10.3969/j.issn.1002-0268.2017.12.012
-
文章历史
- 收稿日期: 2017-04-18
我国已建大跨度PC梁桥在长期使用过程中普遍存在梁体下挠大、混凝土裂缝多等问题[1-2],给桥梁结构的安全运营埋下隐患。未能准确地把握混凝土徐变及其对桥梁结构行为的影响,是上述问题产生的原因之一[3-4]。混凝土周围环境温度变化使混凝土内部水分的干燥速率和黏滞性、水泥水化反应速率等发生改变,从而对混凝土徐变产生影响。但是目前通用徐变模型均将环境温度视为定值考虑,而忽略温度变化对徐变的影响。我国学者针对变温条件下的徐变预测方法和混凝土结构徐变效应进行研究。周红军[5]基于等效时间理论考虑温度变化对徐变的影响,提出基于等效时间域的温度徐变应力的初应变解法,并应用此方法对大体积混凝土结构的徐变效应进行分析。汪剑、方志[1]基于自然环境中混凝土箱梁桥的徐变效应测试结果和Fahmi等人建立的混凝土总变形的数学模型,提出同时考虑温、湿度变化及箱梁局部理论厚度等影响因素的徐变系数计算方法,并将其应用于PC连续刚构桥的徐变效应分析中。赵瑞鹏[6]采用B3模型就变温作用下徐变对桥梁结构应力和挠度的影响规律进行研究。刘沐宇等[7]采用CEB-FIP(1990)徐变模型,针对温、湿度变化条件下结合梁斜拉桥徐变效应进行分析。卢志芳等[8]将构建的环境温、湿度随时间变化函数嵌入CEB-FIP(1990)徐变模型,提供出可考虑桥梁所处环境中温、湿度变化影响徐变预测方法,并采用该预测方法对组合连续梁桥徐变效应进行分析。
由于研究者们就温度对徐变作用机理有着不同理解,加之试验条件等方面的限制,上述徐变效应分析中采用的徐变模型均有其特定的适用范围,对随机变温条件的适用性有待验证。另一方面,已进行的桥梁结构徐变效应研究,均未能明确变温作用下徐变对于预应力损失的影响。本研究结合自然环境条件下徐变试验数据和既有相关研究结果,对现有可考虑温度影响徐变模型的预测效果进行检验;应用比选出的徐变模型对PC连续刚构桥徐变效应进行分析,通过将获得的梁体挠度、截面应力和预应力损失结果与我国公路04桥规[9]给出结果进行比较,探讨忽略实际变温对徐变影响可能导致的桥梁结构行为估算偏差,从而为桥梁结构设计和施工提供参考。
1 随机变温条件下徐变预测模型比选由于温度环境较难形成,尤其涉及湿度条件变化时,已进行试验给出不同结果,有时甚至相互矛盾。因此,涉及环境温度影响的徐变模型比较有限。早期,Fahmi[10]基于时间-温度等效原理及叠加原理,提出预测变温条件下混凝土总变形的数学模型。BP模型[11]和B3模型[12]基于活化能概念调整了水泥水化、干燥持续、荷载持续和初始加载时间,扩展原有模型适用的温度范围,可用于计算介于-20~140 ℃之间的不同恒定温度条件下的混凝土徐变。CEB-FIP(1990)模型[13]通过在环境相对湿度影响系数和时间发展系数中引入温度作用,分别考虑不同恒定温度对徐变系数及其随时间发展规律的影响;该模型还通过引入的瞬时热徐变系数,考虑了瞬时变温对徐变系数的影响。组合徐变模型[14]在反映恒温、恒湿条件下混凝土徐变特性的基准徐变系数基础上,引入温度徐变系数和湿度徐变系数分别表征由温、湿度变化引起的混凝土徐变系数的发展。该模型通过3个独立的函数,充分考虑3个徐变系数各自涉及的主要影响因素和随时间发展规律;该模型通过3个徐变系数间不同形式的组合,提供预测不同温、湿度环境下混凝土徐变的方法。
基于时间-温度等效原理建立的徐变预测模型,仅适用于可视为热流变简单材料的混凝土[10],应用范围较小;BP模型和B3模型计算过于复杂,应用起来比较困难[1]。鉴于此,本研究结合自然环境条件下徐变试验数据和既有相关研究结果,就CEB-FIP(1990)模型和组合徐变模型对随机变温条件的适用性进行比较研究,以比选出更为适用于自然环境条件下实际桥梁结构徐变效应分析的徐变预测模型。
1.1 CEB-FIP(1990)模型考虑环境温度影响的CEB-FIP(1990)模型[13]:
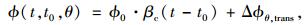
|
(1) |
式中,ϕ0为混凝土名义徐变系数;t为计算时刻的混凝土龄期;t0为混凝土的初始加载龄期;βc(t-t0)为混凝土加载后徐变随时间发展的系数;Δϕθ, trans为温度增加时刻产生的瞬时热徐变系数。
考虑温度对徐变系数影响:
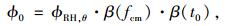
|
(2) |
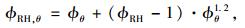
|
(3) |
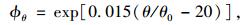
|
(4) |
式中,ϕRH为环境相对湿度影响系数,通过依赖于温度ϕRH, θ替代原来ϕRH。
考虑温度对徐变发展规律影响:
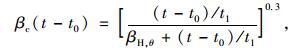
|
(5) |
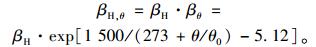
|
(6) |
式中,βH为相对湿度和构件尺寸影响系数,通过依赖于温度βH, θ替代原来βH。
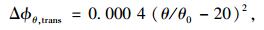
|
(7) |
式中,θ为实际固定温度;θ0=1 ℃; t=1 d。
1.2 组合徐变模型对于变温环境中混凝土的徐变,组合徐变模型[14]的数学形式为:
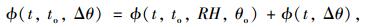
|
(8) |
式中,t为计算考虑时刻的混凝土龄期;to为混凝土初始加载龄期。
ϕ(t, to, RH, θo)为基准徐变系数,可通过既有徐变模型确定,便于比较研究,本研究分析中依据我国公路04桥规计算基准徐变系数。
ϕ(t, Δθ)为温度徐变系数:
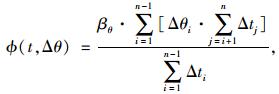
|
(9) |
式中,βθ为单位温差变化产生的温度徐变系数变化,βθ=0.04,单位为1/℃;Δθi为Δθ从ti-1到ti的Δti时间内的变化量;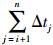
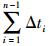
徐变试验在成都市户外自然环境条件下进行,试验用混凝土设计强度为C55,混凝土每立方米材料配比为,水泥:水:砂子:粗骨料:外加剂:粉煤灰=1:0.37:1.49:2.45:0.02:0.11。通过在自然环境中养护28 d的立方体试块和棱柱体试块,测得的试验用混凝土强度为51.6 MPa,弹性模量为3.00×104 MPa。
试验设置2组徐变试件,1组试件的加载龄期为7 d,另1组试件的加载龄期为28 d,每组3个试件。为排除混凝土温度变形、收缩变形等对徐变测试结果的影响,试验还设置了2组共计6个非持荷试件。试件形状均为圆柱体,试件和应变测试装置(振弦式传感器)的布置方式,如图 1中所示。
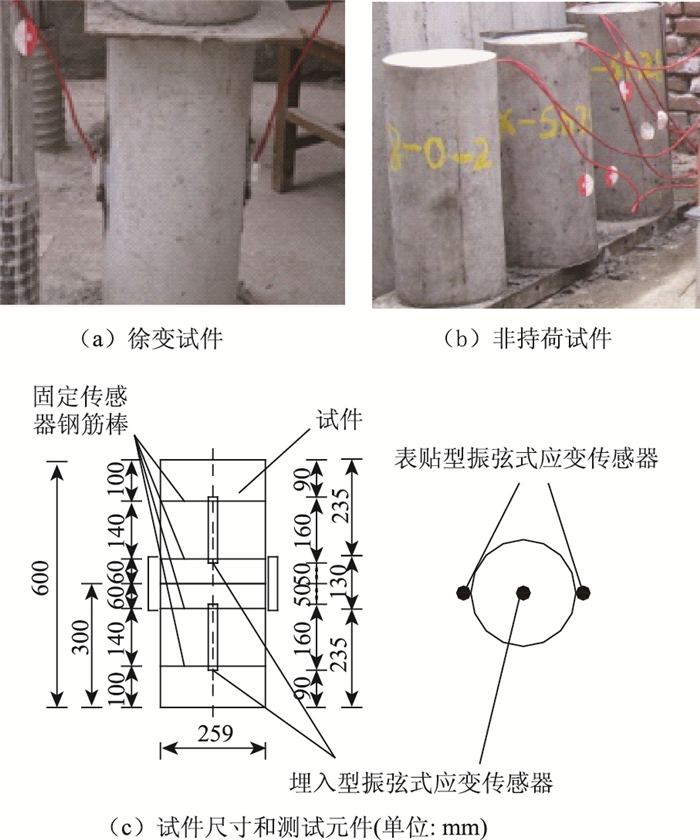
|
| 图 1 试件及振弦式应变传感器布置方式 Fig. 1 Test specimens and layout of vibrating wire strain sensors |
| |
试验中观察到,大气环境湿度变化对混凝土内部湿度影响较小,而大气温度的变化可近似等同于混凝土内温度变化。因此,自然环境条件下混凝土徐变与恒温、恒湿条件下混凝土徐变间行为差异,可视为主要由大气温度变化的影响所致。自2010年2月5日开始加载至2013年5月12日测试结束,试验共持荷1 179 d。在此期间,试验现场平均环境相对湿度为55%,大气温度历程如图 2所示。
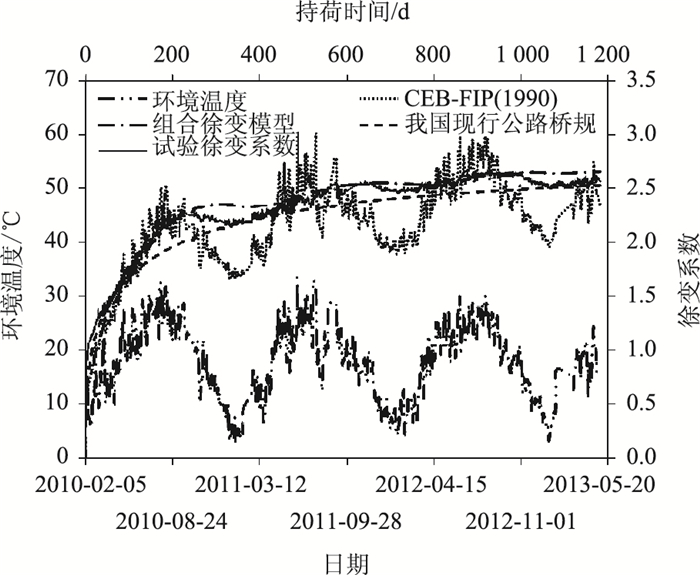
|
| 图 2 自然环境温度下徐变系数试验结果与预测结果比较 Fig. 2 Comparison of experimental and predicted creep coefficients at natural ambient temperature |
| |
由CEB-FIP(1990)模型和组合徐变模型计算得到的徐变系数与7 d加载龄期试件徐变系数的比较结果,如图 2所示。
从图 2中可以看出:与我国公路04桥规给出的徐变系数(见图 2)相比,组合徐变模型计算徐变系数与试验徐变系数的整体吻合性有所提高,平均预测偏差可减小一半以上,最大预测偏差可减小约4%;CEB-FIP(1990)模型计算徐变系数与试验徐变系数的最大偏差达24%以上,平均预测偏差约为组合徐变模型的3.5倍。
1.3.2 大气温度季节性变化对徐变影响分析Fahmi[10]和O.Ishai[15]指出,变温可导致水泥凝胶结构不可恢复变化。Havlasek[16]和Fahmi[17]研究表明,温度对徐变的影响随时间逐渐减弱。这些意味着各时刻温度改变不仅导致混凝土瞬间附加徐变产生,还会给此后徐变发展带来影响,且影响程度随时间的增长而衰减。自然环境中大气温度具有季节性变化特点,4个季节浇注混凝土经历不同变温过程,其徐变行为将有所差别。图 3中给出了由CEB-FIP(1990)模型和组合徐变模型计算得到的4个季节浇注混凝土的徐变系数发展曲线。
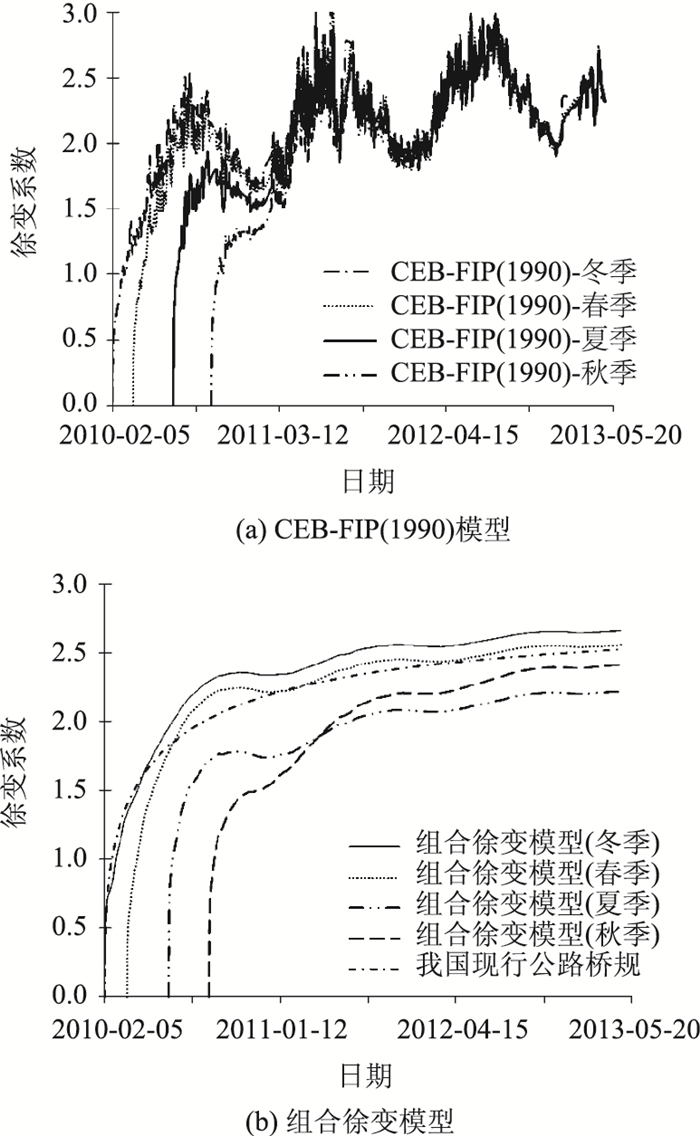
|
| 图 3 不同季节浇注混凝土的徐变系数预测结果比较 Fig. 3 Comparison of predicted creep coefficients of casted concrete in different seasons |
| |
从图 3中可以看出:CEB-FIP(1990)模型给出的4个季节浇注混凝土徐变系数曲线,除持荷初期几乎重叠在一起。组合徐变模型给出的4个季节浇注混凝土徐变系数呈现出不同的发展规律,徐变系数量值按夏季、秋季、春季和冬季浇注的顺序递增;夏季浇注混凝土的徐变系数早期发展较秋季浇注混凝土的要快,而后期则反之,这些均与Sakata等人[18]在试验中观测到结果相互吻合。
综上所述,CEB-FIP(1990)模型更适用于内部温度相对稳定的大体积混凝土等结构;组合徐变模型可以较为准确地反映出混凝土经历的温度变化历程对其徐变行为规律的影响,适用于预测温度随机变化自然环境条件下不同季节浇注混凝土的徐变发展。因此,本研究采用组合徐变模型计算PC梁桥混凝土的徐变系数。
2 混凝土徐变分析方法桥梁各构件混凝土徐变的发展受应力历程和温度历程的影响。本研究假设应力和温度变化时的徐变总变形可按相应应力增量和温度增量引起的徐变变形总和来计算。当应力和温度产生变化时,任意时刻徐变变形为:
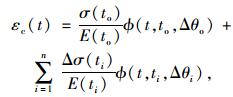
|
(10) |
式中,E(to)和E(ti)分别为to和ti龄期时的混凝土弹性模量;σ(to)为to时刻作用在构件上的应力;Δσ(ti)为ti时刻构件上的应力增量;Δθo和Δθi分别为to和ti时刻的构件混凝土周围大气环境温度变化量;ϕ(t, to, Δθo)和ϕ(t, ti, Δθi)分别为to和ti龄期时,且温度变化量为Δθo和Δθi时的构件混凝土徐变系数。
按应力历程和温度历程确定时间分界点,划分出一系列时段Δt1,Δt2,…,ΔtL-1,各时段内构件上应力和温度保持不变。根据初应变法[15],将徐变变形视为结构初始变形,用修正荷载项的方式考虑此初始变形对结构的影响。根据to时刻作用在构件上的荷载和材料性能,计算弹性应力增量Δσ1和弹性应变增量Δεe1。
由于应力和温度在此时段内保持不变,可按式(1)计算第一时段末的徐变应变增量Δεc1:
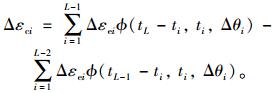
|
(11) |
再通过式(12)所示方法将作为构件初始应变的Δεc1转换为等效节点荷载ΔR1:
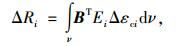
|
(12) |
式中,B为应变-位移矩阵;Ei为与时间有关的切线模量。
通过ΔR1与此刻增加的外荷载相叠加获得构件总的荷载增量,再求解Δσ2和Δεe2;结合该时刻的温度增量Δθ2,依照式(11)计算得到Δεc2。重复以上计算过程,即可得到各构件在不同时段的Δσi,Δεei,Δεci和ΔRi,从而可应用有限元法进行自然环境温度条件下桥梁结构徐变效应分析。
3 PC连续刚构桥徐变效应分析本研究基于组合徐变模型和我国公路04桥规采用的徐变模型对恒载作用下PC连续刚构桥的徐变效应进行分析,并将获得的成桥后梁体挠度、截面应力和预应力损失结果进行比较。
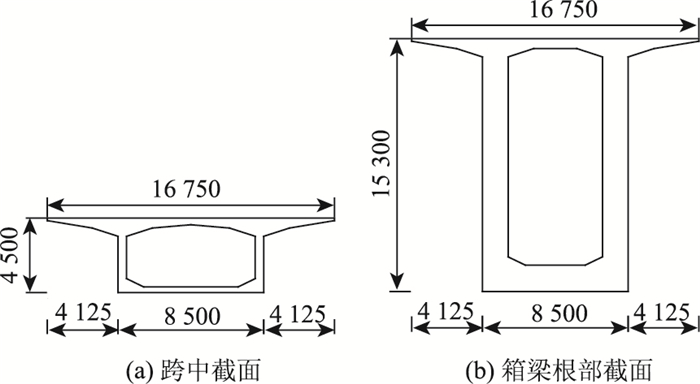
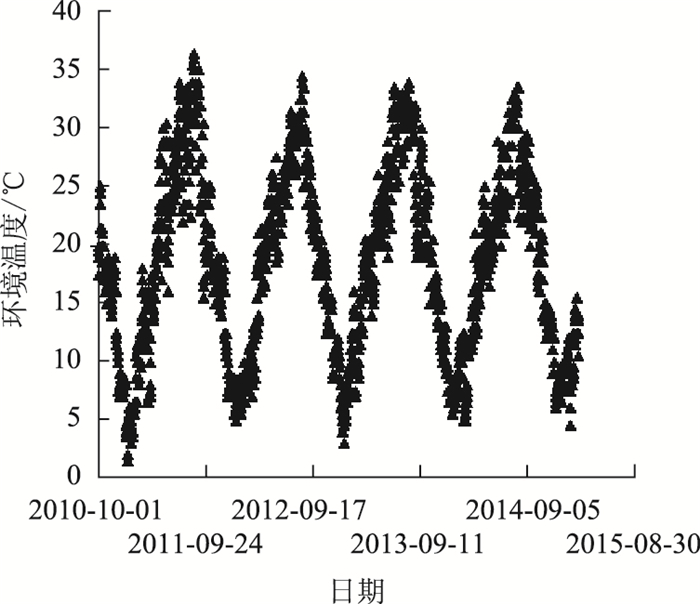
3.1 桥梁概况及有限元模型某跨径组合为(138.5+245+138.5)m连续刚构桥,主梁为PC变截面箱梁,箱梁跨中和根部截面如图 4所示。桥用混凝土标号为C55,预应力束采用ϕs15.2 mm高强低松弛钢绞线,标准强度为1 860 MPa,张拉控制应力为1 395 MPa。桥址位于重庆北碚地区,该地区在2010年10月至2015年8月期间每天平均大气温度(来源于天气网)如图 5所示,根据桥址地区气象资料,环境平均相对湿度按70%考虑。
|
| 图 4 箱梁跨中和根部截面图(单位:mm) Fig. 4 Mid-span and support cross-sections of box girder (unit: mm) |
| |
|
| 图 5 桥址处自然环境温度历程 Fig. 5 Natural temperature history at bridge site |
| |
PC连续刚构桥有限元模型,如图 6所示。主梁按实际梁段(每个梁段内截面变化处也划分单元)划分为178个单元,桥墩划分为32个单元。桥墩处0#和1#梁段为托架施工,2#~35#梁段为挂篮分节段对称悬臂浇注施工,每边跨支架现浇段长14.18 m,全桥设有2个边跨合龙段和1个中跨合龙段,先合龙边跨再合龙中跨,共计43个施工阶段,各梁段混凝土初始加载龄期为5 d。
|
| 图 6 有限元模型 Fig. 6 Finite element model |
| |
3.2 组合徐变模型计算程序
计入自然环境温度影响,使构件混凝土徐变系数计算工作更为繁杂。为此,本研究采用计算机语言编制组合徐变模型计算程序。该计算程序中主程序负责输入数据,调用两子程序和外部函数,执行式(8)的计算过程;两子程序分别完成基本徐变系数和温度徐变系数的计算工作;外部函数向两子程序提供计算所需时间参数。计算程序中仅温度徐变系数子程序的算法与以往不同,其计算流程如图 7所示。
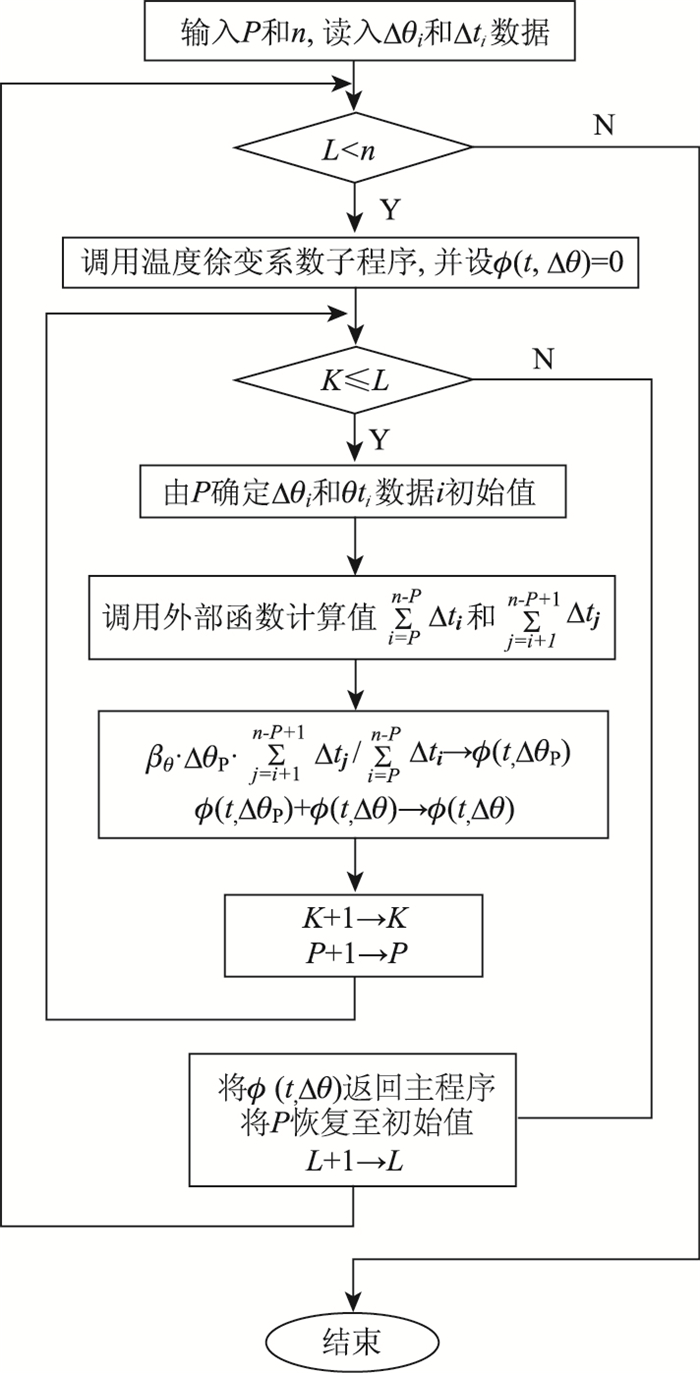
|
| 图 7 温度徐变系数子程序流程图 Fig. 7 Flowchart of temperature creep coefficient subprogram |
| |
图 7中变量P为构件生成日期与Δt1对应日期间天数差;n为时段划分数量,时段的分界点依据桥梁施工和运营过程中结构边界条件、荷载的改变以及环境温度历程确定;L和K为循环变量,其他参数同前文。
3.3 结果分析图 8和表 1中所示为成桥后各计算时间相对于成桥时梁体挠度变化的比较结果;成桥后主梁截面应力的比较结果,列于表 2中;图 9和表 3中提供了预应力损失的比较结果。
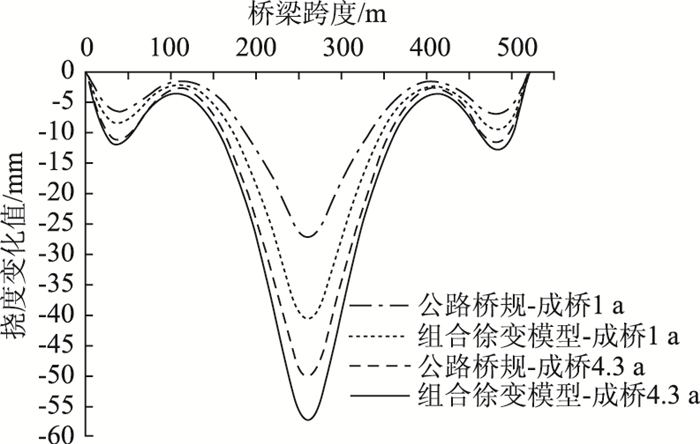
|
| 图 8 成桥后挠度变化结果比较 Fig. 8 Comparison of deflections after bridge constructed |
| |
| 计算时间/a | 边跨跨中 | 主跨跨中 | |||||
| 公路04桥规 | 组合徐变模型 | 差值 | 公路04桥规 | 组合徐变模型 | 差值 | ||
| 1 | -4.1 | -5.4 | -1.3 | -25.1 | -40.6 | -15.5 | |
| 2 | -5.3 | -5.5 | -0.2 | -34.7 | -41.0 | -6.3 | |
| 3 | -6.1 | -6.2 | -0.1 | -41.2 | -45.9 | -4.7 | |
| 4 | -6.7 | -7.3 | -0.6 | -45.9 | -54.8 | -8.9 | |
| 4.3 | -6.8 | -7.6 | -0.7 | -46.9 | -57.3 | -10.4 | |
| 注:挠度为各计算时间相对于成桥时挠度变化值;表中差值为考虑环境温度影响后增加的梁体挠度;负值为挠度向下。 | |||||||
| 计算时间/a | 边跨跨中截面 | 主跨跨中截面 | |||||||
| 公路04桥规 | 组合徐变模型 | 公路04桥规 | 组合徐变模型 | ||||||
| 上缘 | 下缘 | 上缘 | 下缘 | 上缘 | 下缘 | 上缘 | 下缘 | ||
| 1 | -7.37 | -7.09 | -7.47 | -6.68 | -7.79 | -6.43 | -8.19 | -5.78 | |
| 2 | -7.35 | -7.03 | -7.38 | -6.76 | -7.86 | -6.18 | -8.11 | -5.79 | |
| 3 | -7.34 | -7.00 | -7.36 | -6.75 | -7.90 | -6.05 | -8.14 | -5.68 | |
| 4 | -7.33 | -6.98 | -7.39 | -6.65 | -7.92 | -5.97 | -8.24 | -5.47 | |
| 4.3 | -7.32 | -6.98 | -7.40 | -6.62 | -7.92 | -5.96 | -8.27 | -5.41 | |
| 注:负值表示压应力。 | |||||||||
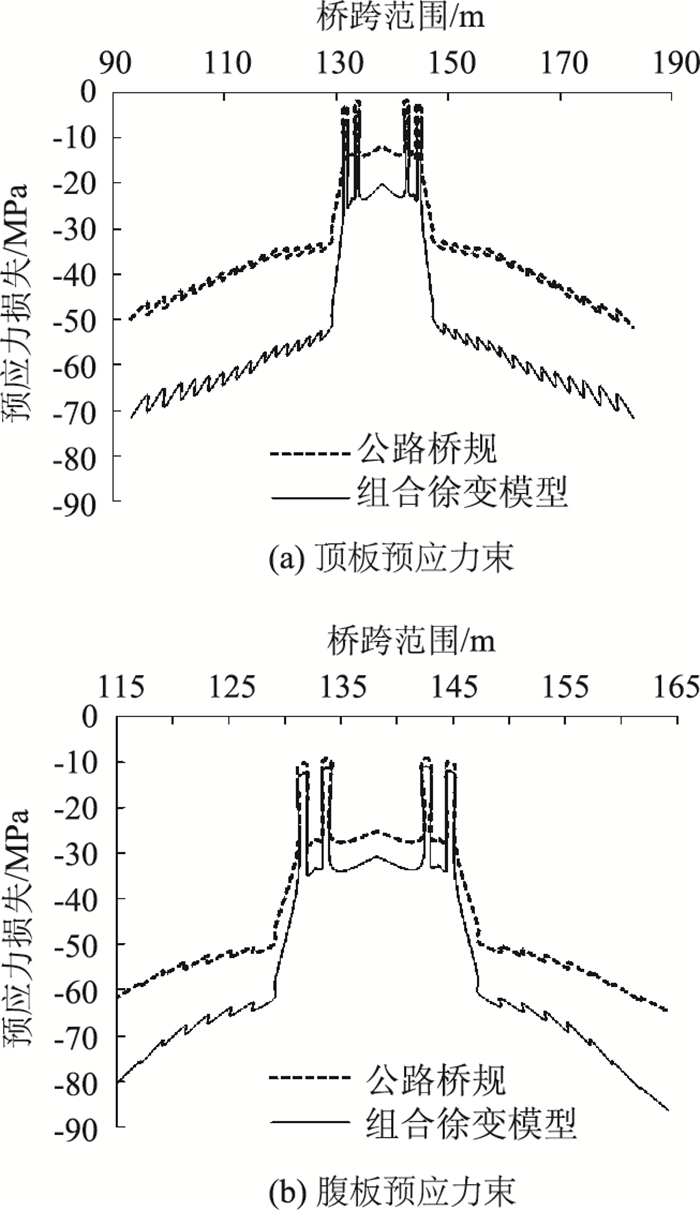
|
| 图 9 徐变引起的预应力损失结果比较 Fig. 9 Comparison of prestressing losses caused by concrete creep |
| |
| 钢束 | 徐变模型 | 1 a | 2 a | 3 a | 4.3 a |
| 边跨底板束 | 公路04桥规 | -25 | -29 | -31 | -34 |
| 组合徐变模型 | -29 | -32 | -36 | -41 | |
| 中跨底板束 | 公路04桥规 | -34 | -42 | -46 | -49 |
| 组合徐变模型 | -30 | -35 | -39 | -44 | |
| 顶板束 | 公路04桥规 | -42 | -47 | -50 | -52 |
| 组合徐变模型 | -62 | -66 | -69 | -72 | |
| 腹板束 | 公路04桥规 | -52 | -58 | -62 | -65 |
| 组合徐变模型 | -74 | -79 | -82 | -86 |
由比较结果可以得出的结论如下:
(1) 自然环境温度影响下的徐变加剧成桥后梁体下挠(见图 8),成桥后各计算时间,主梁边跨跨中下挠度增加了约2%~32%,主梁中跨跨中下挠度增加了约11%~62%;受自然环境温度季节性变化的影响,增加的梁体挠度并不随时间增长而单调变化,在分析中呈先减后增的趋势(见表 1)。
(2) 计入自然环境温度影响的混凝土徐变,导致主梁边、中跨跨中截面下缘压应力减小,上缘压应力增大。受自然环境温度季节性变化的影响,截面下缘减少(上缘增加)的压应力随时间而起伏变化。成桥后各计算时间,下缘减少压应力介于-0.37~-0.65 MPa之间,上缘增大压应力在-0.25~-0.40 MPa范围变化,比较结果详见表 2。
(3) 由图 9和表 3可知,考虑自然环境温度影响的混凝土徐变,主梁顶板预应力束的应力损失增加了约38%~48%,主梁腹板预应力束的应力损失增加了约32%~42%;而主梁边、中跨底板预应力束受到的影响相对较小,预应力束的应力损失增加或减少不超过21%。自然环境温度影响下混凝土徐变,对不同部位预应力束的应力损失表现出不同的影响规律,这主要由预应力束布置梁段混凝土经历的温度历程及预应力作用时间的差异所致。
4 结论本研究结合试验数据和既有研究,就现有可考虑温度影响的徐变模型对随机变温条件的适用性进行检验;应用比选出的组合徐变模型,对自然环境温度影响下PC梁桥徐变效应进行分析,并与我国公路04桥规进行比较研究,获得以下结论:
(1) 由组合徐变模型提供的考虑实际变温影响的徐变系数预测结果与试验结果最为贴近,与我国公路04桥规相比,平均预测偏差可减小50%以上,最大预测偏差可减小约4%。
(2) 同我国公路04桥规相比,自然环境温度影响下混凝土徐变导致主梁边跨跨中下挠度增加0.1~1.3 mm,中跨跨中下挠度增加4.7~15.5 mm,使主梁中(边)跨跨中截面下缘压应力最多减小5%(1%),上缘压应力最多增加10%(6%)。
(3) 布置梁段混凝土浇注季节及预应力作用时间,对预应力损失影响明显;自然环境温度影响下徐变引起的预应力损失基本上较规范值要大,成桥4.3 a后主梁腹板、顶板束的应力损失较规范值大40%以上,主梁边(中)跨底板束的应力损失较规范值大(小)不超过21%(17%)。
(4) 自然环境温度影响下的混凝土徐变,加剧了桥梁梁体持续下挠、混凝土开裂和预应力损失等问题,给桥梁结构的耐久性和长期使用性带来非常不利的影响。在桥梁结构设计和施工中,推荐采用组合徐变模型计入实际环境温度对结构混凝土徐变的影响,从而为预应力束的合理布置与张拉控制、梁体预拱度的准确设置等提供参考。
| [1] |
汪剑, 方志. 大跨预应力混凝土箱梁桥收缩徐变效应测试与分析[J]. 土木工程学报, 2008, 41(1): 70-81. WANG Jian, FANG Zhi. Analysis and Field Measurement of Concrete Box Girder Bridges for Shrinkage and Creep Effects[J]. China Civil Engineering Journal, 2008, 41(1): 70-81. |
| [2] |
王威. 徐变对混凝土连续梁桥状的影响分析[D]. 兰州: 兰州交通大学, 2012. WANG Wei. Analysis on Influence of Creep on State of Concrete Continuous Beam Bridges[D]. Lanzhou:Lanzhou Jiaotong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10732-1012449423.htm |
| [3] |
曾丁, 谢峻, 郑晓华, 等. 桥梁短期实测数据修正高强混凝土收缩徐变模型与长期挠度预测[J]. 公路交通科技, 2014, 31(11): 72-77. ZENG Ding, XIE Jun, ZHENG Xiao-hua, et al. Prediction of Long-term Deflection and Correction of Shrinkage and Creep Model of High-strength Concrete of Bridge Based on Measured Short-term Data[J]. Journal of Highway and Transportation Research and Development, 2014, 31(11): 72-77. |
| [4] |
袁明, 颜东煌. 基于预应力混凝土组合单元的PC连续箱梁桥混凝土徐变效应研究[J]. 公路交通科技, 2012, 29(10): 38-53. YUAN Ming, YAN Dong-huang. Concrete Creep Effect of PC Continuous Box Girder Bridge Based on PC Composite Unit[J]. Journal of Highway and Transportation Research and Development, 2012, 29(10): 38-53. |
| [5] |
周红军. 温度对混凝土徐变影响的数值模型[D]. 南京: 河海大学, 2004. ZHOU Hong-jun. Numerical Model for Concrete Considering Influence of Temperature on Creep[D]. Nanjing:Hohai University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10294-2004050505.htm |
| [6] |
赵瑞鹏. 混凝土桥梁温度徐变效应与耦合效应分析研究[D]. 西安: 长安大学, 2010. ZHAO Rui-peng. Study on Temperature Creep Effect and Coupling Effect on Concrete Bridge[D]. Xi'an:Chang'an University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-11941-2010220696.htm |
| [7] |
刘沐宇, 袁卫国, 刘伟方, 等. 温湿变化对三塔结合梁斜拉桥徐变效应的影响研究[J]. 武汉理工大学学报:交通科学与工程版, 2013, 37(5): 900-903. LIU Mu-yu, YUAN Wei-guo, LIU Wei-fang, et al. Study on the Creep Effect of Composite Girder Cable-stayed Bridge with Three-tower under the Changing Temperature-humidity[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2013, 37(5): 900-903. |
| [8] |
卢志芳, 刘沐宇, 李倩. 考虑温度和湿度变化的钢-混组合连续梁桥徐变效应分析[J]. 中南大学学报:自然科学版, 2015, 46(7): 2650-2657. LU Zhi-fang, LIU Mu-yu, LI Qian. Creep Effect Analysis of Steel-concrete Composite Bridge Considering Mutative Temperature and Relative Humidity[J]. Journal of Central South University:Science and Technology Edition, 2015, 46(7): 2650-2657. |
| [9] |
JTG D62-2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62-2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [10] |
FAHMI H M. Time-dependent Behavior of Concrete under Sustained Load and Cyclic Temperature[D]. Berkeley:University of California, 1971.
|
| [11] |
BAZANT Z P, KIM J K. Improved Prediction Model for Time-dependent Deformations of Concrete:Part 4-Temperature Effects[J]. Materials and Structures, 1992, 25(2): 84-94. |
| [12] |
BAZANT Z P, MURPHY W P. Creep and Shrinkage Prediction Model for Analysis and Design of Concrete Structures Model B3[J]. Materials and Structures, 1995, 29(2): 126-126. |
| [13] |
Euro-International Committee for Concrete. CEB-FIP Model Code 1990:Design Code[S]. London:Thomas Telford, 1990.
|
| [14] |
杨永清, 鲁薇薇, 李晓斌, 等. 自然环境混凝土徐变试验和预测模型研究[J]. 西南交通大学学报, 2015, 50(6): 977-983, 1010. YANG Yong-qing, LU Wei-wei, LI Xiao-bin, et al. Experimental Study and Prediction Model for Concrete Creep in Ambient Environment[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 977-983, 1010. |
| [15] |
黄国兴, 惠荣炎, 王秀军. 混凝土徐变与收缩[M]. 北京: 中国电力出版社, 2012. HUANG Guo-xing, HUI Rong-yan, WANG Xiu-jun. Concrete Creep and Shrinkage[M]. Beijing: China Electric Power Press, 2012. |
| [16] |
HAVLASEK P, JIRASEK M. Modeling of Concrete Creep Based on Microprestress-solidification Theory[J]. Acta Polytechnica, 2012, 52(2): 34-42. |
| [17] |
FAHMI H M, POLIVKA M, BRESLER B. Effect of Sustained and Cyclic Elevated Temperature on Creep of Concrete[J]. Cement and Concrete Research, 1972, 2(5): 591-606. |
| [18] |
SAKATA K, AYANO T. Effect of Ambient Temperature and Humidity on Creep and Shrinkage of Concrete[C]//Adam Neville Symposium:Creep and Shrinkage Structural Design Effects. Atlanta:American Concrete Institute, 2000:215-235. https://www.concrete.org/publications/internationalconcreteabstractsportal/m/details/id/9894
|
 2017, Vol. 34
2017, Vol. 34
