扩展功能
文章信息
- 龙刚, 刘永健, 朱伟庆, 封博文
- LONG Gang, LIU Yong-jian, ZHU Wei-qing, FENG Bo-wen
- PBL加劲型矩形钢管混凝土桁架拱桥设计
- Design of Rectangular CFST Truss Arch Bridge Stiffened with PBL
- 公路交通科技, 2017, 34(12): 51-58
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 51-58
- 10.3969/j.issn.1002-0268.2017.11.008
-
文章历史
- 收稿日期: 2016-12-16
2. 西安市政设计研究院有限公司, 陕西 西安 710068
2. Xi'an Municipal Engineering Design & Research Institute Co., Ltd., Xi'an Shaanxi 710068, China
随着我国交通建设的飞速发展,高等级公路不仅在经济发达的东部地区密布组网,而且逐渐向西部山区延伸。作为公路中跨越障碍的关键部分,桥梁结构也不断朝着造型新颖,或大跨度、重载化等方向发展。而钢管混凝土拱桥具有施工方便、受力合理、跨越能力强的特点,因此在我国得到了广泛的应用[1-3]。但是,钢管与混凝土之间的组合效应主要取决于两者之间的界面性能。受混凝土收缩、徐变等的影响,服役期间钢管混凝土界面黏结应力很有可能被克服而脱空;进一步受日照温差、混凝土浇注质量的影响,其脱空程度可能更大[4-6]。钢管与混凝土之间脱空后会严重影响拱肋的受力性能:对于钢管混凝土拱肋节段,在轴向压力作用下,钢管对混凝土的套箍作用减弱,而钢管则更早发生屈曲,可能使得构件的实际承载力甚至低于设计强度[7-11];对于拱肋节点,立柱沿拱肋轴线方向的力由钢管向核心混凝土的传递需要更长的传递长度[12-13],并可能导致拱肋钢管在立柱作用下产生应力集中、甚至发生屈曲[14-16]。而随着桥梁使用、美观等方面功能的不断增多,造型较为复杂的,如景观拱桥等也较多地出现,受力复杂的某些构件及节点往往会发生应力集中[16-18]。
为了避免或者尽量减少以上问题的出现,论文第二作者提出在钢管混凝土拱肋中设置开孔钢板(PBL)纵肋,以期加强钢管与混凝土的组合作用并改善节点区域传力性能,从而形成一种新型的桥梁结构——PBL加劲型钢管混凝土拱桥。这一新型桥梁结构形式已经成功应用在西宁市海湖新区跨湟水河景观桥工程某在建桥梁中。结合该桥梁的设计方案,在主桥结构分析、节点分析等基础上,分析这一新桥型的特点和优势,以期推动其发展和应用。
1 西宁市某景观桥主桥结构设计 1.1 桥梁设计标准及功能要求(1) 桥梁设计标准
① 荷载标准:人群荷载4.0 kN/m2;②地震设防烈度:7度;地震动峰值加速度:0.10g;设计特征周期为0.45 s;③桥梁设计洪水频率100 a一遇;④桥梁设计基准期为100 a,设计安全等级为一级。
(2) 桥梁设计功能要求
本桥为跨湟水河人行景观桥,要求设计桥型有一定的跨越能力和泄洪能力;该桥需连接位于下层的湟水河两侧河堤路和位于上层的河南侧规划景观一级平台及河北侧亲水公园路;且需保证与当地景观的协调。同时,本桥位于青海省西宁市区。根据我国《公路桥涵设计通用规范》(JTG D60—2015),西宁市为严寒地区。其气候特点为干燥多风、日照温差大、冬季寒冷、冻融作用严重。因此,对桥梁在温度作用、冻融作用下的可靠性均有较高的要求。
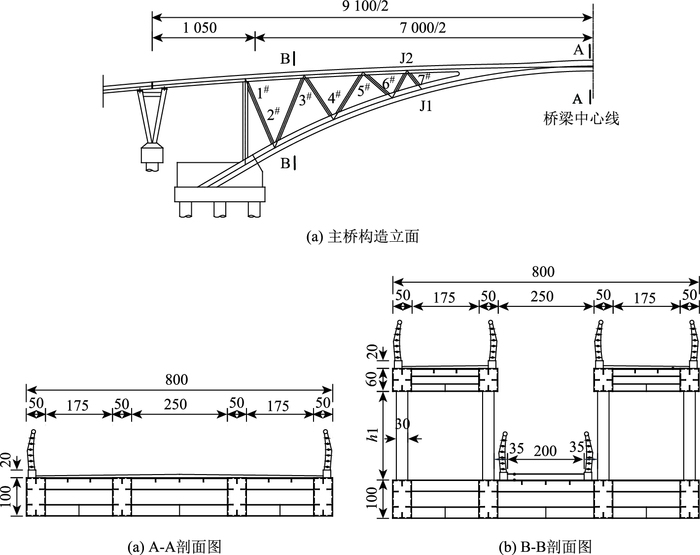
1.2 主桥结构设计为了满足桥梁的设计标准和功能的要求,将主桥的桥型方案综合确定为钢管混凝土桁架拱桥,设上、下两层桥面(图 1)。下层主要受力结构为主拱肋,采用PBL加劲型矩形钢管混凝土,下层桥面铺设于主拱圈横梁上,用于连接湟水河两侧河堤路。上层受力结构为梁肋,采用矩形钢管,上层桥面铺设于梁肋上,用于连接河南侧规划景观一级平台及河北侧亲水公园路。同时,下层桥面自拱脚沿拱圈逐渐上升与上层桥面“合二为一”(图 2),上、下结构采用矩形钢管腹杆联系在一起形成桁架-拱结构。各杆件截面形式均采用矩形截面,可方便进行杆件的融合,并方便进行构件的加工和焊接, 保证施工质量。

|
| 图 1 桥梁总体效果图 Fig. 1 Rendering of bridge |
| |
|
| 图 2 上部结构构造图(单位:cm) Fig. 2 Structure of superstructure (unit: cm) |
| |
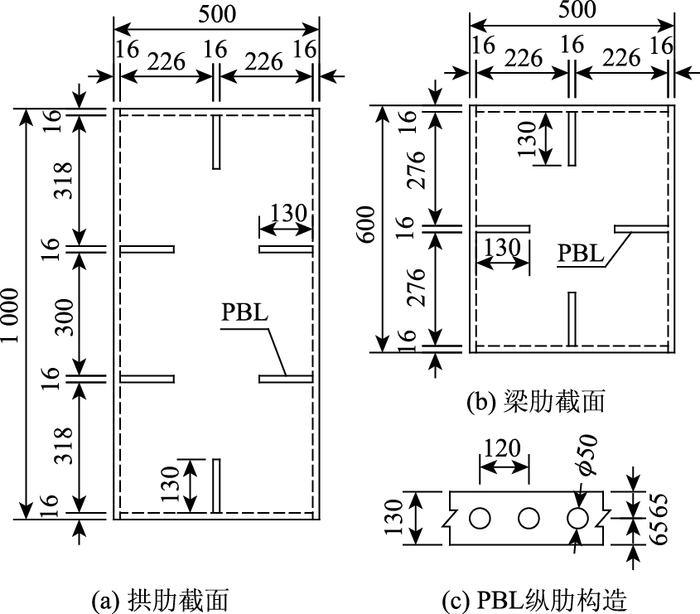
结合实际地形情况、路线设计标高等,主桥结构设计具体阐述如下(见图 2):主桥全长91 m,总宽8 m。下层拱肋采用半径为69.2 m的圆弧拱轴线,圆弧对应圆心角为61°,计算矢高为9.5 m,拱肋的矢跨比约为1:7.4。横向拱肋共4片,边-中拱肋中距2.5 m,中-中拱肋中距3 m。下层拱肋截面采用1 000 mm×500 mm×20(16) mm焊接箱型截面,管内灌注C50混凝土。为加强拱肋钢管与混凝土的组合作用,并改善腹杆与拱肋间节点传力,管内设PBL纵肋,肋高130 mm,厚16 mm,开孔孔径50 mm,开孔间距120 mm。上层梁肋与拱肋宽度相同且沿竖向对齐,梁肋截面为600 mm×500 mm×16 mm焊接箱型截面。梁肋截面与拱肋截面在拱顶附近采用共腹板的形式合并,实现上下层桥面合二为一。腹杆采用300 mm×300 mm×12 mm焊接箱型截面。腹杆与梁肋的节点位置在梁肋内部灌注混凝土以改善节点受力性能。主拱拱脚与预埋在承台内部的钢板焊接。立柱截面采用800 mm×500 mm×20(16) mm,内灌C50微膨胀混凝土,立柱与拱肋采用共腹板的形式连接。梁肋与立柱内设置PBL纵肋,而腹杆内设置普通加劲肋(如图 3)。
|
| 图 3 拱肋、梁肋断面构造(单位:mm) Fig. 3 Cross-section of arch rib and beam rib (unit: mm) |
| |
2 主桥结构分析
采用MIDAS/Civil建立主桥的整体系杆有限元模型(见图 4)。主桥下层拱肋、上层梁肋、腹杆、立柱和横梁采用梁单元模拟,桥面板采用板单元。对于PBL加劲型钢管混凝土拱肋,在建立结构整体有限元模型时,梁单元偏于安全地不考虑PBL纵肋。由于全桥节点为全焊接节点,故采用共节点模拟。

|
| 图 4 主桥有限元模型 Fig. 4 Finite element model of main bridge |
| |
2.1 主拱肋受力分析
表 1给出了内侧拱肋不同荷载组合时的钢管与混凝土的应力,以拉应力为正,压应力为负。由表 1可知:(1)在恒载与活载组合时,下层拱肋以受压为主;虽然接近拱脚的部位作用有较小的负弯矩,靠近拱顶的部位有一定的正弯矩,但是整个拱肋处于全截面受压。(2)系统升、降温对拱肋的应力影响较大;恒载、活载与系统降温的组合为最不利组合工况,此工况下,拱脚截面产生较大的负弯矩,混凝土上缘有一定的拉应力,而拱顶截面产生较大的正弯矩,混凝土下缘有一定的拉应力。(3)拱肋各截面的应力满足材料强度要求(本节中数值分析为弹性分析,在组合Ⅱ和组合Ⅲ作用下,拱脚和拱顶(弯矩较大)附近截面边缘混凝土出现拉应力;由于出现拉应力的混凝土范围很小,而且钢管应力水平不高,同时考虑到拱脚和拱顶附近的刚度剧烈变化也可能引起计算模拟失真,因此可认为这一小范围的混凝土拉应力不会对主桥承载力造成影响)。
| 荷载类型 | 位置 | 拱脚截面 | 1/4拱截面 | 7#腹杆处拱截面 | 拱顶截面 | |||||
| 钢管 | 混凝土 | 钢管 | 混凝土 | 钢管 | 混凝土 | 钢管 | 混凝土 | |||
| 恒载 | 上缘 | -12.05 | -1.91 | -7.035 | -1.235 | -6.04 | -0.911 | -18.75 | -3.065 | |
| 下缘 | -21.35 | -3.68 | -19.35 | -3.185 | -18.55 | -3.205 | -0.621 | -0.179 | ||
| 活载 | 上缘 | -4.095 | -0.63 | -1.865 | -0.327 | -1.69 | -0.279 | -9.475 | -1.53 | |
| 下缘 | -6.675 | -1.18 | -7.505 | -1.245 | -7.29 | -1.225 | 2.885 | 0.423 5 | ||
| 组合Ⅰ | 恒+活 | 上缘 | -15.7 | -2.48 | -8.83 | -1.55 | -7.65 | -1.19 | -28.4 | -4.62 |
| 下缘 | -28.7 | -4.96 | -26.77 | -4.43 | -25.75 | -4.43 | 2.4 | 0.28 | ||
| 组合Ⅱ | 恒+活+升温 | 上缘 | -77.3 | -10.54 | -14.4 | -0.43 | -13.1 | -0.08 | -21.65 | -1.509 |
| 下缘 | 19.5 | 4.98 | -35.4 | -3.79 | -34.5 | -3.74 | -15.15 | -0.511 | ||
| 组合Ⅲ | 恒+活+降温 | 上缘 | 46 | 5.54 | -3.27 | -2.68 | -2.29 | -2.28 | -35.16 | -7.74 |
| 下缘 | -76.8 | -14.86 | -18.13 | -5.06 | -17.13 | -5.12 | 20.04 | 1.06 | ||
| 包络 | 压应力 | -77.3 | -14.86 | -35.4 | -5.06 | -34.5 | -5.12 | -35.16 | -7.74 | |
| 拉应力 | 46 | 5.54 | — | — | — | — | 20.04 | 1.06 | ||
2.2 桁架拱体系受力分析
桁架拱桥的杆件包括立柱、斜腹杆和上层梁肋等空钢管杆件,以及下层PBL加劲型矩形钢管混凝土拱肋,各杆件主要以受轴向力为主。连接上层梁肋与下层拱肋的腹杆采用“人”字形布置。腹杆作为传力构件,将上部结构自重及荷载传递给下弦拱肋,同时将整个结构连接成整体,使整个桁架结构共同受力。同样,当荷载直接作用于拱肋时,通过腹杆将荷载传递到结构各处,减少拱肋受力,使桁架整体受力合理。
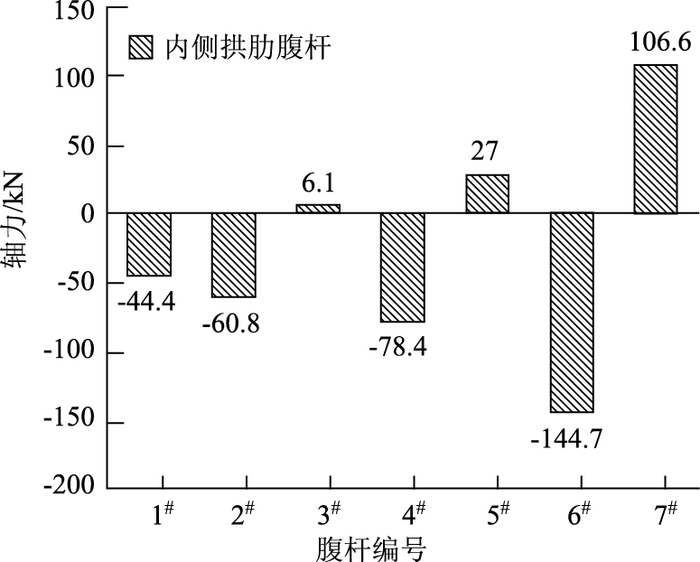
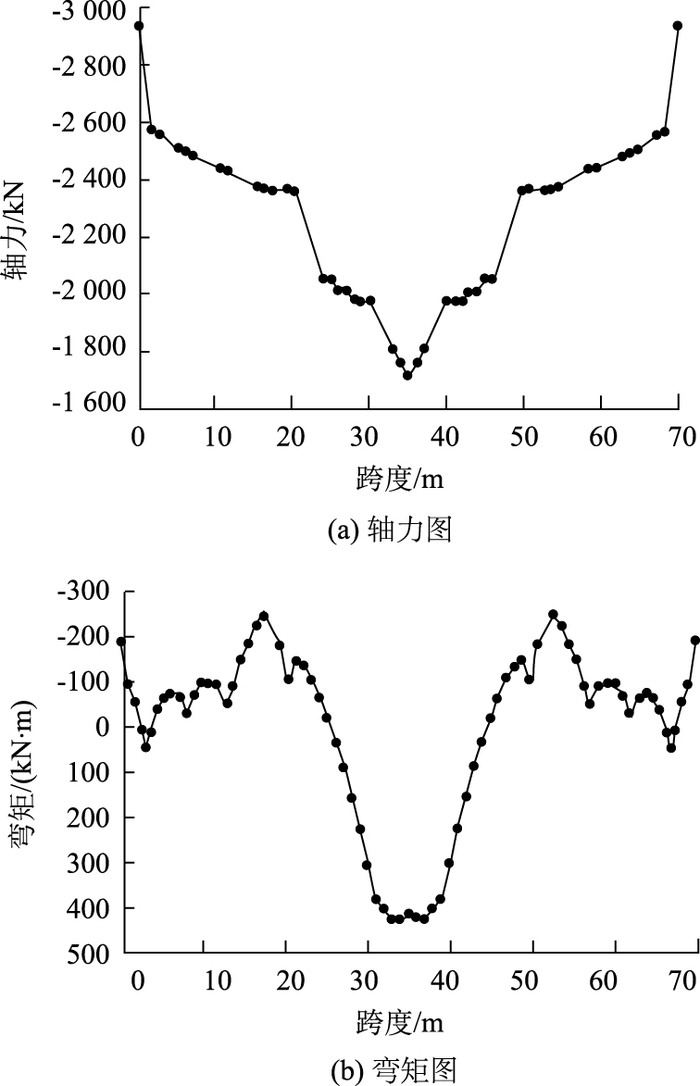
图 5为恒载与活载组合时各腹杆的轴力图,图 6和图 7分别为恒载与活载组合时的梁肋与拱肋的轴力和弯矩沿主桥跨度的变化情况。由图 5可知,恒载与活载作用下,1#,2#,4#,6#为压杆,3#,5#,7#为拉杆,且靠近拱顶的腹杆的轴力明显较大;由图 6(a)可知,梁肋在靠近拱顶附近时的轴向压力最大,此后迅速变小,且在受力最大的6#和7#腹杆附近变小的速率最快,此后变化速率明显变小;由图 7(a)可知,拱顶的拱肋轴向压力最小,此后迅速增大并拱肋轴力在拱脚达到最大。同样,拱肋轴力增大速率在拱顶至6#和7#腹杆处最大。针对这种现象,可作如下分析:
|
| 图 5 内侧拱肋腹杆轴力图 Fig. 5 Axial forces of inside arch rib web members |
| |
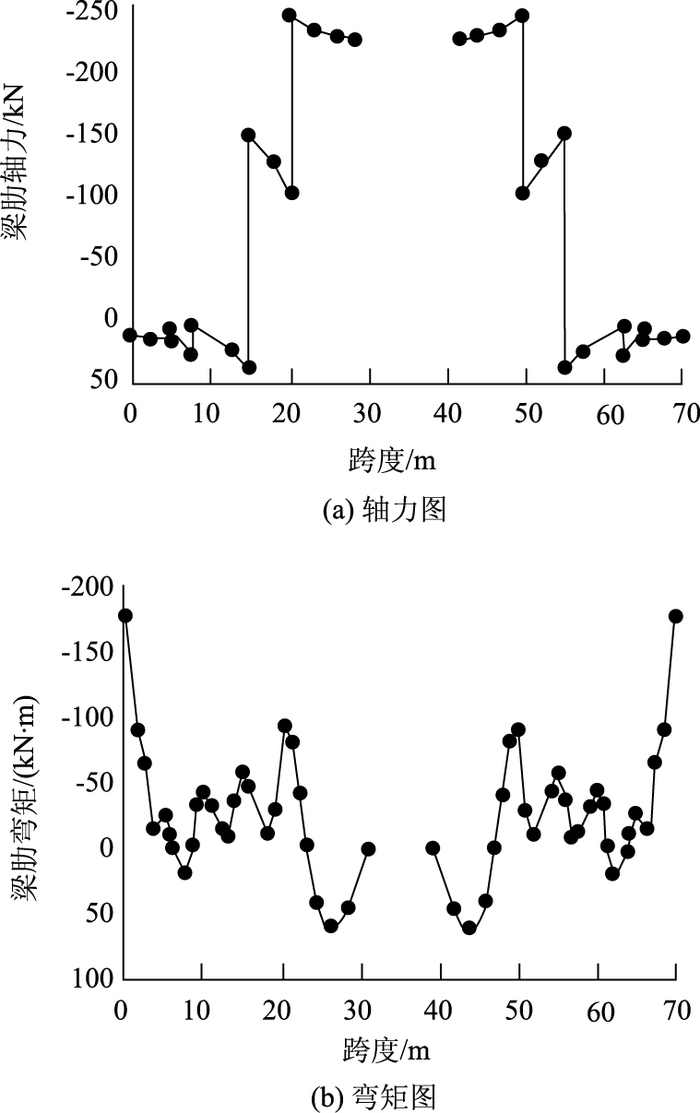
|
| 图 6 内侧梁肋内力图 Fig. 6 Internal force of inside beam rib |
| |
|
| 图 7 内侧拱肋内力图 Fig. 7 Internal force of inside arch rib |
| |
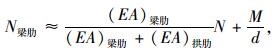
|
(1) |
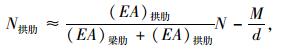
|
(2) |
式中,N和M分别为整个截面的轴力和弯矩;d为拱肋与梁肋中心的距离。根据拱肋和梁肋的材料和截面几何性质,式(1)和式(2)可转化为:
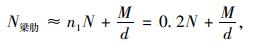
|
(3) |
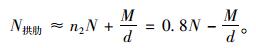
|
(4) |
由于接近拱顶跨中附近,整个截面的轴力N相对其他区域小、弯矩M相对较大,因此,由式(3)和式(4)可知此时梁肋轴力N梁肋主要由M决定,其值相对其他区域较大;拱肋轴力N拱肋则由N和M共同决定,相对其他区域较小。同理,在远离拱顶部位的过程中,整个截面轴力N逐渐变大,而弯矩M迅速变小,因此,由式(3)和式(4)可知,此时梁肋的轴力迅速变小,而拱肋的轴力迅速变大。而梁肋与拱肋之间的力由腹杆传递,在梁肋与拱肋轴力变化最快的位置,腹杆(6#和7#)的轴力也较大,而且呈“拉-压”的组合。
在接近拱脚的部位,整个截面轴力N达到最大,M达到最小。因此由式(3)和式(4)可知,梁肋轴力很小,而拱肋轴力达到最大。梁肋此时以承受上层结构自重和桥面荷载,以受弯为主;而腹杆在此区域主要为压力,甚至呈“压-压”组合,此时,梁肋与腹杆的受力接近多跨连续刚构体系(可由图 5腹杆轴力图和图 6(b)梁肋靠近拱脚部位的弯矩图得到验证——1#和2#腹杆均为压杆;梁肋在1#和2#腹杆中间有较大的正弯矩,而在立柱以及2#腹杆附近存在较大的负弯矩)。而拱肋不仅承受下层结构的自重及下层桥面荷载,而且还需承受由腹杆传来的上层结构自重及上层桥面荷载。经验算,梁肋与腹杆应力水平不高,均满足设计要求。
3 节点分析选取腹杆受力较大的节点进行局部精细化有限元分析,包括拱肋节点J1和梁肋节点J2(如图 2(a))。采用有限元分析软件,针对J1,J2节点分别建立设置PBL纵肋、设置普通直肋、不设置加劲肋的3种模型,以对比设置PBL纵肋对节点受力的影响。由于节点区域构造复杂,部分单元划分不规则,为了使得计算结果更准确,钢管采用S4R四节点减缩积分壳单元模拟,PBL纵肋与混凝土采用C3D8R八节点减缩积分六面体单元模拟。钢管与混凝土的界面接触模型由钢与混凝土截面的法向硬接触和切向黏结滑移构成,采用PBL纵肋单元嵌入混凝土主单元中模拟PBL纵肋与混凝土的相互作用。
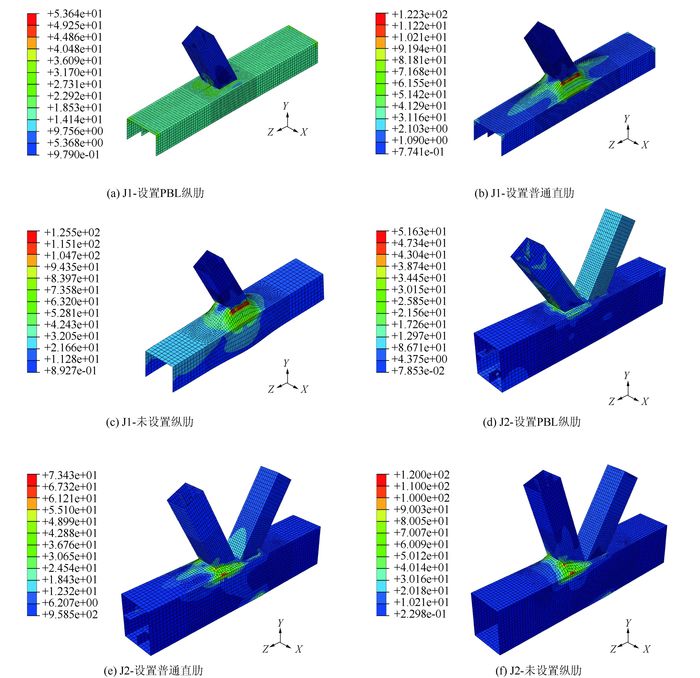
分析计算结果如图 8和表 2所示。由此可知,对于节点J1和节点J2,有如下结论:(1)设置PBL纵肋的节点支、主管应力水平均较其他两类节点大幅降低,应力集中程度明显减缓;(2)设置PBL纵肋的节点,主管钢管的变形尤其是鼓曲程度明显变小;(3)根据节点附近钢管的应力和变形特点可知,设置PBL纵肋的节点中,支管传来的剪力在由主管钢管向核心混凝土传递时,传递长度明显变短。因此,设置PBL纵肋能明显改善节点的应力和变形状况,并提高节点的抗疲劳性能。
|
| 图 8 J1,J2节点应力状态(单位:MPa) Fig. 8 Stress state of joint J1 and joint J2(unit:MPa) |
| |
| 节点 | 设置PBL 纵肋 | 设置普通 直肋 | 不设置 纵肋 | |
| J1 | 最大应力/MPa | 53.64 | 122.3 | 125.5 |
| 鼓曲变形/mm | 0.083 | 0.44 | 0.58 | |
| J2 | 最大应力/MPa | 51.63 | 73.43 | 120 |
| 鼓曲变形/mm | 0.017 | 0.22 | 0.4 | |
4 拱肋钢管与混凝土界面分析
由于拱肋受力较大,故选取拱肋截面进行计算。太阳辐射作用下钢管与混凝土间的界面作用分析分为热传导计算及结构脱空计算两个部分。其中热传导计算中,设置PBL纵肋的拱肋中钢管、PBL及管内混凝土均采用DC3D4四节点线性传热四面体单元模拟,其他拱肋中钢管、加劲肋及管内混凝土均采用DC3D8八节点线性传热六面体单元模拟。模型中考虑太阳直接辐射、钢管表面对流换热及辐射换热3种热交换方式,钢管与环境的接触采用第3类边界条件,钢与混凝土接触采用第4类边界条件。而结构脱空计算是在前者计算结果的基础上,取前者计算得到的最不利温度场(根据夏季7月某一天(早上6:00初始温度取12.9 ℃)的数值计算结果,下午14:00时拱肋截面温度梯度达到最大)进行计算。结构脱空计算部分的建模方法与第4节中相同;同时,由于钢管与混凝土之间的径向黏结力较小,且对结算计果影响较小,因此,钢管与混凝土的径向相互作用中忽略两者径向黏结力。
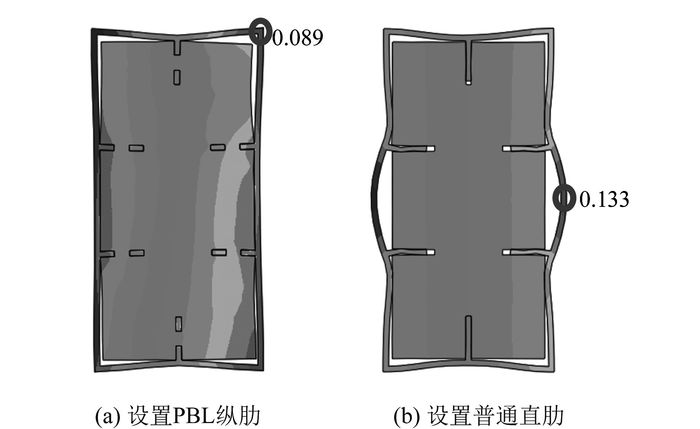
计算分析结果如图 9。由图可以发现,设置普通纵肋的拱肋沿界面均有较大程度的脱空,且在两加劲肋中部位置脱空最为严重(0.133 mm);而由于PBL纵肋与混凝土之间形成的混凝土榫能加强钢管与混凝土的组合作用,设置PBL纵肋的拱肋中钢管与混凝土的脱空现象明显得到缓解,其仅在拱肋角部有0.089 mm的变形。因此,设置PBL纵肋能明显改善由于钢管与混凝土之间的脱空程度,改善拱肋在运营阶段的受力性能和安全。
|
| 图 9 太阳辐射下拱肋钢管与混凝土脱空(单位:mm) Fig. 9 Debonding between steel tube and concrete under solar radiation (unit: mm) |
| |
5 结论
(1) 采用PBL加劲型矩形钢管混凝土桁架拱桥的设计方案不仅满足桥梁的设计标准与使用功能的要求,且与环境协调,造型美观,受力较为合理,整体应力水平不高,满足安全的要求。
(2) 设置PBL纵肋能明显减小受力复杂的钢管混凝土拱肋节点的传力长度,改善节点的受力和变形集中程度。同时,设置PBL纵肋能明显缓解拱肋在太阳辐射作用下的钢管与混凝土的脱粘和脱空。
| [1] |
陈宝春. 钢管混凝土拱桥[M]. 2版. 北京: 人民交通出版社, 2007. CHEN Bao-chun. Concrete Filled Steel Tubular Arch Bridges [M]. 2nd ed. Beijing: China Communications Press, 2007. |
| [2] |
李亚东, 姚昌荣, 梁艳. 浅论拱桥的技术进步与挑战[J]. 桥梁建设, 2012, 42(2): 13-20. LI Ya-dong, YAO Chang-rong, LIANG Yan. On Technical Advancement and Challenge of Arch Bridges[J]. Bridge Construction, 2012, 42(2): 13-20. |
| [3] |
CHEN B C, WANG T L. Overview of Concrete Filled Steel Tube Arch Bridges in China[J]. Practice Periodical on Structural Design and Construction, 2009, 14(2): 70-80. |
| [4] |
郑强, 孙国安. 佛陈大桥缺陷原因分析及加固[J]. 中国铁道科学, 2000, 21(4): 21-29. ZHENG Qiang, SUN Guo-an. Defects Analysis and Reinforcement of Fochen Bridge[J]. China Railway Science, 2000, 21(4): 21-29. |
| [5] |
傅斌, 许晓锋, 黄福伟. 对钢管混凝土拱桥病害的调研及分类[J]. 公路工程与运输, 2008(4): 220-223. FU Bin, XU Xiao-feng, HUANG Fu-wei. The Diseases Investigation and Classification of Concrete Filled Steel Tubular Arch Bridges[J]. Communications Standardization, 2008(4): 220-223. |
| [6] |
付文胜, 田洪松, 孙仲. 基于钢管混凝土拱桥检测结果的主拱肋病害评估[J]. 桥梁建设, 2013, 43(1): 47-51. FU Wen-sheng, TIAN Hong-song, SUN Zhong. Assessment of Deteriorations of Main Arch Ribs of CFST Arch Bridge Based on Inspection Results[J]. Bridge Construction, 2013, 43(1): 47-51. |
| [7] |
刘振宇, 陈宝春. 钢管混凝土桁拱热脱粘及温度应力分析[J]. 公路交通科技, 2011, 28(7): 67-72. LIU Zhen-yu, CHEN Bao-chun. Analysis on Thermal Debonding and Stress of CFST Truss Arch[J]. Journal of Highway and Transportation Research and Development, 2011, 28(7): 67-72. |
| [8] |
涂光亚, 颜东煌, 邵旭东, 等. 脱粘对桁架式钢管混凝土拱肋刚度影响研究[J]. 公路交通科技, 2011, 28(2): 93-110. TU Guang-ya, YAN Dong-huang, SHAO Xu-dong, et al. Effect of Debonding on Stiffness of Trussed Concrete-filled Steel Tubular Arch Rib[J]. Journal of Highway and Transportation Research and Development, 2011, 28(2): 93-110. |
| [9] |
唐述. 脱空钢管混凝土构件力学性能研究[D]. 广州: 广州大学, 2011. TANG Shu. Study on Mechanical Properties of Separation Concrete Filled Steel Tubular Members[D]. Guangzhou:Guangzhou University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-11078-1012262821.htm |
| [10] |
杨世聪, 王福敏, 渠平. 核心混凝土脱空对钢管混凝土构件力学性能的影响[J]. 重庆交通大学学报:自然科学版, 2008, 27(3): 360-365. YANG Shi-cong, WANG Fu-min, QU Ping. Brief Introduction to the Core Concrete's Empty Influence on the Mechanical Performance of Concrete Filled Steel Tube Components[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2008, 27(3): 360-365. |
| [11] |
程高. PBL加劲型矩形钢管混凝土轴压柱承载力计算方法研究[D]. 西安: 长安大学, 2013. CHEN Gao. Calculation on Bearing Capacity of CFST Column Stiffened with PBL under Axial Load[D]. Xi'an:Chang'an University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10710-1014022951.htm |
| [12] |
刘永健, 李慧, 张宁, 等. PBL加劲型矩形钢管混凝土界面粘结-滑移性能[J]. 建筑科学与工程学报, 2015, 32(5): 1-7. LIU Yong-jian, LI Hui, ZHANG Ning, et al. Interface Bond-slip Performance of Rectangular Concrete-filled Steel Tube Stiffened by PBL[J]. Journal of Architecture and Civil Engineering, 2015, 32(5): 1-7. |
| [13] |
刘永健, 张宁, 张俊光. PBL加劲型矩形钢管混凝土的力学性能[J]. 建筑科学与工程学报, 2012, 29(4): 13-17. LIU Yong-jian, ZHANG Ning, ZHANG Jun-guang. Mechanical Behavior of Concrete-filled Square Steel Tube Stiffened with PBL[J]. Journal of Architecture and Civil Engineering, 2012, 29(4): 13-17. |
| [14] |
刘永健, 李慧, 张宁. 非均匀受压矩形钢管混凝土局部弹性屈曲分析[J]. 建筑科学与工程学报, 2015, 32(4): 1-8. LIU Yong-jian, LI Hui, ZHANG Ning. Local Elastic Buckling Analysis of Rectangular Concrete-filled Steel Tube under Non-uniform Compression[J]. Journal of Architecture and Civil Engineering, 2015, 32(4): 1-8. |
| [15] |
LIU Y J, XIONG Z H, LUO Y L, et al. Double-composite Rectangular Truss Bridge and Its Joint Analysis[J]. Journal of Traffic and Transportation Engineering, 2015, 2(4): 249-257. |
| [16] |
程高, 刘永健, 田智娟, 等. PBL加劲型矩形钢管混凝土不等宽型节点受拉性能[J]. 长安大学学报:自然科学版, 2015, 35(3): 83-90. CHEN Gao, LIU Yong-jian, TIAN Zhi-juan, et al. Tensile Behavior of PBL Stiffened Concrete-filled Rectangular Steel Tubular Unequal T-connections[J]. Journal of Chang'an University:Natural Science Edition, 2015, 35(3): 83-90. |
| [17] |
程高, 刘永健, 邱洁霖, 等. PBL加劲型矩形钢管混凝土不等宽型节点应力集中系数分析[J]. 建筑科学与工程学报, 2014, 31(4): 74-79. CHEN Gao, LIU Yong-jian, QIU Jie-lin, et al. Analysis of Stress Concentration Factor on Concrete-filled Rectangular Steel Tube T-joints Stiffened with PBL[J]. Journal of Architecture and Civil Engineering, 2014, 31(4): 74-79. |
| [18] |
张宁, 刘永健, 刘士林, 等. 单孔PBL剪力连接件疲劳性能试验研究[J]. 建筑结构学报, 2014, 35(3): 186-192. ZHANG Ning, LIU Yong-jian, LIU Shi-lin, et al. Experimental Study on Fatigue Behavior of Single PBL Shear Connector[J]. Journal of Building Structures, 2014, 35(3): 186-192. |
 2017, Vol. 34
2017, Vol. 34
