扩展功能
文章信息
- 王伟, 朱慈祥, 李少芳, 苏云超
- WANG Wei, ZHU Ci-xiang, LI Shao-fang, SU Yun-chao
- 环氧树脂-混凝土叠合结构的热应力分析
- Analysis on Thermal Stresses in Epoxy-concrete Laminated Structure
- 公路交通科技, 2017, 34(12): 44-50
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 44-50
- 10.3969/j.issn.1002-0268.2017.12.007
-
文章历史
- 收稿日期: 2016-11-24
环氧树脂在混凝土桥面、钢桥面甚至路面的使用非常普遍[1],然而研究发现,环氧树脂的线性热膨胀系数一般在50~100×10-6 (m·m-1)/℃[2]左右,而混凝土的线性热膨胀系数为8.5~11.7×10-6 (m·m-1)/℃[3],在温度变化时会因变形不协调而造成相容性差的问题,最终导致破坏[4]。Sprinkel[5]、David[6]等人提出造成环氧树脂-混凝土叠合结构破坏的主要原因是环氧树脂较高的固化收缩率以及比混凝土高至少一倍的线性热膨胀系数。DongUK Choi[7]等人研究了环氧树脂-混凝土叠合结构中环氧树脂层正应力、界面剪应力、界面法向力的大小和分布规律,并指出该应力大小的主要影响因素是环氧覆层材料的弹性模量以及铺设厚度,且一般较小的弹性模量和铺设厚度出现破坏的几率较低。Negheimish A.I.[8]等人提出环氧树脂-混凝土叠合结构的破坏不能仅仅归因于高速路面的载荷或超载,而是在均匀降温时端部的局部范围内会出现应力集中,且在靠近界面的混凝土内部产生较大的拉应力,同时指出在基础混凝土强度较好时热应力不会造成破坏。上述研究归结了环氧树脂-混凝土叠合结构产生破坏的主要原因和使用时温度应力的计算,但并没有涉及环氧树脂在固化过程中收缩应力、固化应力、后固化应力的计算方法。本文针对环氧树脂-混凝土叠合结构在不同的养护温度、固化温度、使用温度以及后固化温度等条件下的热应力情况,采用理论分析、模型试验和有限元计算等方式给出了不同条件下环氧树脂层中应力的计算公式,为环氧树脂-混凝土叠合结构的热应力计算提供了理论基础,也为环氧树脂材料的选材、施工及养护提供参考。
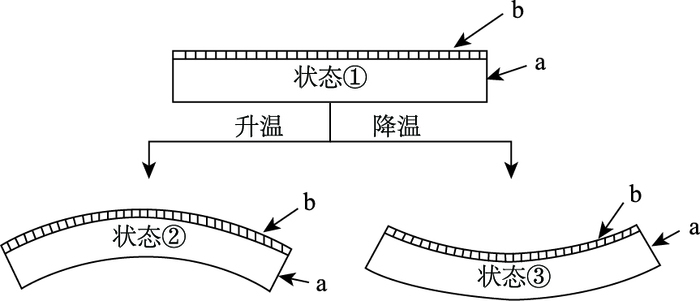
1 环氧树脂-混凝土叠合结构热应力计算方法 1.1 热应力基本公式环氧树脂直接浇注在混凝土表面时,由于环氧树脂收缩、环境温度的变化,引起环氧树脂相对混凝土的膨胀/收缩,而在环氧树脂-混凝土叠合结构中产生应力[9]。如图 1为环氧树脂-混凝土叠合结构模型在温度变化时的变形趋势[10],其中a表示混凝土,b表示环氧树脂。
|
| 图 1 环氧树脂-混凝土叠合结构受温度影响的变形示意图 Fig. 1 Schematic diagram of deformation of epoxy resin-concrete laminated structure due to temperature change |
| |
从图 1中可以看出,在初始温度一定时,体系体积稳定(如状态①,即b的绝对长度等于a),内部没有应力;当体系温度上升时,由于环氧砂浆线性热膨胀系数大于混凝土材料,其受热膨胀值大于混凝土(即b的绝对长度大于a),表现为状态②;当体系温度下降时,则会表现为状态③(即b的绝对长度小于a)。
实际上,环氧树脂-混凝土叠合结构自浇注开始,就会因各种原因而产生应力累积[11],如:环氧树脂固化过程中的应力累积、不同固化温度的应力累积、高温后固化的应力累积,以及使用过程中的应力累积(仅考虑降温的情况),这些应力分为收缩应力、固化应力、后固化应力、温度应力4类。
J.W. Hutchinson[12]等人总结了不同线性热膨胀系数的材料复合时其内部因升降温而造成的约束应力的计算公式,如式(1):
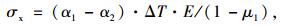
|
(1) |
式中,σx为环氧树脂层中的应力;α1为环氧层的线性热膨胀系数;α2为混凝土基层的线性热膨胀系数;ΔT为整体温度变化;E1为环氧层的弹性模量;μ1为环氧层的泊松比。
从式(1)中可以看出,由于线性热膨胀系数不同,任何温度的变化都会产生σx,即在环氧树脂内部产生累积应力。基于此,提出了收缩应力、固化应力、后固化应力、温度应力的计算方法,如下所述。
1.2 收缩应力收缩应力即固化收缩过程中累积的应力,用符号σs表示。当环氧树脂在固化过程中,会因混凝土的约束而产生应力。设环氧树脂的固化收缩率为εs(固化收缩率为时间t的函数),而在从液态到最终固化的过程中,环氧树脂的弹性模量为Es(弹性模量为时间t的函数)[13-14],则在恒温固化期间,环氧树脂内部累积的应力可由式(2)表示:
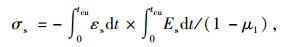
|
(2) |
式中,εs为环氧树脂的常温固化收缩率;Es为环氧树脂的弹性模量;tcu为环氧树脂常温固化时间。
1.3 固化应力即固化过程中,因不同温度养护(非使用温度)造成的应力,用符号σcu表示。环氧树脂浇注后,若养护温度与使用温度不同,如:环氧树脂在养护温度Tcu下完成固化,降温/升温至使用温度Tu时,环氧树脂会因与混凝土变形量不同而受到混凝土的约束产生应力。设环氧树脂固化后的弹性模量为E(E在Tcu至Tu范围内随着温度变化而变化,为温度T的函数),则其内部累积的应力可由式(3)表示:
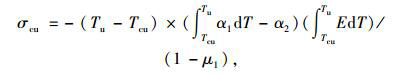
|
(3) |
式中:Tu为环氧树脂使用温度;Tcu为环氧树脂养护温度;E为在Tcu至Tu范围内环氧树脂弹性模量。
1.4 后固化应力后固化应力即常温完全固化的环氧树脂,在高温后固化时因二次固化收缩造成的应力,用符号σpc表示。
环氧树脂在常温固化时的强度、弹性模量、热变形温度、固化收缩率均大于高温固化后的材料[15],如:常温固化后抗拉弹性模量为2 000 MPa,热变形温度为58 ℃的环氧树脂,在经受100 ℃高温加热后,其抗拉模量变为2 800 MPa,热变形温度变为80 ℃,且环氧树脂体积会因为后固化收缩而有所降低,这种现象称为环氧树脂的后固化。基于这一特性,常温固化(养护温度与使用温度相同)的环氧树脂-混凝土叠合结构在经受高温处理后,会由于后固化收缩产生的体积变化而造成环氧树脂中产生应力,该应力还与环氧树脂的热变形温度变化、线性热膨胀系数变化以及弹性模量变化有关,其应力大小可由式(4)表示(其中Tht>Th>Tl>Tu):
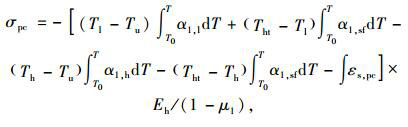
|
(4) |
式中,Tu为环氧树脂使用温度;Tl为环氧树脂常温固化时的热变形温度;Th为环氧树脂高温后固化之后的热变形温度;Tht为环氧树脂后固化温度;Eh为环氧树脂后固化后的弹性模量;α1, l为常温固化时低于热变形温度的线性热膨胀系数;α1, h为高温后固化时低于热变形温度的线性热膨胀系数;α1, sf为高于热变形温度时的线性热膨胀系数;εs, pc为高温后固化时的收缩率。
1.5 温度应力即环氧树脂固化后(不考虑1.3和1.4中情况)因温度升、降而产生的应力,用符号σtm表示。
当环氧-混凝土体系完全固化后(假定使用温度Tu为一固定温度),在温度偏离Tu时(如变温至Tch),会因环氧与混凝土变形不协调而造成温度应力[16],其大小可由式(5)表示:
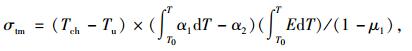
|
(5) |
式中,Tu为环氧树脂使用温度;Tch为环氧树脂升、降温后温度;E为在Tch至Tu范围内环氧树脂的弹性模量。
1.6 总热应力从以上计算可以看出,在环氧树脂浇注到混凝土上开始,“环氧树脂-混凝土”结构就因各种因素导致的变形不协调而产生内部应力,在最不利的环境温度下,环氧树脂中最大应力σALL可由式(6)计算:

|
(6) |
为研究上述4类应力情况,采用ASTM C884《Standard Test Method for Thermal Compatibility Between Concrete and an Epoxy-Resin Overlay》[17]所述试验方法中的试件(但环氧树脂中不掺集料),在混凝土与环氧树脂上布设应变片[18],测试不同养护温度,以及温度变化条件下体系中的应力情况。
2.1 试验养护流程试验所采用的试件按照ASTM C884中描述的方法制作,养护条件如表 1所示,其中σx为环氧树脂中测试部位的正应力,σz混凝土中测试部位的正应力。
| 编号 | 测试应力类型 | 养护流程 | 测试流程 | |
| σx | σz | |||
| 1 | σs | σs, z | 浇注后即置于23 ℃室内空气中养护7 d | 从浇注开始对粘贴应变片部位进行测试,直至试件出现裂缝,或者应变不再变化时,停止试验。 |
| 2 | σcu | σcu, z | 浇注后即置于60 ℃烘箱中养护3 d,后置于23 ℃的室内空气中养护4 d | |
| 3 | σpc | σpc, z | 浇注后即置于23 ℃室内空气中养护7 d后,置于100 ℃烘箱中养护4 h后置于23 ℃室内空气中继续养护3 d | |
| 4 | σtm | σtm, z | 23 ℃室内空气中养护7 d后放入-20 ℃空气中养护7 d | |
2.2 原材料及应变片布设位置
(1) 环氧树脂材料:本次试验采用两种模量相差较大的环氧树脂,其主要性能见表 2。
| 编号 | 线胀系数α1/ [×10-5(m·m-1)·℃-1] | 弹性模量E/ MPa | 抗拉强度/ MPa | 断裂伸长 率/% |
| M1 | 9.0 | 55 | 13.4 | 51.6 |
| M2 | 6.0 | 2 800 | 35.2 | 2.5 |
(2) 混凝土:采用普通硅酸盐水泥以0.28的水灰比拌制的C50混凝土,砂率为34%,其主要性能参数见表 3。
| 强度等级 | 水灰比 | 砂率 | 28 d抗压 强度/MPa | 28 d抗拉拔 强度/MPa | 抗拉弹性 模量/MPa |
| C50 | 0.28 | 34% | 63.1 | 4.5 | 25 126 |
(3) 应变片布置
在混凝土4个侧面以及环氧树脂顶面和底面粘贴应变片,如图 2所示,应变片基底尺寸为15 mm×4 mm。所有混凝土应变片均在环氧树脂浇注之前粘贴(环氧树脂顶部应变片在树脂固化后粘贴),同时对每一个养护流程都设置空白控制试件(在随温度自由变化的环氧树脂以及混凝土上均布设应变片),对测试结果进行修正。图 3和图 4为应变片布置和浇注后的环氧树脂。

|
| 图 2 应变片粘贴布置图 Fig. 2 Layout of strain gauges |
| |

|
| 图 3 应变片布置 Fig. 3 Layout of strain gauges |
| |

|
| 图 4 环氧树脂浇注后 Fig. 4 Epoxy resin casted on concrete |
| |
3 试验结果分析
为了便于结果分析,在剔除变异点之后,将4个侧面,以及每面对称部位结果进行平均处理,并以数字1~5进行编号(如图 2所示),环氧树脂上粘贴应变片取平均值,且规定受拉时应变为正,受压时应变为负,通过补偿修正后按前述规定取值。其中由于液态环氧树脂无法粘贴应变片,流程1仅仅测试σs, z,并未测试σs。
3.1 M1环氧树脂测试结果试验中,流程1,2,3的应变测试结果较小,且变化无规律,认为在这3个流程下,混凝土中应力较小,几乎可以忽略不计。主要原因是M1树脂的弹性模量在常温非常小,仅为55 MPa,随着温度的升高模量进一步降低,而高温后固化对其性能影响较小,从而导致体积变化时的应力累积很小。
图 5为M1树脂在降温流程4下的应变-时间曲线,从图中可以看出,随着温度的下降,混凝土中开始累积应变,当冷冻时间为1.5 h左右时,累积应变开始显著增加,最终在260 142 s时混凝土出现裂缝,此时混凝土中最大应变为170×10-6,其应力约为4.27 MPa。
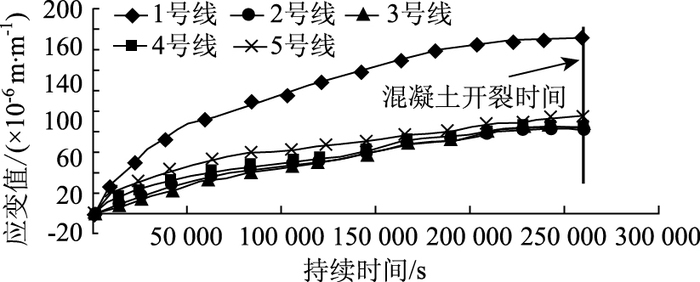
|
| 图 5 M1树脂流程4混凝土各部位应变-时间图 Fig. 5 Strain-time curves of concrete for casting epoxy resin M1 under process 4 |
| |
3.2 M2环氧树脂测试结果
从图 6中可以看出,随着流程1的进行,混凝土中开始累积拉应变并快速增大,当固化进行到10 h左右时,应变停止增长,表明在常温下环氧树脂已固化完毕,在环氧树脂体积不发生改变的情况下单纯强度的增大不会造成混凝土中出现应变,最终1号部位的最大应变为28×10-6,其应力约为0.70 MPa。
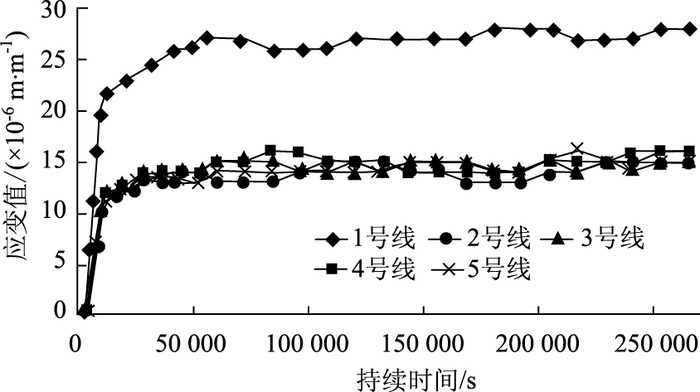
|
| 图 6 M2树脂流程1混凝土各部位应变-时间图 Fig. 6 Strain-time curves of concrete for epoxy resin M2 under process 1 |
| |
从图 7中可以看出,当试件从烘箱中拿出来那一刻,混凝土中就迅速累积了拉应变,随着时间的增长趋势有所放缓,但仍在持续增大,当1号位应变达到134×10-6 m/m时,混凝土开裂,体系累积的应力释放,混凝土在整个过程中的最大拉应力为3.37 MPa。
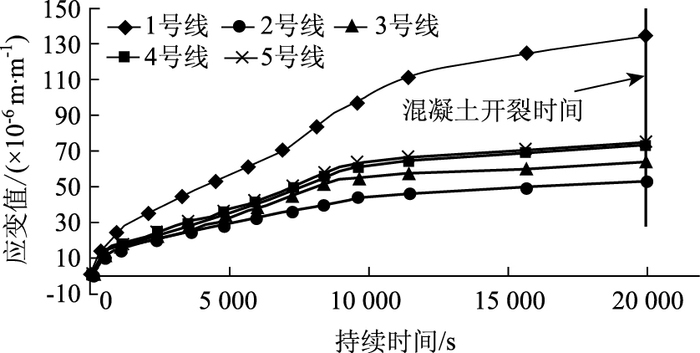
|
| 图 7 M2树脂流程2混凝土各部位应变-时间图 Fig. 7 Strain-time curves of concrete for epoxy resin M2 under process 2 |
| |
从图 8中我们可以看出,在升温过程中,混凝土中的最大拉应变变化比较复杂,当升温温度小于环氧树脂常温固化的热变形温度时,混凝土中的拉应变为负值,表明混凝土处于受压状态,而当升温超过环氧树脂常温固化的热变形温度时,由于环氧树脂的弹性模量的急剧下降,混凝土的应力累积迅速下降且接近于零,随着温度的进一步上升,混凝土中的最大应力一直处于“零”状态,但此时环氧树脂的热变形温度已经升高,随着试件置于常温环境,体系温度迅速下降,在温度下降至高温固化的热变形温度附近时,混凝土中迅速表现为较大压应变状态,当温度下降到一定值时,混凝土中的压应变又开始降低向拉应变转换,并最终在13×10-6 m/m时左右停止变化,此时混凝土中边角处表现为微拉应变状态,最大拉应力约为0.33 MPa。
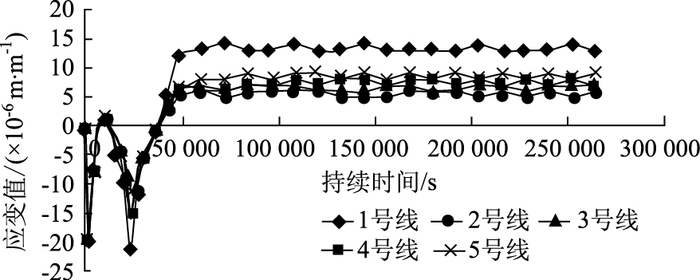
|
| 图 8 M2树脂流程3混凝土各部位应变-时间图 Fig. 8 Strain-time curves of concrete for epoxy resin M2 under process 3 |
| |
从图 9中可以看出,随着温度的下降,混凝土中迅速累积拉应变,随着时间的增加趋势有所放缓,在进行至5.53 h时,混凝土出现开裂,且最大拉应变为146×10-6m/m,此时混凝土中的最大拉应力为3.67 MPa。如图 10所示,相容性试件在经历5.53 h的低温后混凝土界面出现了较大的裂缝。
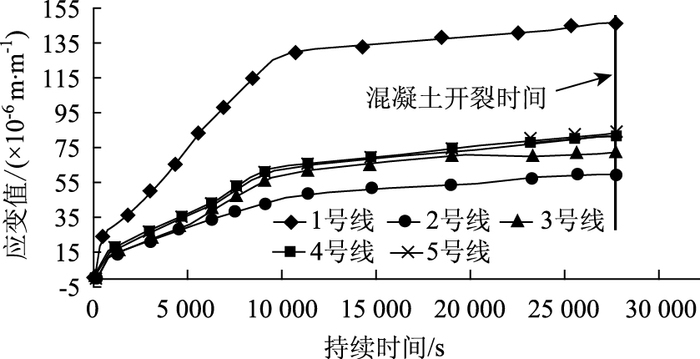
|
| 图 9 M2树脂流程4混凝土各部位应变-时间图 Fig. 9 Strain-time curves of concrete for epoxy resin M2 under process 4 |
| |

|
| 图 10 相容性试验-混凝土开裂图片 Fig. 10 Cracks in concrete after compatibility test |
| |
4 理论计算分析 4.1 模型建立
按前述试验试件尺寸建立有限元实体模型,环氧树脂与混凝土共节点连接,考虑降温40 ℃,固化收缩率以等效降温收缩代替。收缩应力σs由于其参数无法确定,不进行理论与模型的计算,以测试结果为准。后固化应力σpc过程中涉及参数较多,且很难定量测试,也不进行理论与模型的计算,以测试结果为准。以下其他参数取值为试验温度范围下测试的平均值(参考Dong UK Choi研究取μ1=0.24):
4.1.1 M1环氧树脂(1) σcu参数:
Tu=23 ℃, Tcu=50 ℃, α1=9×10-5 (m·m-1)/℃, α2=0.9×10-5 (m·m-1)/℃, E=30 MPa。
(2) σpc参数:
Tu=23 ℃, Tl=10 ℃, Th=12 ℃, Tht=100 ℃, α1=9×10-5(m·m-1)/℃, α2=0.9×10-5 (m·m-1)/℃, El=30 MPa, Eh=35 MPa, Esf=0 MPa。
(3) σtm参数:
Tch=-20 ℃, Tu=23 ℃, α1=9×10-5 (m·m-1)/℃, α2=0.9×10-5 (m·m-1)/℃, E=500 MPa。
4.1.2 M2环氧树脂(1) σcu参数:
Tu=23 ℃, Tcu=50 ℃, α1=6×10-5 (m·m-1)/℃, α2=0.9×10-5 (m·m-1)/℃, E=2 800 MPa。
(2) σpc参数:
Tu=23 ℃, Tl=58 ℃, Th=80 ℃, Tht=100 ℃, α1=6×10-5 (m·m-1)/℃, α2=0.9×10-5 (m·m-1)/℃, El=2 800 MPa, Eh=2 950 MPa, Esf=50 MPa。
(3) σtm参数:
Tch=-20 ℃, Tu=23 ℃, α1=6×10-5 (m·m-1)/℃, α2=0.9×10-5 (m·m-1)/℃, E=2 800 MPa。
4.1.3 混凝土参数E2=25 126 MPa, α2=9×10-6 (m·m-1)/℃, μ1=0.2。
4.2 计算结果试验过程中以混凝土破坏为主,即混凝土最大拉应力σz(往往出现在边角处)超过了混凝土的极限抗拉应力,设σz=βσx,β为与环氧树脂弹性模量相关的常数(线胀系数的变化对其影响很小),其取值如图 11所示(仅适用于文中的混凝土)。
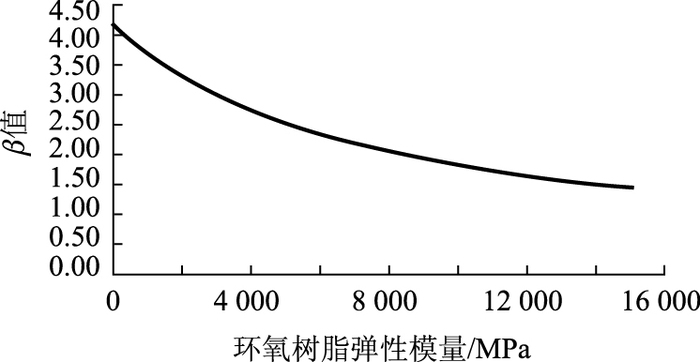
|
| 图 11 β与环氧树脂弹性模量的关系 Fig. 11 Relationship between β and elastic modulus of epoxy resin |
| |
图 12红线为混凝土中最大拉应力区域,从图中可以看出,混凝土中拉应力在σz边角处急剧变大,在混凝土与环氧树脂界面处的拉应力达到最大值,而在往中心移动时则较为平缓。这主要是因为混凝土约束了环氧树脂的收缩变形,从而造成在界面处产生了剪力,而边角处因叠合效应,出现了最大剪应力。在该剪应力的作用下,界面处混凝土出现了最大拉应力,这也与相容性试验结果相吻合。

|
| 图 12 混凝土中最大拉应力区域 Fig. 12 Maximum tensile stress zone in concrete |
| |
公式、模型计算的结果与试验结果如表 4、表 5所示。从结果中可以看出,理论计算与有限元分析的结果吻合度较好;而与试验结果σz相差较大,这主要是混凝土在测试过程中开裂造成的,混凝土的极限抗拉强度为4~5 MPa左右,超过该应力混凝土即会开裂,但采用理论和有限元结果能有效预测开裂情况。
| 编号 | 测试应力类型 | 试验结果 | 理论结果 | 有限元结果 | |||
| σx | σz | σz | σx | σz | σx | σz | |
| 1 | σs | σs, z | — | — | — | — | — |
| 2 | σcu | σcu, z | — | 0.09 | 0.37 | 0.05 | 0.37 |
| 3 | σpc | σpc, z | — | — | — | — | — |
| 4 | σtm | σtm, z | 4.27 | 2.45 | 9.51 | 2.44 | 9.47 |
| 编号 | 测试应力类型 | 试验结果 | 理论结果 | 有限元结果 | |||
| σx | σz | σz | σx | σz | σx | σz | |
| 1 | σs | σs, z | 0.69 | — | — | — | — |
| 2 | σcu | σcu, z | 3.76 | 5.07 | 15.36 | 5.01 | 15.18 |
| 3 | σpc | σpc, z | 0.38 | — | — | — | — |
| 4 | σtm | σtm, z | 4.12 | 6.57 | 19.91 | 6.42 | 19.45 |
5 结论
(1) 从环氧树脂浇注到混凝土上那一刻开始,就会由于树脂的固化反应、以及温度的变化而在体系内部产生应力,主要包含收缩应力、固化应力、后固化应力、温度应力。
(2) 较小的弹性模量能有效降低环氧树脂-混凝土叠合结构的固化应力、后固化应力和温度应力,但常温下表现为低弹性模量的环氧树脂在低温时其弹性模量会急剧上升,有时会增加几十倍,大大增加了低温时的温度应力。
(3) 常温养护时,高温后固化的环氧树脂-混凝土叠合结构的内应力变化比较复杂,因高温后固化会降低环氧树脂的线性热膨胀系数,增加其弹性模量以及热变形温度,同时也会产生固化收缩,最终应力累积的计算需要大量试验数据作为支撑。
(4) 通过分析和推导,依据ASTM C884试验方法,可以计算出该方法下混凝土不开裂所要求的最大环氧树脂的弹性模量。如:取σz=2.5 MPa,考虑降温40 ℃时,取β=4,则能通过该试验的环氧树脂最大平均弹性模量为131.9 MPa(20 ℃至-20 ℃的平均弹性模量,环氧树脂线胀系数取100×10-6 (m·m-1)/℃)。
(本文计算仅适用于不掺加填料的环氧树脂-混凝土叠合结构,不适用于环氧砂浆-混凝土结构。)
| [1] |
WILSON D L, HENLEY E H. Thin Polymer Bridge Deck Overlays:WSDOT's Ten Year Evaluation[R]. Washington, D. C.:Bridge and Structures Office, 1995.
|
| [2] |
EDWARD M P. Epoxy Adhesive Formulations[M]. America: McGraw-Hill Chemical Engineering, 2005.
|
| [3] |
ACI 209R-1992, Prediction of Creep, Shrinkage, and Temperature Effects in Concrete Structures[S].
|
| [4] |
YUAN Z F, YIN H M. Elastic Thermal Stresses in a Circular Overlay/Rigid Substrate System[J]. Mechanics Research Communications, 2011, 38(4): 283-287. |
| [5] |
SPRINKEL M M. Long-term Performance of Polymer Concrete for Bridge Decks[R]. Washington, D.C.:Transportation Research Board, 2011.
|
| [6] |
DAVID W, FOWLER D W. State of the Art in Concrete Polymer Materials in the U.S.[R]. East Aurora:The University of Texas at Austin, 1997.
|
| [7] |
CHOI D, FOWLER D W, WHEAT D L. Thermal Stresses in Polymer Concrete Overlays[R]. Farmington Hills:American Concrete Institute, 1996:93-122.
|
| [8] |
NEGHEIMISH A I. Bond Strength, Long Term Performance and Temperature Induced Stresses in Polymer Concrete-Portland Cement Concrete Composite Members[D]. Austin:University of Texas at Austin, 1988.
|
| [9] |
ZHANG Neng-hui. Thermoelastic Stresses in Multilayered Beams[J]. Thin Solid Films, 2007, 515(23): 8402-8406. |
| [10] |
ACI 503R-1993, Use of Epoxy Compounds with Concrete[S].
|
| [11] |
HUTCHINSON J W. Stresses and Failure Modes in Thin Films and Multilayers[D]. Cambridge:Harvard University, 1996. https://www.mendeley.com/research-papers/stresses-failure-modes-thin-films-multilayers/
|
| [12] |
HUTCHINSON J W, SUO Z. Mixed Mode Cracking in Layered Materials[J]. Advances in Applied Mechanics, 1991, 29(8): 63-191. |
| [13] |
SPRINKEL M M. Polymer Concretes:Adhesives and Sealers[R]. Washington, D.C.:National Research Council, 2000.
|
| [14] |
NISHIMURA T, NAKAGAWA Y. Analysis of Stress due to Shrinkage in a Hardening Process of Liquid Epoxy Resin[J]. Heat Transfer-Asian Research, 2002, 31(3): 194-211. |
| [15] |
陈平, 王德中. 环氧树脂及其应用[M]. 北京: 化学工业出版社, 2004. CHEN Ping, WANG De-zhong. Epoxy Resin and Its Applications[M]. Beijing: Chemical Industry Press, 2004. |
| [16] |
RAMSAMOOJ D V. An Innovative Technique for Using Polymer Composites in Airport Pavement Rehabilitation[J]. Composites Part B:Engineering, 2001, 32(1): 57-66. |
| [17] |
ASTM C884-2010, Standard Test Method for Thermal Compatibility between Concrete and Epoxy Resin Overlay[S].
|
| [18] |
ASTM E251-2014, Standard Test Method for Performance Characteristics of Metallic Bonded Resistance Strain Gages[S].
|
 2017, Vol. 34
2017, Vol. 34
