扩展功能
文章信息
- 赵少杰, 任伟新
- ZHAO Shao-jie, REN Wei-xin
- 基于WIM数据和断裂力学方法的钢桥疲劳强度评估
- Evaluation of Fatigue Strength of Steel Bridge Based on WIM Data and Fracture Mechanics Method
- 公路交通科技, 2017, 34(12): 37-43
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 37-43
- 10.3969/j.issn.1002-0268.2017.12.006
-
文章历史
- 收稿日期: 2016-12-09
2. 湖南省交通规划勘察设计院, 湖南 长沙 410008;
3. 合肥工业大学 土木与水利工程学院, 安徽 合肥 230009
2. Hunan Provincial Communications Planning, Survey & Design Institute, Changsha Hunan 410008, China;
3. School of Civil Engineering, Hefei University of Technology, Hefei Anhui 230009, China
近年来,桥梁断裂垮塌事故频发,很多是桥梁在重车荷载作用下发生了疲劳断裂所致。疲劳断裂作为桥梁结构最常见的破坏形式,是钢桥在设计、施工及运营管养中需要特别注意的问题。大型钢结构桥梁因其焊接节点的构造和受力均较复杂,目前钢桥设计规范对其疲劳强度并没有明确规定。基于S-N曲线的名义应力法和热点应力法等常规疲劳强度评估方法均存在较大的局限,如均忽略了材料的初始缺陷、复杂结构的名义应力较难定义、疲劳裂纹的扩展阶段无法描述等[1-2],故工程中常需要借助疲劳试验对钢桥结构的疲劳强度进行验证,既费时也费力,而断裂力学方法在结构疲劳强度评估方面具有先天优势。断裂力学假定材料存在初始缺陷,注重研究含缺陷材料在外界荷载作用下裂纹的扩展开裂等规律,结合现代无损探伤及长期监测技术,能够克服传统强度理论的局限,近年来逐渐得到了重视和应用。王春生等[3]提出了基于钢筋S-N曲线和断裂力学模型的既有混凝土桥梁剩余寿命评估方法。郑淳[4]从概率断裂力学的角度研究了公路钢桥疲劳寿命预测及可靠度计算方法。邓扬等[5]基于健康监测数据对钢箱梁顶U肋焊接细节的疲劳断裂可靠性进行了分析等。上述研究多基于理想断裂力学模型,缺乏对具体构造细节的选取和其应力强度因子的计算,而疲劳强度断裂力学评估方法的难点在于准确地获得构造细节的应力强度因子[6]。本研究基于断裂力学理论,采用现代有限元计算和理论分析等多种方法,获得了典型构造细节的应力强度因子式,以此为依据采用裂纹扩展理论反算得到结构的疲劳强度,并与试验值和规范值进行了比较分析。通过工程实例及试验,结合桥梁动态称重(WIM)系统监测数据,进一步验证该断裂力学方法在钢桥疲劳强度评估方面的适用性和准确性。
1 钢桥疲劳强度的断裂力学分析方法 1.1 应力强度因子及K判据应力强度因子是断裂力学的基本概念之一。断裂力学研究在Irwin提出应力强度因子概念后才获得重大突破并快速发展起来[7]。断裂力学假设材料中存在初始裂纹,并分为3种类型:张开型(Ⅰ型)、滑移型(Ⅱ型)、撕裂型(Ⅲ型)。其中Ⅰ型裂纹对结构受力最不利,易引起结构断裂破坏,是本研究的重点研究对象。应力强度因子定义为:
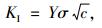
|
(1) |
式中,Y为裂纹形状修正因子,与结构受力、裂纹类型及位置等有关;σ为工作应力;c为裂纹尺寸。
结构不发生低应力断裂的K判据定义为:
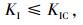
|
(2) |
式中KIC为临界应力强度因子即断裂韧性,可通过试验测定。
1.2 断裂力学判据的适用范围K判据适用于材料的低应力脆性破坏,要求构件工作应力不能太大,裂纹尺寸和材料屈服强度不能太小,一般要求临界断裂应力σc<0.63σs(σs为材料屈服强度)。对于工程上出现的微小裂纹,一般用弹塑性断裂力学来分析。但对高周疲劳,在远低于屈服应力的疲劳荷载作用下,构件整体的力学响应是线性的,裂纹的扩展仍可采用线弹性断裂力学的K判据进行。事实上大量试验也证实了这一点[8],疲劳裂纹扩展速率dc/dN与应力强度因子的幅值ΔK存在如下函数关系:
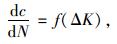
|
(3) |
式中N为应力循环次数。
1.3 焊接钢桥典型构造细节的应力强度因子计算焊接钢桥的构造细节很多,本研究重点分析角焊缝和对接焊缝中有代表性的两种典型焊接构造细节,即角接头棱角焊缝和T形接头对接焊缝构造细节。分别采用有限元方法和解析的G*积分法对其应力强度因子进行计算,并以此作为评估结构构造细节疲劳强度的依据。其他构造细节可以采用类似方法处理。本研究裂纹考虑为Ⅰ型裂纹,因为Ⅰ型裂纹是低应力断裂的主要原因,是最危险的情况。材料统一取14MnNbq钢材,屈服强度为370 MPa,弹性模量为2.1×105MPa,泊松比为0.3。
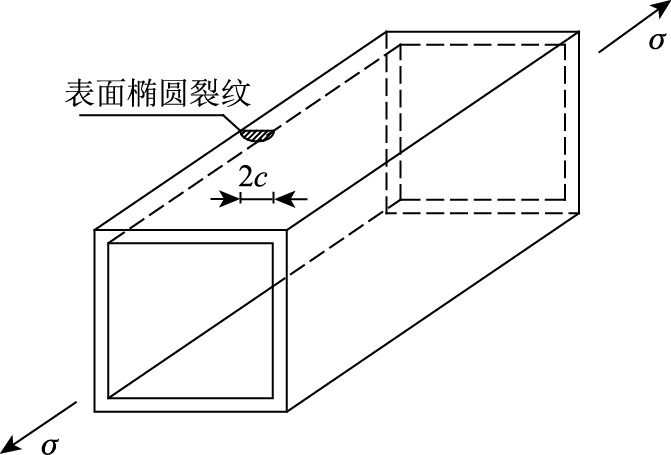
考虑箱形弦杆棱角焊缝中存在垂直拉力方向的表面半椭圆裂纹,结构简化成空间箱形弦杆,结构受力及裂纹位置示意如图 1所示。一般裂纹位置需要由实际探伤决定,对于未探伤或探伤未发现裂纹的构件,假设裂纹出现在焊缝区。因一般箱形弦杆在4个角点处应力最大,而棱角焊缝及裂纹也正位于该处,符合裂纹出现位置最不利原则。假设计算模型的半椭圆裂纹尺寸为c, 采用有限元方法计算不同的裂纹尺寸c下的应力强度因子,并拟合获得相应的应力强度因子表达式。
|
| 图 1 棱角焊缝裂纹位置及受力示意图 Fig. 1 Schematic diagram of crack location and force in arris weld |
| |
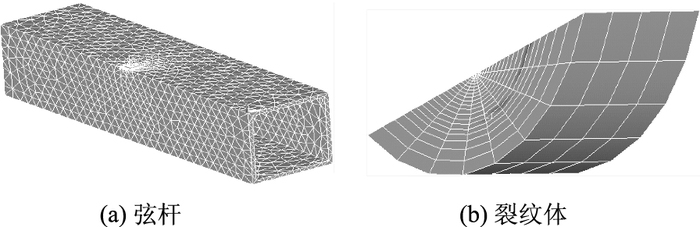
采用由垂直于裂纹前沿线的平面单元先沿裂纹前沿自动生成二维奇异单元,然后采用体扫略划分网格方式来生成三维奇异单元[9],生成的三维模型及裂纹局部见图 2。由此模型可计算出相应的应力强度因子。
|
| 图 2 弦杆有限元模型及裂纹体网格划分 Fig. 2 Finite element model of chord and cracked body meshing |
| |
由1.1节知,K值的变化取决于Y值的变化,研究表明Y值主要与裂纹半长c有关[10],故可将Y值表达成c的函数。取c为参数,计算不同c下的K值,然后采用最小二乘法拟合,获得形状修正因子Y值与裂纹半长c的变化关系,最后得到K值的表达式如下:
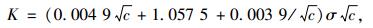
|
(4) |
式中,c≠0;拟合相关系数为0.99。
(2) T形接头对接焊缝构造细节
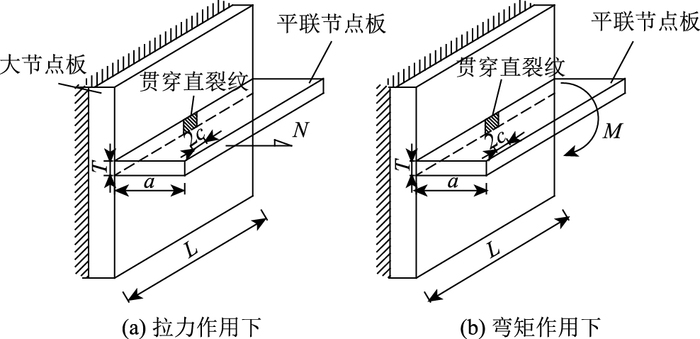
考虑裂纹出现在T形接头板间焊接的焊缝中部,如图 3所示,为贯穿直裂纹情况。根据裂纹边界非自发扩展能量释放率的概念,假设把贯穿直裂纹看成由椭圆孔当其短半轴趋向于0时退化而成,运用G*积分守恒性计算其应力强度因子。计算获得的K值表达式为:
|
| 图 3 T形接头对接焊缝中裂纹位置及受力示意图 Fig. 3 Schematic diagram of crack location and force in butt weld of T-joint |
| |
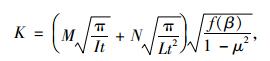
|
(5) |
式中,M为端截面弯矩;I为板截面抗弯惯矩;t为板件厚度;N为板端拉力;L为平联板宽度;μ为材料的泊松比;β=c/L。
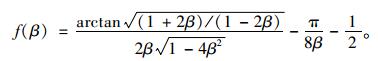
|
(6) |
由Paris公式,
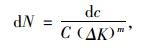
|
(7) |
即有:
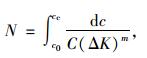
|
(8) |
式中,m为疲劳强度曲线常数,与材料有关;C为与材料等因素有关的系数, 对于无试验资料的桥梁结构钢[11],可取C=(1.315×10-4)/895.43; cc为临界断裂裂纹尺寸;c0为初始裂纹尺寸。
断裂韧性KIC参考文献[12]取59.5 MPa。KIC中对应的σ为实际构件断裂时的最大工作应力。对于桥梁用钢,其基本弯曲和轴向容许应力约为其屈服强度的0.6倍,而一般主梁设计应力控制在容许应力的0.8~0.95倍[13],故实际最大工作应力为(0.48~0.57)σs。在文中统一取σc=0.5σs,满足小范围屈服的控制条件σc<0.63σs的假定。由前面获得的应力强度因子计算式,反算cc为84.9 mm。c0一般根据无损探伤确定,当无裂纹时,可假定为焊件中无损探伤灵敏度的下限值,参考文献[14]取2.5 mm。根据式(1),结合上述参数采用数值积分方法,计算得:
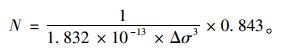
|
(9) |
对应等效200万次疲劳强度,令上式等于2.0×106,可得容许等效应力幅:
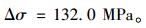
|
为了与试验结果及规范值有一定的对比性,T形接头的平联板宽度L取200 mm,板厚t取10 mm,将式(5)变换后有:
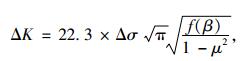
|
(10) |
式中,Δσ为工作应力幅值;σc,c0,KIC取值同前,计算临界断裂裂纹尺寸cc=71.5 mm,代入Paris公式,同理运用数值积分后并令N=2.0×106,得:
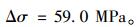
|
上述各构造细节疲劳强度计算结果,其相应的等效200万次疲劳强度(容许应力幅)的国外规范值[15-18]、试验值[19-20]的对比分析见表 1。
| 规范名称 | 等效200万次疲劳强度 (容许应力幅)/MPa | 备注 | |
| ①角接头 棱角焊缝 | ②T形接头 对接焊缝 | ||
| 英国规范(BS) | 91 | 50 | 取值范围在这两者之间。 |
| 124 | 68 | ||
| 日本钢结构规范 (JSSC) | 125 | 65 | 构造①对应规范构造细节C级;构造②对应规范构造细节F级。 |
| 欧洲钢结构规范 (ECCS) | 112 | 50 | 构造①单侧施焊;构造②对应无圆弧过渡的纵向附连件长L>100 mm的情况。 |
| 美国规范(AREA) | 102 | 56 | 构造①对应规范构造细节B级;构造②端部不磨修。 |
| 铁科院疲劳试验结果 | 120 | 71 | 构造①为V形坡口不熔透纵向角焊缝正应力疲劳试验;构造②为平联节点板焊在Ⅰ形梁腹板上的疲劳试验,端部打磨。 |
| 芜湖大桥疲劳试验结果 | 122 | 73 | 构造①为角焊缝正应力疲劳试验;构造②为端部打磨情况, 为试验推荐值。 |
| 本研究方法计算结果 | 132 | 59 | |
对比可见,采用断裂力学方法计算获得的等效200万次的疲劳强度值与规范值及试验值均吻合良好,特别是角接头棱角焊缝构造细节的偏差值基本在10%内,计算精度是令人满意的。其中T形接头对接焊缝细节的偏差稍大,但也在20%以内。引起偏差的主要原因有:规范值及试验值采用的构造细节与本研究计算模型之间的差异、初始裂纹形状尺寸及位置的假设误差、参数C和m的取值误差、焊接残余应力的影响等。
对比上述两种构造细节的疲劳强度可知,T形接头构造细节的疲劳强度远低于棱角焊缝正应力构造细节的疲劳强度,故在设计和施工时应特别注意T形接头构造。
2 基于WIM系统数据和的断裂力学方法的钢桥疲劳强度评估工程实例 2.1 桥梁概况镇胜高速公路坝陵河大桥为主跨1 088 m的简支钢桁加劲梁悬索桥,桥跨布置为(248+1 088+228)m。加劲梁采用钢桁梁结构,桁高为10 m,标准节间长为10.8 m。上弦杆、下弦杆及斜腹杆均选用闭口箱形断面,双向四车道。大桥在修建时安装了长期健康监测系统,以实时了解桥梁的健康运营状况,其中在桥面安装了荷载动态称重系统,如图 4所示。坝陵河大桥钢桁加劲梁采用焊接整体节点,节点外拼接,在修建时该技术在国内首次在悬索桥钢桁梁中应用。由于整体节点板材之间采用焊接连接,故节点的焊接强度, 特别是疲劳可靠性,是工程重点关注的问题。本节针对钢桁梁节点构造的疲劳强度展开实例研究。

|
| 图 4 坝陵河大桥及其桥面WIM系统 Fig. 4 Baling River Bridge and WIM system in bridge deck |
| |
2.2 钢桁梁节点构造的疲劳强度评估 2.2.1 基于WIM系统监测数据的等效应力幅值计算
为了更准确地对焊接钢桥的疲劳强度进行评估,通过桥梁健康监测系统采集的数据,分析获取受力关键构件的应力幅,并结合断裂力学方法进行疲劳评估。如果桥梁在结构关键受力部位安装了应力传感器,则可以通过长期实测数据直接对该结构进行疲劳强度评估计算。如果桥梁安装了实时WIM系统,则可通过实测交通荷载数据,结合全桥有限元仿真计算分析,间接获取结构的等效应力幅。坝陵河大桥节点构造的疲劳强度评估采用后一种方法。
(1) 实际交通量统计
表 2给出了坝陵河大桥WIM系统实测1个月的车辆荷载通行情况。
| 车重/kN | <30 | 30~200 | 200~400 | 400~550 | >550 | 总数 | 日平均 交通量 |
| 数量/veh | 361 774 | 70 234 | 29 741 | 22 080 | 4 800 | 488 629 | 15 763 |
| 百分比/% | 74.0 | 14.4 | 6.1 | 4.5 | 1.0 | 100.0 | 3.2 |
从表 2可见,日平均双向通行车辆为15 763 veh,其中超过30 kN的车辆荷载数量约占总数的26%。
(2) 等效200万次疲劳内力幅和应力幅
英国BS5400、美国AASHTO等规范均规定对于轴重较小的小型车(一般取车重小于30 kN),在计算疲劳损伤时可以忽略不计。由表 2数据可知,能引起桥梁疲劳损伤的日平均单向货车交通量为:
ADTT=0.5×15 763×0.26=2 050 veh/d。
由此按照AASHTO规范可计算设计寿命100 a内单车道的交通车辆数ADTTsl及内力循环次数N:
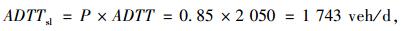
|
(11) |
N=1 743×365×100=63, 619, 500次,式中P为单车道系数,按规范取值0.85。
按照Miner线形疲劳累积损伤理论,结合坝陵河大桥WIM系统实测数据,可计算得到实际交通的等效疲劳车重:
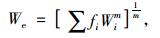
|
(12) |
式中, Wi为第i种产生疲劳影响的实测车辆重量;fi为Wi在所有产生疲劳影响的车辆总数目中所占的比例;m为疲劳强度曲线参数。
然后通过在桥梁上加载获得上弦杆的等效内力幅,结合上述单车道内力循环次数,运用疲劳累积损伤等效原则,即考虑变幅与常幅内力幅之间的关系,可求出坝陵河大桥节点杆件等效200万次疲劳内力幅。其中变幅与常幅内力幅之间的换算关系与式(9)类似,即式中Wi为第i个变幅内力幅,fi为第i个内力幅作用次数占总内力幅作用次数的比例,则We即为等效内力幅。计算获得的上弦杆等效200万次疲劳内力幅为3 422 kN,换算得等效应力幅值Δσ为45.5 MPa。
2.2.2 节点构造的疲劳强度评估钢桁梁节点构造的弦杆主要承受轴力,其弦杆的角接头棱角焊缝为主要承受疲劳荷载的受力焊缝,故疲劳评估针对弦杆的角接头棱角焊缝构造进行。钢桁梁材料为Q345D钢材,参考文献[8], KIC取50 MPa,屈服强度σs为325 MPa,取构件临界断裂应力σc=0.5σs。由式(2)反算临界断裂裂纹尺寸cc为80.0 mm。节点构造经探伤未发现裂纹,故同上节假定焊件中初始裂纹尺寸为2.5 mm。由(4)式可得:
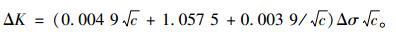
|
(13) |
根据上节取C=1.832×10-13,m=3,由式(8)结合上式及相关参数计算得:
N=4.88×107>2.0×106。
可见,断裂力学计算结果显示该焊接节点构造疲劳强度满足设计要求,节点构造具有足够的疲劳寿命。
2.3 节点构造疲劳强度的模型试验验证为了验证坝陵河大桥钢桁梁节点构造的实际疲劳强度是否与断裂力学的评估结论一致,选择受力最不利的钢桁梁上弦杆吊点节点连接构造(以下简称节点构造)进行疲劳模型试验验证。该节点将承受的恒载及桥面活载通过吊杆传递到主缆,根据实桥结构按1:1的比例设计了钢桁梁节点模型,以尽可能地反映实桥结构的受力特性及连接构造细节。
试验模型共包括:节点模型试件、加载分配梁及连接梁、加载支墩、支墩横梁等部分。试验模型在顺桥向长3.42 m,包含整个节点构造细节,主要有以下几种:(1)弦杆角接头棱角焊缝构造细节;(2)T形接头角焊缝构造细节;(3)箱形弦杆与横隔板交叉焊缝构造细节。其中第1种构造细节为主要承力焊缝细节。对该节点模型在MTS疲劳试验机上进行常幅200万次疲劳试验加载,以验证该节点构造的疲劳强度情况。为了加载方便,节点模型疲劳试验采用杠杆原理进行加载。试验时将模型倒转,使节点耳板朝下,通过耳板连接梁把试件和加载分配梁连起来。试验模型及加载布置图如图 5所示。

|
| 图 5 疲劳试验模型及加载布置 Fig. 5 Fatigue test model and loading arrangement |
| |
试验结果:整个疲劳加载过程模型试件未发现异常现象,试件工作正常。每次停机静载试验后,检查模型试件及其焊缝,均未发现裂纹。200万次疲劳试验后,对模型试件进行检查,未发现裂纹。继续加载至240万次,检查模型试件及焊缝,仍未发现裂纹。故说明该节点构造的疲劳强度满足设计要求。
由2.2节断裂力学的理论分析知,该节点构造的疲劳强度也满足设计要求。故试验结果和断裂力学的理论评估结论一致,这也从侧面证明了2.2节的断裂力学评估结论和相应应力强度因子计算结果的正确性。
3 结论基于断裂力学方法,对焊接钢结构桥梁的几种典型构造细节进行了应力强度因子计算,并以此为基础评估了焊接钢桥结构的疲劳强度。主要结论有:
(1) 采用有限元及G*积分法获得了焊接钢桥角接头棱角焊缝和T形接头对接焊缝构造细节典型受力状态的应力强度因子表达式。
(2) 由应力强度因子计算获得的等效200万次疲劳强度结果与各国规范值、试验值均吻合良好,特别是棱角焊缝构造细节的计算误差基本在10%以内,说明了应力强度因子计算和疲劳强度评估结果的准确性。
(3) 工程实例及疲劳模型试验也进一步表明,基于WIM系统监测数据和断裂力学方法的钢桥结构疲劳强度评估方法力学判据明晰,评估结论可靠。
当然,该方法在桥梁疲劳强度评估方面还面临一些挑战,其评估的准确性和有效性还依赖很多相关因素,如初始裂纹大小及分布假设的合理性、各构造细节应力强度因子计算的准确性、相关材料参数测定的准确性、疲劳荷载数据统计的充分代表性等。但可以预见,随着结构无损探伤和桥梁健康监测等技术的发展及断裂力学研究的不断深入,基于断裂力学理论和长期健康监测数据的桥梁结构强度评估方法将会得到不断的发展和广泛的应用。
| [1] |
何东升, 肖海珠, 张晓勇. 公路正交异性钢桥面板细节疲劳研究[J]. 公路交通科技, 2016, 33(1): 77-81. HE Dong-sheng, XIAO Hai-zhu, ZHANG Xiao-yong. Research on Detail Fatigue of Orthotropic Steel Deck in Highway Bridge[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 77-81. |
| [2] |
NOROOZI A H, GLINKA G, LAMBERT S. Prediction of Fatigue Crack Growth under Constant Amplitude Loading and a Single Overload Based on Elasto-plastic Crack Tip Stresses and Strains[J]. Engineering Fracture Mechanics, 2008, 75(2): 188-206. |
| [3] |
王春生, 周江, 吴全友, 等. 既有混凝土桥梁疲劳寿命与使用安全评估[J]. 中国公路学报, 2012, 25(6): 101-107. WANG Chun-sheng, ZHOU Jiang, WU Quan-you, et al. Fatigue Life and Service Safety Assessment for Existing Concrete Bridges[J]. China Journal of Highway and Transport, 2012, 25(6): 101-107. |
| [4] |
郑淳. 基于断裂力学的公路钢桥疲劳寿命可靠度方法研究[D]. 广州: 华南理工大学, 2013. ZHENG Chun. Research on Fatigue Life Reliability Evaluation of Highway Steel Bridges Based on Fracture Mechanics[D]. Guangzhou:South China University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10561-1014153497.htm |
| [5] |
邓扬, 丁幼亮, 李爱群, 等. 钢箱梁桥焊接细节的疲劳断裂可靠性分析[J]. 工程力学, 2012, 29(10): 122-127. DENG Yang, DING You-liang, LI Ai-qun, et al. Fracture Fatigue Reliability of Welded Details in Bridge Steel Box Girders[J]. Engineering Mechanics, 2012, 29(10): 12-127. |
| [6] |
POPA C O, HARAGÂŞ S. Some Considerations about the Influence of the Stress Intensity Factors KImin, KⅡmax and Keq in Fatigue Crack Propagation in the Substrate of the Gear Teeth[J]. Applied Mechanics and Materials, 2016, 823: 23-29. |
| [7] |
李庆芬, 胡胜海, 朱世范. 断裂力学及其工程应用[M]. 哈尔滨: 哈尔滨工程大学出版社, 2008. LI Qing-fen, HU Sheng-hai, ZHU Shi-fan. Fracture Mechanics and Engineering Application[M]. Harbin: Harbin Engineering University Press, 2008. |
| [8] |
刘宝琛. 实验断裂、损伤力学测试技术[M]. 北京: 机械工业出版社, 1994, 157-166. LIU Bao-chen. Experimental Fracture, Damage Mechanics and Testing Technology[M]. Beijing: China Machine Press, 1994, 157-166. |
| [9] |
王锋, 黄其青, 殷之平. 三维裂纹应力强度因子的有限元计算分析[J]. 航空计算技术, 2006, 36(3): 125-129. WANG Feng, HUANG Qi-qing, YIN Zhi-ping. Analysis of Emulational Limited Element Method for the Three-dimensional Stress Intensity Factors[J]. Aeronautical Computing Technique, 2006, 36(3): 125-129. |
| [10] |
孙宏才, 高磊, 徐关尧, 等. 矩形板中心裂纹有限元数值分析[J]. 解放军理工大学学报:自然科学版, 2006, 7(3): 271-275. SUN Hong-cai, GAO Lei, XU Guan-yao, et al. Finite Element Numerical Analysis in Center-cracked Rectangular Panel[J]. Journal of PLA University of Science and Technology:Natural Science Edition, 2006, 7(3): 271-275. |
| [11] |
霍立兴. 焊接结构工程强度[M]. 北京: 机械工业出版社, 1995, 270-290. HUO Li-xing. Engineering Strength of Welded Structure[M]. Beijing: China Machine Press, 1995, 270-290. |
| [12] |
李国清, 祝时召, 李建兵, 等. 14MnNbq焊接件全范围疲劳裂纹扩展性能研究[J]. 桥梁建设, 2006(4): 33-37. LI Guo-qing, ZHU Shi-zhao, LI Jian-bing, et al. Study of Full Range Fatigue Crack Growth Behavior of 14MnNbq Welds[J]. Bridge Construction, 2006(4): 33-37. |
| [13] |
吴冲. 现代钢桥(上册)[M]. 北京: 人民交通出版社, 2006, 181-190. WU Chong. Modern Steel Bridge (Volume 1)[M]. Beijing: China Communications Press, 2006, 181-190. |
| [14] |
崔洪斌, 石德新, 李晗, 等. 潜艇锥柱结合壳焊缝焊趾处初始裂纹尺寸评定[J]. 哈尔滨工程大学学报, 2006, 27(4): 492-500. CUI Hong-bin, SHI De-xin, LI Han, et al. Evaluation the Size of Initial Crack in Welding Toes of Joint of Cylinder and Cone[J]. Journal of Harbin Engineering University, 2006, 27(4): 492-500. |
| [15] |
BS5400-2-2006, Steel, Concrete and Composite Bridges-Part 2:Specification for Loads[S].
|
| [16] |
JSSC.2003, Fatigue Design Recommendations for Steel Structures[S].
|
| [17] |
EN1993-1-9:2005, Design of Steel Structures-Part 1-9:Fatigue[S].
|
| [18] |
AREMA 2007, Manual for Railway Engineering[S].
|
| [19] |
任伟平. 焊接钢桥结构细节疲劳行为分析及寿命评估[D]. 成都: 西南交通大学, 2009: 90-105. REN Wei-ping. Fatigue Behaviour Analysis and Fatigue Life Evaluation of Structural Details in Welded Steel Girder Bridges[D]. Chengdu:Southwest Jiaotong University, 2009:90-105. http://d.wanfangdata.com.cn/Thesis/Y1430694 |
| [20] |
张玉玲, 潘际炎, 张建民, 等. 芜湖长江大桥钢梁细节疲劳强度的研究[J]. 中国铁道科学, 2001, 22(5): 15-21. ZHANG Yu-ling, PAN Ji-yan, ZHANG Jian-min, et al. Research on Fatigue Strength for Steel Girder Details of Wuhu Yangtze River Bridge[J]. China Railway Science, 2001, 22(5): 15-21. |
 2017, Vol. 34
2017, Vol. 34
