扩展功能
文章信息
- 李明睿
- LI Ming-rui
- 车道宽度以弧长定义的高速环道横断面设计研究
- Study on High-speed Track Section Design in which Lane Width Defined as Curve Length
- 公路交通科技, 2017, 34(12): 30-36
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 30-36
- 10.3969/j.issn.1002-0268.2017.12.005
-
文章历史
- 收稿日期: 2017-01-19
汽车试验场高速环道(以下简称“高环”)的横断面设计是其几何设计中最重要的组成部分。区别于一般公路横断面,高环因其设计平衡车速高、各车道设计车速差异大而在平曲线段采用曲线形式的横断面[1]。
传统的高环横断面设计理论中,设计车道宽均定义为车道的水平投影宽度[2-3]。国内几乎所有已建成高环的几何设计均以此为理论基础,如一汽海南试验场、通用广德试验场、长城汽车徐水试验场等。过去国内仅有上海大众安亭试验场的高环(国外单位设计)采用车道宽度以路面弦长定义进行设计[4]。国内学者对高环横断面设计的研究主要着重在横断面不同的方程形式选择与比较,而没有对车道宽度的定义方式进行过适用性分析或相关研究。
近年随着试验车辆性能的提升,对高环的设计车速要求逐渐提高,设计横断面规模也在逐渐变大。由于高环横断面为曲线形式,当设计车道数较多时,车行道断面宽度分别按投影宽定义与按行驶路面的曲线弧长定义时,在横断面设计中会体现出较大差异。因此有必要对两者进行对比分析研究。
1 不同车道宽度定义下横断面设计的异同 1.1 车道宽度定义为投影宽或曲线弧长的区别传统的高环横断面设计时,车道宽度的定义与普通公路设计时是一致的,即采用水平投影宽度。根据《公路路线设计规范》(JTG D20—2006)[5],宽度取值与设计车速相关,通常为3.0~3.75 m。在公路设计中,即使有8%的超高,其路面斜长与其水平投影宽相差无几。例如当车道宽取3.75 m时,其实际斜长3.762 m,相差仅1.2 cm。
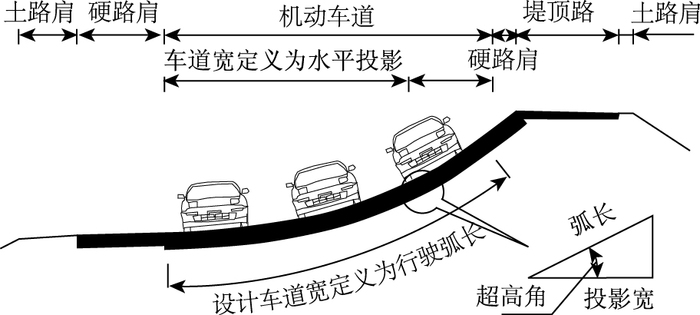
但是这种情况在高环平曲线段的横断面设计中有所不同。特别是当设计车速高而采用较大的超高时,其水平投影宽与实际路面弧长就会有较大差距。这两种不同宽度定义的含义如图 1所示。可做简单估算,当横断面某个车道超高角为40°或以上时(大型高环常见超高角度),按传统设计方法,设计车道宽度水平投影取3.75 m,则其实际行驶面弧长约为4.9 m,两者相差30.67%。而实际行驶路面宽度4.9 m显得过于富余。
|
| 图 1 不同车道宽度定义的示意图 Fig. 1 Schematic diagram of different lane width definitions |
| |
如果同时考虑高环的设计车速高,最大超高角大,横断面车道数较多时(各车道宽度富余累加),整个设计横断面的水平投影宽与实际行驶面曲线弧长就会有较大差异。
因此对于横断面规模较大的高环设计,车道宽度以实际行驶面弧长来定义,从设计理念上看显得更有依据并且经济合理。
1.2 横断面基本设计原理在高环平曲线段的横断面设计中,其基本原则是各车道设计中线处的超高角、半径、控制车速满足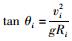
车道宽度无论用哪种方式定义,横断面无论采用哪种曲线形式,上述基本设计原理是一致的。根据不同设计的着重点和相关条件,横断面曲线形式通常可采用高次抛物线、对数曲线、复合函数曲线等。在国内大部分工程实践中,考虑横断面速度分布过渡更接近线性及计算的便捷性,通常采用三次抛物线作为横断面设计的方程形式。因此文中以三次抛物线横断面为例, 说明不同车道宽度定义下横断面的具体计算求解方法,据此可类推至其他曲线方程形式的横断面计算求解。
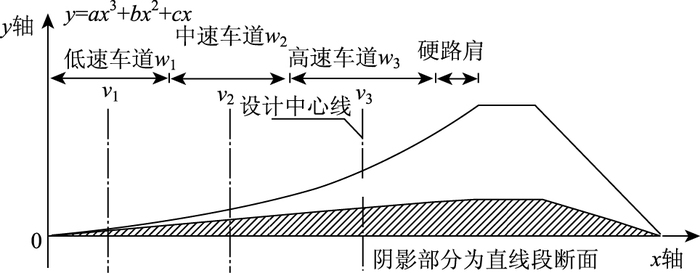
对于设计车道宽度以水平投影宽定义时,即传统的高环横断面设计模型如图 2所示(以三车道抛物线形式横断面为例):
|
| 图 2 车道宽以水平投影宽定义时的计算模型图 Fig. 2 Calculation model diagram when defining lane width as horizontal projective width |
| |
对于平曲线段任意一个横断面,设抛物线方程为:y=ax3+bx2+cx,对于各个车道中线位置有: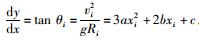
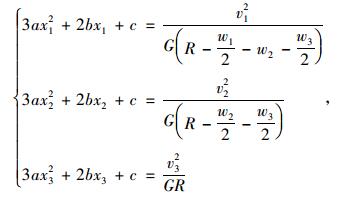
|
(1) |
式中,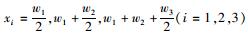
上述方程组中仅含a,b,c这3个未知数,可通过Cramer法则求解上述线性方程,得到三次抛物线方程系数的解,然后根据平曲线段上各位置曲率半径逐个确定每处对应的横断面抛物线方程式。
2 车道宽以弧长定义的横断面设计方法 2.1 设计计算模型与方法车道宽度以弧长定义设计时,方程组(1)中采用的车道宽度Wi应为实际行驶路面的弧长。相应的各车道中线对应的平曲线半径Ri的计算需要先求得以车道宽为弧长定义时各车道对应的水平投影宽度,进而求得各车道中线对应的平曲线曲率半径。设计车道宽度以行驶路面弧长定义时,其设计模型如图 3所示(以三车道抛物线形式横断面为例):
|
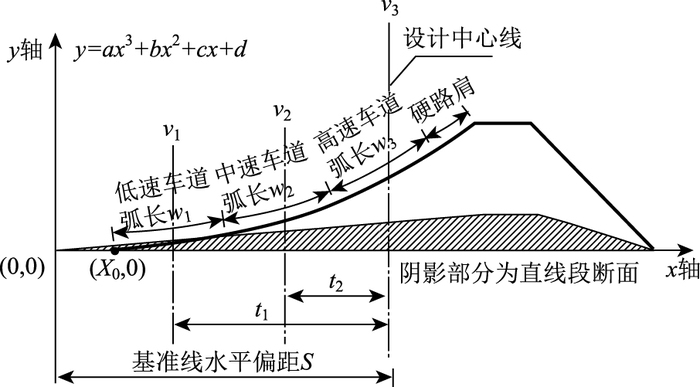
| 图 3 车道宽以弧长定义时的计算模型图 Fig. 3 Calculation model diagram when defining lane width as curve length |
| |
设直缓点处横断面(图中阴影断面)车道边线起点位于坐标系的原点,y轴为设计基准轴与设计中心线(通常为高速车道中线)的水平偏距为S。在缓和曲线段横断面设计过程中,保持设计中心线相对基准轴的水平偏距S为定值。在缓和曲线段,随超高角增大,横断面起点与终点的水平投影位置会逐渐向设计中心线靠拢。
对于曲线段任意一个横断面,设其对应的三次抛物线方程为:y=ax3+bx2+cx+d,其导函数y′=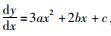
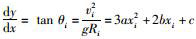
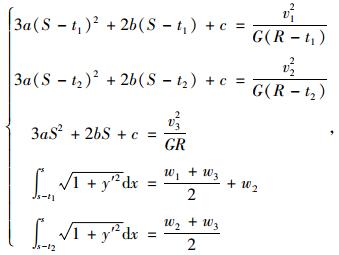
|
(2) |
式中,S为设计中心线与基准线偏距(定值);t1为低速车道中线与高速车道中线的水平投影距离;t2为中速车道中线与高速车道中线的水平投影距离;wi为按弧长定义的各车道宽度;vi为各车道设计控制车速;G为重力加速度, 取9.81 m/s2;R为设计中心线(通常为高速车道中线)位置对应的平曲线曲率半径。
式(2)中,a,b,c,t1,t2为未知数,共5个方程求解,可得唯一的一组解, 由此可确定横断面抛物线方程中系数a,b,c。
对任意平曲线上的断面,如图 3所示,设横断面起点坐标为(x0, 0), 令y=0时,可得式(3):
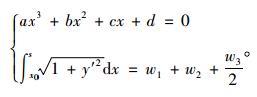
|
(3) |
式(3)中d,x0为未知数,共两个方程求解,可得唯一的一组解。由此可确定横断面抛物线方程中系数d。综上求得曲线段任意横断面三次抛物线方程的所有系数,从而确定平曲线段上每个横断面的设计方程式。
2.2 横断面系数方程组的求解方法由于车道宽度按弧长定义,对于式(2)与式(3)中存在弧长积分方程式,可以运用计算机程序求得其数值解。首先可将a,b,c转换为仅含t1,t2的表达式,代入弧长积分的方程式,然后通过迭代试算来求得t1,t2的值,即假定一组t1,t2的值,通过梯形积分等数值积分方法,求得对应的曲线弧长并与设计车道宽比较,直到两者误差满足精度要求(设计时通常控制为<1 mm),可认为求得t1,t2的数值解,进而求得a,b,c,d的解。
为了满足车道宽误差小于1 mm的工程设计精度要求,计算弧长积分时的积分步长精度控制在0.5 mm,因此t1,t2迭代试算的计算量非常大,步进式求解方法显然不可取。通常可采用二分法、牛顿迭代法等数值计算方法加快数值解收敛速度[7-8]。
同时在求解过程中应充分考虑实际计算模型的物理意义,来缩小t1,t2的试算范围。在平面直缓点位置,即曲线段横断面起算位置,由计算模型可知,此时抛物线断面应非常接近直线段横断面,超高角微小,因此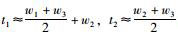
相比于投影宽定义的设计方法,车道宽以弧长定义时需要求非线性方程组的数值解,计算量非常大,与前者呈几何倍数关系。经测试在同等计算机硬件条件下,约为前者计算所需时间的300倍。作为高环核心设计内容,横断面方程系数的计算求解效率非常重要。高效的算法能保证在大数据量的计算条件下,迅速计算得缓和曲线各横断面方程系数的解,以利于进行多方案的比选设计及建模程序调试。
2.3 其他典型横断面设计方法类推上述车道宽度以弧长定义的设计计算模型也适用于其他典型的高环横断面形式。
当设计横断面为4车道时,可以设横断面方程为y=ax3+bx2+cx+d,为保证求解方程组为静定,取其中3个车道的车速进行控制设计,通常为第1,2,4车道,从而形成类似式(2)的静定方程组并进行求解,然后通过求得的抛物线方程反推第3车道的设计车速。
当设计横断面为双车道时,可以设横断面方程为y=ax3+cx+d,对两个车道的车速进行控制设计,形成两个系数未知数方程式与一个弧长积分方程式的方程组进行求解即可。
当设计横断面形式为其他高次抛物线,或复合函数曲线时,该方法也同样可以类推适用。
3 车道宽以弧长定义的设计应用车道宽度以弧长定义的新设计方法,在中汽中心盐城试验场与一汽-大众新建试验场的高环设计中得到了实际应用。
中汽中心试验场的高环设计为4车道横断面,设计采用了y=ax3+cx+d的抛物线形式,通过控制第1、4车道的设计车速对横断面方程进行了计算。由于控制设计车速的车道数仅为两个,计算求解相对更为简单,含a, c的两个未知数方程与一个弧长积分方程式形成求解方程组,求得横断面方程后反推第2车道与第3车道的计算车速。
一汽-大众试验场的高环设计为3车道横断面,设计采用了y=ax3+bx2+cx+d的抛物线形式,对3个车道的车速均进行控制设计,设计模型与计算方法即为上述图 3与式(2)所示。
横断面设计为高环几何设计的核心,文中利用Matlab软件求非线性方程组的数值解[9],得出平曲线段各位置横断面的方程式,参考其他学者的研究成果[10],对高环平纵横进行模块化的综合几何设计与计算,最终得到整个平曲线段上各个横断面计算点的绝对坐标。利用ObjectArx等工具对CAD绘图软件进行了开发[11-13],与模型计算程序交互数据,并建立三维模型,确定了高环三维几何设计的最终形态,同时输出获取设计模型的工程数量等信息。图 4(a)为中汽中心盐城试验场高环局部三维计算机模型。

|
| 图 4 高速环道的设计与实现 Fig. 4 Design and implementation of high-speed track |
| |
建成后的高速环道经过试验车行驶测试,对高环平曲线段的行车舒适性与安全性均有较好评价。通过工程实践验证了车道宽度以弧长定义的新设计方法是行之有效的,能较好地满足高速环道的试车要求。图 4(b)为建成后的实景照片。
4 不同车道宽度定义下的设计比较 4.1 设计方法的理论依据性就车道宽度的设计理念而言,对于高环超高角较大的横断面,车道宽度以弧长定义进行设计在理论上更有依据性。在公路或城市道路设计中,车道宽度的确定实际是综合考虑了车辆轮廓的宽度、超车或并列行驶时需要的侧向余宽、车辆在不同行驶速度下保持横向安全车间距等因素[14-15],即公路设计中车道宽度取3.0~3.75 m是经过详细调查论证并有经验公式计算作为依据的。
在高环横断面设计中,如果设计车道宽度按水平投影定义,那么从直缓点到缓圆点的缓和曲线段内,每个车道的实际路面行驶宽度总是在不断变化增大,而不是一个确定值。在整个平曲线段车道实际行驶的路面宽度是不受设计控制的,而是根据横断面需要的超高角进行推算确定的,虽然也能满足车辆行驶需要,但实际行驶宽度取值缺乏设计依据性。
而当车道宽度以实际行驶路面弧长定义时,整个平曲线段横断面实际行驶路面的宽度是保持不变的,实际路面宽度是由设计所控制的定值。这样的设计宽度取值是具有理论依据的,既满足了车辆的行驶需要,又没有过多的富余。
当高环设计车速较低(通常小于140 km·h-1),设计车道宽度可以参照普通公路的设计宽度取值3.75 m或3.5 m。当高环的设计车速较高时,从理论上车道宽度应再适当加大,以满足车辆高速行驶时横向的安全间距。目前由于缺少这方面的具体研究,只是按照经验当设计车速很高时(通常大于180 km·h-1),设计车道宽度可取4.0~4.5 m。这就意味着设计车道宽度按水平投影定义设计时,实际行驶路面的一个车道弧长可能超过5.0 m,宽度过于富余。
4.2 工程经济合理性与普通公路设计类似,在高环设计时,无论在直线段还是曲线段,设计车速确定后,各个车道的设计宽度总是一个定值。同样满足车辆正常行驶的前提下,采用车道宽度按实际路面弧长定义进行设计,会使整个平曲线段的路基路面工程更为经济合理,主要表现在两个方面:
(1) 平曲线段的道路面积
当车道宽度以水平投影宽定义时,在平曲线段的行驶路面弧长要大于投影长,整个车行道曲面的面积要比车道宽度以弧长定义时大。而实际上多出的面积是由于曲线的弧长大于水平投影而造成的车道宽富余,从工程经济性角度看可以节省。
(2) 整个平曲线段的土方量假设高环在平整的场地上进行填筑,在平曲线段,采用车道宽度以弧长定义进行设计时,其水平投影宽度显然要小于车道宽度以投影定义的设计。因此在平曲线段的每个横断面的几何尺寸就会更小,设计中心线处的高程会更低,从而降低了整个断面的填筑面积,使整个高环平曲线段的土方量减少。且车道数越多,超高角越大的高环,采用车道宽度以弧长定义设计时,平曲线段减少的土方量就越多。
保持设计参数和其他控制条件不变,分别以两种不同的横断面车道宽度定义方法,对某个典型的高环平曲线段横断面进行设计,量化比较其工程数量。部分主要设计参数取值如表 1所示。
| 设计平衡车速/(km·h-1) | 228 | |
| 设计圆曲线半径/m | 470 | |
| 圆曲线段中线超高角/(°) | 41°(圆曲线段) | |
| 设计横断面车道数 | 3车道 | |
| 设计车道宽/m 平衡车速/(km·h-1) | w1=3.5 | v1=80 |
| w2=4.0 | v2=149 | |
| w3=4.5 | v3=228 | |
| 高速车道侧硬路肩宽/m | 1.0 | |
| 一条缓和曲线/m 圆曲线长/m | 469.95 1 033.91 | |
| 断面方程(弧长定义) | y=ax3+bx2+cx+d | |
| 断面方程(投影定义) | y=ax3+bx2+cx | |
在两种不同车道宽度定义方式下,一个平曲线段(缓-圆-缓)的工程数量对比如表 2所示。
| 车道宽定义方式 | 曲线弧长 | 水平投影 |
| 车行道面积/m2 | 25 659 | 29 034 |
| 填方量/m3 | 234 784 | 269 946 |
| 注:表中假设在平整场地上填筑,填方量包括土路肩、堤顶路、边坡等。 | ||
从表 2的计算结果可知,对于上述某个典型的3车道高环设计,车道宽采用弧长定义时,在一个平曲线段内,路面面积节省约13.153%,填方量节省约14.976%。
4.3 施工难度与效率高速环道曲面施工有其特殊性且对质量控制要求较高[16-17]。当采用沥青路面时,需要特殊的曲面摊铺机进行路面结构层的施工[18]。当车道宽度以弧长定义设计时,在整个平曲线段的横断面上,路面弧长宽度总是定值。曲面摊铺机械在平曲线段可维持一个曲线长度移动摊铺,施工速度较快,工程质量更易控制。而当车道宽度以投影宽定义设计时,在缓和曲线段,路面实际弧长宽度在变化。因此施工中需要不断调整摊铺机械的曲线长度,难以连续作业,施工速度相对较低。通常整个路面结构需要逐层(5~6层)摊铺,总周期较长。
5 结论提出了车道宽度以弧长定义的高环横断面设计模型与具体计算方法,其难点在于求解抛物线横断面方程系数的数值解,高效的求解算法非常重要。
新方法在设计计算上更为复杂,但其对车道宽度的定义能更好地符合车辆实际行驶所需的宽度, 在工程运用中更为经济合理。
文中着重介绍了三次抛物线横断面的具体设计模型与计算方法,今后也可进一步类比推广到其他曲线形式的横断面设计中。
| [1] |
张海军, 李进, 林巧飞. 高速环道几何线形设计方法研究[J]. 中外公路, 2007, 27(4): 1-4. ZHANG Hai-jun, LI Jin, LIN Qiao-fei. Study on Geometry Design Method of High-speed Track[J]. Journal of China & Foreign Highway, 2007, 27(4): 1-4. |
| [2] |
李运胜. 高速试验环道几何设计技术研究[J]. 公路交通科技, 1995, 12(2): 1-8. LI Yun-sheng. Geometry Design of High-speed Test Loop[J]. Journal of Highway and Transportation Research and Development, 1995, 12(2): 1-8. |
| [3] |
戴海君. 高速环道线形设计[J]. 中外公路, 2011, 31(6): 59-64. DAI Hai-jun. Alignment Design of High-speed Track[J]. Journal of China & Foreign Highway, 2011, 31(6): 59-64. |
| [4] |
李运胜, 熊选爱. 上海大众试车场高速环道曲面施工[J]. 上海建设科技, 2004(4): 42-43, 47. LI Yun-sheng, XIONG Xuan-ai. The Construction of High Speed Curved Cycling Track of Shanghai Volkswagen Proving Ground[J]. Shanghai Construction Science & Technology, 2004(4): 42-43, 47. |
| [5] |
JTG D20-2006, 公路路线设计规范[S]. JTG D20-2006, Design Specifications for Highway Alignment[S]. |
| [6] |
刘伟民, 蒋永康. 汽车高速环道多平衡车速设计方法[J]. 中国公路, 2014(3): 126-127. LIU Wei-min, JIANG Yong-kang. Design Method on Multi Balance Vehicle Speed on Oval Track[J]. China Highway, 2014(3): 126-127. |
| [7] |
同济大学计算数学教研室. 现代数值数学和计算[M]. 上海: 同济大学出版社, 2004. Teaching and Research Office of Computational Mathematics of Tongji University. Modern Numerical Mathematics and Computation[M]. Shanghai: Tongji University Press, 2004. |
| [8] |
谭振江, 肖春英. 非线性方程数值解法的研究[J]. 吉林师范大学学报:自然科学版, 2014(3): 102-105. TAN Zhen-jiang, XIAO Chun-ying. The Research of the Solution to the Nonlinear Equation[J]. Jilin Normal University Journal:Natural Science Edition, 2014(3): 102-105. |
| [9] |
刘保柱, 苏彦华, 张宏林. matlab 7.0从入门到精通修订版[M]. 北京: 人民邮电出版社, 2010. LIU Bao-zhu, SU Yan-hua, ZHANG Hong-lin. Matlab 7.0 from Entry to Master Rev. ed[M]. Beijing: Posts & Telecom Press, 2010. |
| [10] |
刘伟民. 汽车试验场高速环道几何线形设计研究及程序开发[J]. 城市道桥与防洪, 2012(8): 110-112, 121, 382-383. LIU Wei-min. Geometrical Linear Design Study and Program Develop of Express Oval Track of Automobile Proving Ground[J]. Urban Roads Bridges & Flood Control, 2012(8): 110-112, 121, 382-383. |
| [11] |
刘喜平. 基于AutoLISP的AutoCAD二次开发技术[J]. 机械制造与自动化, 2011(4): 128-129, 146. LIU Xi-ping. Development Technology of Auto CAD Based on AutoLISP[J]. Machine Building & Automation, 2011(4): 128-129, 146. |
| [12] |
杜刚, 刘东学, 张磊. 基于Object ARX的AutoCAD二次开发及应用实例[J]. 机械设计与制造, 2004(3): 30-32. DU Gang, LIU Dong-xue, ZHANG Lei. Secondary Development of AutoCAD Based on Object ARX and its Application[J]. |
| [13] |
张帆, 朱文俊. AutoCAD ObjectARX(VC)开发基础与实例教程[M]. 北京: 中国电力出版社, 2014. ZHANG Fan, ZHU Wen-jun. AutoCAD ObjectARX(VC)Development Basis and Examples of Tutorials[M]. Beijing: China Electric Power Press, 2014. |
| [14] |
郑凤玺, 侯明业, 赵娟娟. 城市道路机动车道宽度研究[J]. 筑路机械与施工机械化, 2013, 30(10): 67-70. ZHENG Feng-xi, HOU Ming-ye, ZHAO Juan-juan. Study on Width of Urban Motor Vehicle Lanes[J]. Road Machinery & Construction Mechanization, 2013, 30(10): 67-70. |
| [15] |
元伟. 城市道路机动车车道宽度研究[D]. 哈尔滨: 哈尔滨工业大学, 2005. YUAN Wei. Study on Carriageway Width of Urban Roads[D]. Harbin:Harbin Institute of Technology, 2005. http://d.wanfangdata.com.cn/Thesis/Y798824 |
| [16] |
孙立国, 张永利. 浅谈高速环道施工管理与质量控制[J]. 科技视界, 2016(19): 224-243. SUN Li-guo, ZHANG Yong-li. Construction Management and Quality Control on High-speed Track[J]. Science & Technology Vision, 2016(19): 224-243. |
| [17] |
徐燕平. 汽车试验道路的设计施工与质量保证[D]. 上海: 上海交通大学, 2007. XU Yan-ping. Automobile Test Road Design, Construction and Quality Guarantee[D]. Shanghai:Shanghai Jiaotong University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10248-2007153836.htm |
| [18] |
卢海燕. 汽车试验场三维曲面环道施工技术及工艺研究[J]. 低碳世界, 2014(11): 281-282. LU Hai-yan. Study on Construction Technology and Process of 3D Curved High-speed Track in Proving Ground[J]. Low Carbon World, 2014(11): 281-282. |
 2017, Vol. 34
2017, Vol. 34
