扩展功能
文章信息
- 杨文臣, 胡澄宇, 田毕江, 房锐
- YANG Wen-chen, HU Cheng-yu, TIAN Bi-jiang, FANG Rui
- 国际平整度指数建模与影响因素综合分析
- Modelling of International Roughness Index and Comprehensive Analysis on Its Influencing Factors
- 公路交通科技, 2017, 34(12): 23-29, 36
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 23-29, 36
- 10.3969/j.issn.1002-0268.2017.12.004
-
文章历史
- 收稿日期: 2017-03-28
道路路面平整度是路面表面相对于理想平面的竖向偏差,直接反映路面的行驶舒适性及安全性[1]。既有路面平整度的评价指标包括3 m直尺下最大间隙、国际平整度指数IRI、平整度标准差σ和功率谱密度PSD等[2]。Sayers等于1982年在巴西等国家进行路面平整度试验[3],提出了国际平整度指数(International roughness index,IRI)。相关研究表明[4],IRI与其他平整度指标有良好的相关性, 是一个比较理想而科学同时又易重现的指标。因此,IRI指标在公路路面施工和验收以及机场道面的评价中获得了广泛应用[5-6]。
多数学者致力于研究IRI与其他平整度评价指标的相关性,如LU、ZHOU等通过理论模型和数值仿真等手段建立IRI和PSD间的关系[7-8];Peter等通过实测路面高程分别建立了刚性路面和柔性路面下IRI和直尺指标SI间的相关性[9];Hall等基于AASHO测试数据研究了路面服务指标PSI与IRI间的关系[10];Lin等研究表明正向和反向传播神经网络可相互估计IRI与路面损害指标[11]。但是,分析IRI评价路面适用性的研究较少,而相同IRI值的路面可能对应不同的纵断面,且IRI与不同行驶速度下人体舒适性的相关性不高[12]。因此,有必要探讨IRI关联的内在影响因素作用机理,科学提取路面不平整评价的重要特征参数。
在实践工作中,由于平整度现场测试速度不一定等于规定的速度(尤其是采用累积颠簸仪测试时),且IRI受现场运动车辆性能、路面性能等因素的综合作用,人们往往会对IRI指标的使用产生误解。针对多数人认为IRI与车速间是单调递增关系的认识,即行驶车速越大,IRI值越大,舒适性越差[13-14],既有研究采用数值计算方法或理论解析方法考察了速度与IRI值的关系。Rohan等基于LTPP路面的实测高程数据,发现车速与IRI值之间的关系复杂而不遵循一定的比例关系[15]。周晓青等从理论上推导IRI的数学解析式,采用简单的简谐激振力函数生成不平整激励,通过设定路面的波长、波幅及行驶距离,选取代表速度采样解析国际平整度指数与速度之间的关系,认为IRI值和行驶速度不是单调递增的关系[14]。这类研究分别从行驶速度或路面性能等角度在一定程度上解析IRI值的分布特性,但受限于模型计算及试验条件,IRI在运行速度和不平整激励共同作用下的特性缺乏定量综合分析;且多数研究为简化计算,采用模拟的简单路面激励,没有解析与实际路面激励的联系与异同。
基于1/4车模型的振动方程,推导IRI的数学计算模型,并将Matlab/ Simulink仿真模块引入IRI求解,在正弦函数、随机路面和实际高程3种路面不平整激励输入下,根据Simulink快速计算的大量仿真结果,绘制影响因素之间的关系图,综合分析IRI值在不同速度、波长和振幅以及空间位置作用下的分布特性,对IRI关联的内在影响因素的作用机理进行探讨。
1 国际平整度指数国际平整度指数IRI是应用力学方法模拟1/4车辆以一定速度沿路面纵断面行驶的反应指标[3],是单位距离内系统的相对竖向位移累计值。
1.1 IRI模型标准的1/4车模型如图 1(a)所示。非簧载质量代表了车辆减震器下部的底盘构件,簧载质量代表了减震器上部的构件。图中Ms为簧载质量; Mu为非簧载质量; Ks为车身悬架刚度系数; Cs为车身悬架阻尼系数; Ku为轮胎刚度系数; q为不平整激励; Zs为簧上质量Ms的绝对位移;Zu为非簧上质量Mu的绝对位移。在不平整激励作用下,1/4车模型动力学响应如图 1(b)所示,根据牛顿第二定律,非簧载质量和簧载质量的振动平衡方程分别如式(1)和式(2)所示:

|
| 图 1 1/4车模型及动力学响应 Fig. 1 Quarter car model and its dynamics response |
| |
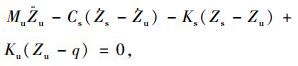
|
(1) |
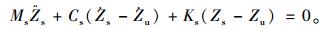
|
(2) |
将式(1)和式(2)两边同时除以Ms,简化后的振动平衡方程如式(3)、(4)所示:
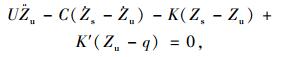
|
(3) |
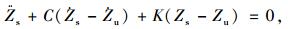
|
(4) |
式中,C=Cs/Ms;K=Ks/Ms;U=Mu/Ms;K′=Ku/Ms。
根据世界银行定义,IRI值为单位距离内簧载质量Ms和非簧载质量Mu的相对位移累计值,由式(5)计算:
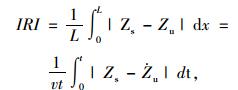
|
(5) |
式中,L为所测路段长度; v为行驶速度; t为行驶时间。
1.2 IRI影响因素在1/4车模型参数固定的条件下,IRI影响因素分析如下:(1)不平整激励:根据式(3)~(4),振动系统中簧载质量和非簧载质量的相对位移累积值与不平整激励直接相关,不同形式的不平整激励将显著影响IRI的分布。(2)行驶速度:行驶速度直接影响振动系统中簧载质量和非簧载质量的竖向位移,且IRI与行驶速度是隐含关系;(3)行驶时间:行驶时间影响不同距离的路段IRI值的分布。对同一路段,由于路面纵断面的不平度序列是运动车辆及路面性能综合作用的结果,为简化分析,研究选取3种不平整路面直接作为激励输入,在不同行驶速度的作用下定量解析IRI变化的方向和强度。
2 模型求解 2.1 求解方法式(3)~(4)的振动微分方程描述了标准车模型在不平整激励下的动力学响应,可采用解析法或数值法进行求解。解析法通过建立复杂的数学函数计算位移、速度和加速度等解析解,并采用式(5)计算IRI值。由于道路路面高程函数的不连续性,难以采用统一的数学函数对其进行表征,在实践中通常采用数值迭代计算的方法求解IRI值,如姚祖康提出的调整坡(RS)解法[16]、交通运输部采用Basic语言编写相应的计算机程序[17]、世界银行提出的传递矩阵计算程序[3]。但数值法对IRI值的计算过程多,工作量大,灵活性较差,大量求解的效率低,难以支撑不同行驶工况条件下IRI值与多维影响因素间数值关系的综合分析。
Matlab/Simulink提供一个动态系统建模、仿真和综合分析的集成环境,具有仿真精细、效率高且灵活的优点。为了解析IRI在不同行驶条件下的演化特性,本研究采用Simulink模块快速地数值仿真求解IRI模型。1/4标准车的动力学系统的Simulink仿真模型如图 2所示,IRI模型的Simulink建模的流程如下:(1)确定不平整路面激励q,作为整个系统的输入;(2)建立以簧载质量和非簧载质量的加速度为核心的子系统,并根据式(3)和(4)连接各子系统;(3)在系统中配置标准1/4车模型的各个参数;(4)根据运行速度和不平整激励长度确定仿真时间;(5)仿真并根据各子系统的输出,采用式(5)计算IRI值;(6)定量综合分析仿真结果。

|
| 图 2 IRI求解的Simulink模型 Fig. 2 Simulink model for solving IRI |
| |
2.2 不平整激励生成
当前不平整激励生成方法主要有:正弦函数、随机路面和实测路面,然而,多数研究只单一地分析某种激励对IRI的影响。为全面分析IRI与路面性能、运行速度等关联内在影响因素的关系,本文综合分析了3种不平整度激励形式下IRI分布的异同。
(1) 正弦函数不平整激励[18]
随着公路路面服役时间的增加,其纵断面上会产生微波起伏,这种波动可近似地采用正弦函数来模拟表示,如式(6)所示。
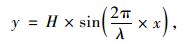
|
(6) |
式中,H为振幅;λ为波长;x为路面纵断面的前进方向;y为纵断面的相对高程。
(2) 随机路面不平整激励
若将路面视作连续曲面,可认为路面纵断面的平整度序列是一种随机现象,服从高斯概率分布的零均值各态历经随机场。这种平稳随机变化过程具有平稳遍历特性,可采用功率谱密度函数来描述路面特征,可看作是相对平整路面产生的平稳随机噪声。根据《车辆振动输入路面平度表示方法》(GB7031—86),在空间频率n1<n<n2的条件下,路面功率谱Gq(n)的拟合表达式如式(7)所示[19]:
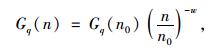
|
(7) |
式中,Gq(n0)为路面不平度系数,对应A~F级路面;n0为参考空间频率,取0.1 m-1;w为频率指数,取2。
(3) 实测高程路面不平整激励
在道路交通荷载及周围环境的综合作用下,纵断面不平整起伏的特性往往比正弦函数不平整激励和随机路面不平整激励复杂得多,目前通常采用激光断面仪实测的路面高程序列表征这种客观的不平整激励。
3 模型分析 3.1 试验描述为综合分析IRI与路面性能、运行速度等关联内在影响因素的作用机理,分别采用2.2节中3种路面的不平整激励作为输入,设计3种试验场景。
(1) 不平整激励路面
利用上海某公路路段长度为3 000 m的实测路面高程作为不平整激励,每隔0.25 m采集一个点的相对高程,实测道路不平整激励如图 3所示。为统一分析的基准,随机路面不平整激励的长度取为3 000 m,相邻两采样点的水平距离取为0.25 m。聂彦鑫等研究发现路面统计的空间频率分布在[0.11, 2.83],利用谐波叠加法则可生成随机铺面的纵断面[20],A级路面形式如图 4所示。正弦函数不平整激励通过设定不同代表振幅和波长的参数值进行模拟。

|
| 图 3 实测道路不平整激励 Fig. 3 Field measured pavement roughness excitation |
| |

|
| 图 4 A级不平整随机激励 Fig. 4 Class A pavement roughness excitation |
| |
(2) 试验设计
试验1:正弦函数不平整激励的综合分析。采用正弦函数不平整激励分析不同振幅、波长及运行速度作用下的IRI值的分布特性。试验方案中运行距离采用单倍波长,参数设计如下:①为分析振幅与IRI值关系,选择代表性波长和行驶速度,振幅取值0~0.1 m,仿真步长为0.001 m;②为综合分析运行速度和波长对IRI值的综合作用,控制振幅为0.003 m,行驶速度取值0~120 km/h,波长取值0.5~30 m,速度、波长的仿真步长分别为1 km/h,0.1 m。
试验2:随机路面不平整激励的综合分析。采用随机路面不平整激励分析不同速度作用下IRI值的分布特性,并解析路段上不同空间位置的IRI值分布的差异性。试验方案的参数设计如下:①为分析整条道路平均IRI值的总体分布,行驶速度取值0~120 km/h,仿真步长为1 km/h;②为分析道路上不同空间位置IRI值的空间分布,将随机道面等距离划分为10段,每个分段内行驶速度取0~120 km/h,仿真步长为10 km/h。
试验3:实测路面不平整激励的综合分析。采用路面实测高程的不平整激励分析不同速度作用下IRI的分布特性。试验方案的参数设计与试验2相同,分别考查整条道路和路段不同空间位置的IRI分布特性。根据图 3的实测高程数据,各分段激励的特征如表 1所示。
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 趋势 | 增大 | 增大 | 平稳 | 平稳 | 减小 | 增大 | 减小 | 增大 | 减小 | 减小 |
| 波动 | 较小 | 较大 | 大 | 较小 | 较小 | 较小 | 较小 | 大 | 大 | 较大 |
| 噪声 | 不明显 | 不明显 | 明显 | 明显 | 明显 | 明显 | 明显 | 不明显 | 不明显 | 不明显 |
3.2 结果分析 3.2.1 正弦函数不平整激励
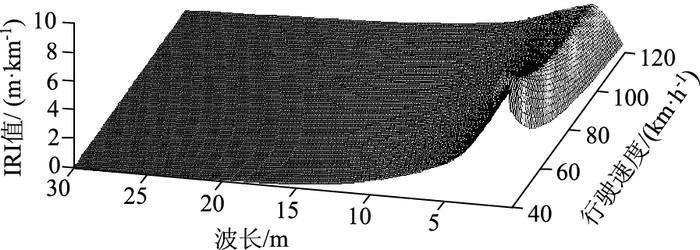
PIARC将引起路面不平整度的路面波长范围分为短波、中波和长波,其中短波0.5~5.0 m、中波5.0~15 m、长波15~50 m[21]。在正弦函数不平整激励作用下,选取短波(2 m)、中波(8 m)、长波(20 m)为代表性波长,不同振幅水平IRI值的分布如图 5所示,路面IRI值与振幅均成正比例关系,且振幅与IRI值间的比例系数随波长和行驶速度的变化而变化。控制振幅为0.003 m时,不同行驶速度及波长下IRI值的分布如图 6所示。IRI值与速度不是呈简单的单调递增或递减的关系,IRI值取决于波长和行驶速度的综合作用。存在一个短波的敏感波段(1~5 m)使得IRI值达到最大,在中波范围内,IRI值逐渐下降且变化相对缓和,IRI值对长波不平整激励不敏感。同时,存在一个中低速的速度区间使得IRI值处于最大水平,此后IRI值逐渐下降,且随着速度的增加下降趋于平缓,但IRI值仍维持在较高水平。

|
| 图 5 不同振幅下IRI值分布 Fig. 5 IRI distributions with different vibration amplitudes |
| |
|
| 图 6 不同行驶速度及波长下IRI值分布 Fig. 6 IRI distributions with different wavelengths and speeds |
| |
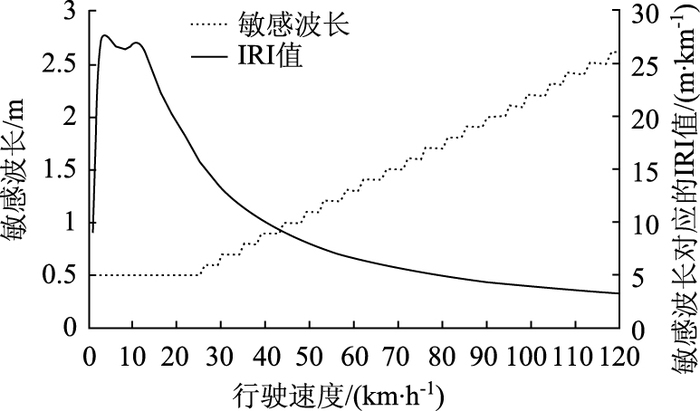
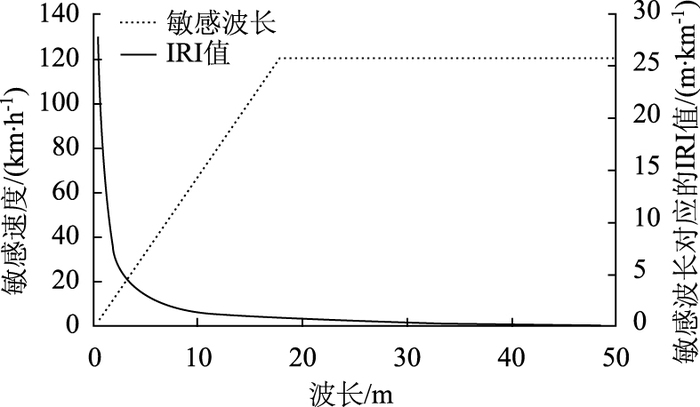
定义最大IRI值对应的波长和速度分别为敏感波长和敏感速度。在正弦函数不平整激励作用下,IRI值的敏感波长和敏感速度的分布分别如图 7和图 8所示。整体而言,IRI值随行驶速度的增大呈先增加后减小的趋势,且当速度大于11 km/h时,IRI值呈指数急剧下降;IRI值随波长的增加呈急剧下降,当波长大于20 m时,IRI值接近于0。
|
| 图 7 不同行驶速度下IRI值的敏感波长分布 Fig. 7 Sensitive wavelength distribution of IRI with different speeds |
| |
|
| 图 8 不同波长下IRI值的敏感速度分布 Fig. 8 Sensitive speed distribution of IRI with different wavelengths |
| |
对于敏感波长,当速度小于25 km/h时,IRI值对应的敏感波长为0.5 m,而对40~120 km/h的速度,敏感波长分布在0.5~2.7 m之间,且敏感波长与速度成正比关系。对于敏感速度,当波长大于18 m时,IRI在120 km/h的速度下响应达到最大;对0~18 m的中短波,敏感速度则随着波长的增加而增加。
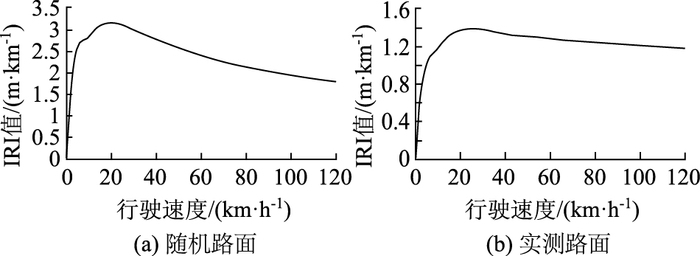
3.2.2 随机及实测不平整激励不同行驶速度下随机及实测路面IRI值的总体分布如图 9所示。随机路面和实测路面的IRI值与行驶速度的关系相似,IRI值与行驶速度均呈现先增大后减小的趋势,而不是简单的单调关系;同时,由于随机与实测两种路面的不平整激励的特征(趋势、波动、噪声)存在显著差异,二者的曲线特征存在明显不同:随机道面的IRI值上升速度快,达到最大IRI值后(20 km/h时),IRI值呈指数快速下降(减小约50%),而实测道面的IRI值在30 km/h左右达到最大,此后呈线性缓慢下降(减小约15%),IRI值则一直保持在较高的水平。
|
| 图 9 不同行驶速度下随机及实测路面IRI值的总体分布 Fig. 9 IRI distributions of random and measured pavements with different speeds |
| |
根据图 9(b),考虑到实际公路上车辆的行驶速度呈S型分布,与选择低速对应的IRI最大值作为路面不平整的评价标准值相比,选取绝大多数车辆的平均速度对应的IRI值将更具代表性:在公路上车辆行驶速度分布为40~120 km/h,选取平均值80 km/h速度对应IRI值作为路面评价准则具有一定的合理性。
3.2.3 不同空间位置不同行驶速度下各路段IRI值的空间分布如图 10所示。对随机路面,不同行驶速度下各路段的IRI值的分布一致,与图 9(a)整线IRI值的总体分布相似,均呈先增大后减小趋势,IRI值随速度的梯度变化明显,这是因为随机路面采用零均值各态历经随机场生成不平整激励,平稳的随机噪声使得每个分段内不平整激励的规律相同。对实测路面,多数路段整体上与图 9(b)整线IRI值的总体分布相似,随着速度的增加呈现先增大后减小趋势,但是由于每个路段的不平整激励的特征不同,不同行驶速度下各路段IRI值的分布存在较明显的差异。

|
| 图 10 不同行驶速度下各路段IRI值的分布 Fig. 10 IRI distributions of each road section with different speeds |
| |
具体而言,根据表 1各实测路段的路面特征,平整的路面“趋势”可看作是波长无限大的正弦函数不平整激励的一部分,由3.2.1节分析可知,IRI值对长波的不平整激励不敏感,即平整的路面“趋势”对IRI不产生贡献;路面的“波动”大小可看作是正弦函数不平整激励的振幅大小,因而“波动”越大,对IRI值影响越大;路面“噪声”对IRI值的影响则可以看作是平稳随机路面的影响。上述实测路段的路面特性在图 10(b)中得到反映:编号3,8,9,10的路段IRI值较大,编号1和4的路段IRI值较小,其他路段IRI值相当。这是因为路段3,8,9存在明显的大振幅波动,使得相应路段的IRI值最大;路段1的IRI值小是因为不平整激励的波动较小且无明显噪声点;路段4存在明显噪声,但其趋势平稳且波动的变化相对缓慢,与随机路面形式较为接近,其IRI值随速度的梯度变化最为显著。
可见,对实测路面,路面的“波动”对IRI值的影响贡献最大,而路面的“噪声”对IRI值的贡献影响次之,平整的路面“趋势”基本不对IRI值产生贡献。因而,对于IRI值的变化而言,实测的不平整激励在一定程度上可看作是不同波长的正弦函数不平整激励和随机不平整激励的多元复杂组合。由于这两类的不平整激励的敏感速度各不相同,对具有不同路面特征的实测路段,见图 10(b),其IRI值敏感速度分布表现出差异性。
4 结论(1) 不同形式路面激励所发现的IRI值分布特性比较一致,IRI值与速度关系整体上均呈现出先增加后减小的趋势,而非传统认知的简单单调关系。
(2) 不同速度下IRI值与振幅成正比,IRI值的敏感波段均位于0.5~2.7 m的短波范围,实测路面的IRI值与速度的关系与路面的趋势、波动和噪声等特性有关。
(3) 正弦函数不平整激励可用于解析路面起伏的波长和振幅对IRI值的作用机理,可描述实测路面的趋势和波动部分;随机路面不平整激励可用于模拟路面随机噪声下IRI值于不同速度分布下的总体分布规律,可描述实测路面的噪声部分。
(4) 不同形式的路面不平整激励适用于不同IRI值特性的综合分析,实测不平整激励可看作是不同波长的正弦函数和随机函数不平整激励的复杂组合,因此现实复杂路面条件下各路段的IRI值随速度的分布各不相同。
| [1] |
ASTM E867-2006, Standard Terminology Relating to Vehicle-Pavement Systems[S].
|
| [2] |
周晓青, 孙立军, 颜利. 路面平整度评价发展及趋势[J]. 公路交通科技, 2005, 22(10): 18-22. ZHOU Xiao-qing, SUN Li-jun, YAN Li. Research Progress and Trend of Pavement Roughness Inidces[J]. Journal of Highway and Transportation Research and Development, 2005, 22(10): 18-22. |
| [3] |
SAYERS M W, GILLESPIE T D, QUEIROZ C A V. The International Road Roughness Experiment:Establishing Correlation and Calibration Standard for Measurements[R].[S.l.]:World Bank Technical Paper, 1986.
|
| [4] |
张峰. 公路工程中的平整度评价指标[J]. 公路与汽运, 2004(2): 42-44. ZHANG Feng. Evenness Evaluation Indexes of Highway Engineering[J]. Highways and Automotive Applications, 2004(2): 42-44. |
| [5] |
JTG F40-2004, 公路沥青路面施工技术规范[S]. JTG F40-2004, Technical Specifications for Construction of Highway Asphalt Pavements[S]. |
| [6] |
MH/T 5024-2009, 民用机场道面评价技术管理规范[S]. MH/T 5024-2009, Technical Specifications of Aerodrome Pavement Evaluation and Management[S]. |
| [7] |
SUN L. Simulation of Pavement Roughness and IRI Based on Power Spectral Density[J]. Mathematics and Computers in Simulation, 2003, 61(2): 77-88. |
| [8] |
周晓青, 颜利, 孙立军. 国际平整度指数与路面功率谱密度相关关系研究及验证[J]. 土木工程学报, 2007, 54(1): 99-104. ZHOU Xiao-qing, YAN Li, SUN Li-jun. Study and Validation of the Relationship between International Roughness Index and Power Spectral Density[J]. China Civil Engineering Journal, 2007, 54(1): 99-104. |
| [9] |
MUCKA P. Relationship between International Roughness Index and Straightedge Index[J]. Journal of Transportation Engineering, 2012, 138(9): 1099-1112. |
| [10] |
HALL K T, CORREA C E. Estimation of Present Serviceability Index from International Roughness Index[J]. Transportation Research Record, 1999, 1655: 93-99. |
| [11] |
LIN J D, YAU J T, HSIAO L H. Correlation Analysis between International Roughness Index (IRI)and Pavement Distress by Neural Network[C]//Transportation Research Board 82th Annual Meeting. Washington, D.C.:TRB, 2003:1-21.
|
| [12] |
KROPAC O, MUCKA P. Be Careful When Using the International Roughness Index as an Indicator of Road Unevenness[J]. Journal of Sound and Vibration, 2005, 287(4/5): 989-1003. |
| [13] |
王建锋, 宋宏勋, 马荣贵. 路面平整度评价指标IRI的影响因素[J]. 重庆交通大学学报:自然科学版, 2012, 31(6): 1145-1148. WANG Jian-feng, SONG Hong-xun, MA Rong-gui. Influencing Factors of International Roughness Index[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2012, 31(6): 1145-1148. |
| [14] |
周晓青, 孙立军. 国际平整度指数与行驶车速的关系[J]. 同济大学学报:自然科学版, 2005, 33(10): 47-51. ZHOU Xiao-qing, SUN Li-jun. Relationship between International Roughness Index and Velocity of Quarter Car[J]. |
| [15] |
PERERA R, KOHN S. Effects of Variation in Quarter-Car Simulation Speed on International Roughness Index Algorithm[J]. Transportation Research Record, 2004, 1889: 144-151. |
| [16] |
姚祖康. 路面管理系统[M]. 北京: 人民交通出版社, 1993. YAO Zu-kang. Pavement Management System[M]. Beijing: China Communications Press, 1993. |
| [17] |
JT/T 676-2009, 车载式路面激光平整度仪[S]. JT/T 676-2009, Vehicle Bearing Road Laser Profilometer[S]. |
| [18] |
周晓青. 机场道面平整度评价指标研究[D]. 上海: 同济大学, 2006. ZHOU Xiao-qing. Study on Airport Pavement Roughness Evaluation[D]. Shanghai:Tongji University, 2006. http://d.wanfangdata.com.cn/Thesis/W1657669 |
| [19] |
GB7031-86, 车辆振动输入路面平度表示方法[S]. GB7031-86, Vehicle Vibration-Describing Method for Road Surface Irregularity[S]. |
| [20] |
聂彦鑫, 李孟良, 过学迅, 等. 基于谐波叠加法的路面不平度重构[J]. 汽车科技, 2009(4): 55-58. NIE Yan-xin, LI Meng-liang, GUO Xue-xun, et al. Road Roughness Simulation Based on Partial Wave Adding Model[J]. |
| [21] |
姚祖康. 公路设计手册-路面[M]. 北京: 人民交通出版社, 1999. YAO Zu-kang. Manual of Highway Design:Pavement[M]. Beijing: China Communications Press, 1999. |
 2017, Vol. 34
2017, Vol. 34
