扩展功能
文章信息
- 许海亮, 何兆才, 何炼
- XU Hai-liang, HE Zhao-cai, HE Lian
- 车路耦合条件下沥青混凝土路面变形特性时域分析
- Analysis on Asphalt Concrete Pavement Deformation Characteristics Time-domain Considering Vehicle-pavement Coupling Effect
- 公路交通科技, 2017, 34(12): 16-22
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 16-22
- 10.3969/j.issn.1002-0268.2017.12.003
-
文章历史
- 收稿日期: 2017-03-14
车辆在路面不平整度的激励下产生振动,这种振动反过来又作用于道路结构,引起道路结构的变形,进而又加剧了车辆的振动,这是一个典型的车路耦合作用问题[1-3]。目前,对于道路结构在车辆荷载作用下变形问题的研究主要采用以下几种方式:(1)利用车辆模型,研究路面随机不平整度激励下车辆的振动,并计算出车辆对路面结构的动力荷载,再以该荷载来研究路面结构的响应[4-5];(2)直接假定某种波动荷载为模拟的车辆荷载进行道路结构的动力响应研究[6-7];(3)建立车路耦合线弹性模型,利用随机振动相关理论采用频域分析方法对问题进行研究[8-9]。方法(1)、(2)都将车辆和道路系统分离进行研究,没有完全反映出车路耦合振动的实际状况;方法(3)一般利用线弹性模型,在频域内对问题进行研究,但是方法(3)还存在不足:利用线性模型得到的频域分析结果都是中心化的,对于振动响应的描述并不全面;虽然通过对频率响应的逆变化可以得到振动的时域表达,但是得不出道路某一断面的振动特性。针对上述方法研究中的不足,为了更为全面地研究车路耦合随机振动问题,本文利用Ansys有限元数值模拟方法,通过建立车路耦合系统的非线性数值模型,在时域范畴内,对沥青混凝土路面结构变形问题进行研究[10-13]。
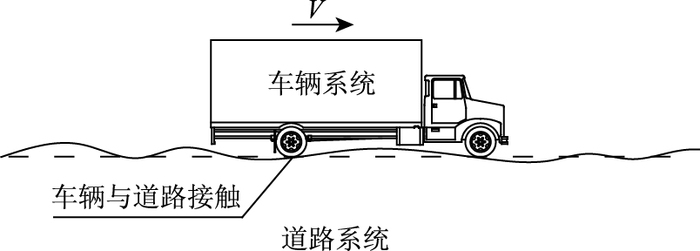
1 车路耦合系统非线性数值模型的建立车路耦合系统非线性模型的建立包括3个大的部分:车辆系统、道路系统以及车辆与道路的接触,如图 1所示。图示系统中包含着大量非线性因素,为了避免考虑太多非线性因素而对问题的数值求解收敛带来困难,本文模型中只考虑了车辆与道路的接触非线性问题,建立了系统的二维数值模型。
|
| 图 1 车路耦合系统非线性模型描述 Fig. 1 Illustration of vehicle-pavement coupled system nonlinear model |
| |
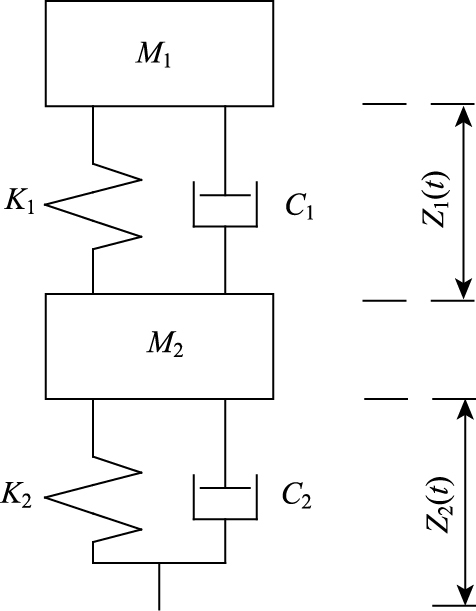
在数值模型中车辆仍采用1/4车辆模型,据相关的国内外研究资料表明[5, 14],该车辆模型在相关的研究中应用较为广泛,能满足计算精度需求。车辆模型如图 2所示。
|
| 图 2 四分之一车辆模型 Fig. 2 Quarter vehicle model 注:M1—悬挂系统(车架、载重)的质量;M2—非悬挂系统(轮胎、轮轴)的质量;K1—悬挂系统刚度;K2—非悬挂系统刚度;C1—悬挂系统阻尼;C2—非悬挂系统阻尼;Z1—悬挂系统与非悬挂系统的相对位移;Z2—非悬挂系统与路面的相对位移。 |
| |
对于图 2所示的车辆力学模型,分别采用了质量单元MASS21和弹簧阻尼单元COMBIN14进行模拟。
沥青混凝土路面结构通常是由多层材料组成,根据道路结构设计组成,路面分上面层、中面层、下面层3个层次建模,路基分为基层、垫层和土路基3个层次建模。层间作用考虑为连续无滑动。道路结构分析单元取用2维实体结构单元PLANE42和PLANE2进行。由于需要在时域内进行计算,路面不平整度需要被表达成空间形式。本文通过对路面不平整度频谱进行Fourier逆变换得到路面不平整度的时域模拟样本。利用ANSYS软件提供的二次开发平台,采用APDL参数化设计语言编写了相应程序,完成对路面不平整度的空间形式的建模。
建立车路耦合关系模型中采用了动点激振模型。将车辆作用力分布在长度为0.2 m的线荷载上。选用单元CONTA48描述车辆与路面的接触和跳起。模型中没有考虑轮胎与路面间摩擦力的影响。
选定道路模型尺寸分别为:长度方向40 m,深度方向3 m。长度方向40 m可以基本保证按车辆常用速度有1 s以上的运行时间,现有的研究资料表明,深度方向取3 m也可以保证大于车辆动荷载在道路内的作用范围。鉴于车辆荷载对道路的影响范围有限,道路模型的边界条件都定为固定约束。
建立车路耦合非线性二维模型如图 3所示。对模型进行单元划分后,共生成9 458个单元,12 967个节点。模型计算过程中,车辆模型在道路表面以某一设定速度匀速运动。

|
| 图 3 车路耦合非线性模型 Fig. 3 Vehicle-pavement coupled system nonlinear model |
| |
车辆道路耦合系统非线性模型,能够在时域内反映车辆道路系统的耦合振动,得到系统响应的时程变化情况,是一个相对更能真实反映车辆道路系统实际振动的模型。通过与已有现场实测振动波形的对比表明,本文非线性模型与实测资料总体趋势能较好地符合,计算结果数值可信。
2 研究工况及参数取值本章利用非线性模型,分别研究了不同路面不平整度、不同车辆行驶速度、不同车辆载重和不同路基强度等影响因素下的道路结构振动响应情况。考虑道路结构本身的复杂性,每一结构层对振动的响应均会表现不同,为了突出和便于比较影响因素下的变化趋势,本文取路表位移响应作为研究对象。路表位移(弯沉值)是道路设计和道路现状评价的重要指标,因此选取路表位移响应作为研究对象是合适的。由于路面不平整度的随机性,使计算得到的道路结构响应值本身也具有随机性,因此在上述研究内容中均采用计算范围内最大响应节点的数值进行对比分析。
在下文的各项计算中,如无特殊说明均按以下参数取值[14-15]:M1取1 350 kg,M2取150 kg,K1取1.5×105 N/m,K2取4.5×105 N/m,C1取4.5×105(N·s)/m,C2取1.5×103(N·s)/m,v=20 m/s(72 km/h),重力加速度取9.81 m/s2。
| 结构层名称 | 厚度/cm | 弹性模量/MPa | 泊松比 | 密度/(kN·m-3) | |
| 面层 | 上面层 | 4 | 1 200 | 0.25 | 2.0 |
| 中面层 | 5 | 1 150 | 0.25 | 2.0 | |
| 下面层 | 7 | 1 100 | 0.25 | 2.0 | |
| 基层 | 40 | 900 | 0.3 | 1.9 | |
| 垫层 | 20 | 600 | 0.35 | 1.9 | |
| 路基 | 224 | 25 | 0.42 | 1.9 | |
3 路面不平整度对路面结构振动的影响
我国运营道路的路面不平整度绝大部分分布在A, B, C三级[16-17],特别是近年来大量修建的高等级公路,路面不平整度主要分布在A级,因此在路面不平整度对道路结构振动的影响研究中,路面不平整度时域模型只采用A, B, C三级,分级标准如表 2所示。
| 路面等级 | Gd(n0)/(×10-6 m3) (n0=0.1 m-1) 几何平均值 | σd/(×10-3 m2) (0.011 m-1<n<2.83 m-1) 几何平均值 |
| A | 16 | 3.81 |
| B | 64 | 7.61 |
| C | 256 | 15.23 |
| D | 1 024 | 30.45 |
| E | 4 096 | 60.90 |
| F | 16 384 | 121.80 |
| G | 65 536 | 243.61 |
| H | 262 144 | 487.22 |
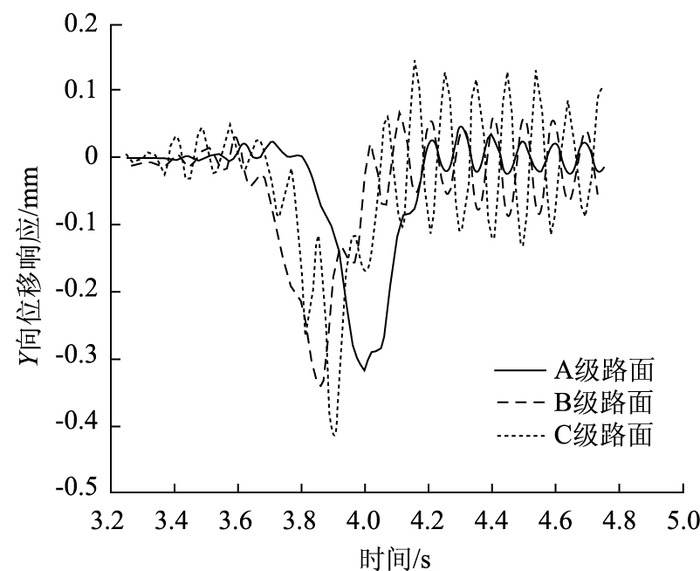
图 4为车辆行驶速度为v=20 m/s(72 km/h),路面不平整度分别为A, B,C三级条件下路面竖向位移的时程响应对比图。计算显示,A级路面情况下,最大位移量为0.318 3 mm;B级路面情况下,最大位移量为0.341 5mm;C级路面情况下,最大位移量为0.417 1 mm。通过对比图形和数据可以得到以下结论:
|
| 图 4 不同路面不平整度条件下路面位移时程响应对比图 Fig. 4 Comparative pavement displacement-time response curves with different pavement ruoghnesses |
| |
(1) 无论在何种路面条件下行驶,道路位移响应都可以明显地分为3个阶段,暂称为:车辆临近、车辆进行和车辆离去。车辆临近和车辆离去阶段的振动频率明显高与车辆进行阶段,可以看出路面结构对于高频成分的作用力更为敏感;车辆进行阶段的位移量最大,可以看出路面结构变形量值主要受车辆自身重量控制;车辆离去阶段的频率和振幅均大于车辆临近阶段,这主要是由于车辆离去阶段路面结构本身恢复变形产生的振动和车辆产生的振动叠加共振的结果。
(2) 由图中可以看出,路面平整度越差产生的振动频率和位移也越大,C级路面下的最大位移量是A级路面的1.31倍;而在车辆离去阶段C级路面下的位移量是A级路面下的2~3倍。
4 车行驶速度对路面结构振动的影响车辆行驶速度对道路结构的响应有重要的影响,主要体现在两方面:一方面车辆行驶速度的改变使道路结构受车辆作用力的时间随之发生改变;另一方面车辆行驶速度不同,使同一路面不平整度产生随机激励的频率也不同。由此可见,车速对道路结构振动响应的影响是重要的也是十分复杂的。
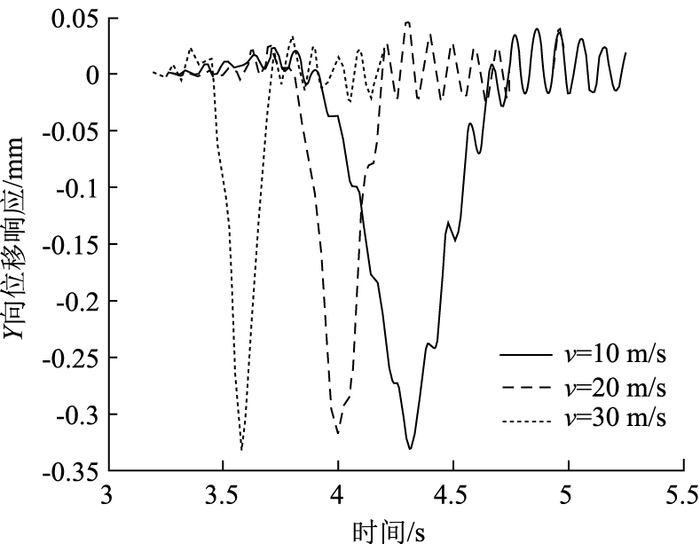
图 5为A级路面不平整度条件下车辆行驶速度的对比图。车辆行驶速度分别采用v=10 m/s(36 km/h)、v=20 m/s(72 km/h)和v=30 m/s(108 km/h)3个车辆常见车速。
|
| 图 5 不同速度条件下路面位移时程响应对比图(A级路面) Fig. 5 Comparative pavement displacement-time response curves with different speeds (Class A pavement) |
| |
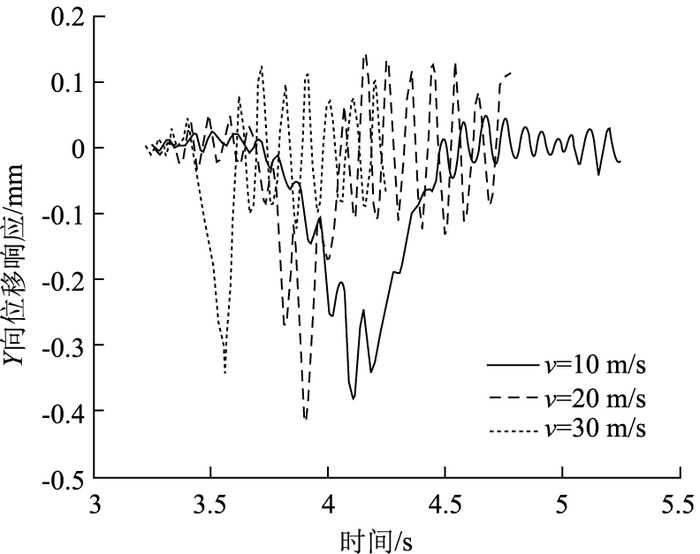
图 6为C级路面不平整度条件下车辆行驶速度的对比图。
|
| 图 6 不同速度条件下路面位移时程响应对比图(C级路面) Fig. 6 Comparative pavement displacement-time response curves with different speeds (Class C pavement) |
| |
同样对B级路面也进行了相关计算,表 3列出了各个工况下路面位移响应的最大值。
| 路面等级 | 位移/m | ||
| 10 m/s | 20 m/s | 30 m/s | |
| A | 0.332 66 | 0.318 30 | 0.333 50 |
| B | 0.351 15 | 0.341 50 | 0.329 94 |
| C | 0.380 29 | 0.417 07 | 0.343 44 |
(1) 车辆行驶速度越低,其车辆进行阶段的时长越长,该过程中出现的位移振动峰值也越多,以图 6所示C级路面不同速度下的路面位移响应为例,在以10 m/s速度行驶时,车辆进行阶段的时长约0.5 s左右,共出现4处明显的位移峰值;在以20 m/s速度行驶时,车辆进行阶段的时长约0.3 s左右,共出现3处明显的位移峰值;在以30 m/s速度行驶时,车辆进行阶段的时长约0.15 s左右,只有1处明显的位移峰值。
(2) 通过图形分析,在车辆进行阶段出现的一些小的位移振动峰值主要受路面不平整而引起的随机振动影响,而且这些小的振动峰值随着路面不平整度的变差而增大。
(3) 已有的研究成果显示[18],在相同路面条件下随着车辆行驶速度的增大,路面最大位移量变小。观察表 2中的数据,可以发现相同的变化趋势(除去两个奇异点数据),但是最大位移量随速度的变化幅度很小,趋势不是很明显。
5 超载车辆对路面结构振动的影响超载是目前困扰我国公路运行的一个普遍性问题。据有关的车辆及装载情况调查,发现超载车辆的比例超过了50%,而且超载率很多都在80%~120%,甚至达到了300%。
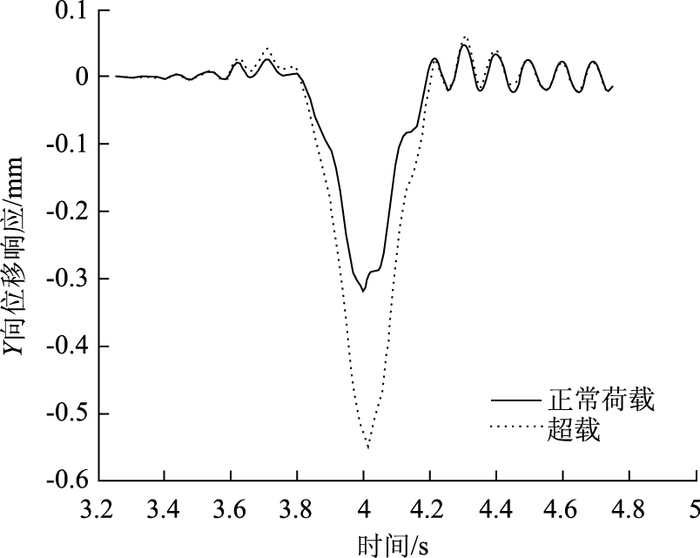
为研究超载车辆对道路结构的振动响应影响,将模型参数中M1取值由原来的1 350 kg提升为2 700 kg,图 7为车速v=20 m/s(72 km/h)A级路面条件下超载前后路面位移响应对比图形。
|
| 图 7 A级路面条件下位移时程响应对比图(v=20 m/s) Fig. 7 Comparative pavement displacement-time response curves (Class A pavement, v=20 m/s) |
| |
对其他工况也进行了相关计算,表 4列出了各个工况下,超载前后路面最大位移值。
| 路面等级 | 车速/(m·s-1) | 正常荷载 | 超载 | 增大幅度/% |
| A | 20 | 0.318 3 | 0.551 7 | 73 |
| B | 20 | 0.341 5 | 0.591 9 | 73 |
| C | 20 | 0.417 1 | 0.627 4 | 50 |
| B | 30 | 0.329 9 | 0.689 7 | 109 |
(1) 车辆超载后,路面最大位移量增大明显,统计以上计算的4种工况,超载比例达到100%情况下,路面变形增大幅度在50%~109%之间,超出了路面允许弯沉值,是加速路面破坏减少使用寿命的重要因素。
(2) 超载对于车辆临近阶段和车辆离去阶段的路面振动影响较小,对比图形可以看出,超载对于这两个阶段的振动频率没有任何影响,仅振动幅值微增。由此可以看出,路面高频部分的振动受车辆荷载的变化影响不大。
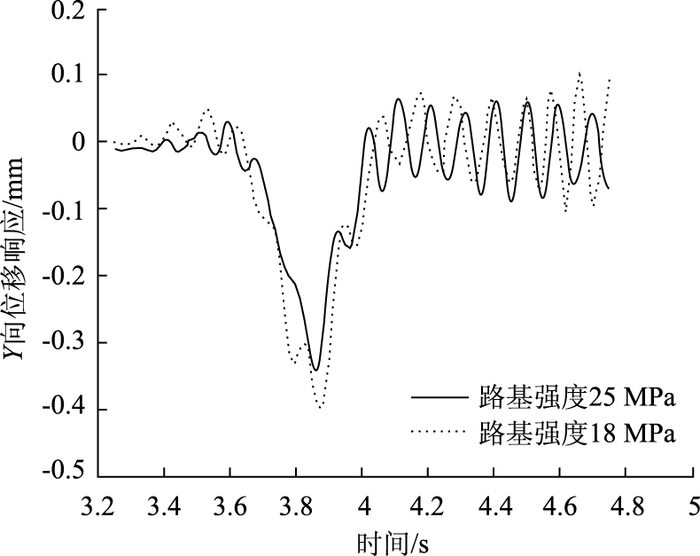
6 路基状况对路面结构振动的影响近年来随着我国公路事业的蓬勃发展,出现了不少修建在软土地区的高等级公路。这些地区经简单地基处理后,路基回弹模量一般能达到17~20 MPa左右。为研究路基强度对道路结构的振动响应影响,将模型参数中路基的弹性模量取值由原来的25 MPa降为18 MPa。图 8为车速v=20 m/s(72 km/h)B级路面条件下路基强度变化前后路面位移响应对比图形。
|
| 图 8 B级路面条件下位移时程响应对比图(v=20 m/s) Fig. 8 Comparative pavement displacement-time response curves (Class B pavement, v=20 m/s) |
| |
表 5列出了各个工况下,路基强度变化前后路面最大位移值。
| 路面 等级 | 车速/ (m·s-1) | 最大位移响应值/mm | 增大幅度/ % | |
| 路基强度 25 MPa | 路基强度 18 MPa | |||
| B | 20 | 0.341 5 | 0.400 9 | 17.4 |
| B | 30 | 0.329 9 | 0.379 2 | 14.9 |
(1) 路基强度降低后,路面最大位移量明显增大,统计以上计算的2种工况,路基强度降低28%后,路面变形增大幅度在15%左右。这说明路基强度对于路面的最大位移量影响很大,所以软土地区道路工程中对路基处理显得格外重要。
(2) 路基强度降低后对车辆临近阶段和车辆离去阶段的路面振动影响也很大,主要体现在这两个阶段的振动频率降低,振动幅值增加。由此可以看出路面高频部分的振动受道路结构本身性质的影响较大。
7 结论(1) 无论在何种路面条件下行驶,道路位移响应都可以明显地分为3个阶段,暂称为:车辆临近、车辆进行和车辆离去。
(2) 路面平整度越差,路面结构位移也越大,C级路面下的最大位移量是A级路面的1.31倍;而在车辆离去阶段C级路面下的位移量是A级路面下的2~3倍。
(3) 路面响应的最大位移峰值主要受车辆自重影响,而在车辆进行阶段出现的一些小的位移振动峰值主要受路面不平整而引起的随机振动影响,而且这些小的振动峰值随着路面不平整度的变差而增大。
(4) 在相同条件下随着车辆行驶速度的增大,路面最大位移量变小,但是最大位移量的变化幅度很小,趋势不是很明显。
(5) 车辆超载后,路面最大位移量增大明显,超载比例达到100%情况下,路面变形增大幅度在50%~109%之间。
(6) 路基强度降低后,路面最大位移量明显增大,路基强度降低28%后,路面变形增大幅度在15%左右。
| [1] |
陈果. 车辆-轨道耦合系统随机振动分析: [D]. 成都: 西南交通大学, 2000. CHEN Guo. Random Vibration Analysis of Vehicle-track Coupling System[D].Chengdu:Southwest Jiaotong University, 2000. http://d.wanfangdata.com.cn/Thesis/Y371176 |
| [2] |
许海亮, 何炼, 何兆才, 等. 考虑路面不平整度因素的车路耦合非线性数值模型的建立[J]. 公路交通科技, 2017, 34(8): 23-28. XU Hai-liang, HE Lian, HE Zhao-cai, et al. A Nonlinear Numerical Model of Vehicle-pavement Coupled System Considering Pavement Roughness[J]. Journal of Highway and Transportation Research and Development, 2017, 34(8): 23-28. |
| [3] |
陈静. 车辆与路面相互作用的基础研究[D]. 长春: 吉林大学, 2002. CHEN Jing. Basic Research on Interaction between Vehicle and Pavement[D].Changchun:Jilin University, 2002. http://d.wanfangdata.com.cn/Thesis/Y451460 |
| [4] |
李皓玉, 杨绍普, 李韶华, 等. 车、路的相互作用下沥青路面动力学特性分析[J]. 振动与冲击, 2009(4): 86-89, 102, 205. LI Hao-yu, YANG Shao-pu, LI Shao-hua, et al. Analysis of Dynamic Characteristics of Asphalt Pavement under the Interaction of Vehicle and Road[J]. Journal of Vibration and Shock, 2009(4): 86-89, 102, 205. |
| [5] |
孙璐, 邓学钧. 速度与车辆动态特性对于车路相互作用的影响[J]. 土木工程学报, 1997, 30(6): 34-40. SUN Lu, DENG Xue-jun. The Influences of Speed and Dynamic Characteristics of Truck on Vehicle-pavement Interactions[J]. China Civil Engineering Journal, 1997, 30(6): 34-40. |
| [6] |
张艳美. 高速公路路基的动力特性研究[D]. 兰州: 兰州铁道学院, 2001. ZHANG Yan-mei. Study on Dynamic Characteristics of Expressway Subgrade[D].Lanzhou:Lanzhou Railway Institute, 2001. |
| [7] |
陈华. 交通荷载作用下公路路基的动力有限元分析[D]. 兰州: 兰州理工大学, 2004. CHEN Hua. Dynamic Finite Element Analysis of Highway Subgrade under Traffic Load[D].Lanzhou:Lanzhou University of Technology, 2004. http://d.wanfangdata.com.cn/Thesis/Y621155 |
| [8] |
银花, 李懿. 车辆-沥青路面耦合系统相互作用研究[J]. 振动与冲击, 2013, 32(20): 107-112. YIN Hua, LI Yi. Interaction in a Vehicle Asphalt Pavement Coupled System[J]. Journal of Vibration and Shock, 2013, 32(20): 107-112. |
| [9] |
许海亮, 袁勇, 屈铁军. 考虑路面不平整度因素的车路耦合振动模型的建立[J]. 振动与冲击, 2014, 33(19): 152-156. XU Hai-liang, YUAN Yong, QU Tie-jun. Dynamic Model for a Vehicle-pavement Coupled System Considering Pavement Roughness[J]. Journal of Vibration and Shock, 2014, 33(19): 152-156. |
| [10] |
陆辉, 孙立军. 轮载作用下沥青路面三维非线性有限元分析[J]. 土木工程学报, 2004, 37(7): 64-67. LU Hui, SUN Li-jun. Analysis on Asphalt Pavement under Tyre Load by Three-dimensional Finite Elment Method[J]. China Civil Engineering Journal, 2004, 37(7): 64-67. |
| [11] |
郝大力, 王秉纲. 路面结构动力响应分析[J]. 长安大学学报:自然科学版, 2002, 22(3): 9-12. HAO Da-li, WANG Bing-gang. Dynamic Response of Pavement Structure[J]. |
| [12] |
朱孔源. 车辆-柔性路面力学相互作用系统的研究[D]. 北京: 中国农业大学, 2001. ZHU Kong-yuan. Research on Vehicle-flexible Pavement Mechanical Interaction System[D].Beijing:China Agricultural University, 2001. http://d.wanfangdata.com.cn/Thesis/Y410467 |
| [13] |
任俊达, 张怀志, 谭忆秋. 基于三维黏弹有限元法的沥青路面结构力学响应分析[J]. 公路交通科技, 2017, 34(1): 15-23. REN Jun-da, ZHANG Huai-zhi, TAN Yi-qiu. Analysis on Mechanical Response of Asphalt Pavement Structure Based on 3D Viscoelastic Finite Element Method[J]. Journal of Highway and Transportation Research and Development, 2017, 34(1): 15-23. |
| [14] |
王亚, 陈思忠, 郑凯锋. 时空相关路面不平度时域模型仿真研究[J]. 振动与冲击, 2013, 32(5): 70-74. WANG Ya, CHEN Si-zhong, ZHENG Kai-feng. Simulation Research on Time Domain Model of Road Roughness with Time-space Correlation[J]. Journal of Vibration and Shock, 2013, 32(5): 70-74. |
| [15] |
王直民, 张土乔, 吴小刚. 不平整路面上的车辆等效动载系数[J]. 浙江大学学报:工学版, 2007, 41(6): 1007-1011. WANG Zhi-min, ZHANG Tu-qiao, WU Xiao-gang. Equivalent Vehicle Dynamic Load Coefficient on Rough Pavement[J]. Journal of Zhejiang University:Engineering Science Edition, 2007, 41(6): 1007-1011. |
| [16] |
邓学钧, 孙璐. 车辆-地面结构系统动力学[M]. 北京: 人民交通出版社, 1998. DENG Xue-jun, SUN Lu. Vehicle-ground Structure System Dynamics[M]. Beijing: China Communications Press, 1998. |
| [17] |
刘云, 钱振东. 路面平整度及车辆振动模型的研究综述[J]. 公路交通科技, 2008, 25(1): 51-57. LIU Yun, QIAN Zhen-dong. Review of Road Roughness and Vehicle Vibration Model[J]. Highway Traffic Science and Technology, 2008, 25(1): 51-57. |
| [18] |
赵济梅. 路面平度谱分析应用研究报告[R]. 长春: 长春汽车研究所整车研究室, 1985. ZHAO Ji-mei. Application of Pavement Flatness Spectrum Analysis[R]. Changchun:Changchun Automobile Research Institute, 1985. |
 2017, Vol. 34
2017, Vol. 34
