扩展功能
文章信息
- 张东, 何亮, 侯曙光, 边疆
- ZHANG Dong, HE Liang, HOU Shu-guang, BIAN Jiang
- 沥青混合料断裂数值模拟进展
- Advance in Numerical Simulation of Asphalt Mixture Fracture
- 公路交通科技, 2017, 34(12): 1-8, 22
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(12): 1-8, 22
- 10.3969/j.issn.1002-0268.2017.12.001
-
文章历史
- 收稿日期: 2016-11-18
2. 南京工业大学 道路工程研究所, 江苏 南京 210009
2. Institute of Road Engineering, Nanjing Tech University, Nanjing Jiangsu 210009, China
截至2015年底,我国公路总里程达到457.73万km,其中高速公路总里程达到12.35万km,居世界第一位。在高等级公路中,以沥青混合料为铺面材料的沥青路面占90%以上。裂缝是沥青路面常见的病害,如图 1所示。裂缝的形成降低了沥青路面的服务水平,减少了沥青路面的使用寿命,增加了沥青路面的养护成本。研究沥青混合料的开裂机理对于深入理解沥青混合料的断裂原因、断裂方式和提高沥青混合料的抗裂性能具有重要意义。数值模拟是研究沥青混合料断裂的有效手段。

|
| 图 1 沥青路面裂缝 Fig. 1 Cracks in asphalt pavement |
| |
如图 2所示,沥青混合料是由粗细集料、沥青和空隙组成的多相、不均质材料。在荷载作用下,裂缝可能在沥青砂浆中、集料颗粒内部或沥青砂浆与集料的界面上形成和扩展。裂缝的最终路径取决于沥青混合料的细观结构、沥青砂浆和集料之间界面的连接强度以及沥青砂浆和集料颗粒的强度。因此,沥青混合料的断裂模式非常复杂。尽管目前断裂力学理论和数值模拟手段取得了很大进步,沥青混合料的断裂模拟问题还处于探索阶段。本研究系统地总结了国内外在沥青混合料断裂模拟方面所做的研究工作和取得的成果。

|
| 图 2 沥青混合料试件剖面 Fig. 2 Profile of asphalt mixture sample |
| |
1 沥青混合料断裂模拟数值方法
目前,用于沥青混合料断裂研究的理论方法主要有3类,即经典断裂力学理论、内聚力模型(cohesive zone model,简称CZM)和损伤力学理论[1-6]。损伤力学理论用于分析材料的疲劳断裂问题。疲劳断裂是断裂领域一个相对独立的分支,本研究不作综述。在经典断裂力学理论中,用于判断裂缝扩展的参数有能量释放率G,强度因子K和J积分。经典断裂力学方法中需要预设一个无限尖的裂缝,这导致了裂缝尖端应力的奇异性。然而,在实际材料中真正奇异的应力是不存在的。当裂缝尖端的应力超过一定程度时,裂纹端点附近会产生局部塑性区。基于此,Dugdale[7]和Barenblatt[8]提出了内聚力模型,用内聚力和张开位移来表征塑性区内材料的本构关系[1, 9]。
在数值模拟中,可以借助有限元方法或离散元方法,利用经典断裂力学理论或内聚力模型研究沥青混合料的断裂问题,以下作分类综述。表 1中列出了各种方法的理论基础、断裂本构关系和优缺点。
| 理论基础 | 断裂本构关系 | 优缺点 | |
| 有限元 方法 | 均质模型 | 应力强度因子/J积分 | 缺点:(1)需要预设裂纹,不适用于分析初始裂缝形成问题,也无法模拟裂缝的扩展过程;(2)没有考虑沥青混合料的不均匀性。 |
| 内聚力模型 | 优点:消除了裂纹尖端的应力奇异性,可以模拟裂缝的形成和扩展过程。 缺点:没有考虑沥青混合料的不均匀性。 | ||
| 细观模型 | 内聚力模型/应力强度因子/J积分 | 优点:在一定程度上考虑了沥青混合料的不均匀性。 主要缺点:(1)二维模型无法真实模拟裂缝的形成和扩展,而采用三维模型存在收敛困难和单元畸变等问题;(2)有限元模型很难引入沥青混合料中的空隙。 | |
| 离散元 方法 | 二维模型 | 内聚力模型/接触粘结模型 | 优点:部分地反映了沥青混合料的细观结构。 缺点:二维模型无法准确研究沥青混合料中裂缝的形成和扩展机理。 |
| 三维模型 | 内聚力模型/接触粘结模型 | 优点:可以真实模拟沥青混合料的空间三维细观结构。 现有研究的局限性:在一定程度上揭示了沥青混合料的断裂特点和断裂过程,但仅限于Ⅰ型断裂问题,对于Ⅱ型裂缝和复合型裂缝的形成和扩展问题还有待研究;并且,在模型构建和细观断裂本构关系选择等方面还有待进一步深入和完善。 | |
2 有限元方法在沥青混合料断裂模拟中的应用 2.1 基于经典断裂力学理论的有限元方法
经典断裂力学理论是研究含裂缝的构件在各种环境下(包括荷载作用、温度变化、湿度变化等)裂缝的平衡、扩展和失稳规律的一门学科。线弹性断裂力学是经典断裂力学理论中最简单和发展比较成熟的一个分支。它以弹性力学的基本理论为基础,将裂纹作为边界条件来处理,通过裂纹体附近的应力场、位移场来分析带裂纹结构的承载能力和抗断裂韧性与裂纹长度之间的定量关系。线弹性断裂力学主要适用于弹脆性材料或准脆性材料,应力强度因子K可以用来分析材料和结构的断裂问题。
运用经典断裂力学理论,通过建立路面结构的有限元模型,很多学者研究了含初始裂缝的面层或基层中应力强度因子的大小和变化规律。罗睿等人[10]应用权函数推导了沥青路面表面裂缝应力强度因子的计算方法。郑健龙等[11]将基层中含有贯穿裂缝的路面简化为二维问题,以应力强度因子作为表征参量,探讨了车辆荷载作用下基层和面层之间加入软弱层对反射裂缝的防治效果。黄志义等人[12]分析了车辆行驶速度、温度和阻尼比对含反射裂缝的沥青路面动应力强度因子分布规律的影响。王宏畅等人[13]采用三维有限元模型研究了路面结构参数对基层裂缝应力强度因子的影响以及应力强度因子在基层裂缝扩展过程中的变化规律。基于经典断裂力学理论的有限元方法需要在模型中预设裂纹,所以不适用于分析初始裂缝的形成问题,也无法模拟裂缝的扩展过程。
2.2 基于内聚力模型的有限元方法CZM将物理断裂局限在内聚力区域内,这个区域是由2个假想的面来定义的,界面上作用有内聚力。Ⅰ型断裂模式下的内聚力模型示意图如图 3所示,tn和δn分别代表法向内聚力和法向位移。裂缝尖端的内聚力为零,内聚力最大的点称为内聚力区域尖端。内聚力区域就是材料裂缝尖端和内聚力区域尖端之间的区域,在这个区域内将产生复杂的断裂行为(包括非线弹性断裂)。假想的面是通过内聚力结合在一起的,而内聚力又取决于2个面的张开位移。外荷载的增加将导致界面张开位移的增加,从而导致内聚力的变化,内聚力先是增加,然后达到最大值,最后减小直到为零。内聚力达到最大值标志着裂缝的开始;内聚力减小为零标志着界面的张开位移达到最大值,此时,材料失效,裂缝形成。

|
| 图 3 内聚力模型示意图 Fig. 3 Schematic diagram of cohesion model |
| |
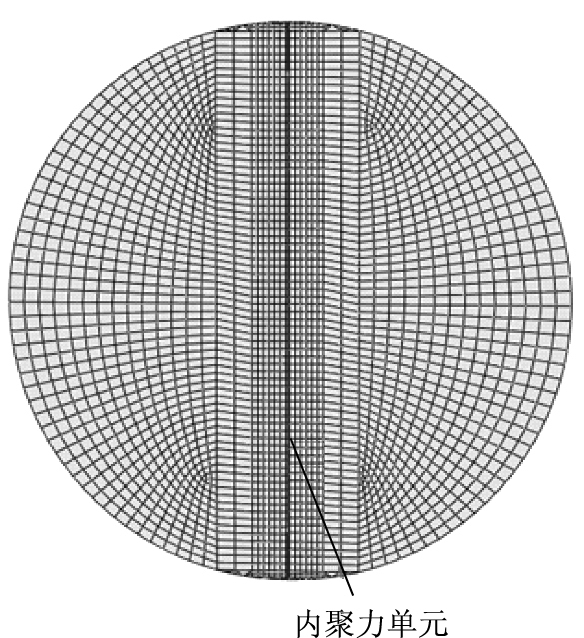
内聚力模型消除了裂纹尖端的应力奇异性问题,并且无需在有限元模型中预设裂缝,从而可以模拟裂缝在材料中的形成和扩展过程。内聚力模型已经被用于研究沥青混合料的断裂问题。在研究中,根据沥青混合料的有限元建模情况,内聚力模型的应用可以分为2类:均质有限元模型和细观有限元模型。均质有限元模型将沥青混合料假定为各向同性的均质材料,在建模时只在预先假定断裂的区域布置内聚力单元,如图 4所示。细观有限元模型将沥青混合料简化为由粗集料和沥青砂浆组成的二相体系,在沥青砂浆以及沥青砂浆与粗集料的界面上布置内聚力单元,如图 5所示。以下内容总结了内聚力模型在均质有限元模型中应用取得的成果。内聚力模型在细观有限元模型中的应用见2.3节。
|
| 图 4 均质有限元模型 Fig. 4 Homogeneous finite element model |
| |

|
| 图 5 细观有限元模型 Fig. 5 Meso-level finite element model |
| |
Jenq和Perng[14]针对沥青混合料提出了一个内聚力模型,而后Jenq等人[15]利用这个模型研究了旧水泥路面加铺沥青罩面层路面结构的低温开裂问题。Paulino等人[16]针对沥青混合料提出了一个内置的内聚力模型,模拟了间接拉伸试验中裂缝的扩展。Song等人[9]使用内置的内聚力模型研究了在荷载作用下单边切口梁(single-edge notched beam,简称SEB)Ⅰ型裂缝和复合裂缝的扩展。Li和Marasteanu[17]使用内聚力模型研究了低温环境下沥青路面的断裂问题。Song等人[18]考虑了沥青混合料的黏弹性,使用双线性内聚力模型研究了沥青混合料的断裂行为,模拟得到的复合型裂缝扩展路径与试验结果具有很好的一致性。张东等人[1, 19-20]使用双线性内聚力模型模拟了沥青混合料的劈裂试验,并研究了沥青路面的低温缩裂问题。
2.3 基于细观结构模型的有限元方法以上研究(2.1~2.2节)都将沥青混合料视为各向同性的均质材料。然而,实际沥青混合料是由集料、沥青和空隙组成的不均质、各向异性材料。基于此,有些学者在研究中考虑了沥青混合料的细观结构,针对粗集料和沥青砂浆赋予不同的力学参数,在沥青砂浆以及沥青砂浆与粗集料的界面处使用断裂本构模型。断裂本构模型可以选择内聚力模型、应力强度因子或J积分。
Aragão等人[21]采用数字图像技术在有限元软件中生成沥青混合料细观结构模型,并在沥青砂浆中布置内聚力单元,模拟了沥青混合料的单轴拉伸试验。汪海年等人[22]通过沥青混合料细观结构有限元模型,使用扩展有限元方法(extended finite element method,简称XFEM)模拟了沥青混合料半圆弯拉试验,研究了裂缝扩展路径和裂缝扩展过程中应力分布特性等断裂行为。Ng和Dai[23]通过椭圆拟合二维粗集料颗粒生成沥青混合料细观有限元模型,使用扩展有限元方法模拟了单边切口梁Ⅰ型断裂和复合型断裂试验以及劈裂试验。尹安毅等人[24-26]使用规则的八边形模拟二维集料颗粒,通过随机算法生成沥青混合料细观有限元模型,研究了拉伸试验和单边切口梁试验中沥青混合料的断裂行为。
上述研究采用的二维细观结构有限元模型在一定程度上考虑了沥青混合料的不均匀性,而且扩展有限元方法可以模拟裂缝的形成和扩展。但是,存在下述问题:
(1) 实际裂缝是在三维空间中形成和扩展的,采用二维模型不能准确模拟裂缝的形成和扩展问题。而如果采用实际沥青混合料三维细观有限元模型,由于粗集料的不规则性,需要划分极细的有限元网格,在引入界面断裂本构关系以后,计算规模巨大,而且计算会因为收敛困难和单元畸变等因素终止[27]。
(2) 实际沥青混合料断裂过程中,粗集料颗粒也会发生断裂,这种情况很难使用有限元方法模拟。在现有的有限元模拟中,裂缝只能在沥青砂浆内部以及粗集料和沥青砂浆之间的界面上形成和扩展。
(3) 实际沥青混合料中存在空隙,空隙对微裂缝的产生和扩展有一定的影响。在有限元模型中,很难引入空隙。因为如果引入随机分布的空隙,将导致网格划分的困难,并且在计算中造成应力集中。
(4) 实际沥青混合料中细观力学参数具有一定的不均匀性,并服从一定的分布,使用有限元方法无法考虑这种参数的不均匀性。
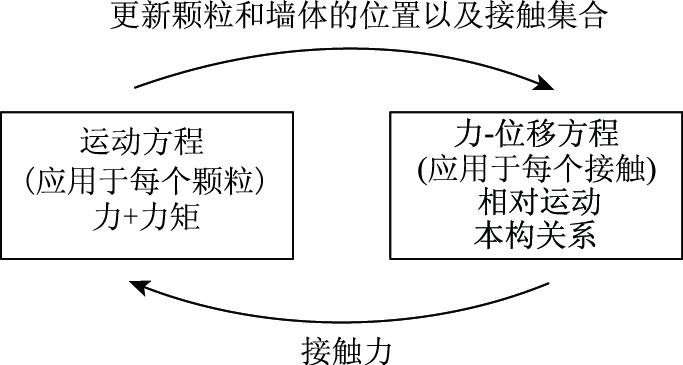
3 离散元方法在沥青混合料断裂模拟中的应用Cundall在1971年提出了离散元方法,用于岩石和岩土材料的研究[28-29]。离散元方法用于模拟由任意形状的颗粒组成的系统的力学行为。颗粒间相互独立,只在接触点处相互作用。颗粒间的受力和运动遵从牛顿第二定律。力-位移方程描述了颗粒间接触处的相对位移和作用在颗粒上的接触力之间的关系。运动方程描述了单个颗粒的平动和转动。离散元计算中,采用计算时步算法(timestepping algorithm),在每个颗粒上反复使用运动方程,在颗粒间的接触处反复使用力-位移方程,并持续更新墙体的位置。计算循环如图 6所示。在每个时间步开始时,更新颗粒之间和颗粒与墙体之间的接触,使用力-位移方程更新接触力;然后,使用运动方程更新颗粒的速度和位置,同时根据指定的墙体速度,更新墙体的位置。
|
| 图 6 计算循环示意图 Fig. 6 Schematic diagram of calculation cycle |
| |
目前,离散元方法被越来越多地用于沥青混合料的研究。使用离散元方法,可以构建包含粗集料、沥青砂浆和空隙的三相体系,从而能真实模拟沥青混合料的细观结构。使用离散元方法模拟沥青混合料断裂问题时,着重解决3个方面的问题:(1)沥青混合料细观结构的重构;(2)细观断裂本构模型和细观断裂参数的确定;(3)断裂行为模拟和结果解释。在细观结构重构方面,主要有2类方法,分别是图像处理法和随机生成算法。沥青砂浆以及沥青砂浆与粗集料之间界面的断裂本构模型有2种,分别是内聚力模型和接触黏结模型。细观断裂参数方面,目前主要是通过宏观试验测试,然后经过反复校正(对比室内试验结果和模拟结果)确定,有待于深入研究。在断裂行为模拟方面,目前有2个趋势:一个是模拟沥青混合料的宏观断裂行为(比如应力-应变关系),另一个是研究沥青混合料的细观断裂行为,比如微裂纹的产生和扩展。以下内容综述现有研究取得的主要成果。
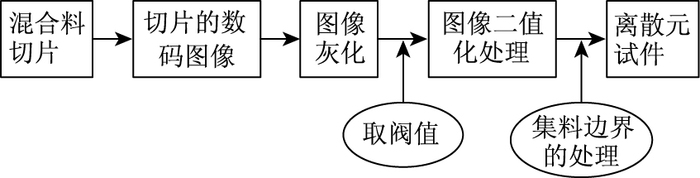
3.1 沥青混合料细观结构离散元建模在二维细观结构模拟方面,通常使用数字图像处理技术在离散元软件PFC2D中生成沥青混合料离散元试件[30-32],技术流程如图 7所示。对于三维细观结构,可以借助X光断层扫描图像技术在离散元软件PFC3D中生成离散元试件[33-34]。基于数字图像的方法,不但耗时而且成本高,需要依赖专门的设备。
|
| 图 7 图像处理法生成离散元试件 Fig. 7 Discrete element sample generated by image processing method |
| |
针对这个问题,侯曙光和张东[35]提出了一种随机生成沥青混合料二维离散元试件的算法。刘玉和张东等人[36-37]提出了一些在PFC3D中随机生成沥青混合料三维离散元试件的算法。生成沥青混合料离散元试件的随机算法包含3个步骤,分别是:粗集料的随机生成算法、沥青砂浆的生成算法和空隙的生成算法。图 8~图 10显示了沥青混合料二维离散元试件的生成过程[35]。

|
| 图 8 粗集料生成 Fig. 8 Coarse aggregate generation |
| |

|
| 图 9 沥青砂浆生成 Fig. 9 Asphalt mastic generation |
| |

|
| 图 10 空隙生成 Fig. 10 Voids generation |
| |
3.2 沥青混合料断裂行为离散元模拟
基于沥青混合料细观结构模型,离散元方法已经被用于研究动态模量和蠕变劲度等宏观力学响应以及模拟实验室试验[30, 31-32, 38-41]。离散元方法也被用于分析沥青混合料的断裂问题。Kim等人[42-44]基于二维细观结构离散元模型,研究了沥青混合料单边切口梁试验中复合型裂缝的扩展、半圆拉伸试验中裂缝的扩展以及半圆拉伸试验中试件的尺寸依赖性。在他们的研究中,裂缝的生成和扩展通过在沥青砂浆内部以及集料和沥青砂浆之间设置双线性内聚力模型实现。张东等人[45]通过随机生成的沥青混合料二维离散元模型,研究了劈裂试验过程中沥青混合料的力学行为、微观断裂模式、裂缝的形成和扩展以及能量消耗问题。
二维细观离散元模型部分地反映了沥青混合料的细观结构。然而,实际沥青混合料中粗集料的分布以及粗集料和沥青砂浆之间的接触关系非常复杂,并且裂缝是在三维空间中生成和扩展。因此,使用二维细观结构模型无法准确研究沥青混合料中裂缝的形成和扩展机理。使用三维离散元方法研究沥青混合料的断裂问题是今后的研究重点,目前已经有一些研究作了初步探索。
陈俊和黄晓明[46]使用三维离散元模型研究了沥青混合料的小梁弯拉试验,研究结果表明模拟得到的梁底应力-应变曲线和试验结果具有较好的一致性。王江洋和钱振东等人[47-48]通过构建三维细观结构离散元模型,研究了环氧沥青混凝土单边切口梁试验中裂缝的形成和扩展。这些研究在一定程度上揭示了沥青混合料的断裂特点和断裂过程。但是,现有的基于三维细观结构的模拟仅限于Ⅰ型断裂问题,对于Ⅱ型裂缝和复合型裂缝的形成和扩展问题还有待研究。并且,在模型构建和细观断裂本构关系选择等方面还有待进一步深入和完善。
4 结论沥青混合料是由集料、沥青砂浆和空隙组成的一种多相复合材料。在荷载作用下,裂缝可能在沥青砂浆内部、沥青砂浆和粗集料之间的界面或者粗集料内部形成和扩展。裂缝的最终扩展路径取决于沥青混合料的细观结构、沥青砂浆和粗集料之间界面的连接强度、沥青砂浆的抗拉强度以及粗集料颗粒的抗拉强度。因此,沥青混合料的断裂模式十分复杂。随着计算机技术的进步和数值模拟手段的发展,国内外在沥青混合料断裂数值模拟方面已经取得了一定成果。从模拟精度来看,基于沥青混合料细观结构的有限元方法和离散元方法是今后值得继续研究的方向。但是,这2类方法都存在一定的局限性和需要进一步解决的问题。具体如下:
(1) 现有基于沥青混合料细观结构的有限元方法局限于二维模型,无法解决裂缝在三维空间中的形成和扩展问题。建议今后进一步研究基于沥青混合料三维细观结构的有限元方法。重点解决如下问题:①考虑粗集料真实形态和分布的三维细观结构有限元模型的构建;②模型网格划分以及引入界面断裂本构关系造成的计算收敛困难和单元畸变问题。
(2) 三维离散元方法可以真实地模拟沥青混合料的细观结构(粗集料、沥青砂浆和空隙),能在最大程度上模拟沥青混合料的细观断裂行为。但是,三维离散元模型计算效率低,计算时间可达数月。因此,如何大幅提高三维离散元方法的计算效率是今后的研究重点。此外,如何准确确定细观断裂本构模型的参数也是需要研究的问题之一。
| [1] |
张东, 黄晓明, 赵永利. 基于内聚力模型的沥青混合料劈裂试验模拟[J]. 东南大学学报:自然科学版, 2010, 40(6): 1276-1281. ZHANG Dong, HUANG Xiao-ming, ZHAO Yong-li. Simulation of Indirect Tension Test of Asphalt Mixtures Based on Cohesive Zone Model[J]. Journal of Southeast University:Natural Science Edition, 2010, 40(6): 1276-1281. |
| [2] |
金光来, 黄晓明, 梁彦龙. 两种不同模式下的沥青混合料断裂过程研究[J]. 湖南大学学报:自然科学版, 2014, 41(6): 120-126. JIN Guang-lai, HUANG Xiao-ming, LIANG Yan-long. A Numerical Analysis of the Fracture Behavior of Asphalt Concrete under Two Different Modes[J]. Journal of Hunan University:Natural Science Edition, 2014, 41(6): 120-126. |
| [3] |
KIM Y R. Mechanistic Fatigue Characterization and Damage Modeling of Asphalt Mixtures[D]. College Station:Texas A&M University, 2003.
|
| [4] |
SI Z, LITTLE K N, LYTTON R L. Characterization of Micro Damage and Healing of AC Mixtures[J]. Journal of Materials in Civil Engineering, 2002, 14(6): 461-470. |
| [5] |
郑健龙. Burgers粘弹性模型在沥青混合料疲劳特性分析中的应用[J]. 长沙交通学院学报, 1995, 11(3): 32-42. ZHENG Jian-long. Application of Burgers Model to the Analysis of Fatigue Characteristic of Bituminous Mixtures[J]. Journal of Changsha Communications University, 1995, 11(3): 32-42. |
| [6] |
徐勋倩, 黄卫, 林广平. 钢桥面沥青铺装层疲劳损伤分析与车辆轴载换算[J]. 东南大学学报:自然科学版, 2005, 35(6): 931-934. XU Xun-qian, HUANG Wei, LIN Guang-ping. Fatigue Fracture Analysis and Axle Load Conversion for Steel Bridge Asphalt Mixture Surfacing[J]. Journal of Southeast University:Natural Science Edition, 2005, 35(6): 931-934. |
| [7] |
DUGDALE D S. Yielding of Steel Sheets Containing Slits[J]. Journal of Mechanics and Physics of Solids, 1960, 8(2): 100-104. |
| [8] |
BARENBLATT G I. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture[J]. Advances in Applied Mechanics, 1962, 7: 55-129. |
| [9] |
SONG S H, PAULINO G H, BUTTLAR W G. Simulation of Crack Propagation in Asphalt Concrete Using an Intrinsic Cohesive Zone Model[J]. Journal of Engineering Mechanics, 2006, 132(11): 1215-1223. |
| [10] |
罗睿, 黄晓明. 沥青路面表面裂缝应力强度因子计算方法研究[J]. 公路交通科技, 2002, 19(1): 13-15. LUO Rui, HUANG Xiao-ming. Research on the Method to Calculate the Stress Intensity Factor of Asphalt Pavement's Edge Crack[J]. Journal of Highway and Transportation Research and Development, 2002, 19(1): 13-15. |
| [11] |
郑健龙, 张起森. 半刚性路面反射裂缝及其应力强度因子的有限元分析[J]. 岩土工程学报, 1990, 12(3): 22-26. ZHENG Jian-long, ZHANG Qi-sen. Finite Element Analysis of Reflective Crack and Stress Intensity Factors in Half Rigid Pavements[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(3): 22-26. |
| [12] |
黄志义, 王金昌, 朱向荣. 动荷载下含反射裂缝沥青路面结构黏弹性分析[J]. 浙江大学学报:工学版, 2007, 41(1): 114-119. HUANG Zhi-yi, WANG Jin-chang, ZHU Xiang-rong. Viscoelastic Analysis of Asphalt Pavement with Reflective Cracks and Subjected to Dynamic Loading[J]. Journal of Zhejiang University:Engineering Science Edition, 2007, 41(1): 114-119. |
| [13] |
王宏畅, 黄晓明. 高等级沥青路面基层底裂缝三维数值分析[J]. 公路交通科技, 2005, 22(12): 1-4. WANG Hong-chang, HUANG Xiao-ming. Three-dimensional Numerical Analysis for Crack at Bottom of Asphalt Pavement Base Course[J]. Journal of Highway and Transportation Research and Development, 2005, 22(12): 1-4. |
| [14] |
JENQ Y S, PERNG J D. Analysis of Crack Propagation in Asphalt Concrete Using Cohesive Crack Model[J]. Transportation Research Record, 1991, 1317: 90-99. |
| [15] |
JENQ Y S, LIAW C J, LIU P. Analysis of Crack Resistance of Asphalt Concrete Overlays:A Fracture Mechanics Approach[J]. Transportation Research Record, 1993, 1388: 160-166. |
| [16] |
PAULINO G H, SONG S H, BUTTLAR W G. Cohesive Zone Modeling of Fracture in Asphalt Concrete[C]//Proceedings of the Fifth International RILEM Conference on Cracking in Pavements:Mitigation, Risk Assessment and Prevention. Limoges, France:RILEM Publications S.A.R.L., 2004.
|
| [17] |
LI X, MARASTEANU M O. Cohesive Modeling of Fracture in Asphalt Mixtures at Low Temperatures[J]. International Journal of Fracture, 2005, 136(1/2/3/4): 285-308. |
| [18] |
SONG S H, PAULINO G H, BUTTLAR W G. A Bilinear Cohesive Zone Model Tailored for Fracture of Asphalt Concrete Considering Viscoelastic Bulk Material[J]. Engineering Fracture Mechanics, 2006, 73(18): 2829-2848. |
| [19] |
张东. 基于内聚力模型的沥青路面断裂研究[D]. 南京: 东南大学, 2010. ZHANG Dong. Research on Fracture of Asphalt Pavement Based on Cohesion Model[D]. Nanjing:Southeast University, 2010. http://d.wanfangdata.com.cn/Thesis/Y1753624 |
| [20] |
赵永利, 张东. 基于内聚力模型的沥青路面低温缩裂研究[J]. 公路交通科技, 2010, 27(1): 11-16. ZHAO Yong-li, ZHANG Dong. Study of Low Temperature Cracking of Asphalt Pavement Based on Cohesive Zone Model[J]. Journal of Highway and Transportation Research and Development, 2010, 27(1): 11-16. |
| [21] |
ARAGÃO F T S, KIM Y R, LEE J, et al. Micromechanical Model for Heterogeneous Asphalt Concrete Mixtures Subjected to Fracture Failure[J]. Journal of Materials in Civil Engineering, 2011, 23(1): 30-38. |
| [22] |
WANG H, ZHANG C, YANG L, et al. Study on the Rubber-modified Asphalt Mixtures' Cracking Propagation Using the Extended Finite Element Method[J]. Construction and Building Materials, 2013, 47: 223-230. |
| [23] |
NG K, DAI Q. Investigation of Fracture Behavior of Heterogeneous Infrastructure Materials with Extended-finite-element Method and Image Analysis[J]. Journal of Materials in Civil Engineering, 2011, 23(12): 1662-1671. |
| [24] |
YIN A, YANG X, ZENG G, et al. Fracture Simulation of Pre-cracked Heterogeneous Asphalt Mixture Beam with Movable Three-point Bending Load[J]. Construction and Building Materials, 2014, 65(13): 232-242. |
| [25] |
YIN A, YANG X, GAO H, et al. Tensile Fracture Simulation of Random Heterogeneous Asphalt Mixture with Cohesive Crack Model[J]. Engineering Fracture Mechanics, 2012, 92: 40-50. |
| [26] |
ZENG G, YANG X, YIN A, et al. Simulation of Damage Evolution and Crack Propagation in Three-point Bending Pre-cracked Asphalt Mixture Beam[J]. Construction and Building Materials, 2014, 55(3): 323-332. |
| [27] |
尹安毅. 沥青混合料开裂破坏行为的细观尺度模拟[D]. 武汉: 华中科技大学, 2013. YIN An-yi. Mesoscale Fracture Simulation of Asphalt Mixture[D]. Wuhan:Huazhong University of Science and Technology, 2013. http://d.wanfangdata.com.cn/Thesis/D409274 |
| [28] |
CUNDALL P A. A Computer Model for Simulating Progressive Large-scale Movements in Blocky Rock Systems[C]//Proceedings of the International Symposium on Rock Fracture. Nancy, France:International Society of Rock Mechanics, 1971:8-11.
|
| [29] |
CUNDALL P A, STRACK O D L. A Discrete Numerical Model for Granular Assemblies[J]. Géotechnique, 1979, 29(1): 47-65. |
| [30] |
ABBAS A, MASAD E, PAPAGIANNAKIS T, et al. Micro-mechanical Modeling of the Viscoelastic Behavior of Asphalt Mixtures Using the Discrete-element Method[J]. International Journal of Geomechanics, 2007, 7(2): 131-139. |
| [31] |
BUTTLAR W G, YOU Z. Discrete Element Modeling of Asphalt Concrete:Microfabric Approach[J]. Transportation Research Record, 2001, 1757: 111-118. |
| [32] |
YOU Z, BUTTLAR W G. Discrete Element Modeling to Predict the Modulus of Asphalt Concrete Mixtures[J]. Journal of Materials in Civil Engineering, 2004, 16(2): 140-146. |
| [33] |
WANG L B, FROST J D, LAI J S. Three-dimensional Digital Representation of Granular Material Microstructure from X-ray Tomography Imaging[J]. Journal of Computing in Civil Engineering, 2004, 18(1): 28-35. |
| [34] |
ADHIKARI S, YOU Z. 3D Microstructural Models for Asphalt Mixtures Using X-ray Computed Tomography Images[J]. International Journal of Pavement Research and Technology, 2008, 1(3): 94-99. |
| [35] |
HOU S, ZHANG D. Generation of the Two-dimensional Discrete Element Sample of Asphalt Mixtures[J]. Journal of Testing and Evaluation, 2016, 44(1): 692-698. |
| [36] |
LIU Y, YOU Z. Visualization and Simulation of Asphalt Concrete with Randomly Generated Three-dimensional Models[J]. Journal of Computing in Civil Engineering, 2009, 23(6): 340-347. |
| [37] |
ZHANG D, HUANG X, ZHAO Y. Algorithms for Generating Three-dimensional Aggregates and Asphalt Mixture Samples by the Discrete Element Method[J]. Journal of Computing in Civil Engineering, 2013, 27(2): 111-117. |
| [38] |
DAI Q, YOU Z. Prediction of Creep Stiffness of Asphalt Mixture with Micromechanical Finite-element and Discrete-element Models[J]. Journal of Engineering Mechanics, 2007, 133(2): 163-173. |
| [39] |
CAI W, MCDOWELL G R, AIREY G D. Discrete Element Modeling of Uniaxial Constant Strain Rate Tests on Asphalt Mixtures[J]. Granular Matter, 2013, 15(2): 163-174. |
| [40] |
杨军, 张旭, 朱浩然. 沥青混合料三轴剪切试验的离散元模拟研究[J]. 建筑材料学报, 2012, 15(1): 64-68. YANG Jun, ZHANG Xu, ZHU Hao-ran. Discrete Element Simulation on Tri-axial Shear Test of Asphalt Mixtures[J]. Journal of Building Materials, 2012, 15(1): 64-68. |
| [41] |
张德育, 黄晓明, 高英. 沥青混合料三维离散元虚拟单轴蠕变试验[J]. 华南理工大学学报:自然科学版, 2012, 40(7): 15-20. ZHANG De-yu, HUANG Xiao-ming, GAO Ying. Three-dimension Virtual Uniaxial Creep Test of Asphalt Mixture by Using Discrete Element Method[J]. Journal of South China University of Technology:Natural Science Edition, 2012, 40(7): 15-20. |
| [42] |
KIM H, WAGONER M P, BUTTLAR W G. Micromechanical Fracture Modeling of Asphalt Concrete Using a Single-edge Notched Beam Test[J]. Materials and Structures, 2009, 42(5): 677-689. |
| [43] |
KIM H, WAGONER M P, BUTTLAR W G. Numerical Fracture Analysis on the Specimen Size Dependency of Asphalt Concrete Using a Cohesive Softening Model[J]. Construction and Building Materials, 2009, 23(5): 2112-2120. |
| [44] |
KIM H, WAGONER M P, BUTTLAR W G. Simulation of Fracture Behavior in Asphalt Concrete Using a Heterogeneous Cohesive Zone Discrete Element Model[J]. Journal of Materials in Civil Engineering, 2008, 20(8): 552-563. |
| [45] |
ZHANG D, HOU S, BIAN J, et al. Investigation of the Micro-cracking Behavior of Asphalt Mixtures in the Indirect Tensile Test[J]. Engineering Fracture Mechanics, 2016, 163: 416-425. |
| [46] |
陈俊, 黄晓明. 基于三维离散元法的沥青混合料断裂过程模拟[J]. 华南理工大学学报:自然科学版, 2012, 40(7): 21-26. CHEN Jun, HUANG Xiao-ming. Simulation of Fracture Process of Asphalt Mixture Using Three-dimension Discrete Element Method[J]. Journal of South China University of Technology:Natural Science Edition, 2012, 40(7): 21-26. |
| [47] |
王江洋, 钱振东, WANGLin-bing. 环氧沥青混凝土裂纹发展的三维可视化离散元模拟[J]. 湖南大学学报:自然科学版, 2014, 41(6): 112-119. WANG Jiang-yang, QIAN Zhen-dong, WANG Lin-bing. Three-dimensional Visualization Discrete Element Modeling of the Crack Development of Epoxy Asphalt Concrete[J]. Journal of Hunan University:Natural Science Edition, 2014, 41(6): 112-119. |
| [48] |
王江洋. 细观尺度下钢桥面铺装用环氧沥青混凝土断裂行为研究[D]. 南京: 东南大学, 2013. WANG Jiang-yang. Research on Fracture Behavior of Epoxy Asphalt Concrete Used for Steel Bridge Wearing Course under Meso-scale[D]. Nanjing:Southeast University, 2013. http://d.wanfangdata.com.cn/Thesis/Y2511321 |
 2017, Vol. 34
2017, Vol. 34
