扩展功能
文章信息
- 徐里, 丁炜, 施进, 张海林, 胡小兵
- XU Li, DING Wei, SHI Jin, ZHANG Hai-lin, HU Xiao-bing
- 带动态障碍区的自由区域路径实时优化问题的混合算法
- A Hybrid Algorithm for Real-time Optimization of Path in Free Area with Dynamic Obstacle Area
- 公路交通科技, 2017, 34(11): 116-125
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(11): 116-125
- 10.3969/j.issn.1002-0268.2017.11.017
-
文章历史
- 收稿日期: 2015-10-19
2. 浙江省标准化研究院, 浙江 杭州 310006;
3. 交通运输部公路科学研究院, 北京 100088;
4. 北京师范大学 减灾与应急管理研究院, 北京 100875
2. Zhejiang Institute of Standardization, Hangzhou Zhejiang 310006, China;
3. Research Institute of Highway, Ministry of Transport, Beijing 100088, China;
4. School of Disaster Reduction and Emergence Management, Beijing Normal University, Beijing 100875, China
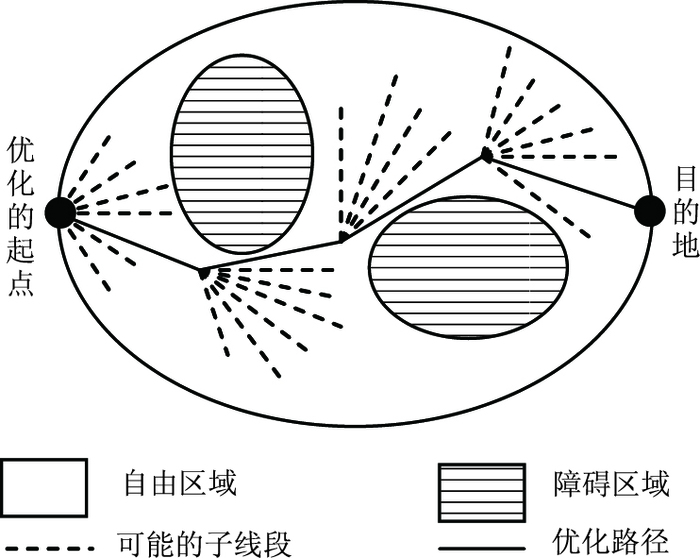
路径优化和障碍规避是交通研究领域里的两个重要问题[1-6]。传统的路径优化问题通常都是基于特定的路径网络进行求解[1-2],而路径网络一般是基于有限数目的节点和联结节点的有限链接来定义的。有了节点和节点间的链接,路径优化的目的就是找出一组节点和链接的子集,从而连通给定的起点和终点,并使得给定的路径指标最优化。自由区域路径优化问题则不同,因为在自由区域路径优化问题中不存在路径网络,而是可以在除障碍区之外的整个区域内自由规划路径(因而可以视为有无穷多的节点和链接)。障碍区可以是固定于某位置的障碍物,也可以是动态变化的特殊区域,例如台风区域、其他运动物体等等。因此,自由区域路径优化问题通常要求针对动态障碍区进行实时路径优化。带动态障碍区的自由区域路径优化问题具有十分广泛的应用背景,例如,民航航空的自由飞计划中的飞机航线优化,航海船舶在公海上的航行路线规划,以及机器人在开放式工作区域中的行走路径优化。飞机在自由飞过程中,需要根据雷电区域、军管区域及其他飞机的位置等障碍区信息进行实时的飞行航线优化。船舶在公海自由航行时,需要根据暗礁区域、台风区域、及其他船舶的位置等障碍区信息进行实时的航路规划。机器人在自由行走时,则需要根据开放式工作区域中的固定障碍物和其他运动物体的位置信息进行实时的路线优化。
与基于路径网络的传统的路径优化问题相比,自由区域路径优化问题在安全、容量、灵活性以及高效性方面都具有显著的优势。例如,现有的空中交通系统可以看作一个基于地面导航站点的航路网络系统,已经越来越难以应对日益增长的空中交通流量[3-5]。因此,民航研究领域提出了“自由飞(Free Flight)”的理念[3-5],就是要彻底摒弃目前结构化的航路网络系统,以实现飞机在整个空域中按需要自主、灵活地规划飞行路线的目的。图 1展示了基于结构化网络的路径优化问题与自由区域路径优化问题的区别。显而易见,结构化的路径网络很可能受到灾害等因素的影响而失效,而基于自由区域的路径规划则具有很好的可靠性和性能。

|
| 图 1 结构化网络与自由区域路径优化问题的区别 Fig. 1 Difference between structured network and free area path optimization problem |
| |
目前国内外学者已开展了许多关于自由区域路径优化问题的研究。例如,在自由飞环境下,如何进行在安全和效率方面的飞行轨迹优化。这类研究的重点主要放在冲突的检测和解决上,提出了几何方法[7]、混合整数线性规划[8]、令牌分配策略[9]、半定规划松弛方法[10]、线性矩阵不等式[11]和遗传算法(GA)[12]。然而,这些关于冲突检测和解决的研究成果都是针对优化飞行路线和飞行安全的短期飞行路线策略,并不适用于长期飞行轨迹的优化。对于长期飞行轨迹优化研究,文献[13]验证了最优飞行路径的可行性,文献[14-15]提出了一种离线的组合函数和参数优化算以分析自由飞的理论效用。文献[16]提出了一种基于整数线性规划模型的启发式集成精确算法以计算起飞时间、飞行路线和速度,以便更好预测到达目的地机场的时间。文献[17]提出了一种改进的遗传算法,该算法考虑到了飞机在自由飞环境中的动态不可用地区以及几种飞行成本。然而,所有这些算法和方法都很难保证在动态环境中的时效性和稳定运行。
本研究提出一种结合遗传算法与滑动地平线控制(RHC)策略的新型算法。RHC策略又称为模型预测控制(MPC),专门用于解决在动态环境下的实时优化问题。简单地讲,RHC策略是提前N步进行的在线优化策略。在每个时间间隔起点,基于当前的可用信息,RHC策略优化接下来最近的N段时间间隔的路径,同时只执行当前的一个时间间隔的优化路径。到下一个时间间隔,RHC将基于更新的信息,重复计算接下来的N段时间间隔的优化路径,以此类推。RHC策略现在已经被控制工程领域广泛接受,与其他控制方法相比,RHC策略具有许多优点[18]。最近,RHC策略在运筹学领域的应用研究也受到了很多重视。例如,文献[19]讨论了关于将RHC策略应用于各类离散事件系统的理论研究工作。文献[20]总结了许多RHC策略在管理学领域的应用研究。文献[21]尝试了应用RHC策略进行有效的动态实时飞机进近排序研究。
本研究则要将RHC策略应用到带动态障碍区的自由区域路径实时优化问题。使用RHC策略的主要目的是:改善实时性,并保证动态环境下的求解性能。为此目的,需要对RHC策略中的重要参数,即滑动地平线的长度和性能指标中的终端加权,进行专门研究。余下部分安排如下:第1节表述了一个带动态障碍区的自由区域路径实时优化问题的数学模型;第2节给出了遗传算法加RHC策略的混合算法的细节;第3节通过模拟试验证实此算法的有效性;第4节为本研究结论。
1 带动态障碍区的自由区域路径实时优化问题 1.1 可选自由路径在自由区域路径优化问题中,有无数可选的自由路径。因此,有必要合理并适当地简化初始问题。使用传统的结构化的路径网络就是简化此问题的一个简单方式。为了能充分利用好自由区域,我们可定义一个有限的可选方向的集合,并引入“时间段”概念,以此将自由区域转换成一个动态路径网络。这样就可以实现在简化问题和使用的恰当算法找到的最优方案之间来进行合理的折中。
使用一个有限的数值的集合来代表可选路径方向,以代替原来的无限的路径方向的集合,是离散化自由区域的关键技术之一。本文中,有限的可选路径方向集合假定如下
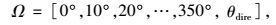
|
(1) |
式中θdire表示从当前位置点到终点的直接方向。所以每次需要确定路径方向时,仅有37个值可供选用。
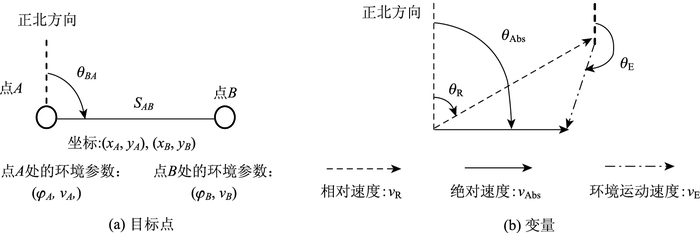
关于“时间段”的概念,我们假设有一个信息发布系统将周期性地发布自由区域内的环境数据,即动态障碍区数据,这个周期叫“时间段”。每个运动体都使用最新更新的信息以便在下一个时间段开始来优化剩余的旅行路径。一个可选的旅行路径包括一系列和时间段相关的子线段。用于当前时间段的子线段是由之前的优化来决定的。图 2示例了实时离散化自由区域路径规划的过程。
|
| 图 2 离散化自由区域路径规划 Fig. 2 Discretized free area path planning |
| |
如果时间段太长,而在Ω中的可选路径方向太少,则离散化后的动态路径网络可能和传统的结构化的路径网络类似,从而几乎无法包括全局最优的路径。另一方面,如果时间段太短,而可选路径方向太多,将会有许多可选的旅行路径,从而导致找到最优方案的计算时间大大增加,实时执行可能性就大大降低了。
1.2 路径优化的性能指标如1.1节所述,一个可选的旅行路径包括一系列和时间段相关的子线段。每个子线段(可选旅行路径的最后一个子线段除外)的旅行时间都可以被看做一个时间段的长度。然后,可选旅行路径的总旅行时间由其所包括的子航线的数值来决定。因此,虽然指标是总旅行时间,但现在优化的基本变量是子航线起始点和终点的坐标。这些基本变量和一些重要参数如图 3所示,(x, y)是一个点的坐标,SAB是A和B两点的距离,(φ, v)是一个点的环境运动方向和速度(如航空中的气流,航海中的洋流),θ表示方向(为更好地与潜在的实际应用结合,文中所有方向都是相对于正北方向而定义的。严格讲,计算一个子线段的终点坐标,即(xB, yB),是不可能的,因为(xB, yB)和(φB, vB)互为前提条件。但是,如果时间段定义得足够短,通常可以假设子线段终点处的环境运动参数与起始点处一致,即(φB, vB)=(φA, vA)。根据此假设,计算(xB, yB)就不再需要(φB, vB)。
|
| 图 3 计算物体运动的一些重要参数 Fig. 3 Key parameters for calculating object movement |
| |
一条子线段的终点坐标(xB, yB),可通过如下计算:
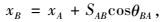
|
(2) |
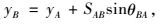
|
(3) |
式中:
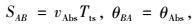
|
(4) |
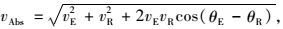
|
(5) |

|
(6) |
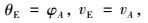
|
(7) |
式中Tts是一个时间段的长度。坐标(xB, yB)随后将被用于下个子线段的起始点。然后,基于相关信息服务部门发布的环境运动参数,新子线段的终点坐标也可通过相同的方式进行计算。子线段的计算可以一直进行到到达目标地为止。
对于一个可选旅行路径的最后的子线段,其终点就是目的地,因此,(xB, yB)是已知的,不再需要按式(1)和(2)计算。但是,最后子线段的旅行时间一般不再等于一个时间段的长度,而是需要进行计算。假定图 3中的B点就是目的地,则最后子线段的旅行时间可以通过如下计算:
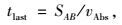
|
(8) |
式中:
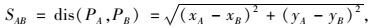
|
(9) |
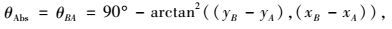
|
(10) |
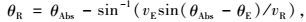
|
(11) |
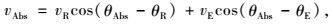
|
(12) |
而“arctan2(·)”是计算四象限反正切的函数。
假设,排除最后的子线段,在一条可选旅行路径里有N条子线段。那相应的旅行时间成本为:
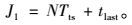
|
(13) |
应用于自由区域路径实时优化问题的现存方法有一个共同点,即在每一个时间段,优化的对象都是从当前子线段的结束点到目的地的剩余旅行路径。因此,这些方法总会面临两个常见问题。一个问题是,在带动态障碍区的自由区域中,要在一个很短的时间段内完成对于长途旅行的路径优化,通常很难实现。另一个问题是,在动态环境中,由于未来不确定信息的原因,从目的地反推到当前子线段结束点的优化方法所计算出的优化路径,其性能和可靠性都会大大降低。例如,文献[14]中所述,近期优化路径的选择是由基于更不可靠信息计算出来的未来优化路径来决定的,这显然是不合理的。
2.1 RHC策略本研究提出使用滑动地平线(RHC)策略来克服现存方法中的上述问题。在每个阶段,即在每个时间段,RHC策略将只优化近期N个时间段内的旅行路径。这样,无论到目的地旅行距离有多远,每次在线优化所需的计算时间都有一个上限,这个计算时间的上限主要取决于N,即滑动地平线的长度。而且,适当地选择滑动地平线的长度能像过滤器一样滤除未来的不可靠信息。图 4直观地显示了RHC策略以及其相对于传统全路径动态优化策略的潜在优势。
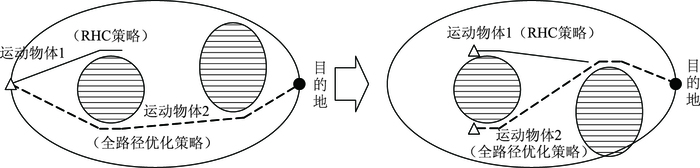
|
| 图 4 RHC策略与传统全路径动态优化策略比较 Fig. 4 Comparison between RHC strategy and traditional full path dynamic optimization strategy |
| |
式(13)中所定义的J1是根据传统全路径动态优化策略而设计的优化性能指标。对于RHC策略,在每个时间段,仅需优化滑动地平线内的旅行路径,这只与N的大小有关,而与到目的地的距离无关。因此,最小旅行时间看起来对RHC策略没有什么意义。但事实是,在自由区域内,与N个时间段对应的多数可选路径都是Z字型(因为如果每个时间段都可以随机选取方向的话,正如后文中遗传算法的做法,那么所得到的N个时间段的总路径很少可能会是直线路径),这意味着捷径通常存在于Z字型路径的子线段之间,如图 5所示。显然,即使原来计划的可选Z字型路径是基于N个时间段的固定长度的滑动地平线,但走捷径后,除了实际路径长度缩短了,沿捷径从Z字型路径起点到其终点的旅行时间也会缩短,不过具体缩短了多少并不确定。因此,通过找捷径降低基于固定长度的滑动地平线的旅行时间仍是有意义的。事实上为了找到最短旅行路径,传统的全路径动态优化策略也需要找捷径。
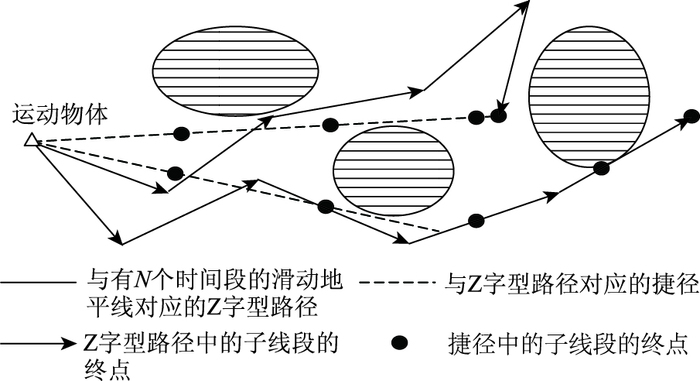
|
| 图 5 N个时间长度的Z字型航线和捷径 Fig. 5 Zigzag route of N-time slice lengths |
| |
假定,在第k个时间段,在走捷径后,原来的可选Z字型路径变为了M(k)个时间段,其中0≤M(k)≤N是一个实数,而M(k)的小数部分等于通过对应捷径上最后一个子线段的旅行时间除以Tts,即有:
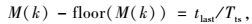
|
(14) |
式中“floor”使M(k)四舍五入向负无穷大就近取整。
这样一来,RHC策略采用的性能指标如下:
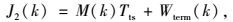
|
(15) |
式中Wterm(k)是一个与最后一条子线段和目的地相关的终端加权函数。稍后我们会提供更多关于Wterm(k)细节的论述。然后,在一个自由区域环境下优化旅行路径的RHC算法可以按如下描述:
步骤1:当运动物体从起点出发,让k=0。
步骤2:接收信息服务机构发布的更新环境数据, 以当前运动物体所在点P(k)作为开始路径优化的起始点, 然后解决如下的最小化问题:
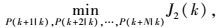
|
(16) |
式中P(k+i|k),i=1, …, N是与第k时刻所对应的滑动地平线的一个可选Z字型路径中的第i子线段的终点,这些点不能位于任何障碍区内。假设最优解为[P*(k+1|k), …, P*(k+N|k)],而相应的捷径为[Pf*(k+1|k), …, Pf*(k+ceil(M(k))|k)],其中“ceil”将M(k)四舍五入向正无穷大就近取整。
步骤3:当飞机到达P(k),设定:
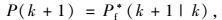
|
(17) |
则运动物体在当前时间段按照[P(k), P(k+1)]所确定的子线段飞行。
步骤4:如果P(k+1)不是目的地,让k=k+1,然后去步骤2。否则,计算结束。
2.2 基于遗传算法(GA)的优化程序第1节里的数学模型提供了离散化的动态路径网络,求解最小化问题, 首先就需要在离散化的动态路径网络中快速高效地找到可行的旅行路径。众所周知,遗传算法(GA)是一个大规模平行随机搜索和优化算法,它能很好地解决最小化问题。例如,文献[17]提出了用GA优化自由飞环境下的全路长飞行路径。本文则要在其基础上,提出适用于自由区域路径实时优化问题的基于RHC策略的GA算法。在GA中的染色体是根据原始的Z字型路径或捷径路径中的子线段端点来构造的。由于M(k)是一个不确定的有限实数,不同的染色体可以有不同的长度。换句话说,本文中的遗传算法采用的是可变长度的染色体设计。因此,一个染色体的构造可以是:第一个基因记录M(k)的值,“ceil(M(k))”是相应旅行路径中子线段端点的数目,而接下来的基因按顺序记录下这些端点的坐标,如图 6所示。

|
| 图 6 GA中的染色体的结构和含义 Fig. 6 Structure and meaning of chromosomes in GA |
| |
基于一个染色体上记录的信息,相应的旅行路径的J2(k)可以根据式(2)到式(15)计算出来。在第k时刻,假定GA中每代群体有N个染色体,第i个染色体的J2(k)值是qi(k),而qmax(k)和qmin(k)表示J2(k)在此代中的最大和最小值。那么,第i个染色体的适应性定义如下:
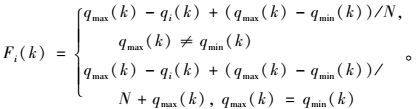
|
(18) |
在文献[18]中,提出了一些改进GA性能的有效技术,如自适应交叉和变异概率,以及启发法规则等。文中的GA将采用这些技术,但限于篇幅原因,不多赘述。
2.3 滑动地平线的长度和终端加权滑动地平线的长度,即N的选择,是至关重要的。RHC策略每轮在线计算时间有一个上限,主要取决于N的大小,通常可以通过模拟进行估计。因此,只要RHC策略中的时间段大于这个计算时间的上限,则无论全程距离有多远,我们总能保证算法的实时有效性。另外,适当地选择滑动地平线的长度,可以像过滤器一样滤除长远未来的不可靠信息。如果N太大,RHC策略将面临和现存的全路长优化方法一样的关于实时计算和动态环境的问题;反之,如果N太小,RHC策略将变得短视,而且性能将极大地降低。因此,需要合理选择N的大小,以使RHC策略在在线计算时间和算法的稳定性能之间得到最好的平衡。
但是,滑动地平线的性质让RHC策略在某种意义上不可避免地变得短视,特别是和静态环境中的传统全路径优化方法相比较时。因此,我们需要精心设计J2(k)中的终端加权Wterm(k),以求能有效降低RHC策略的短视性。
在控制工程领域,无终端加权的RHC策略曾被广泛应用,然而,这种RHC策略经常导致系统变得不稳定。为了解决这个问题,人们专门引进了终端加权的技术[18]。现在,终端加权已成为保证RHC策略的稳定性的一个关键技术。将RHC策略应用于自由区域路径优化问题时,如果没有终端加权或使用了一个不恰当的终端加权,则算法性能将一塌糊涂。
假设Wterm(k)从J2(k)中移除,即:
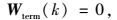
|
(19) |
那么,如果目的地不在第k个时间段的范围内的话,J2(k)将没有目的地的信息。这种情况下,在线优化的结果将导致一个随机的旅行路径,这很可能永远不会指向目的地,如图 7中的虚线所示。这是一个由于在J2(k)中没有终端加权所造成的不稳定情况。
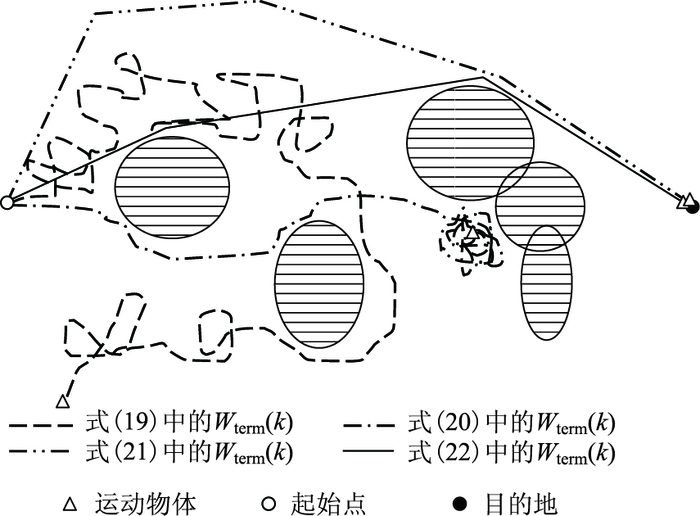
|
| 图 7 各种终端加权的效果 Fig. 7 Effects of different terminal weightings |
| |
将目的地的信息加到J2(k)中的一个简单方法是使用如下的终端加权计算:
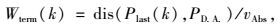
|
(20) |
式中Plast(k)是可选路径中的最后一条子线段的终点,PD.A.是目的地,而地上速率vAbs和函数“dis”在式(9)和式(12)中分别给出了。在式(20)中的Wterm(k)能有效避免由于式(19)而产生的随机旅行航线,并可以在许多条件下让运动物体抵达目的地。但是,式(20)中没有障碍区域的信息,有时会产生一个新的问题,即运动物体被困在一个小区域,RHC算法几乎无法使其离开,如图 7上的点虚线所示。
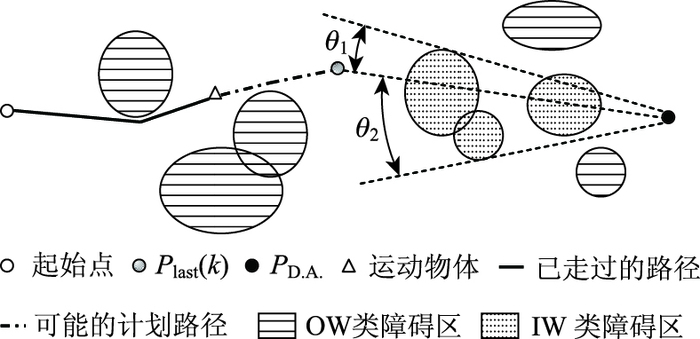
为了避免被困的现象,应在终端加权中加入一些必要的障碍区域的信息。基本上,在PD.A.(目的地)和Plast(k)(可选路径中的最后一条子线段的终点)之间存在的那些障碍区域是导致被困问题的主要原因。出于方便考虑,此后我们将这些在PD.A.和Plast(k)之间的障碍区域叫做IW区域,其他障碍区域叫OW区域。如果没有IW区域,那么Wterm(k)就如式(20)。否则,到Plast(k)最近的IW区域(可能包括相互重叠的一些椭圆形区域)可以用于终端加权计算如下:
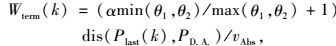
|
(21) |
式中θ1和θ2是显示在图 8上的角度,而α>0是一个系数。使用式(21)中的Wterm(k)能防止运动物体被困在某一区域,因为在潜在的受困区域,min(θ1, θ2)/max(θ1, θ2)接近于1,将导致很大的终端加权函数值。
|
| 图 8 静态环境下第一种终端加权说明 Fig. 8 Illustration of first terminal weighting in static environment |
| |
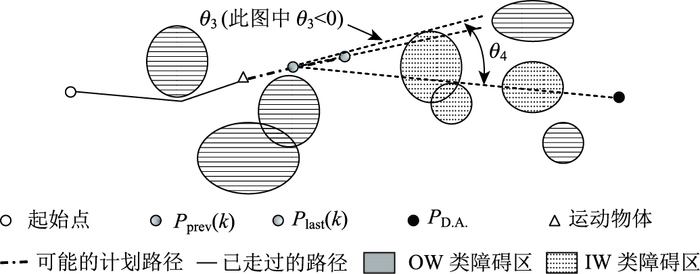
然而,式(21)中的Wterm(k)可能会导致较长的旅行时间。如图 7中的双点虚线所示,为了避免被困,运动物体可能会偏离直接航向θdire很远。为了使RHC算法能更有效地找到最优路径,而不只是可行的路径,需要对终端加权做更多修改。假设Pprev(k)是遵照可选路径的点Plast(k)而延伸出来的点。如果IW区域的数目不为零,那么一个更有效的终端加权为:
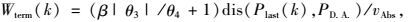
|
(22) |
式中θ3和θ4是图 9所示的角度,而β>0是一个系数。θ3>0表示可选路径中的最后一条子线段在向外偏离目的地。相反,θ3 < 0表示在向内偏离。无论哪种情况,都将按式(22)由Wterm(k)做出惩罚。式(22)的Wterm(k)是一个很有效的定义,其效果如图 7中的实线所示。
|
| 图 9 静态环境下第二种终端加权说明 Fig. 9 Illustration of second terminal weighting in static environment |
| |
在一个动态环境中,障碍区域可能移动,面积形状发生改变或者甚至消失。障碍区域的动态特征也可以简单地包括在Wterm(k)。某种程度上,利用障碍区域的动态特征的一个简单方式就是考虑到Plast(k)最近的IW区域的移动方向:
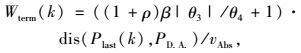
|
(23) |
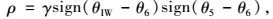
|
(24) |
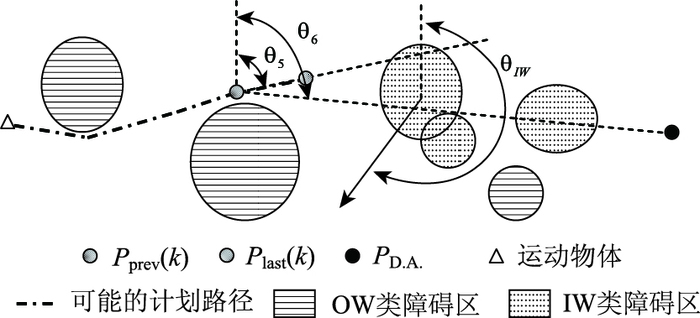
式中θ3和θ4如图 9所示,θ5,θ6和θIW是相对于正北方向的顺时针方向旋转角,如图 10所示,θIW是到Plast(k)最近的IW区域的移动方向,γ>0是一个转向参数,而“sign”是一个符号函数。
|
| 图 10 动态环境下终端加权说明 Fig. 10 Illustration of terminal weighting in dynamic environment |
| |
目前,终端加权计算仅使用了到Plast(k)最近的IW区域信息。关于如何使用其他的障碍区域信息可以进行进一步的研究。例如,结合具体问题中的障碍区域的空间分布特征和动态特性开展研究,但已不在本研究的讨论范围内了。
3 仿真结果为了评估本研究所提出的GA加RHC策略的混合算法,采用民航中的自由飞路径优化问题作为验证案例。文献[17, 22]建立了的一套仿真系统来模拟自由飞行环境,为了对比,特意使用文献[17]中基于GA的传统全路径动态优化算法。为了便于区别,此后使用了RHC策略的混合算法简称为RHC,而文献[17]中的算法为CDO。由于它们都使用了相同的GA作为在线优化算子,因此将RHC和CDO进行对比就很公平。关于GA优化算子的更多细节请见文献[17]。在仿真试验中,除非特别指定,仿真试验中一个时间段是10 min长,滑动地平线的长度为N=6(表 5对应的试验除外,因为表 5专门研究不同N的影响),或1 h长,RHC使用式(23)中定义的终端加权计算Wterm(k)(表 6对应的试验除外,因为表 6专门研究不同终端加权的影响)。
| RHC性能/s | 静态环境 | 动态环境 | |||||
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | ||
| N=1 | OCT | 0.834 0 | 0.936 5 | 1.336 2 | 0.733 7 | 0.846 5 | 1.259 0 |
| AFT | 4 006.5 | 8 054.9 | 17 891.0 | 4 225.1 | 7 976.8 | 16 922.0 | |
| N=3 | OCT | 1.300 3 | 1.950 7 | 2.539 2 | 1.290 7 | 1.461 2 | 2.265 2 |
| AFT | 3 965.0 | 7 811.0 | 15 674.0 | 4 226.5 | 7 482.6 | 16 207.0 | |
| N=6 | OCT | 2.567 5 | 4.849 8 | 7.304 7 | 2.493 0 | 3.841 9 | 7.875 4 |
| AFT | 3 966.2 | 7 421.5 | 14 905.0 | 4 221.6 | 7 454.3 | 15 932.0 | |
| N=9 | OCT | 4.626 4 | 10.601 7 | 18.255 4 | 4.096 6 | 8.575 4 | 17.737 0 |
| AFT | 3 965.9 | 7 407.6 | 14 894.0 | 4 221.9 | 7 462.4 | 16 074.0 | |
| Wterm(k) | 静态环境 | 动态环境 | |||||
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | ||
| 式(20) | OCT | 2.810 2 | 4.912 1 | 7.112 5 | 2.899 4 | 3.845 3 | 9.456 5 |
| AFT | 4 114.9 | 7 435.3 | 15 183.0 | 4 450.9 | 7 496.1 | 16 114.0 | |
| 式(21) | OCT | 2.729 4 | 5.037 6 | 7.355 2 | 2.512 7 | 3.795 2 | 9.114 9 |
| AFT | 3 969.0 | 7 421.8 | 15 042.0 | 4 219.0 | 7 465.3 | 16 089.0 | |
| 式(22) | OCT | 2.789 7 | 5.116 4 | 7.101 6 | 2.535 3 | 3.768 3 | 8.524 0 |
| AFT | 3 966.3 | 7 414.7 | 14 896.0 | 4 227.3 | 7 405.4 | 16 028.0 | |
| 式(23) | OCT | 2.567 5 | 4.849 8 | 7.304 7 | 2.493 0 | 3.841 9 | 7.875 4 |
| AFT | 3 966.2 | 7 421.5 | 14 905.0 | 4 221.6 | 7 454.3 | 15 932.0 | |
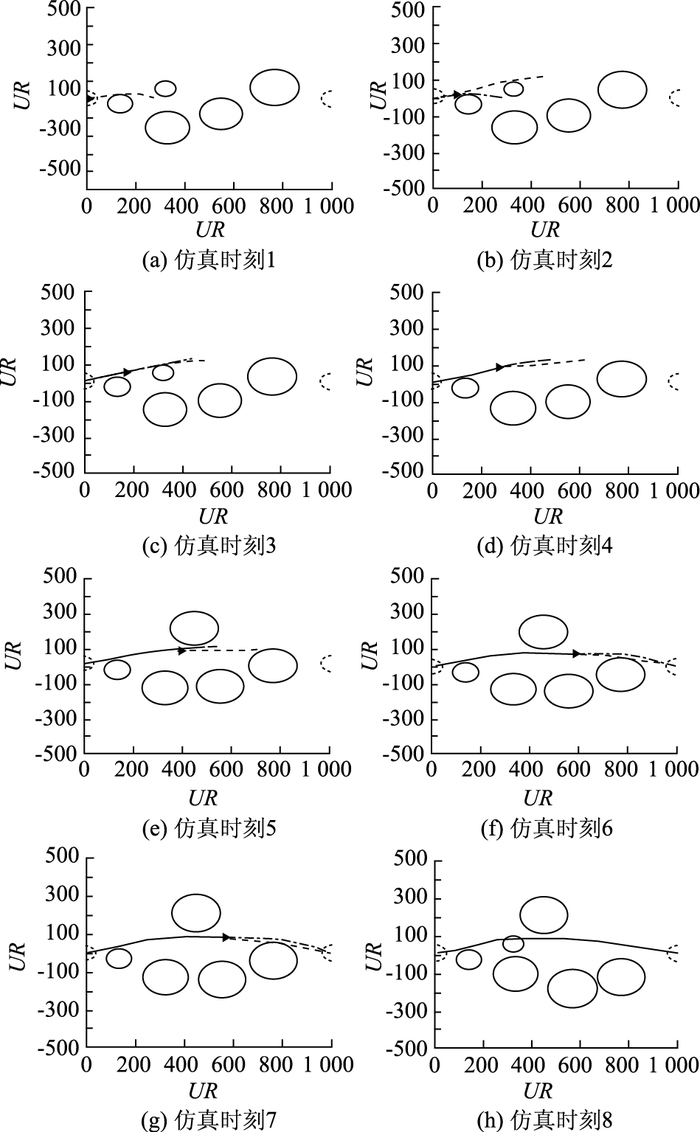
在表 1中定义了6个仿真案例,其自由飞行环境的复杂程度都各不相同,DD表示从始发机场到目的地机场的直接距离,UR表示障碍区域。在案例1~3中,UR是静态的,而在案例4~6中,其随着时间而产生变化,换言之,他们可以移动,面积可以发生改变,消失或可能随机出现新的UR。此仿真主要用于比较RHC和CDO的在线计算时间(OCT)及性能,即从始发机场到目的地机场的实际飞行时间(AFT)。图 11提供了案例5的例子来证明RHC下优化自由飞行路径的动态过程。在图 11中,实圈表示障碍空域,虚圈表示始发/目的地机场,三角表示需要优化自由飞行路径的飞机,虚线是是目前的优化路径,点划线是之前时间段所计算的优化路径,实线是飞机过去的飞行航线。由于篇幅限制,我们仅采用并显示了整个飞行过程中8个飞行时刻相关的结果如图 11的(a)~(h)所示。数值仿真结果见表 2~表 6,其中对于每个静态案例,RHC或CDO进行了10次仿真模拟,而对于每个动态方案则进行了200次仿真模拟。
|
| 图 11 RHC仿真案例(单位:kN) Fig. 11 An example of RHC simulation(unit:kN) 备注:横纵坐标代表飞行空域的范围。 |
| |
| 静态环境 | 动态环境 | |||||
| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | |
| DD/nm | 500 | 1 000 | 2 000 | 500 | 1 000 | 2 000 |
| UR的数目 | 1 | 6 | 14 | 1 | 6 | 14 |
| 单位/s | CDO | RHC | ||||
| Case 1 | Case 2 | Case 3 | Case 1 | Case 2 | Case 3 | |
| 平均OCT | 1.268 7 | 8.367 5 | 77.536 4 | 2.567 5 | 4.849 8 | 7.304 7 |
| 平均AFT | 3 965.6 | 7 407.3 | 14 868.0 | 3 966.2 | 7 421.5 | 14 905.0 |
| 最大OCT | 5.397 0 | 37.479 0 | 364.924 0 | 5.797 0 | 7.408 0 | 15.551 0 |
| 最大AFT | 3 966.9 | 7 435.7 | 14 913.0 | 3 968.7 | 7 480.4 | 15 052.0 |
| 单位/s | CDO | RHC | ||||
| Case 1 | Case 2 | Case 3 | Case 1 | Case 2 | Case 3 | |
| 平均OCT | 0.962 3 | 9.448 5 | 68.921 9 | 2.493 0 | 3.841 9 | 7.875 4 |
| 平均AFT | 4 222.0 | 7 475.6 | 16 192.0 | 4 221.6 | 7 454.3 | 15 932.0 |
| 最大OCT | 5.317 0 | 38.968 0 | 347.915 0 | 5.899 0 | 6.319 0 | 17.694 0 |
| 最大AFT | 4 223.9 | 8 492.5 | 16 638.0 | 4 223.1 | 7 995.8 | 16 118.0 |
| OCT/s | DD=500 nm | DD=1 000 nm | DD=2 000 nm | |||
| Ave. | Max. | Ave. | Max. | Ave. | Max. | |
| 1个UR | 2.493 0 | 5.899 0 | 3.009 8 | 6.469 0 | 3.103 1 | 8.882 0 |
| 6个UR | 3.937 1 | 6.819 0 | 3.841 9 | 6.319 0 | 3.758 0 | 7.030 0 |
| 14个UR | 5.520 0 | 10.765 0 | 5.125 6 | 10.554 0 | 7.875 4 | 17.694 0 |
虽然RHC主要应用于动态方案,但在静态方案中它也需要能正常运转。表 2给出了根据不同算法案例1~3的仿真模拟结果,从中可以看出,在所有3个案例中CDO实现了最好的优化性能,即取得了最小的AFT。这是因为从理论上说,在静态案例中像CDO这样的传统动态全路径优化策略本就应该达到最好的性能。表 2也显示了RHC的性能非常接近CDO,这表示RHC在静态案例中的运行效果不错。关于OCT,RHC很显然比CDO更有效率。由于一个时间段是10 min长,我们可以看出RHC在实时运行方面应该没有问题,而在一些案例中CDO却很难实现在线运行。
我们主要的关注点是动态案例,相关的仿真模拟结果见表 3。在性能方面,对于像案例4和5这样相对简单的案例,CDO和RHC有类似的OCT,而像案例6这样复杂的案例,RHC的性能要比CDO要好。原因已在第1节和第2节中详细阐述过了。因此,RHC能提供比CDO更加可靠的实时运算性能。
案例6是所有6个案例中最复杂的,但DD仅有2 000 nm,和洲际飞行相比仍是非常短的。这表示CDO不可能处理洲际飞行的实时性问题。那RHC呢?在案例6中它的OCT也增加了吗?如表 1所示,从案例4(1)到6(3),DD和UR的数值都增加了。那么是DD还是UR的数值更能影响RHC的OCT呢?表 4回答了这个问题,其中DD在[500, 1 000, 2 000]之间变更,UR数值在[1, 6, 14]之间变更,而所有案例都是动态的。从表 4中可以看出,RHC的OCT主要取决于UR(因为UR的动目极大地影响了寻找可选飞行路径和计算终端加权的GA优化算子的计算负荷),和DD关系不大(因为,对于RHC,不是由DD而是由N来决定一条可选飞行路径的最长飞行时间)。在现实世界中,多数的障碍区域是其他飞机。这些距离较远的飞机由于速度太快,对当前的在线优化没有什么用。因此,实际有用的UR的数目并不会随着DD大大增加,这对把RHC用于作洲际飞行有很大的实际意义。
表 5很清楚地表明,应合理地选择N,即滑动地平线的长度。如果N太小,RHC的优化性能就差,如表 5中N=1和N=3的案例。而如果N太大,OCT增加了,但性能并没有进一步提高。相反,在动态案例中,N即太大时RHC的优化性能还可能降低,如表 5中N=9时所示。
表 6显示了RHC中终端加权对优化性能的影响。因为式(19)中定义的Wterm(k)使算法变得不稳定,所以表 6中没有给出相关的结果。基本上,在OCT保持在相同水平时,可以看出在分别使用式(20),式(21),式(22)和式(23)中定义的Wterm(k)后,RHC的性能一步步地得到了改善。原因已在2.3节中详细阐述。
4 结论自由区域路径优化问题与传统的路径优化问题不同。自由区域路径优化问题中不存在路径网络,而是可以在除障碍区之外的整个区域内自由规划路径。障碍区可以是固定于某位置的障碍物,也可以是动态变化的特殊区域,例如台风区域、其他运动体等等。因此,自由区域路径优化问题通常要求针对动态障碍区进行实时路径优化。本研究提出了一种基于遗传算法(GA)和滑动地平线控制(RHC)策略的混和算法来解决此问题。为此目的,首先建立了带动态障碍区的自由区域路径优化问题的数学模型后,然后详细介绍了混和算法的设计思路,全面研究和探讨了此算法的主要技术问题,例如,如何选择RHC的滑动地平线的长度,以及如何使用终端加权。仿真试验结果显示,在缺少不确定因素时,混和算法可以和现存算法达到一样好的性能,而在动态环境中,混和算法的性能(不论求解质量,还是求解速度)则优于现存算法。未来的研究工作可考虑将本文所提出的混合算法应用到更加复杂的实际问题当中,例如:考虑转弯半径的限制,考虑各个时间段可以选用不同的速度,并进一步研究分析滑动地平线长度和终端加权在复杂问题中的效果,等等。
| [1] |
CORMEN T H, LEISERSON C E, RIVEST R L, et al. Introduction to Algorithms[M]. 2nd ed. Cambridge: MIT Press and McGraw-Hill, 2001.
|
| [2] |
韩雪, 刘英舜, 郭唐仪. 城市轨道交通网络中断下的有效路径搜索模型[J]. 公路交通科技, 2015, 32(10): 97-101. HAN Xue, LIU Ying-shun, GUO Tang-yi. A Valid Path Searching Model for Interrupted Urban Rail Transit Network[J]. Journal of Highway and Transportation Research and Development, 2015, 32(10): 97-101. |
| [3] |
WICKENS C D, MAVOR AS, PARASURAMAN R, et al. Airspace System Integration:The Concept of Free Flight[M]. Washington: National Academy Press, 1998.
|
| [4] |
KAHNE S. Research Issues in the Transition to Free Flight[J]. Annual Reviews in Control, 2000, 24(1): 21-29. |
| [5] |
MCLEAN D. Operational Requirements for Fully Automatic Flight[J]. Aircraft Engineering and Aerospace Technology, 2003, 75(6): 570-574. |
| [6] |
胡晓明, 李万莉, 朱为国, 等. 半挂液罐车的避障运动仿真分析[J]. 公路交通科技, 2013, 30(7): 151-158. HU Xiao-ming, LI Wan-li, ZHU Wei-guo, et al. Simulation of Obstacle Avoidance Motion of Liquid Tank Semi-trailer[J]. Journal of Highway and Transportation Research and Development, 2013, 30(7): 151-158. |
| [7] |
GESER A, MUNOZ C. A Geometric Approach to Strategic Conflict Detection and Resolution[C]//AIAA/IEEE Digital Avionics for Commercial and Military Systems-Proceedings. Irvine, US:Institute of Electrical and Electronics Engineers Inc, 2002.
|
| [8] |
PALLOTTINO L, BICCHI A, PANCANTI S. Safety of a Decentralized Scheme for Free-flight ATMS Using Mixed Integer Linear Programming[C]//Proceedings of the American Control Conference. Anchorage, US:Institute of Electrical and Electronics Engineers Inc, 2002:742-747.
|
| [9] |
GRANGER G, DURAND N, ALLIOT J M. Token Allocation Strategy for Free-flight Conflict Solving[C]//Proceedings of Innovative Applications of Artificial Intelligence. Seattle, US:American Association for Artificial Intelligence, 2001:59-64.
|
| [10] |
OH J H. SDP Relaxation Approach to Air Traffic Control Under Free Flight[C]//Proceedings of the 1999 IEEE International Conference on Control Applications. Kohala Coast, US:IEEE, 1999:158-163.
|
| [11] |
SHEWCHUN J M, OH J H, FERON E. Linear Matrix Inequalities for Free Flight Conflict Problems[C]//Proceedings of the 36th IEEE Conference on Decision and Control. San Diego, US:IEEE, 1997:2417-2422.
|
| [12] |
DURAND N, ALLIOT J M, CHANSOU O. Optimal Resolution of En Route Conflicts[J]. Air Traffic Control Quarterly, 2001, 3(3): 253-264. |
| [13] |
WARREN A. Methodology and Initial Results Specifying Requirements for Free Flight Transitions[C]//15th AIAA/IEEE Digital Avionics Systems Conference. Atlanta:IEEE, 1996:87-93.
|
| [14] |
PLAETTNER H, JOACHIM K, ZHAO Y Y J, et al. A Modularized Approach for Comprehensive Air Traffic System Simulation[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Denver:American Institute of Aeronautics and Astronautics Inc, 2000.
|
| [15] |
MCDONALD J A, ZHAO Y. Time Benefits of Free-flight for a Commercial Aircraft[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Devner:American Institute of Aeronautics and Astronautics Inc, 2000.
|
| [16] |
ANDREATTA G, BRUNETTA L, GUASTALLA G. From Ground Holding to Free Flight:An Exact Approach[J]. Transportation Science, 2000, 34(4): 394-401. |
| [17] |
HU X B, WU S F, JIANG J. On-line Free-flight Path Optimization Based on Improved Genetic Algorithms[J]. Engineering Applications of Artificial Intelligence, 2004, 17(8): 897-907. |
| [18] |
CLARKE D. Advances in Model-based Predictive Control[M]. New York: Oxford University Press, 1994.
|
| [19] |
DE SCHUTTER B, VAN DEN BOOM T. Model Predictive Control for Max-plus-linear Discrete Event Systems[J]. Automatica, 2001, 37(7): 1049-1056. |
| [20] |
CHAND S, HSU V N, SETHI S. Forecast, Solution, and Rolling Horizons in Operations Management Problems:A Classified Bibliography[J]. Manufacturing & Service Operations Management, 2002, 4(4): 25-43. |
| [21] |
HU X B, CHEN W H. Receding Horizon Control for Aircraft Arrival Sequencing and Scheduling[J]. IEEE Transaction on Intelligent Transportation System, 2005, 6(2): 189-197. |
| [22] |
胡小兵, 吴树范, 江驹. 民航飞机飞行航线动态实时优化仿真研究[J]. 计算机仿真, 2001, 18(3): 80-83. HU Xiao-bing, WU Shu-fan, JIANG Ju. The Simulation Study On On-line Real-time Optimization of Commercial Aircraft's Flight Paths[J]. Computer Simulation, 2001, 18(3): 80-83. |
 2017, Vol. 34
2017, Vol. 34
