扩展功能
文章信息
- 李立峰, 李辉辉, 徐开铎, 胡思聪
- LI Li-feng, LI Hui-hui, XU Kai-duo, HU Si-cong
- 基于均匀设计响应面法的桥梁地震易损性分析
- Analysis on Bridge Seismic Fragility Based on Uniform Design Response Surface Method
- 公路交通科技, 2017, 34(11): 100-109
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(11): 100-109
- 10.3969/j.issn.1002-0268.2017.11.015
-
文章历史
- 收稿日期: 2016-03-02
2. 湖南大学 风工程与桥梁工程湖南省 重点实验室, 湖南 长沙 410082
2. Key Laboratory for Wind and Bridge Engineering of Hunan Province, Hunan University, Changsha Hunan 410082, China
近年来,地震发生越来越频繁、强度越来越高,导致的危害程度也日趋增大。为了尽量减小地震造成的生命及财产损失,如何将基于性能的抗震设计方法融进目前桥梁抗震设计实践中,是目前桥梁设计方法的重要发展方向。而作为基于性能抗震设计方法及地震风险的评估重要手段,地震易损性分析可以对桥梁结构的抗震性能进行评估与分析,对维护生命线工程的畅通及减少生命财产损失有重要作用。
地震易损性分析,可以反映桥梁结构在不同强度地震动作用下,其地震需求能力超过指定损伤状态的条件概率。易损性曲线将桥梁结构抵抗地震动作用的能力以概率分布的形式表达出来,一般用于衡量桥梁结构在不同强度等级地震动作用下的易损程度。国内外学者对地震易损性分析问题进行了大量的研究。Basoz等[1]基于Loma Prieta和Northridge地震中的桥梁震害统计数据,对美国加州地区的桥梁进行易损性分析,建立了桥梁结构的破坏概率矩阵,采用逻辑回归分析方法得到了桥梁地震易损性曲线。Yamazaki等[2]在日本大阪地震的桥梁震害调查报告的基础上,建立了该地区桥梁的破坏概率矩阵,并分别采用极大似然法和最小二乘法得到了桥梁地震易损性曲线。Banerjee等[3]针对美国加州地区典型的混凝土桥梁,采用反应谱分析方法建立了该地区的桥梁地震易损性曲线。吴文朋等[4]、黄盛楠等[5]基于IDA方法分别对大跨高墩连续刚构桥及斜拉桥进行了易损性分析。H. Hwang等[6]、王其昂等[7]基于蒙特卡罗抽样建立了桥梁地震易损性曲线。李立峰等[8]基于传统可靠度的分析方法,结合拉丁抽样对中等跨径RC梁桥进行了地震易损性分析。张尚荣等[9]在桥梁地震易损性分析方面,采用响应面法拟合结构响应与设计变量的函数,较好地反映了结构损伤与地震动之间的关系。沈国煜等[10]、钟剑等[11]在对斜拉桥进行地震易损性分析时,引入均匀设计建立“结构-地震动”样本,在减少试验样本对数方面取得了较好的效果。以上方法均是建立在极为耗时的非线性有限元计算的基础上,因而计算成本高、效率低,阻碍了其进一步的工程应用。
在地震易损性分析方面,与传统试验设计方法(如全因子设计、正交设计和中心复合设计等)相比,均匀设计方法在建立“结构-地震动”试验样本对时,可以明显减少抽样次数和样本数目,同时又能满足精度要求;响应面法可通过简单显式的响应面函数来近似代替结构响应与结构和地震动参数间复杂的超曲面关系。基于此,综合考虑响应面法及均匀设计在地震易损性分析方面的优点,且鉴于均匀设计响应面法的桥梁地震易损性分析未见文献报道,为研究和推广其运用范围,本研究以一多跨连续梁桥为对象,以桥梁支座位移、墩柱曲率为结构响应,结合均匀设计与二次多项式响应面,建立结构响应与结构和地震动参数之间的响应面模型,得到了桥梁构件和系统的易损性曲线,对桥梁结构抗震性能进行评估。同时,分别使用本研究方法、基于蒙特卡罗、正交设计、中心复合设计的响应面法对算例分析,从抽样次数、有限元计算耗时、响应面模型精度、易损性曲线等方面进行比较,最后得出相应的结论。
1 基于均匀设计响应面法的地震易损性分析方法 1.1 均匀设计均匀设计[12]最早运用于导弹的试验设计,常用于多因子、多水平试验设计。地震易损性分析通常要考虑结构和地震动的不确定性影响,按常规方法分析需要大量试验样本,而通过均匀设计则可以明显减少试验抽样次数,同时保证试验抽样精度,具体可见文献[13-14]。
根据文献[12],以均匀设计表U8(84)为例说明均匀设计的优点。在4因子数8水平数的试验设计中,采用普通全因子试验设计所需样本数为48=65 536;采用正交设计,可将试验样本数减少为82=64;采用中心复合设计时,所需样本数为24+2×4+1=25;而采用均匀设计表U8(84),仅通过8个样本即可充分反映参数的随机性。
1.2 响应面方法响应面方法通过一组试验设计样本点回归拟合,得到响应与设计变量之间复杂的隐式函数关系,是一种试验设计与数理统计相结合的方法[13]。响应面法可通过简单显式的响应面函数来近似代替结构响应与设计变量间的复杂超曲面关系。在实际应用中,可根据工程经验确定多项式响应面模型的形式,通常在设计变量的某个范围内采用低阶多项式,如采用线性函数或二阶多项式来近似拟合[15]。其中,含交叉项的二次多项式响应面函数为:
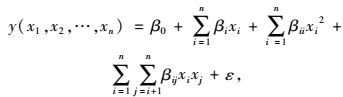
|
(1) |
式中,y为结构响应;n为设计变量的个数;x1, x2, …, xn为设计变量;β(不同下标)为待定系数,共有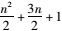
由最小二乘法原理,确定待定系数矩阵β:
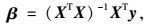
|
(2) |
式中,β为待定系数矩阵,β=[β0, β1, …, βn, β11, …, βnn, β12, …, β(n-1) n]T;X为由参数样本点构成的矩阵,

|
y为结构响应向量,y=[y1, y2, …, yn]T。
由文献[13],评价式(1)所示的响应面对真实极限状态函数的拟合程度,可通过测定拟合系数R2和修正拟合系数Ra2与1的逼近程度来检验(与1越逼近,表示建立的响应面模型与真实极限状态函数曲面的拟合程度越高),其中R2和Ra2的表达式分别为:
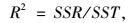
|
(3) |
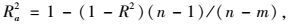
|
(4) |
式中,SSR=βTXTy-(ITy)2/n;SST=yTy-(ITy)2/n; I为单位矩阵。
由均匀设计理论[14],根据设计变量数和均匀设计表偏差,选择合理的均匀设计表来构造试验样本,从而建立结构响应与设计变量间的响应面模型。
1.3 基于均匀设计响应面法的地震易损性分析流程根据均匀设计响应面法的基本原理,本研究提出的基于均匀设计响应面法的地震易损性分析框架如图 1所示。
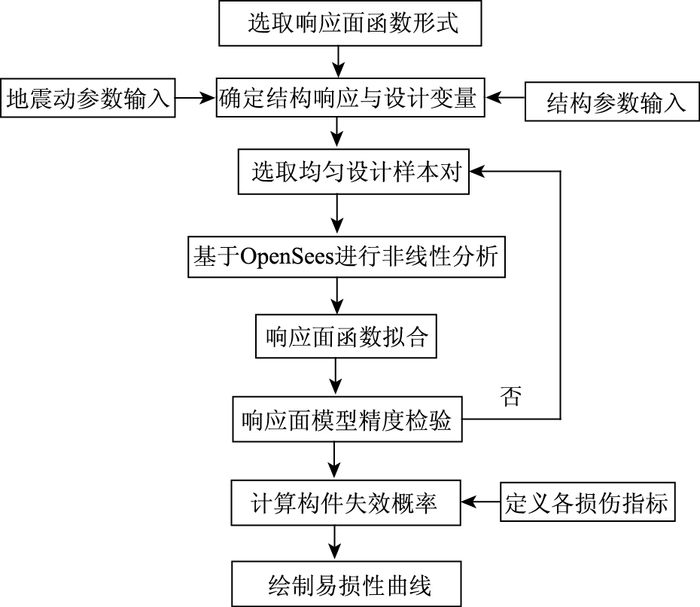
|
| 图 1 均匀设计响应面法的地震易损性分析流程图 Fig. 1 Flowchart of Seismic fragility analysis based on uniform design response surface method |
| |
2 桥梁算例 2.1 桥梁概况与有限元模型
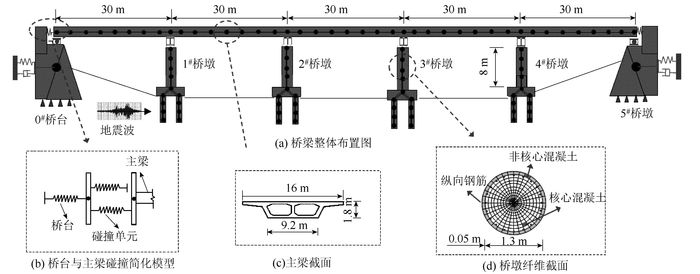
算例桥梁为一座跨径布置为5×30 m的钢筋混凝土多跨连续梁桥,主梁为C50混凝土箱梁,梁高1.8 m;盖梁采用C40混凝土;桥墩为直径1.4 m的钢筋混凝土圆形墩,采用C30混凝土,墩高8 m;纵筋和箍筋均采用HRB335钢筋,纵筋配筋率为1.08%,体积配箍率为0.58%,纵筋直径为28 mm,箍筋直径为10 mm;混凝土保护层厚度为5 cm;支座采用板式橡胶支座;桥台为整体式桥台;桩基采用直径为2.5 m嵌岩桩。
采用OpenSees程序[16]建立桥梁非线性动力有限元模型,如图 2所示。桥梁上部结构采用弹性梁柱单元模拟, 墩柱采用弹塑性纤维单元模拟。在桥墩弹塑性纤维单元中,核心混凝土与非核心混凝土采用Kent-Scott-Park模型,并且不考虑混凝土的抗拉性能;钢筋采用双线性滞回模型。桥台采用Aviram等[17]提出的简化弹簧系统, 采用接触单元法来模拟构件间的碰撞效应。本研究中接触单元模型仅由1个连接弹簧组成,即不考虑碰撞过程中能量的损失,并假定桥台不发生变形。接触单元的非线性力-位移关系为:
|
| 图 2 桥梁有限元模型 Fig. 2 Finite element model of bridge |
| |
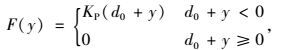
|
(5) |
式中,F(y)为非线性力;d0为桥台与主梁间的初始间隙(即伸缩缝大小);y为地震作用下主梁与桥台的相对位移;KP为接触碰撞刚度,由于缺乏试验依据,在以往的研究中通常假定很大的弹簧刚度,本研究参考主梁的轴向刚度,KP取值为3.02×106 kN/m。
承台底部固结,不考虑桩-土间的相互作用,场地条件为Ⅱ类,地震波仅考虑纵桥向输入。
2.2 结构响应和设计变量的确定为综合考虑结构及地震动的不确定性,本研究根据文献[10],共选取11个设计变量,其中核心混凝土4个参数:峰值强度fc, core,峰值强度时对应的应变εc, core,屈服强度fcu, core,屈服强度时对应的应变εcu, core;非核心混凝土3个参数:峰值强度fc, cover,峰值强度时对应的应变εc, cover,屈服强度时对应的应变εcu, cover;纵向钢筋3个参数:初始刚度E0,屈服强度fy,钢筋硬化比γ;桥墩几何参数:桥墩直径d。结合目前已有研究资料,取桥梁支座位移和墩底截面曲率作为桥梁结构响应,结构随机变量参数如表 1所示。
| 参数名称 | 均值 | 变异系数 | 上限值 | 下限值 |
| fc, core/MPa | 34.47 | 0.20 | 41.364 | 27.576 |
| εc, core | 0.005 | 0.20 | 0.006 | 0.004 |
| fcu, core/MPa | 24.13 | 0.20 | 28.956 | 19.304 |
| εcu, core | 0.02 | 0.20 | 0.024 | 0.016 |
| fc, cover/MPa | 27.58 | 0.20 | 33.096 | 22.064 |
| εc, cover | 0.002 | 0.20 | 0.002 4 | 0.001 6 |
| εcu, cover | 0.006 | 0.20 | 0.007 2 | 0.004 8 |
| fy/MPa | 307.46 | 0.106 | 340.051 | 274.87 |
| E0/MPa | 201 000 | 0.33 | 207 633 | 194 367 |
| γ | 0.02 | 0.20 | 0.024 | 0.016 |
| d/m | 1.4 | 0.05 | 1.455 | 1.345 |
地震动可以通过地面峰值加速度(PGA)、地面峰值速度(PGV)和谱加速度(SA)等强度指标来描述[18]。Mackie等[19]建议,概率分析结果的一致性可以作为地震动强度指标IM能否应用的判定标准,基于此,PGA和PDV均为IM较好的选择。同时,Padgett等[20]对IM进行了效率、可适用性和危害可计算性分析,其研究结果表明,PGA是比较合适的地震动强度指标。因此,本研究选择PGA作为地震动强度指标。根据桥梁场地条件,以《公路桥梁抗震细则》中的设计反应谱为目标反应谱,从美国太平洋地震工程研究中心(PEER)的最新地震动数据库中选取30条地震动记录,地震动加速度反应谱曲线如图 3所示。根据所选择的设计变量和地震动记录,依据均匀设计表U30(3013)最终可获得30个“结构-地震动”试验样本对。
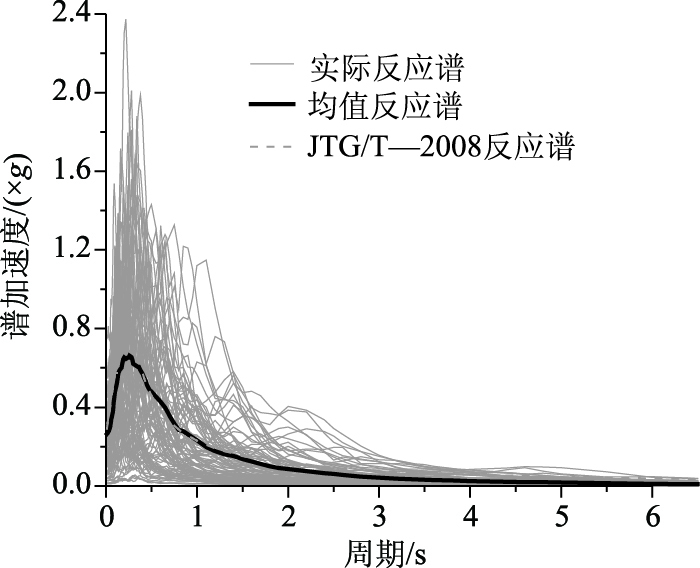
|
| 图 3 地震波反应谱 Fig. 3 Response spectrum of seismic wave |
| |
3 地震需求与易损性分析 3.1 结构概率地震需求模型
根据“结构-地震动”样本对,基于OpenSees进行30次全过程非线性时程分析,记录结构响应峰值,由最小二乘非线性回归分析得到各桥梁构件的概率性地震需求模型,如表 2和图 4所示。算例桥梁为一座规则桥梁,各桥墩支座布置形式相同,因篇幅所限,本研究仅给出1#桥墩,下文不再赘述。由图 4可知,支座位移的能力需求线性拟合较好,而墩柱曲率则采用二次曲线拟合较好。
| 构件需求参数 | 拟合回归方程 | 判定系数R2 | 对数标准差β |
| 支座位移d | ln(d)=0.949 1·ln(PGA)-2.517 5 | 0.972 2 | 0.401 6 |
| 墩柱曲率μ | ln(μ)=0.062 7·ln(PGA)2-6.476 2 | 0.963 5 | 0.455 2 |
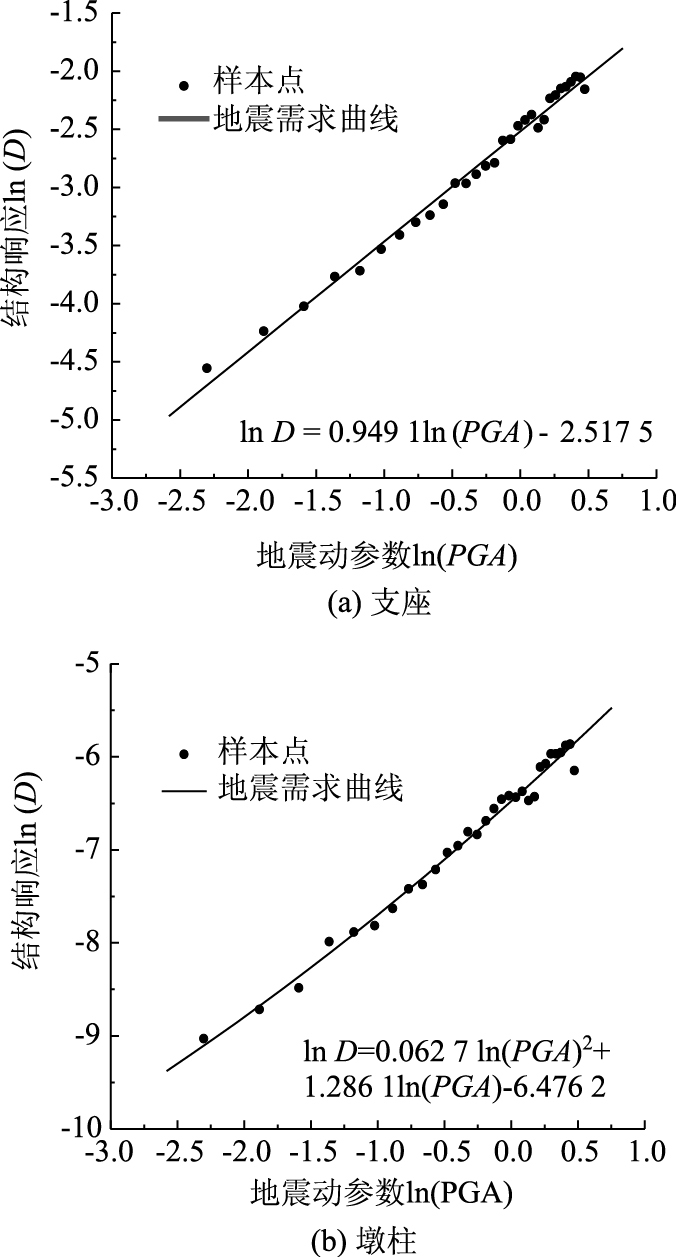
|
| 图 4 桥梁构件概率地震需求模型 Fig. 4 Probabilistic seismic demand models of bridge components |
| |
3.2 易损性分析 3.2.1 损伤指标的确定
选择合理的桥梁结构响应和性能目标在基于性能的桥梁抗震设计中尤为重要。易损性分析中采用的破坏准则可归纳为4类[21]:强度准则、变形准则、能量破坏和变形准则、能量双重准则。本研究采用变形准则,将桥梁损伤状态分为4个等级:(1)轻微损伤;(2)中等损伤;(3)严重损伤;(4)完全破坏。其中,墩柱采用结构曲率延性系数来定义损伤状态,曲率延性系数为墩柱曲率与首次屈服曲率的比值,对各个损伤状态,曲率延性系数的取值[22-23]分别为1.0,2.0,4.0,8.0;而对于支座,则采用容许剪切应变作为损伤指标,对各个损伤状态,分别取值为100%,150%,200%,250%[24],代入式(6)可计算对应的支座位移:
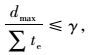
|
(6) |
式中,dmax为支座最大位移;∑te为支座橡胶层厚度。结构损伤指标见表 3。
| 桥梁构件 | 损伤指标 | 损伤状态 | ||||
| 基本完好 | 轻微损伤 | 中等损伤 | 严重损伤 | 完全破坏 | ||
| 墩柱 | 曲率延性系数φ | φ≤1 | 1 < φ≤2 | 2 < φ≤4 | 4 < φ≤8 | φ≥8 |
| 支座 | 容许剪切应变γ | γ≤100% | 100% < γ≤150% | 150% < γ≤200% | 200% < γ≤250% | γ≥250% |
3.2.2 桥梁构件易损性曲线
易损性曲线可以描述为在特定地震强度IM作用下结构需求(D)超出结构能力(C)的条件概率[25],其计算公式为:
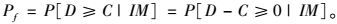
|
(7) |
国内外许多学者在研究过程中,假定结构的能力极限状态服从对数正态分布[22],因此结合地震概率需求模型可以推出,易损性仍然服从对数正态分布。本研究根据文献[25]的方法,利用贝叶斯方法来考虑桥梁结构损伤状态的变异性和不确定性,得到各个桥梁构件在各损伤状态下的结构能力均值和对数标准差,具体如表 4所示,然后可按式(8)计算结构在不同水平地震下的失效概率,从而绘制桥梁构件易损性曲线(图 5)。
| 桥梁构件需求参数 | 轻微损伤 | 中等损伤 | 严重损伤 | 完全破坏 | ||||
| SC | βC | SC | βC | SC | βC | SC | βC | |
| 支座位移d/mm | 6.456 | 0.246 | 20.581 | 0.246 | 42.162 | 0.472 | 182.790 | 0.633 |
| 墩柱曲率延性系数φ | 1.293 | 0.418 | 2.218 | 0.427 | 4.736 | 0.634 | 6.247 | 0.635 |
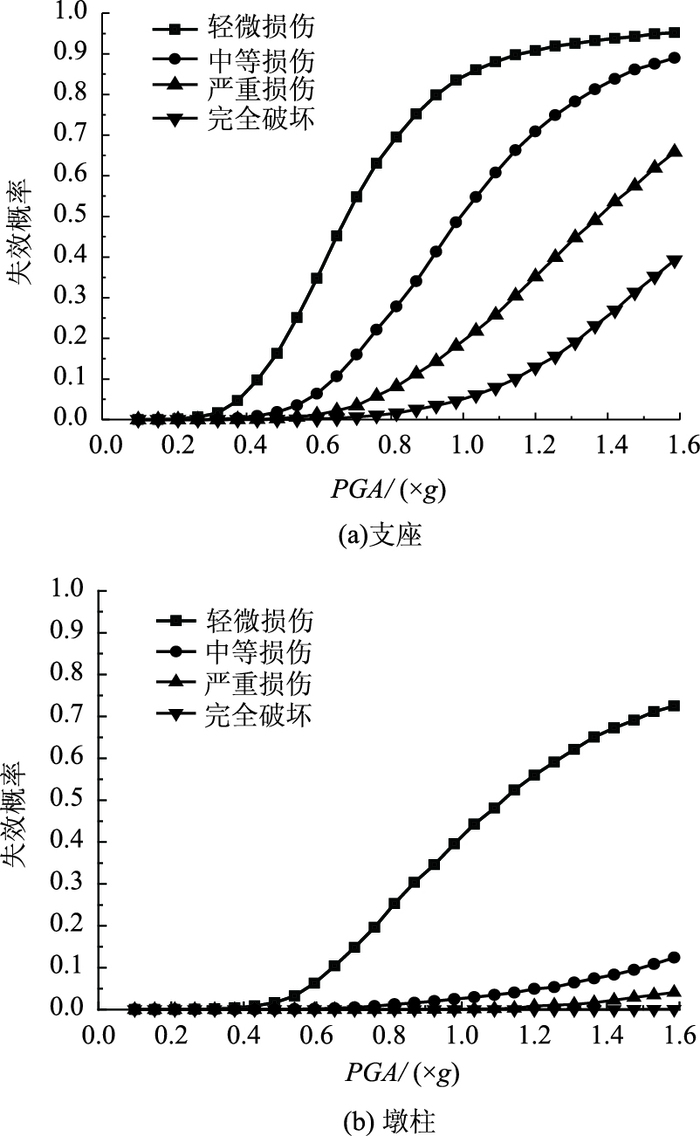
|
| 图 5 构件易损性曲线 Fig. 5 Fragility curves of components |
| |
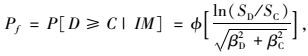
|
(8) |
式中,SD和SC分别为结构需求和能力均值;βD和βC分别表示为结构需求和能力对数标准差。
由图 5可知,桥梁支座在轻微损伤与中等损伤、严重损伤和完全破坏下失效概率为50%时对应的PGA分别超过了0.6g和1.2g,表明桥梁结构具有足够的抗震能力,墩柱发生严重损伤和完全破坏的失效概率很小,满足抗震设计规范的要求。
3.2.3 桥梁系统易损性曲线桥梁是由不同的结构构件组成的复杂组合体系,仅仅依靠构件层次的易损性曲线不足以全面评估其整体抗震性能,因此,对桥梁系统层次的易损性分析显得尤为重要。本研究采用一阶界限法[26]来进行桥梁系统易损性分析。一阶界限法也称为宽界限法,可对全桥结构系统进行保守估计,由式(9)可计算得到桥梁系统层次易损性曲线,见图 6。
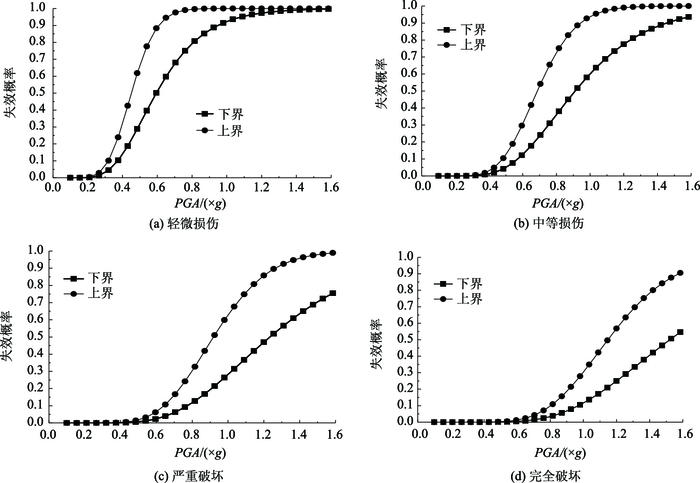
|
| 图 6 桥梁系统易损性曲线 Fig. 6 Fragility curves of bridge system |
| |
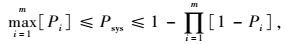
|
(9) |
式中,m为构件数;Pi为第i个构件的失效概率;Psys为桥梁系统失效概率。
由图 6可以看出,轻微损伤、中等损伤、严重损伤和完全破坏下,与桥梁系统损伤超越概率50%时对应的PGA上下界限分别为0.43g和0.62g、0.65g和0.85g、0.83g和1.15g、1.15g和1.57g。与桥梁构件层次的易损性曲线相比,桥梁系统比构件更易破坏。同时,一阶界限法计算的上下界限带宽较大,并且随PGA的增大而变大,这种趋势则会越来越明显。
4 基于响应面法的易损性分析比较 4.1 四种方法的抽样次数和计算耗时比较为进一步检验本研究方法的有效性,在上述有限元模型的基础上,分别用本研究方法、基于蒙特卡罗、正交设计和中心复合设计的响应面法对其分析。为保证试验抽样精度,进行了10 000次蒙特卡罗抽样。由于蒙特卡罗方法抽样次数多、精度高,常用来验证其他方法的有效性的特点。本研究以MCS方法为基准,分别对本研究方法、ODS和CDS方法在抽样次数和有限元分析计算耗时方面进行了比较(图 5)。由表 5可以看出:(1)抽样次数方面,与MCS方法相比,CDS方法与ODS方法的抽样次数分别为4 121次和900次,而本研究方法仅为30次,比MCS方法、CDS方法、ODS方法分别减少了99.70%,58.49%,8.70%;(2)有限元分析计算耗时方面,MCS方法所需时间为1 500 000 s,而CDS方法、ODS方法和本研究方法分别耗时为618 150,135 000,4 500 s,本研究方法分别比MCS方法、CDS方法和ODS方法减少了99.70%,58.49%,8.70%。因此,本研究方法在抽样次数和有限元计算耗时方面有较好的性能。
| 比较项目 | 抽样次数/次 | 计算耗时/s | 抽样次数相对值/% | 计算耗时相对值/% |
| MCS | 10 000 | 1 500 000 | 100.00 | 100.00 |
| ODS | 900 | 135 000 | 9.00 | 9.00 |
| CDS | 4 121 | 618 150 | 41.21 | 41.21 |
| 本研究方法 | 30 | 4 500 | 0.30 | 0.30 |
| 注:MCS方法为基于蒙特卡罗的响应面法;ODS方法为基于正交设计的响应面法;CDS方法为基于中心复合设计的响应面法(下同);抽样次数相对值为其他方法抽样次数与MCS方法抽样次数的比;计算耗时相对值为其他方法计算耗时与MCS方法计算耗时的比。 | ||||
4.2 四种方法的结构响应面精度比较
为比较4种方法所建立的结构响应面模型精度,有必要对各方法所建立的响应面模型的拟合系数R2和修正拟合系数Ra2进行比较,桥梁支座位移和墩柱曲率响应面模型精度比较结果见表 6和表 7。
| 方法 | 比较项目 | 桥梁支座位移响应面拟合系数 | |||
| 均值响应面拟合系数 | 标准差响应面拟合系数 | 均值响应面拟合系数相对值/% | 标准差响应面拟合系数相对值/% | ||
| MCS | R2 | 0.980 8 | 0.986 2 | 100 | 100 |
| Ra2 | 0.987 6 | 0.984 5 | 100 | 100 | |
| ODS | R2 | 0.872 4 | 0.865 7 | 88.95 | 87.78 |
| Ra2 | 0.856 3 | 0.839 6 | 87.50 | 85.28 | |
| CDS | R2 | 0.908 3 | 0.912 3 | 92.61 | 92.51 |
| Ra2 | 0.908 6 | 0.901 8 | 92.85 | 91.60 | |
| 本研究方法 | R2 | 0.946 4 | 0.951 4 | 96.49 | 96.47 |
| Ra2 | 0.933 5 | 0.929 1 | 95.39 | 94.37 | |
| 方法 | 比较项目 | 桥梁墩柱曲率响应面拟合系数 | |||
| 均值响应面拟合系数 | 标准差响应面拟合系数 | 均值响应面拟合系数相对值/% | 标准差响应面拟合系数相对值/% | ||
| MCS | R2 | 0.986 8 | 0.981 7 | 100.00 | 100.00 |
| Ra2 | 0.972 5 | 0.979 4 | 100.00 | 100.00 | |
| ODS | R2 | 0.832 5 | 0.823 5 | 84.36 | 83.89 |
| Ra2 | 0.815 9 | 0.807 1 | 83.90 | 82.40 | |
| CDS | R2 | 0.917 4 | 0.905 5 | 92.97 | 92.24 |
| Ra2 | 0.905 8 | 0.912 5 | 93.14 | 92.95 | |
| 本研究方法 | R2 | 0.947 9 | 0.949 7 | 96.06 | 96.74 |
| Ra2 | 0.936 5 | 0.930 2 | 96.30 | 94.98 | |
| 注:MCS,ODS,CDS,R2,Ra2的意义同上。均值和标准差响应面拟合系数相对值分别为其他方法与MCS方法的响应面拟合系数之比。 | |||||
由表 6可知,在桥梁支座位移响应均值和标准差响应面拟合系数方面,与MCS方法相比,ODS方法与CDS方法分别减小了11%~15%和7%~9%,而本研究方法则减少了3%~5%。由表 7可看出,在桥梁墩柱曲率响应均值和标准差响应面拟合系数方面,ODS方法和CDS方法分别减小了15%~18%和6%~8%,而本研究方法则减少了3%~5%。因此,本研究方法所建立的结构响应面模型精度与MCS方法较接近,表明本研究方法能够较好地拟合结构真实的极限状态函数曲面,并且能够较好地反映结构响应的基本特征。
4.3 四种方法的易损性曲线比较为进一步检验本研究方法在桥梁地震易损性分析方面的效果,有必要对4种方法各损伤状态下的易损性曲线进行比较。由以上分析知,支座相比于墩柱更易破坏,此处仅比较支座易损性曲线,如图 7所示。
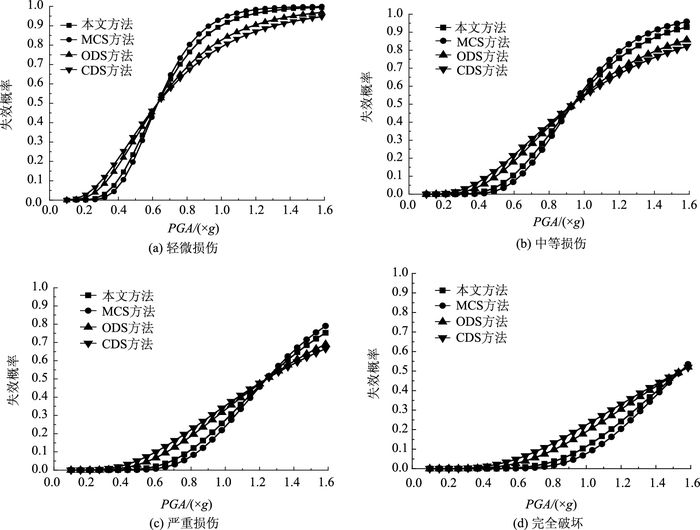
|
| 图 7 四种方法支座易损性曲线比较 Fig. 7 Comparison of component fragility curves among 4 methods |
| |
由图 7可知,4种方法所得易损性曲线整体趋势相同,但与MCS方法相比,其他3种方法均有一定的偏差。在MCS方法中,采用了蒙特卡罗抽样,其抽样次数足够多,故基于MCS方法的桥梁地震易损性分析最为精确,得到的易损性曲线也能对桥梁构件在各损伤状态下的失效概率进行准确评估,常用来验证其他方法的有效性和可靠性。由图 7可知,其他3种方法得到的易损性曲线均在MCS方法的包络范围内,符合以往研究的结论。然而,MCS方法的精确和优越性是基于大量非线性有限元分析的结果,这势必会影响其在桥梁地震易损性分析时效性方面的功能。因此,由图 7可知,本研究方法与MCS方法偏差相对较小,相对误差为3%左右,表明本研究方法能明显减少抽样次数和有限元计算耗,同时能满足精度要求,可以有效地适用于桥梁地震易损性分析。
5 结论(1) 本研究提出的均匀设计响应面法,其易损性分析结果与基于蒙特卡罗的响应面法的相对偏差约为3%,在桥梁地震易损性分析中有良好的有效性和适用性。
(2) 本研究方法在抽样次数、有限元计算耗时方面与基于蒙特卡罗、中心复合设计和正交设计的响应面法相比,分别减少了99.70%,58.49%,8.70%,在抽样次数和有限元计算耗时方面有较好的性能。
(3) 本研究方法建立的结构响应面模型与基于中心复合设计和正交设计的响应面法相比,其精度分别提高了8%~12%和3%~5%,能更好地对结构的真实复杂极限状态函数曲面进行拟合,可以较好地反映结构基本特征。
| [1] |
BASOZ N, KIREMIDJIAN A S. Evaluation of Bridge Damage Data from the Loma Prieta and Northridge, California Earthquakes, No.127[R]. Stanford:Blume Earthquake Engineering Center, 1997.
|
| [2] |
YAMAZAKI F, MOTOMURA H, HAMADA T. Damage Assessment of Expressway Networks in Japan Based on Seismic Monitoring[C]//Proceedings of the 12th World Conference on Earthquake Engineering. Auckland:John Wiley & Sons, 2000:1-8.
|
| [3] |
BANERJEE S, SHINOZUKA M. Nonlinear Static Procedure for Seismic Vulnerability Assessment of Bridges[J]. Computer-Aided Civil and Infrastructure Engineering, 2007, 22(4): 293-305. |
| [4] |
吴文朋, 李立峰, 王连华, 等. 基于IDA的高墩大跨桥梁地震易损性分析[J]. 地震工程与工程振动, 2012, 32(3): 117-123. WU Wen-peng, LI Li-feng, WANG Lian-hua, et al. Evaluation of Seismic Vulnerability of High-pier Long-span Bridge Using Incremental Dynamic Analysis[J]. Journal of Earthquake Engineering and Engineering Vibration, 2012, 32(3): 117-123. |
| [5] |
黄盛楠, 杨德圣, 宋波, 等. 大跨斜拉桥地震易损性分析[J]. 工程力学, 2014, 31(增1): 86-90. HUANG Sheng-nan, YANG De-sheng, SONG Bo, et al. Seismic Vulnerability Analysis for Long-span Cable-stayed Bridge[J]. Engineering Mechanics, 2014, 31(S1): 86-90. |
| [6] |
HWANGH, 刘晶波. 地震作用下钢筋混凝土桥梁结构易损性分析[J]. 土木工程学报, 2004, 37(6): 47-51. HWANG H, LIU Jing-bo. Seismic Fragility Analysis of Reinforced Concrete Bridges[J]. Journal of China Civil Engineering, 2004, 37(6): 47-51. |
| [7] |
王其昂, 吴子燕, 贾兆平, 等. 桥梁系统地震多维易损性分析[J]. 工程力学, 2013, 30(10): 192-197. WANG Qi-ang, WU Zi-yan, JIA Zhao-ping, et al. Multi-dimensional Fragility Analysis of Bridge System under Earthquake[J]. Engineering Mechanics, 2013, 30(10): 192-197. |
| [8] |
李立峰, 吴文朋, 黄佳梅, 等. 地震作用下中等跨径RC连续梁桥系统易损性研究[J]. 土木工程学报, 2012, 32(3): 152-160. LI Li-feng, WU Wen-peng, HUANG Jia-mei, et al. Study on System Vulnerability of Medium Span Reinforced Concrete Continuous Girder Bridge under Earthquake Excitation[J]. China Civil Engineering Journal, 2012, 32(3): 152-160. |
| [9] |
张尚荣, 谭平, 杜永峰, 等. 基于响应面法的层间隔震结构地震易损性分析[J]. 振动与冲击, 2014, 33(15): 42-48. ZHANG Shang-rong, TAN Ping, DU Yong-feng, et al. Seismic Fragility Analysis of Inter-story Isolation Structures Based on Response Surface Method[J]. Journal of Vibration and Shock, 2014, 33(15): 42-48. |
| [10] |
BARBATO M, GU Q, CONTE J P. Probabilistic Push-over Analysis of Structural and Soil-structure Systems[J]. Journal of Structural Engineering, 2010, 136(11): 1330-1341. |
| [11] |
钟剑, 庞于涛, 曹飒飒, 等. 基于构件的RC连续梁桥地震体系易损性分析[J]. 同济大学学报:自然科学版, 2015, 43(2): 193-198. ZHONG Jian, PANG Yu-tao, CAO Sa-sa, et al. Seismic Fragility Methodology for RC Continuous Bridges Based on Components Correlation[J]. Journal of Tongji University:Natural Science Edition, 2015, 43(2): 193-198. |
| [12] |
方开泰. 均匀设计与均匀设计表[M]. 北京: 科学出版社, 1994. FANG Kai-tai. Uniform Design and Uniform Design Table[M]. Beijing: Science Press, 1994. |
| [13] |
胡常福, 李辉辉, 任伟新, 等. 基于响应面的新型索拱桥非线性索力优化[J]. 中南大学学报:自然科学版, 2015, 46(11): 4267-4273. HU Chang-fu, LI Hui-hui, REN Wei-xin, et al. Nonlinear Cable Force Optimization of New Type Arch Bridges with Diagonal Web Cables Based on Response Surface Method[J]. Journal of Central South University:Natural Science Edition, 2015, 46(11): 4267-4273. |
| [14] |
吕大刚, 贾明明, 李刚. 结构可靠度分析的均匀设计响应面法[J]. 工程力学, 2011, 28(7): 109-116. LÜ Da-gang, JIA Ming-ming, LI Gang. Uniform Design Response Surface Method for Structural Reliability Analysis[J]. Engineering Mechanics, 2011, 28(7): 109-116. |
| [15] |
李莉, 张赛, 何强, 等. 响应面法在试验设计与优化中的应用[J]. 实验研究与探索, 2015, 34(8): 41-45. LI Li, ZHANG Sai, HE Qiang, et al. Application of Response Surface Methodology in Experiment Design and Optimization[J]. Research and Exploration in Laboratory, 2015, 34(8): 41-45. |
| [16] |
MAZZONI S, MCKENNA F, SCOTT M H, et al. OpenSees Command Language Manual[M]. Berkeley: Pacific Earthquake Engineering Research(PEER) Centre, 2006.
|
| [17] |
AVIRAM A, MACKIE K, STOJADINOVI Ć B. Guidelines for Nonlinear Analysis of Bridge Structures in California[R]. Berkeley:University of California, 2008.
|
| [18] |
MACKIE K R, STOJADINOVI B. Performance-based Seismic Bridge Design for Damage and Loss Limit States[J]. Earthquake Engineering & Structural Dynamics, 2007, 36(13): 1953-1971. |
| [19] |
MACKIE K R, STOJADINOVI B. Fragility Basis for California Highway Overpass Bridge Seismic Decision Making[M]. Berkeley: University of California, 2005.
|
| [20] |
PADGETT J E, NIELSON B G, DESROCHES R. Selection of Optimal Intensity Measures in Probabilistic Seismic Demand Models of Highway Bridge Portfolios[J]. Earthquake Engineering & Structural Dynamics, 2008, 37(5): 711-725. |
| [21] |
CHOI E, DESROCHES R, NIELSON B. Seismic Fragility Curves of Typical Bridges in Moderate Seismic Zones[J]. Engineering Structures, 2004, 26(2): 187-199. |
| [22] |
YANG C S, DESROCHES R, PADGETT J E. Fragility Curves for a Typical California Box Girder Bridge[C]//Proceedings of TCLEE 2009 ASCE Technical Council on Lifeline Earthquake Engineering Conference. Reston:ASCE, 2009:1-12.
|
| [23] |
李立峰, 吴文朋, 黄佳梅, 等. 板式橡胶支座地震易损性分析[J]. 湖南大学学报:自然科学版, 2011, 38(11): 1-6. LI Li-feng, WU Wen-peng, HUANG Jia-mei, et al. Research on the Seismic Vulnerability Analysis of Laminated Rubber Bearing[J]. Journal of Hunan University:Natural Science Edition, 2011, 38(11): 1-6. |
| [24] |
PADGETT J E, DESROCHES R. Methodology for the Development of Analytical Fragility Curves for Retrofitted Bridges[J]. Earthquake Engineering and Structural Dynamics, 2008, 37(8): 1157-1174. |
| [25] |
NIELSON B G, DESROCHES R. Seismic Fragility Methodology for Highway Bridge Using a Component Level Approach[J]. Earthguake Engineering & Structural Dynamics, 2007, 36(6): 823-839. |
| [26] |
CORNELL C A. Bounds on the Reliability of Structure System[J]. Journal of Structure Division, 1967, 93(1): 171-200. |
 2017, Vol. 34
2017, Vol. 34
