扩展功能
文章信息
- 谢峻, 潘宝林, 周毅姝
- XIE Jun, PAN Bao-lin, ZHOU Yi-shu
- 截面收缩徐变非一致性分布与T梁桥腹板竖向开裂的时变相关性
- Time-dependent Correlation between Non-uniformity Distribution of Cross-section Shrinkage and Creep and Vertical Cracking in Web of T-shaped Beam Bridge
- 公路交通科技, 2017, 34(11): 79-83, 109
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(11): 79-83, 109
- 10.3969/j.issn.1002-0268.2017.11.012
-
文章历史
- 收稿日期: 2017-03-18
混凝土的收缩、徐变的研究自20世纪30年代开始至今已经接近百年,积累了大量研究成果,创建了一批较为可靠的理论模型,对其总体规律进行表征。这其中CBE-FIP的MC78和MC90[1]模型分别为我国1985版[2]和2004版[3]的桥梁设计规范所采用,用于桥梁收缩、徐变效应的计算分析。这种应用模式的一个重要假设认为在混凝土结构断面的每一个部位的收缩、徐变均按同样的规律变化(虽然徐变受应力影响其不同位置的绝对应变不同,但其变化规律仍然相同),称为收缩、徐变的一致性假设。理论上这种一致性假设应该限制于一定的范围,而实际上目前在不同类型和跨径的桥梁结构上不加区别地使用。许航等人结合实际工程对截面非均匀性进行了验证性计算研究[4],湖南大学方志等人结合实桥测量的数据、室内模型试验也对截面收缩、徐变非一致性分布效应的影响进行了研究[5]。本文作者也曾对某箱梁桥的同一截面的顶底板收缩、徐变进行了实桥测试,结果表明有明显差异[6]。Z. P. Baíant[7-8],Vladimír Krístek[9],Robert Benaim[10]等人的研究表明桥梁截面顶底板存在不一致的收缩差异是导致混凝土桥梁运营若干年后跨中出现超出预期的下挠的重要原因。项贻强[11]的数值计算结果表明混凝土收缩、徐变非均匀性对结构应力有重要影响。因此,收缩、徐变在截面非一致分布是一种实际存在的结构现象,与单纯材料层次的收缩、徐变研究不同,其形成机理较为复杂,具有结构、材料与环境相互耦合的特征,目前对其研究还仍然不够不充分[12-13]。
T梁腹板的竖向裂缝是一种较为常见的T梁病害,对结构的承载力,特别是抗剪能力有较大的削弱[14-15]。虽然有研究试图从施工原因上分析[16],但更多的实际观测表明,这种腹板裂缝,呈现两头尖中间宽的形态,通常贯通腹板厚度,有些情况下在架设时尚未出现,而是1~2 a后才逐渐出现,显然和时间相关的因素有密切的关系。影响截面收缩、徐变的主要因素除材料层面的外,主要为结构配筋,截面尺寸及环境温度、湿度的变化[12, 17],T梁桥沿高度的截面厚度与配筋变化极为剧烈,收缩、徐变在截面非一致分布的影响较为明显,由于T梁梁高和大跨径混凝土梁比仍然较小,环境因素并不突出,主要为配筋及截面形式的变化,本文因此推导了T梁截面的收缩、徐变非一致性分布计算方法,从此角度对形成具有时间依存性的T梁腹板竖向裂缝的开裂原因进行了理论上的推导和计算验证,为在设计中考虑此因素提供了理论手段。
1 混凝土T梁截面收缩、徐变非一致性效应的计算方法 1.1 钢筋对收缩、徐变的影响对于t0时刻加载的无钢筋的轴压混凝土截面,则t时刻的收缩、徐变应变增量为:
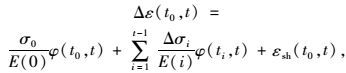
|
(1) |
式中φ为徐变系数;εsh为收缩应变;Δσ(i)为ti-1到ti时刻的应力增量。显然钢筋的存在,将阻碍混凝土的变形,设钢筋和混凝土的应变增量分别为Δεs和Δεc,根据截面轴力等量转换的原则,从截面混凝土部分卸载的轴力由截面钢筋承担,则有:
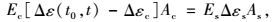
|
(2) |
考虑钢筋和混凝土变形协调,Δεs=Δεc,并设钢筋与混凝土弹模比n=Es/Ec,钢筋配筋率ρ=As/(As+Ac),其中Ac为扣除钢筋的混凝土净面积,则混凝土的实际应变增量为:
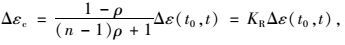
|
(3) |
式中KR即为考虑配筋的影响系数,则由于钢筋的阻碍作用在混凝土中产生的应力增量为:
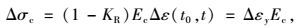
|
(4) |
将T梁截面沿梁高进行切分,如图 1(b)所示,考虑各层间收缩、徐变的无约束自由伸缩,则沿梁高的自由变形,如图 1(c)所示,显然由于每层配筋率、理论厚度和恒载应力的差异,每层的应变值的变化是不同步的。T梁桥的跨高比远大于2.5,其截面应变分布符合平截面假定[18]。由于每层间实际是相互约束的,按平截面假定,截面应变强迫为直线分布,如图 1(d)所示,自由变形与约束变形的差,产生截面的自平衡应力。取截面每层厚度中点的应变代表整层的应变,混凝土截面由于收缩、徐变产生的自应力为:
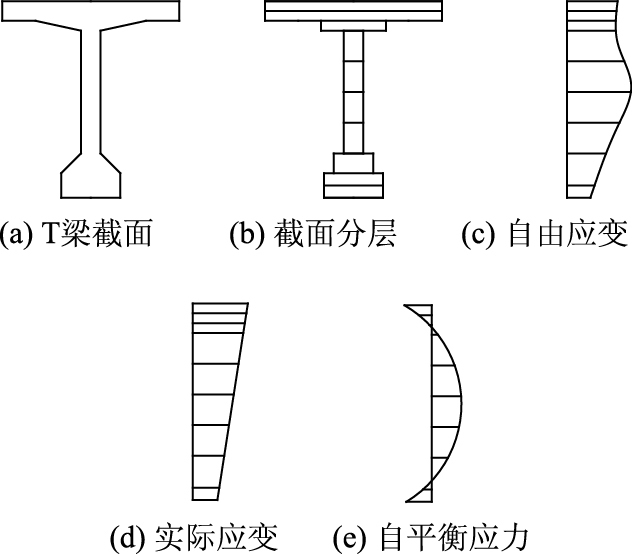
|
| 图 1 T梁收缩、徐变的自平衡应力 Fig. 1 Self balanced stress of shrinkage and creep in T-shaped beam |
| |
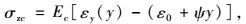
|
(5) |
式中εy(y)为沿截面梁高各层收缩、徐变产生的自由应变;ε0为平截面假定下的梁底应变;ψ为截面曲率。由截面自平衡轴力N和弯矩M为零的条件有:
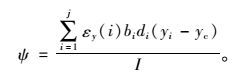
|
(6) |
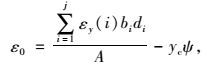
|
(7) |
式中,j为截面分层数;bi为每层的宽度;di为每层的宽度;yc为截面形心距梁底的距离;yi为每层厚度中心距梁底的距离;I为分层截面总惯性矩;A为分层截面总面积。
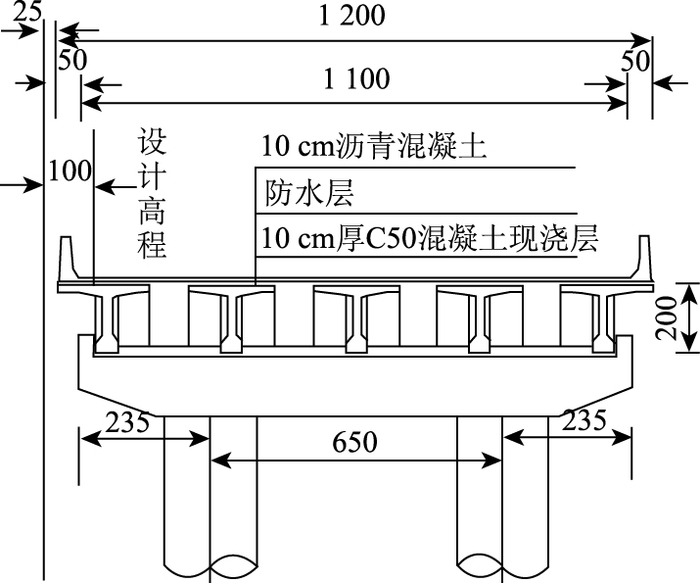
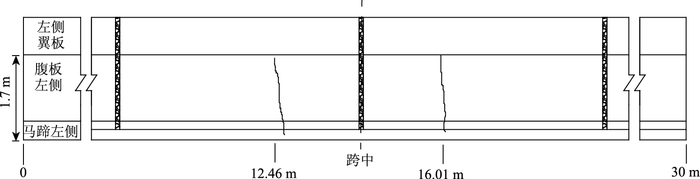
2 实桥验证研究某3跨简支转结构连续A类构件预应力混凝土T梁桥,混凝土标号C50,跨径组合为3×30 m,桥宽12 m,截面由5片2 m高的T梁构成,如图 2所示,在架桥时,T梁未见裂缝,1 a左右的全桥交工验收也未发现裂缝,在完成3 a后的检测时却发现T梁腹板不同程度出现了腹板竖向裂缝,这些腹板裂缝的特点是裂缝中间宽,两头窄,贯穿板厚,在腹板高度范围内分布。典型的如图 3和图 4所示。
|
| 图 2 桥梁断面(单位:cm) Fig. 2 Cross-section of bridge(unit:cm) |
| |
|
| 图 3 T梁腹板的裂缝分布 Fig. 3 Crack distribution of T-shaped beam web |
| |

|
| 图 4 实际腹板竖向裂缝照片 Fig. 4 Photo for vertical crack in web of T-shaped beam |
| |
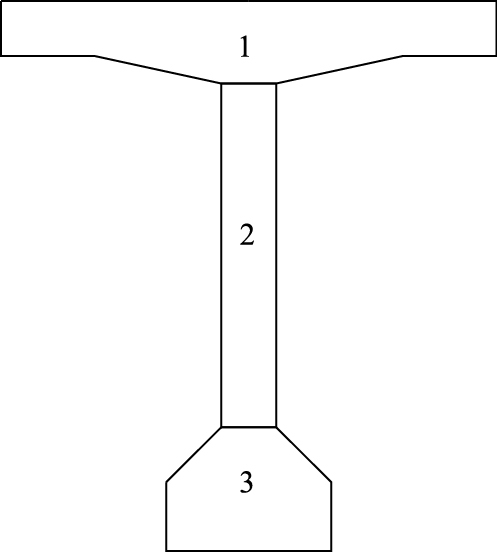
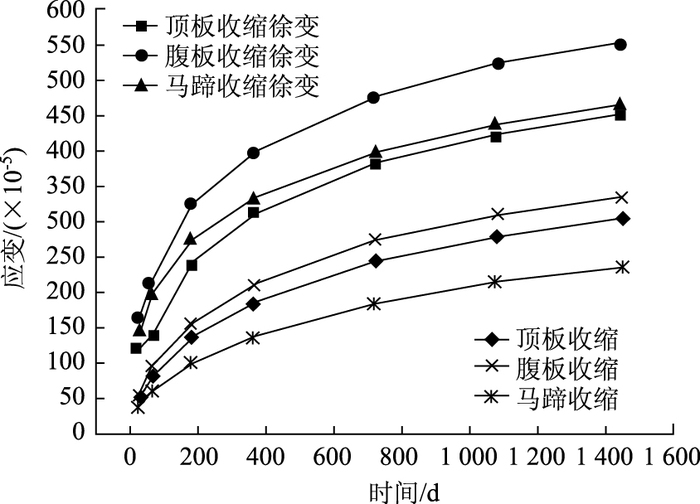
出于说明问题的角度将该桥T梁断面划分为3层,如图 5所示,精细的计算可以多划分几层。跨中断面3部分的纵筋配筋率分别为0.92%,0.28%和3.23%,理论厚度分别为:22.3,20 cm和27.6 cm。采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004) [3]收缩、徐变模式,考虑钢筋的影响,3部分独立的收缩、徐变应变值合计值与单独的收缩应变值,如图 6所示,其中徐变的应变值按中跨跨中截面的恒载应力状态分段计算。
|
| 图 5 收缩徐变非一致性分析模型 Fig. 5 Analysis model of NUDSC |
| |
|
| 图 6 考虑钢筋影响T梁跨中截面各部位独立收缩、徐变应变 Fig. 6 Shrinkage and creep strain of each independent part at mid-span section of T-shaped beam considering influence of rebar |
| |
图 6表明受到体表比和钢筋配筋率的影响,T梁截面的收缩应变是不同步发展的,如果不受约束,最大的腹板收缩应变是最小的马蹄收缩应变的1.6~1.4倍,且随时间增长倍数逐渐缩小,相对马蹄,则顶板和腹板的差距比较小。考虑徐变后,由于截面应力的影响,其规律有所变化,顶板和马蹄的应变变得接近,最大的腹板的收缩、徐变应变是最小的顶板的1.4~1.2倍,随时间增长倍数逐渐缩小。结合图 6,由式(5) ~式(7)计算T梁截面各部分应力如表 1所示。
| 时间/d | 30 | 60 | 180 | 360 | 720 | 1 080 | 1 445 |
| 顶板/MPa | -0.52 | -0.96 | -0.88 | -0.92 | -0.95 | -0.97 | -0.97 |
| 腹板/MPa | 0.79 | 1.07 | 1.59 | 1.89 | 2.14 | 2.27 | 2.28 |
| 马蹄/MPa | 0.01 | 0.42 | -0.20 | -0.46 | -0.65 | -0.76 | -0.78 |
| 注:表中应力以拉为正,压为负。 | |||||||
表 1表明,腹板自应力处于受拉状态,随着成梁时间的延长,腹板自应力(拉应力)不断增大,由浇注后30 d的0.79 MPa,其间经历体系转换、成桥铺装等施工过程,到第3年时已高达2.27 MPa,并基本稳定,进入缓慢增长的阶段,在腹板受拉的同时,顶板和马蹄受压。
收缩、徐变的截面自应力分布的特点是上下缘受压,腹板受拉和原有中跨跨中正应力叠加后,梁体上下缘增大了压应力,但对于组合荷载下的腹板,由于本身压应力就较小,仅有1.3 MPa,增加腹板自应力后,腹板转而受拉,在第1年为0.6 MPa,到第3年已达1.2 MPa。虽然单一的自应力不足以导致腹板开裂,但一般设计并不考虑此项随时间变化的应力,已大大增加了开裂风险,是导致预应力T梁开裂的重要原因。实际上调查表明该梁梁端的抗震拉杆和中间墩抗震锚栓由于施工安装时已拧紧和抵死,导致梁体伸缩受到约束,此因素引起的中跨跨中腹板应力增量为1.65 MPa,和表 2应力叠加,第1年腹板应力2.26 MPa,第2年腹板应力2.64 MPa,第3年腹板应力2.86 MPa,即在T梁浇注后1年(已成桥),腹板的拉应力水平尚没有突破C50混凝土的抗拉应力标准值2.65 MPa,到第2年已基本接近,第3年时则已突破限值,计算结果与实际裂缝出现的时间情况基本吻合。
| 项次 | 应力组合 | 中跨跨中/MPa | ||
| 上缘 | 腹板 | 下缘 | ||
| Ⅰ | ①原结构组合应力1 a | -0.61 | -1.28 | -1.17 |
| ②截面收缩徐变自应力1 a | -0.92 | 1.89 | -0.46 | |
| ①+② | -1.53 | 0.61 | -1.63 | |
| Ⅱ | ①原结构组合应力2 a+ | -0.64 | -1.15 | -0.99 |
| ②截面收缩徐变自应力2 a | -0.95 | 2.14 | -0.65 | |
| ①+② | -1.59 | 0.99 | -1.64 | |
| Ⅲ | ①原结构组合应力3 a | -0.68 | -1.06 | -0.85 |
| ②截面收缩徐变自应力3 a | -0.97 | 2.27 | -0.76 | |
| ①+② | -1.65 | 1.21 | -1.61 | |
| 注:原结构组合应力为荷载短期组合下的应力组合包络值,考虑的因素包括自重+收缩徐变+预应力+基础沉降+汽车荷载+年温差+温度梯度。 | ||||
3 结论
综上所述,本文的主要结论如下:
(1) T梁随着跨径的增长,梁高变高,梁体纤薄,其顶板、腹板和马蹄的配筋和理论厚度存在较大差异,收缩、徐变在截面上容易形成不同步或差异较大的非一致性分布情况。
(2) 收缩、徐变非一致性分布的效应是腹板竖向裂缝产生的重要原因。
(3) 本文考虑T梁实际的截面配筋与理论厚度情况,推导并提出了T梁截面收缩、徐变非一致分布效应的计算方法,实桥计算验证了计算方法的有效性,为考虑此效应提供了理论方法。
| [1] |
Euro-International Committee for Concrete. CEB-FIP Model Code 1990:Design Code[M]. London: Thomas Telford Ltd., 1993.
|
| [2] |
JTJ 023-85, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTJ 023-85, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [3] |
JTG D62-2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62-2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [4] |
许航, 谭景文, 李隆. 截面非均匀收缩对大跨径混凝土箱形梁桥长期变形的影响[J]. 公路, 2010(4): 99-102. XU Hang, TAN Jin-wen, LI Long. Influence of Cross-section Non-uniform Shrinkage on Long-term Deformation of Long-span Concrete Box Girder Bridge[J]. Highway, 2010(4): 99-102. |
| [5] |
汪剑, 方志. 大跨预应力混凝土箱梁桥收缩徐变效应测试与分析[J]. 土木工程学报, 2008, 41(1): 70-81. WANG Jian, FANG Zhi. Analysis and Field Measurement of Concrete Box Girder Bridges for Shrinkage and Creep Effects[J]. China Civil Engineering Journal, 2008, 41(1): 70-81. |
| [6] |
谢峻, 曾丁, 郑晓华. 基于收缩徐变自辨识的大跨径梁桥长期挠度预测[J]. 公路交通科技, 2013, 30(8): 88-91. XIE Jun, ZENG Ding, ZHENG Xiao-hua. Long-term Deflection Prediction of Long-span Beam Bridge Based on Shrinkage Creep Self-identification[J]. Journal of Highway and Transportation Research and Development, 2013, 30(8): 88-91. |
| [7] |
BAZANT Z P, YU Qiang, LI Guang-hua, et al. Excessive Long-time Deflections of Prestressed Box Girders I:Record-Span Bridge in Palau and Other Paradigms[J]. Journal of Structure Engineering, 2012, 138(6): 676-686. |
| [8] |
BAZANT Z K P, YU Qiang, LI Guang-hua, et al. Excessive Long-time Deflections of Prestressed Box GirdersⅡ:Numerical Analysis and Lessons Learned[J]. Journal of Structure Engineering, 2012, 138(6): 687-696. |
| [9] |
ZICH M, BAZANT Z P, KOHOUTKOVÁ A, et al. Box Girder Bridge Deflections[J]. Concrete International, 2006, 28(1): 55-63. |
| [10] |
BENAIM R. The Design of Prestressed Concrete Bridges:Concepts and Principles[M]. London: Taylor & Francis Ltd., 2007.
|
| [11] |
项贻强, 何晓阳. 考虑非均匀收缩徐变的PC箱梁桥时变性能[J]. 哈尔滨工业大学学报, 2015, 47(12): 117-122. XIANG Yi-qiang, HE Xiao-yang. Time-dependent Behavior of PC Box Girder Bridges Considering Non-uniform Shrinkage and Creep[J]. Journal of Harbin Institute of Technology, 2015, 47(12): 117-122. |
| [12] |
谢峻, 王国亮, 郑晓华. 大跨径预应力混凝土箱梁桥下挠问题的研究现状[J]. 公路交通科技, 2007, 24(1): 47-50. XIE Jun, WANG Guo-liang, ZHENG Xiao-hua. State of Art of Long term Deflection for Long Span Prestressed Concrete Box girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2007, 24(1): 47-50. |
| [13] |
谢峻. 大跨径预应力混凝土箱梁桥下挠成因及对策研究[R]. 北京: 交通运输部公路科学研究院, 2010. XIE Jun. Research on Causes and Solution of Deflection of Long Span Prestressed Concrete Bridge[R].Beijing:Research Institute of Highway, MOT, 2010. |
| [14] |
钱永久, 车惠民, 余晓华. 腹板上有竖向裂缝的钢筋混凝土T梁抗剪强度试验研究[J]. 西南交通大学学报, 1994, 29(4): 385-390. QIAN Yong-jiu, CHE Hui-min, YU Xiao-hua. Experimtentai Research on Shear Strength of RC Tee Beams with Vertical Cracks on Web[J]. Journal of Southwest Jiaotong University, 1994, 29(4): 385-390. |
| [15] |
李杰, 王建鹏, 李聃. 混凝土T梁竖向裂缝对桥梁承载能力影响研究[J]. 中国水运, 2014, 14(4): 244-246. LI Jie, WANG Jian-peng, LI Dan. Study on Influence of Vertical Cracks of Concrete T-shaped Beam on Bridge Bearing Capacity[J]. China Water Transport, 2014, 14(4): 244-246. |
| [16] |
杨庆中. 钢筋混凝土T梁竖向裂缝机理分析及预防措施[J]. 中国水运, 2008, 8(10): 213-214. YANG Qing-zhong. Analysis on Vertical Cracking Mechanism and Preventive Measures for Reinforced Concrete T-shaped Beam[J]. China Water Transport, 2008, 8(10): 213-214. |
| [17] |
张铠, 曹国辉, 胡佳星. 配筋对混凝土长期收缩应变影响的试验研究[J]. 公路交通科技, 2014, 31(4): 78-81. ZHANG Kai, CAO Guo-hui, HU Jia-xing. Experimental Study on Influence of Reinforcement on Long-term Shrinkage Strain of Concrete[J]. Journal of Highway and Transportation Research and Development, 2014, 31(4): 78-81. |
| [18] |
GB50010-2010, 混凝土结构设计规范[S]. GB50010-2010, Code for Design of Concrete Structures[S]. |
 2017, Vol. 34
2017, Vol. 34
