扩展功能
文章信息
- 史杰
- SHI Jie
- 悬索桥静载试验主缆索力增量测试方法
- A Method for Measuring Main Cable Force Increment in Static Load Test of Suspension Bridge
- 公路交通科技, 2017, 34(11): 72-78
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(11): 72-78
- 10.3969/j.issn.1002-0268.2017.11.011
-
文章历史
- 收稿日期: 2016-12-06
悬索桥是以主缆为主要承重构件的桥梁,作用在桥面上的荷载由吊索传至主缆,再传至索塔和锚碇(或加劲梁端)。主缆是悬索桥重要的受力构件,因此相关公路[1-2]、市政[3]桥梁规范中悬索桥静载试验测试工况或项目中,均要求对主缆索力增量进行测试。但目前对主缆索力常用测试方法不方便于静载试验过程中使用,因此提出一种适用于静载试验主缆索力增量的测试方法。
1 常用索力测试方法的局限性目前较常用的索力测试方法即振动法。
主缆作为整体无法满足振动法的使用条件[4]。一般只能通过测试散索鞍后的分索股索力,再换算成主缆索力。有时会辅以索股锚下的压力传感器对振动法进行校正。如虎门悬索桥[5]、夏门海沧大桥[6]、佛山平胜大桥[7]、南京小龙湾大桥[8]等的静载试验中均采用该方法进行主缆索力的测试。
该方法可较好地测试主缆索力及其增量,但存在一定的不足:
(1) 主缆索股数量众多,在静载试验中有限的时间内,无法全部测量。
(2) 一般锚箱内建筑尺寸较大,在施工支架拆除后,达到索股处难度较大,甚至有可能不存在测试条件, 如自锚式悬索桥。
(3) 分索股一般一端为散索鞍,另一端则通过锚头锚板与锁紧螺母连接于拉杆,拉杆再通过锁紧螺母与锚固连接器相连,锚固连接器与锚碇中的预应力钢绞线的锚具相连[9]。分索股边界条件复杂,当无锚下压力传感器作校核时,计算索力时的合理计算长度的选取较难。
(4) 该方法在静载试验有限的时间内,仅能实现对部分分索股索力的测试,再通过有限的分索股索力,换算成主缆索力。测试得到的主缆索力误差估算,尚未见到有研究。
综上所述,振动法测试主缆索力及其增量, 存在着测试条件要求高、计算复杂等不足,因此,提出另一种较简便的间接测试方法。
2 主缆索力增量间接测试原理通过测试主塔截面在试验荷载作用下的应变,再根据结构受力分析,得到主缆索力增量与主塔截面应变增量的关系,并根据主塔截面应变增量计算得出主缆索力增量。
在下文推导中假定主缆、主塔位于同一竖直平面内,塔身应变测试截面以上为单悬臂结构,且不承受除主缆以外的其他直接作用力。
2.1 鞍座顶主缆节段受力分析主缆与主塔间力的传递是通过塔顶鞍座与主缆间的径向压力实现的,宏观上表现为主缆通过塔顶鞍座传递竖向压力及活载的水平力[10-11]。
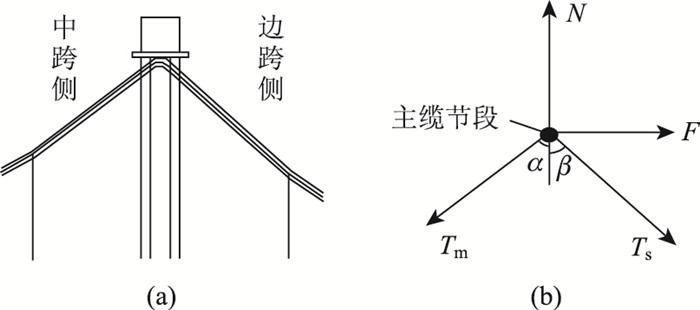
如图 1所示,取塔顶索鞍处主缆索体节段进行受力分析。主缆索体节段的力平衡方程为:
|
| 图 1 主缆节段受力分析示意图 Fig. 1 Force analysis of main cable segment |
| |
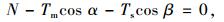
|
(1) |
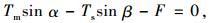
|
(2) |
式中:N为塔顶鞍座对主缆的竖向支撑力;Ts为边跨侧主缆索力;Tm为中跨侧主缆索力;F为鞍座对主缆的水平力;β为边跨侧主缆切向与竖直向夹角;α为中跨侧主缆切向与竖直向夹角。
解方程可得到:
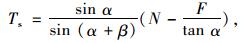
|
(3) |
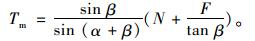
|
(4) |
由式(3)、(4),只要得到鞍座对主缆的支撑力及水平力,即可求得主缆索力。鞍座对主缆的竖向支撑力及水平力的直接测试同样是困难的。
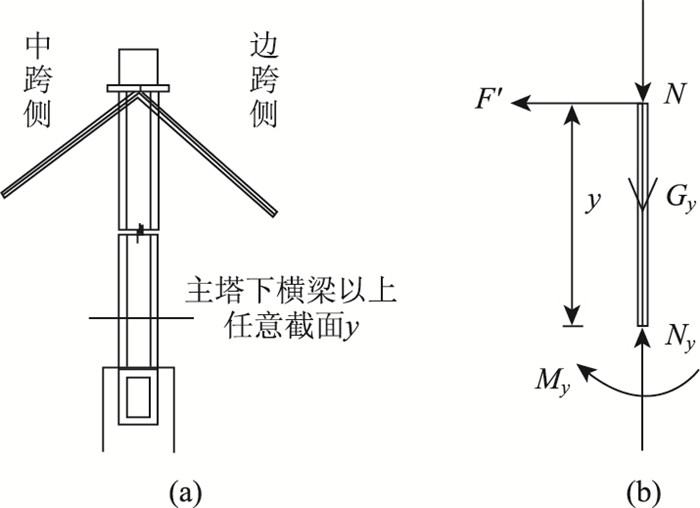
2.2 主塔节段受力分析对主塔下横梁以上任意截面y以上部分节段受力分析见图 2。截面y以上仅受到主缆作用力及自重,截面y内力可表示为:
|
| 图 2 主塔节段内力分析示意图 Fig. 2 Internal force analysis of pylon segment |
| |
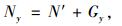
|
(5) |
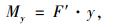
|
(6) |
式中:Ny为主塔截面y的轴力;My为主塔截面y的弯矩;Gy为主塔截面y以上塔自重;N′为主缆对塔顶鞍座的竖向压力与式(1)中的N为一对作用力与反作用力;F′为主缆对鞍座的水平力,与式(2)中的F为一对作用力与反作用力。
由式(5)、(6)可得到主缆与鞍座间作用力为:
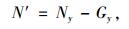
|
(7) |
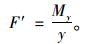
|
(8) |
主缆索力在试验荷载的作用下产生增量,同时主缆与主塔夹角也会产生微小增量,忽略该微小增量,由式(3)、(4)可得到主缆索力增量为:
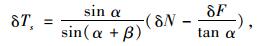
|
(9) |
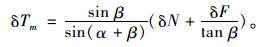
|
(10) |
由式(7)、(8)以及作用力与反作用力的关系,可得到主缆与鞍座间作用力增量为:
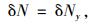
|
(11) |
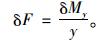
|
(12) |
因此只要测得截面y的轴力及弯矩在试验荷载作用下的增量,即可求得主缆的索力增量。根据截面内力与应变的关系[12],可得到测试截面y的轴力、弯矩增量与表面应变增量之间的关系式为:
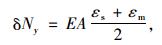
|
(13) |
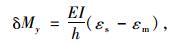
|
(14) |
式中:E为主塔混凝土弹性模量;A为主塔截面y的截面积;I为主塔截面y的抗弯惯矩;h为主塔截面y纵桥向宽度;εs为主塔截面y边跨侧实测表面应变;εm为主塔截面y中跨侧实测表面应变。
3 验证实例溪心桥位于永康市溪心路,跨越南溪,建造时为国内跨径最大的钢筋混凝土箱梁自锚式悬索桥[13],其跨径布置为(37+90+37)m,桥宽34 m,桥塔为门式钢筋混凝土结构,桥面以上和以下各设一道横梁,单根塔柱为矩形截面。
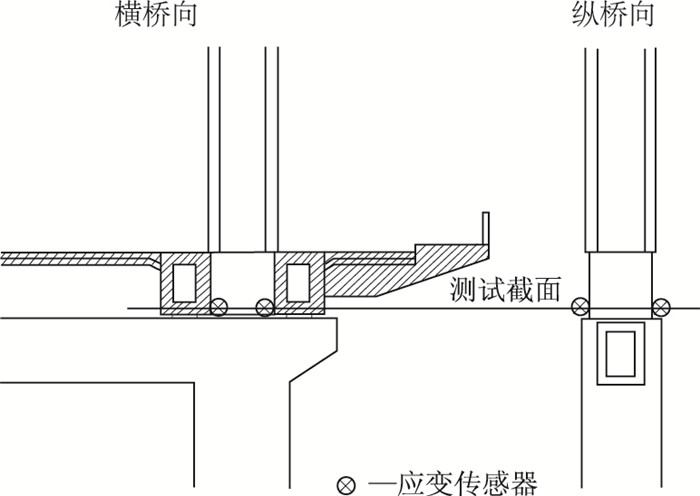
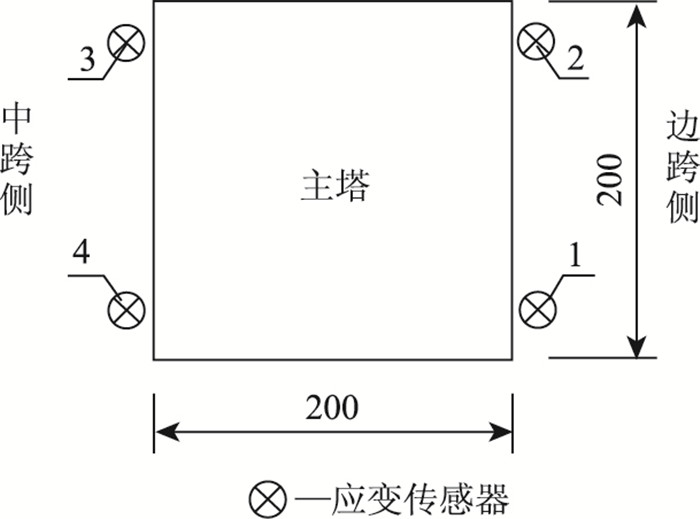
受管养单位委托对该桥进行静载试验。静载试验中设置一侧主缆最不利索力,主塔塔脚截面(位于下横梁以上,见图 3)最大弯矩的偏载工况。塔脚布设应变测点见图 4。
|
| 图 3 主塔测试截面示意图 Fig. 3 Test section of pylon |
| |
|
| 图 4 主塔应变测点布置图(单位:cm) Fig. 4 Arrangement of strain monitoring points (unit:cm) |
| |
因上横梁刚度较小,试验中假设下横梁以上两塔柱为单独受力。表 1给出了偏载侧塔脚的应变测试结果。由表可得到:
| 测点位置及编号 | 边跨侧表面测点 | |||
| 1 | 2 | 3 | 4 | |
| 实测应变/με | 25.6 | — | -54.5 | -48.1 |
| 平均应变/με | 25.6 | -51.3 | ||
| 理论应变/με | 35.7 | -70.2 | ||
| 校验系数 | 0.72 | 0.73 | ||
| 注:②测点因导线损坏,为无效测点。 | ||||
εs=25.6 με, εm=-51.3 με。
塔柱材料及测试截面特性暂按设计值取用:
E=3.25×107 kPa,
A=4 m2, I=1.333 3 m4。
塔顶主缆距测试截面竖直距离y=21.946 m,塔顶处主缆切向与竖直向的夹角为:
α=52.86°,β=50.40°。
由式(13)、(14)可求得:
δNy=1 670.5 kN,δMy=1 666.2 kN·m。
由式(11)、(12)可求得:
δN=1 670.5 kN,δF=75.9 kN。
由式(9)、(10)可求得塔顶边、中跨侧主缆索力增量为:
δTs=1 321.0 kN,δTm=1 372.1 kN。
通过间接法测试主缆索力校验系数见表 2,边、中跨侧主缆索力校验系数均为0.71,这与表 1中主塔测试截面应变校验系数相当,表明间接法换算得到的主缆索力的正确性。
| 主缆位置 | 边跨侧主缆 | 中跨侧主缆 |
| 实测索力增量/kN | 1 321.0 | 1 372.1 |
| 计算索力增量/kN | 1 868.5 | 1 938.2 |
| 校验系数 | 0.71 | 0.71 |
4 测试方法影响因素分析
上文中索力增量公式的推导及验证实例的测量中均做了一定的假设,均可能对测量结果产生影响。同时应变计的测试精度也会对测试结果产生影响。因此有必要对影响索力增量测试的影响因素进行分析,确定主要因素,提高测试精度。
4.1 主缆倾角加载过程中变化量影响悬索桥为大位移几何非线性结构体系。恒载所产生主缆拉力占总拉力的85%以上,巨大的恒载作用在主缆上,形成全桥的重力刚度[10]。主缆线形也是根据桥梁恒载确定的,在活载作用下主缆切线与竖直向的夹角变化也很小。
验证实例中,计算分析表明在试验荷载作用下偏载侧主塔塔顶转角:δ=3.9″远小于主缆切向与竖直向的夹角,因此主缆倾角在加载前后的变化量是微小量,可忽略该变化量对测试结果的影响。
4.2 上横梁横向传力对测试结果的影响因静载试验实施前认为上横梁刚度较小,两塔柱间直接传递力值较小,进而假设下横梁以上两塔柱间独自受力。因此并未在非偏载侧塔柱布设应变测点。
可从理论计算模型分析上横梁横向传力对测试结果的影响。建立溪心桥实桥模型1,取消塔柱间上横梁建立模型2。分析在试验荷载作用下,有无上横梁对主缆索力(目标值)及塔脚内力(测试值)的影响。
分析结果见表 3,显示有无上横梁,偏载侧主缆、塔脚内力误差均不超过3%;非偏载侧略大,但不超过10%;两侧主缆及塔脚合力误差接近于0。因此塔柱间上横梁对偏载侧主缆索力影响较小,测试偏载侧主缆索力增量时,可忽略其横桥向传力影响。
| 构件/位置 | 模型1 | 模型2 | 相差/% | ||
| 偏截侧 | 主缆索力/kN | 中跨侧 | 1 938.2 | 1 918.6 | -1.0 |
| 边跨侧 | 1 868.5 | 1 917.9 | 2.6 | ||
| 塔脚内力 | 轴力/kN | -2 227.1 | -2 248.7 | 1.0 | |
| 弯矩/(kN·m) | -2 286.0 | -2 313.9 | 1.2 | ||
| 非偏截侧 | 主缆索力/kN | 中跨侧 | 460.8 | 480.5 | 4.3 |
| 边跨侧 | 516.6 | 466.6 | -9.7 | ||
| 塔脚内力 | 轴力/kN | -574.9 | -553 | -3.8 | |
| 弯矩/(kN·m) | -765.4 | -736.2 | -3.8 | ||
| 合计 | 主缆索力/kN | 中跨侧 | 2 399.0 | 2 399.1 | 0.0 |
| 边跨侧 | 2 385.1 | 2 384.5 | 0.0 | ||
| 塔脚内力 | 轴力/kN | -2 802.0 | -2 801.7 | 0.0 | |
| 弯矩/(kN·m) | -3 051.4 | -3 050.1 | 0.0 | ||
| 注:(1)主缆索力、塔脚轴力均以受拉为正,受压为负;(2)模型1为原桥模型,模型2为取消上横梁的模型。 | |||||
4.3 应变测试精度的影响
上文中索力增量公式的推导中,塔脚应变是直接测量,其测试的误差对结果影响可由下式计算。
将(11)~(14)式代入(9)、(10)式可得:
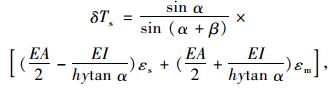
|
(15) |
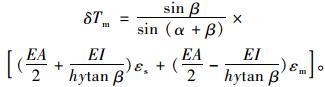
|
(16) |
利用全微分在近似计算中的应用[14],可得到由应变测量误差引起的主缆索力误差公式为:
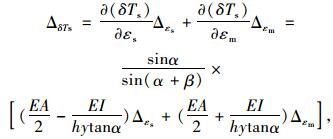
|
(17) |
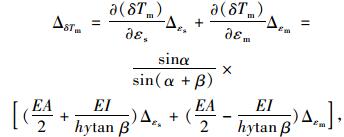
|
(18) |
式中, ΔδTs为边跨侧主缆索力测试误差;ΔδTm为中跨侧主缆索力测试误差;Δεs为主塔测试截面边跨侧应变测试误差;Δεm为主塔测试截面中跨侧应变测试误差。
应变计种类较多,如电阻式应变片、千分表引伸计、振弦式应变计等[15]。种类不同,其测试精度也有差别。表 4中给出了验证实例中应变测试精度引起的索力增量误差表,当应变精度超过2 με时,引起的索力增量误差已超过15%。因此实测时,宜采用高精度的应变计。
| Δε/με | 0.1 | 0.5 | 1 | 2 | 3 | |
| 绝对误差/kN | δTm | 10.3 | 51.5 | 102.9 | 205.8 | 308.7 |
| δTs | 10.6 | 53.2 | 106.5 | 212.9 | 319.4 | |
| 相对误差/% | δTm | 0.8 | 3.8 | 7.5 | 15 | 22.5 |
| δTs | 0.8 | 4.0 | 8.06 | 16.12 | 24.18 | |
4.4 塔柱混凝土弹性模量的影响
验证实例中采用混凝土设计弹性模量进行主缆索力增量的计算,但混凝土弹性模量是一个随时间变化的量, 宜采用实测弹性模量进行计算。而一般桥梁检测中对混凝土进行弹性模量的测试是困难的;国内桥涵规范[16-17]中也未作明确规定,因此参考CEB-FIP[18]规范中提供的混凝土弹性模量随时间发展公式进行估算。
CEB-FIP提供的弹性模量随时间发展公式如下:
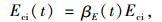
|
(19) |
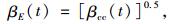
|
(20) |
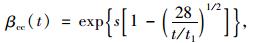
|
(21) |
式中,Eci(t)为材龄为t时的混凝土弹性模量;βE(t),βcc(t)为与时间有关的计算参数;Eci为混凝土28 d弹性模量;s为水泥种类系数,普通混凝土s=0.25;t为混凝土龄期;t1=1 d。
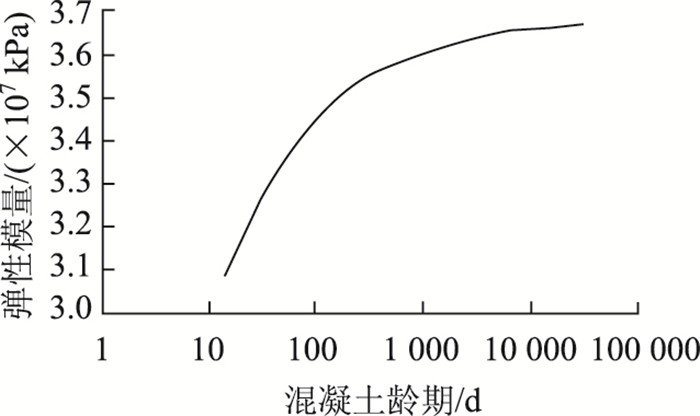
可计算出验证实例中主塔C40混凝土的弹性模量发展曲线见图 5。
|
| 图 5 混凝土弹性模量随时间变化曲线 Fig. 5 Curve of elastic modulus of concrete varying with time |
| |
试验时该桥已建成约8 a(2 920 d),主塔混凝土弹性模量估算值为:
Eci(2 920 d)=3.64×107 kPa
由弹性模量引起的主缆索力增量误差见表 5。混凝土弹性模量后期增长约12.0%,索力相差了11.9%。因此采用该方法时宜对混凝土进行弹性模量的测试或采用经验曲线进行修正。
| 测试位置 | 边跨侧主缆 | 中跨侧主缆 |
| E=3.25×107 kPa | 1 321.0 kN | 1 372.1 kN |
| E=3.64×107 kPa | 1 478.7 kN | 1 535.5 kN |
| 相差/% | 11.9 | 11.9 |
4.5 几何参数误差的影响
结构的几何参数如主塔截面特性,塔顶两侧主缆与竖直向的夹角等均会对计算索力增量产生影响。
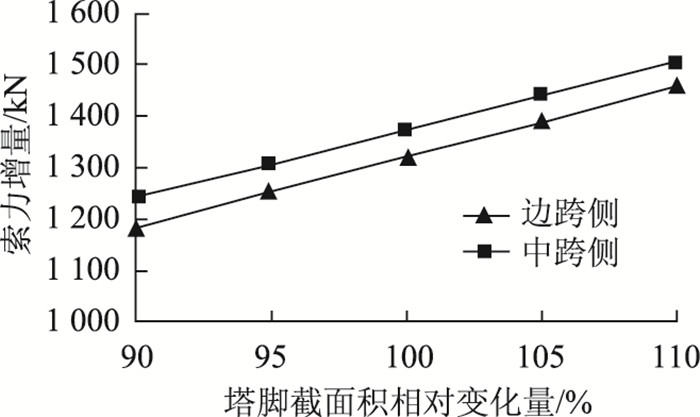
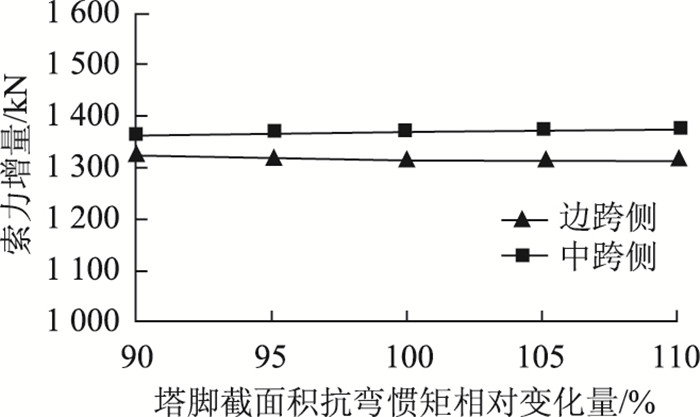
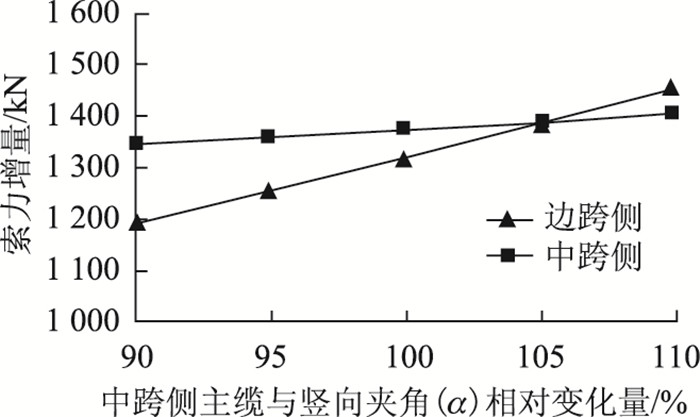
以验证实例为基本参数,分别考虑主塔截面积、抗弯惯矩、中跨侧主缆与竖向夹角(α)、边跨侧主缆与竖向夹角(β)变化±10%时,计算各参数对索力增量测试的影响,分别见图 6~图 9。
|
| 图 6 塔脚截面面积误差对索力增量的影响 Fig. 6 Influence of pylon foot section area error on cable force increment |
| |
|
| 图 7 塔脚截面抗弯惯矩误差对索力增量的影响 Fig. 7 Influence of pylon foot section bending moment on cable force increment |
| |
|
| 图 8 中跨侧主缆与竖向夹角误差对索力增量的影响 Fig. 8 Influence of angle error between mid-span cable's tangential direction and vertical direction on cable force increment |
| |
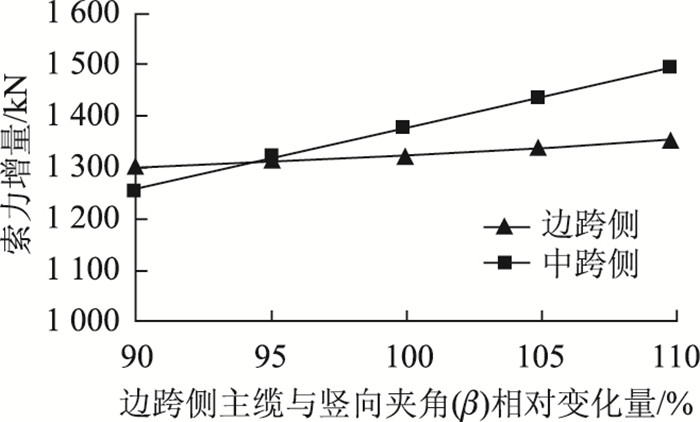
|
| 图 9 边跨侧主缆与竖向夹角误差对索力增量的影响 Fig. 9 Influence of angle error between side-span cable's tangential and direction and vertical direction on cable force increment |
| |
图示表明除塔脚截面抗弯惯矩对主缆索力增量计算误差影响较小;塔脚截面积误差对两侧索力增量的测试影响均较大;而边/中跨侧主缆与竖向夹角的误差会对中/边跨侧索力增量的产生较大的影响,均不可忽略。因此应用该方法时,宜对桥梁主要结构尺寸进行复测确认。
5 结论提出一种新的适用于静载试验中悬索桥主缆索力增量测试的间接方法。即通过测试主塔特定截面的应变增量,利用结构的材料、几何参数,根据结构受力关系,计算出主塔顶两侧主缆索力增量。将该方法应用到溪心桥静载试验中,得到较好的效果。结合实例对影响主缆索力增量测试精度的各因素进行了分析,提出应变测试精度、塔柱的材料特性、截面积及塔顶主缆切向与竖直向的夹角对测试结果均有较大的影响。该方法实施简单、方便,对仪器设备及测试条件要求较低, 可为同类桥梁在静载试验中进行主缆索力增量测试提供参考。
| [1] |
JTG/T J21-2011, 公路桥梁承载能力检测评定规程[S]. JTG/T J21-2011, Specification for Inspection and Evaluation of Load-bearing Capacity of Highway Bridge[S]. |
| [2] |
JTG/T J21-01-2015, 公路桥梁荷载试验规程[S]. JTG/T J21-01-2015, Load Test Methods for Highway Bridge[S]. |
| [3] |
CJJ/T 233-2015, 城市桥梁检测与评定技术规范[S]. . CJJ/T 233-2015, Technical Code for Test and Evalua-tion of City Bridges[S] |
| [4] |
张劲泉, 李承昌, 郑晓华, 等. 桥梁拉索与吊索[M]. 北京: 人民交通出版社, 2013. ZHANG Jin-quan, LI Cheng-chang, ZHENG xiao-hua, et al. Inhaul Cable and Suspender of Bridge[M]. Beijing: China Communications Press, 2013. |
| [5] |
张劲泉, 赵仲华, 花迎春. 虎门悬索桥交工验收静力荷载试验与评价[J]. 公路交通科技, 2000, 17(5): 31-34. ZHANG Jin-quan, ZHAO Zhong-hua, HUA Ying-chun. Static Loading Test and Assessment for Completion Acceptance of Humen Suspension Bridge[J]. Journal of Highway and Transportation Research and Development, 2000, 17(5): 31-34. |
| [6] |
谌润水, 胡钊芳. 公路桥梁荷载试验[M]. 北京: 人民交通出版社, 2003. CHEN Run-shui, HU Zhao-fang. Load Test of Highway Bridge[M]. Beijing: China Communications Press, 2003. |
| [7] |
柯红军, 李传习, 刘建. 平胜大桥自锚式悬索桥静载试验与评价[J]. 公路交通科技, 2009, 26(2): 53-59. KE Hong-jun, LI Chuan-xi, LIU Jian. Static Loading Test and Assessment of Pingsheng Self-anchored Suspension Bridge[J]. Journal of Highway and Transportation Research and Development, 2009, 26(2): 53-59. |
| [8] |
郭霖华, 端茂军, 刘贝. 南京小龙湾大桥荷载试验方案设计与分析[J]. 南京工程学院学报:自然科学版, 2013, 11(3): 17-22. GUO Lin-hua, DUAN Mao-jun, LIU Bei. Design and Analysis of Loading Tests on Nanjing Xiaolongwan Bridge[J]. Journal of Nanjing Institute of Technology:Natural Science Edition, 2013, 11(3): 17-22. |
| [9] |
许汉铮, 黄平明, 杨炳成. 大跨径悬索桥静载试验研究[J]. 公路, 2003(9): 1-7. XU Han-zheng, HUANG Ping-ming, YANG Bing-cheng. Research on Static Load Test of Long Span Suspension Bridge[J]. Highway, 2003(9): 1-7. |
| [10] |
孟凡超. 悬索桥[M]. 北京: 人民交通出版社, 2011. MENG Fan-chao. Suspension Bridge[M]. Beijing: China Communications Press, 2011. |
| [11] |
张哲. 混凝土自锚式悬索桥[M]. 北京: 人民交通出版社, 2005. ZHANG zhe. Concrete Self-anchored Suspension Bridge[M]. Beijing: China Communications Press, 2005. |
| [12] |
孙训方, 方孝淑, 关来泰. 材料力学(Ⅰ)[M]. 北京: 高等教育出版社, 2002. SUN Xun-fang, FANG Xiao-shu, GUAN Lai-tai. Mechanics of Materials (Ⅰ)[M]. Beijing: Higher Education Press, 2002. |
| [13] |
魏华, 陈妙统, 徐栋. 国内最大跨径钢筋混凝土主梁自锚式悬索桥——永康市溪心桥施工控制[J]. 结构工程师, 2004, 20(3): 77-82. WEI Hua, CHEN Miao-tong, XU Dong. Construction Control of the Xixin Bridge:The Longest Span Reinforced Concrete Girder Self-anchored Suspension Bridge in China[J]. Structural Engineers, 2004, 20(3): 77-82. |
| [14] |
同济大学数学教研室. 高等数学[M]. 北京: 高等教育出版社, 1996. Maths Staff Room of Tongji University. Advanced Mathematics[M]. Beijing: Higher Education Press, 1996. |
| [15] |
何玉珊, 程崇国, 章关永, 等. 公路水运工程试验检测专业技术人员职业资格考试用书-桥梁隧道工程[M]. 北京: 人民交通出版社, 2016. HE Yu-shan, CHENG Chong-guo, ZHANG Guan-yong, et al. Vocational Qualification Examinations Book for Professionals Engaged in Test and Detection of Highway Engineering and Port & Waterway Engineering:Bridge and Tunnel Engineering[M]. Beijing: China Communications Press, 2016. |
| [16] |
JTG D62-2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62-2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [17] |
TB10002. 3-2005, 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S]. TB10002.3-2005, Code for Design on Reinforced and Prestressed Concrete Structure of Railway Bridge and Culvert[S]. |
| [18] |
Comite Euro-internation Du Beton. CEB-FIP Model Code 1990[M]. London: Thomas Telford Services Ltd, 1993.
|
 2017, Vol. 34
2017, Vol. 34
