扩展功能
文章信息
- 童潇, 冯仲仁
- TONG Xiao, FENG Zhong-ren
- 客家大桥体系转换过程中悬臂端挠度变化的影响因素分析
- Analysis on Factors Influencing on Deflection of Cantilever End during Hakka Bridge System Conversion Process
- 公路交通科技, 2017, 34(11): 64-71, 78
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(11): 64-71, 78
- 10.3969/j.issn.1002-0268.2017.11.010
-
文章历史
- 收稿日期: 2016-08-18
预应力混凝土变截面连续梁桥采用悬臂施工,在悬臂施工阶段结束后,再进行各合龙段及体系转换的施工。对于多跨连续梁桥而言,通常按照先边跨,后次中跨,最后中跨的顺序进行[1-2]。悬臂施工过程中,为保证成桥线形,需设置相应的施工预拱度。影响施工预拱度的因素主要包括一期恒载、预应力、二期恒载、结构体系转换、混凝土徐变等。为保证桥梁结构在成桥状态下的线形及受力满足设计要求,学者对体系转换进行了大量研究分析。张文学等[3]建立了3种悬臂施工临时固结结构的分析计算模型,对临时固结结构进行研究,并推导出相应的设计计算公式。吴志和等[4]利用Midas-civil有限元软件对墩梁临时固结体系采用不同的方式进行模拟,分析了对主梁变形的影响。林晓威[5]、曾振华等[6]、陈荣刚[7]发现,不同的合龙方案和体系转换步骤对主桥分段施工的预拱度影响很大,结构体系转换顺序对主梁施工预拱度的设置影响最为显著,而陈金水[8]、包仪军等[9]还讨论了其对桥梁内力分布与成桥线形产生的不同影响。陈宇、王铭等[10-11]分别对连续钢构桥和T梁桥的临时固结和边界条件进行分析,探讨了其对挠度与线型的影响。在对江西省赣州市客家大桥的施工监控过程中,却发现悬臂端的端高程呈现出先降后升(最终整体效果仍为下降)的现象。这一现象在其他桥梁施工中也出现过,是体系转换过程中比较常见的工程现象,故本研究针对这一工程实际问题,以客家大桥为研究背景,探究其成因,从结构受力和变形两个方面进行研究分析。
1 工程概况 1.1 临时固结方式结构体系转换中的关键工序即拆除主梁与桥墩之间的临时支撑结构,常见的临时固结方式一般有以下几类:
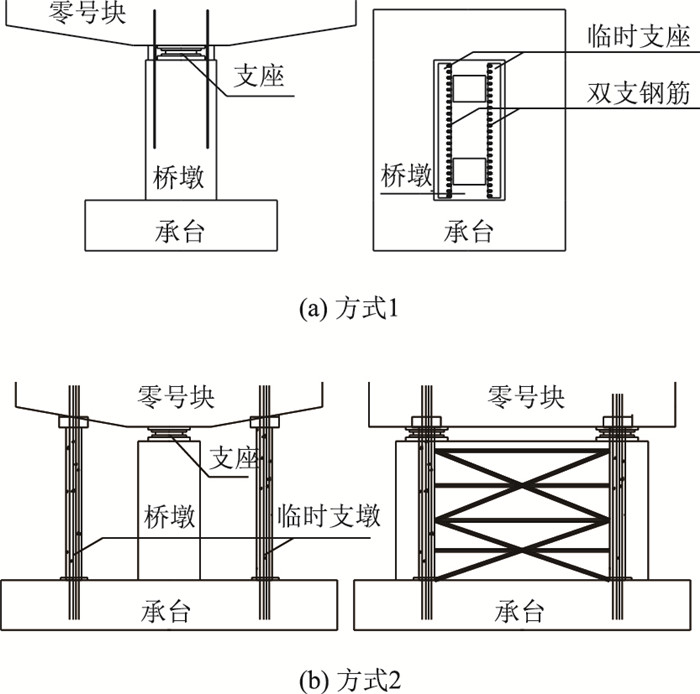
(1) 在墩顶与主梁0#块之间设置临时条形支墩和预应力粗钢筋[12]。这种方式是通过混凝土临时支座和双排粗钢筋构成的临时固结体系来承受悬臂施工中的不平衡弯矩,见图 1(a)。其特点是支座间距小,抗压刚度大,主要适用于墩身尺寸较大,易于在墩顶设置支撑,且结构跨径不太大的情况。
|
| 图 1 临时固结示意图 Fig. 1 Schematic diagram of temporary consolidation system |
| |
(2) 在承台和0#块之间设置临时支墩[12]。通常采用钢管混凝土或钢筋混凝土立柱。穿过支墩的预应力钢筋连接承台与梁底,下端锚固在基础承台内,上端在0#块底板张拉、锚固,保证临时支座结构在悬臂施工过程中始终处于受压状态,见图 1(b)。因钢管混凝土柱性能受长细比影响较大,故常用于桥梁墩身比较矮小、0#块较长的情况下。
(3) 采用扇形或门式托架支撑主梁0#块,同时在墩顶设置支墩[12-13],用以平衡主梁悬臂施工期间的不平衡荷载。这种支承方式受力体系最为复杂,常用于桥梁墩身比较矮小、墩顶有一定空间可设置临时支墩及可安装墩侧临时支撑的桥梁结构。
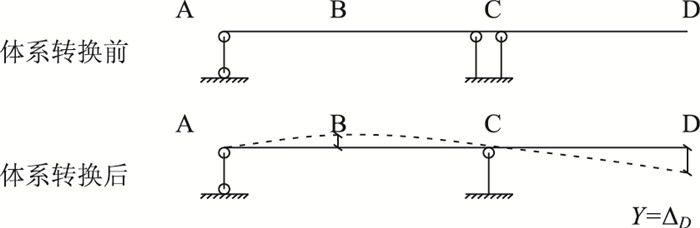
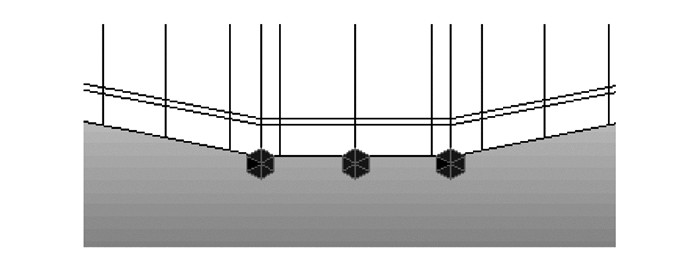
1.2 工程背景江西省赣州市客家大桥长(85+3×138+85)m,分左右两幅,采用挂篮悬浇施工。各墩悬臂施工共17个节段,0#块长17 m,最大悬臂长68 m,合龙段长2 m,采用第1种临时支承方式,利用Midas-civil建立全桥模型,如图 2所示。在边跨合龙段施工结束后,需进行体系转换,解除0#块临时支墩,主梁在C点处与桥墩由刚接转换为铰接,见图 3。体系转换结束后,根据模型分析结果,D点挠度ΔYD=37 mm。体系转换前,用两个固定铰支座(Midas-civil模型中以刚性连接和对下方节点释放y轴旋转刚度来模拟,如图 4所示)模拟墩梁临时固结,用一个固定铰支座(模型中下方节点固结)模拟永久支座[14],如图 5所示。

|
| 图 2 客家大桥Midas-civil模型 Fig. 2 Midas-civil model of Hakka Bridge |
| |
|
| 图 3 体系转换示意示意图 Fig. 3 Schematic diagram of system conversion |
| |
|
| 图 4 支座下方节点固结方式示意图 Fig. 4 Schematic diagram of consolidation mode of nodes below support |
| |
|
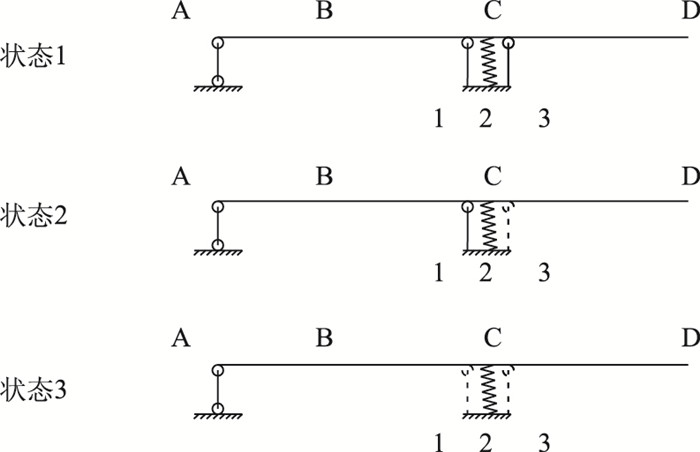
| 图 5 施工过程中体系转换过程示意图 Fig. 5 Schematic diagram of system conversion process |
| |
由于临时支座的构造形式,使得其在拆除过程中存在着先后次序。根据客家大桥施工顺序,其过程如下(被拆除构件的以虚线表示):
(1) 初始体系,定义为状态1。
(2) 解除3,体系稳定后,定义为状态2。从状态1到状态2为步骤Ⅰ;步骤Ⅰ在Midas-civil模型中为钝化刚性连接3,其余不变。
(3) 解除1,体系稳定后,定义为状态3;从状态2到状态3为步骤Ⅱ。步骤Ⅱ在Midas-civil模型中为钝化刚性连接1,并同时激活刚性连接2。
1.3 临时支座验算客家大桥采用第1种临时固结方式,当单侧临时支座承担所有荷载时,其压缩量为:
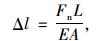
|
(1) |
式中,Δl为永久支座压缩量;Fn为结构全部荷载;L为临时支座高;E为混凝土弹性模量;A为单侧临时支座面积。
取Fn=8 000 kN,L=0.5 m,E=3.35×104 N/mm2,A=8.5×0.5=4.25 m2, 得:
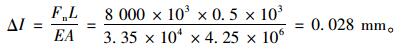
|
当临时支座与永久支座间距增加,考虑实际施工等因素,通常采用第2种临时固结体系时,以高H=10 m,钢管外径D=800 mm,壁厚t=12 mm,C50混凝土,钢材型号Q235为例计算,得到钢管混凝土结构承载能力为:
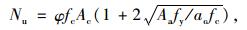
|
(2) |
式中,fc为混凝土强度设计值;fy为钢筋强度设计值;长细比影响系数φ=0.665;钢管横截面积Aa=30 159.29 mm2;核心混凝土面积Ac=502 654.82 mm2。得:Nu=1.912×104 kN。
施工中通常单侧采用两根钢管混凝土柱,拆除悬臂端侧支撑结构之前,单根柱构件承受荷载为8 000/4=2 000 kN,拆除之后,荷载为4 000 kN,增量为2 000 kN。若钢管厚度增大,构件数量增加,则单根柱荷载减小。此外,永久支座已参与结构受力,荷载增量愈加小,这点从下文中支座反力分析中也可得到印证。因此,结构增加的压缩变形量同样可以忽略不计。另外,通过对悬臂端的观测,发现在边跨合龙段预应力钢束张拉以后,其高程并未发生明显变化,可见临时固结体系刚度之大。故上文中临时支墩以铰接模拟的方式适用于本模型。
2 体系转换过程分析 2.1 实测数据记录体系转换过程中悬臂端挠度变化过大,往往是造成合龙段两侧高程相对误差过大的重要因素之一。如果为了结构线形而采取强制措施合龙,又必然容易导致结构内力与设计值不符,影响结构的安全性能。在对客家大桥体系转换过程的监控中,得到4组数据,见表 1。步骤Ⅰ悬臂端挠度为-66 mm(挠度向上为正,向下为负,下同),步骤Ⅱ挠度为29 mm。现针对这一现象,对客家大桥体系转换过程进行分析,寻找引起悬臂端挠度剧烈变化的因素,分析其影响方式。
| 组别 | D点挠度/mm | ||
| 步骤Ⅰ | 步骤Ⅱ | 总计 | |
| 1 | -68 | 30 | -38 |
| 2 | -66 | 29 | -37 |
| 3 | -63 | 27 | -36 |
| 4 | -67 | 31 | -36 |
| 均值 | -66 | 29.25 | -36.75 |
状态1时,临时支座1和3承受全部荷载,永久支座2受力非常小,可认为不受力。经过步骤Ⅰ,在状态2时,C点、D点挠度向下,永久支座开始参与受力,并随着C点向下的挠度增加而增大。现将支座2模拟为弹性支撑,并增加主梁顺桥向水平约束,以控制x方向的位移。
2.2 确定影响因素运用因素分析法及叠加原理对步骤Ⅰ、步骤Ⅱ中的结构变形拆分。方案如表 2所示。通过对比模型a与b,可得出在结构形式完全相同时,结构支点从支座1移动到支座2(或从支座2移动到支座1)时悬臂端的挠度值变化;对比分析模型a(a1-a2)和c(c1-c3),可以分析永久支座弹性系数对悬臂端挠度的影响;对比分析模型b和c,可以分析永久支座在状态2下在结构中的参与度。根据盆式橡胶支座参数文件可以查阅得到:在竖向设计荷载下,支座压缩变形值不超过2%,支座高度为30 cm,则理论最大压缩量为6 mm。通过实际工程测量得到墩顶0#块中心的基准测量点在体系转换前后高程下降5 mm,据此调整模型中模拟永久支座的弹性连接与实际相符。
| 组别 | 结构状态 | 支座1 | 支座2 | 支座3 |
| 模型a | a1 | 铰 | - | 铰 |
| a2 | - | 铰 | - | |
| 模型b | b1 | 铰 | - | 铰 |
| b2 | 铰 | - | - | |
| 模型c | c1 | 铰 | 弹 | 铰 |
| c2 | 铰 | 弹 | - | |
| c3 | - | 弹 | - | |
| 注:“a1”、“a2”等表示不同模型的不同施工状态,“铰”、“弹”及“-”表示模型中该支座处采用固定支座、弹性支撑或不设置任何连接。 | ||||
根据以上方案,对比模型调整后得出的数据,拆分分析过程见表 3、表 4。
 |
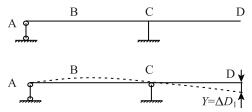
①释放y轴的转动约束,D点挠度ΔD1=-30 mm。 |
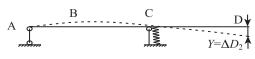 |
②支点向A点侧移动,悬臂长度增加,D点挠度ΔD2=-37 mm;通过计算,1支座压缩量可忽略。 |
| 注:挠度变化值向上为正,向下为负,下同。 | |
 |
③支点前移,施工过程中对应解除1,D点挠度ΔD3=38 mm。 |
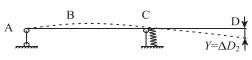 |
④支座压缩变形,支座从不受荷载(或受力很小)到承担主要荷载,支座弹性变形,C点下降,D挠度ΔD4=-9 mm。 |
表 3中①和②即对步骤Ⅰ的拆分分析。D点在步骤Ⅰ中的挠度由①和②叠加而成,为ΔD1+ΔD2;其中①过程由于边跨合龙段B处预应力产生的上拱效应,C点顺时针旋转,D点下挠。由此可以判定,当临时支座1与3共同作用时,墩梁固结处的实际支点应并不在永久支座上,而是在永久支座偏向悬臂端一侧,具体位置需通过支座反力进行论证,即在过程①中,该支点已经发生移动。过程②表示支点向A端移动,在这一状态中,永久支座2受到的作用力比较小。
从过程①到过程④,是结构体系转换的全过程拆分分析。体系转换过程结束后,D点总挠度为:
ΔD=ΔD1+ΔD2+ΔD3+ΔD4=-38 mm。
通过以上拆分分析可以发现,在理想条件下,②和③互为逆过程。而ΔD2+ΔD3=-37+38=1 mm≈0,则根据对比模型分析得出的数据与工程实测数据,可以认为本模型能够有效地反映工程实际受力状态,故以下基于模型的分析过程和由此得出的结论可认为合理有效。
综合以上对步骤Ⅰ和步骤Ⅱ过程的分析,可以发现,相对于状态1而言,状态3的变形和位移可认为由3部分组成:Y=Y1+Y2+Y3。
Y1:C点处由刚接变铰接,产生顺时针转角位移,D下降,B上升,悬臂端挠度Y1=ΔD1。
Y2:支点由偏向支座3一侧逐渐移动到永久支座上,悬臂端挠度Y2=ΔD2+ΔD3。
Y3:C点永久支座压缩,B点和D点按比例相应下挠,悬臂端挠度Y3=ΔD4。
3 影响悬臂端挠度的因素分析结构跨径、断面尺寸、预应力钢束的布置等一旦确定,过程①因边跨预应力上拱造成D点的挠度也就确定。而解除临时固结体系的整个施工过程持续时间仅为3 d左右,期间没有发生剧烈的温度变化,所以在本模型中不考虑温度对其的影响。故在体系转换过程中影响悬臂端挠度的原因有两部分:一是支点移动的距离;二是永久支座的弹性系数。支座对于悬臂端的影响可根据相似三角形原理确定。支座的选择取决于结构自身重量,支座弹性系数越大,悬臂端挠度越小。故结构支点的往返移动是造成悬臂端挠度先增大后减小的关键因素,而支点移动的距离是由临时支座与永久支座的距离决定的,故最终的决定性因素为临时支座与永久支座的距离。
3.1 方案设计客家大桥零号块长17 m,故0<d<8.5(d为永久支座到一侧临时支座的距离)。对于这类临时固结方式,考虑实际施工的影响,d最小取值0.5 m,最大取值8 m。客家大桥选定的临时支座与永久支座距离为1.5 m,现增加0.5,1,2,3,4,5,6,7,8 m等距离,共10组数据。对应修改Midas-civil模型中的距离,运行模型,提取相关数据,作数据对比分析。
3.2 数据提取与分析 3.2.1 支座反力分析通过以上对比方案,运行模型得到10组数据,对各个状态下各支座的反力进行分析。状态1时根据模型提取支座反力Ri(i取A, 1, 2, 3)数据如表 5所示,绘制图 6。其中,支座2反力为零。
| 距离/m | 支座反力/kN | ||
| 支座A | 支座1 | 支座3 | |
| 0.5 | 619.8 | 1 418.3 | 6 591.4 |
| 1 | 626.6 | 2 512.7 | 5 490.5 |
| 1.5 | 626.4 | 2 908.8 | 5 093.8 |
| 2 | 630.7 | 3 168.8 | 4 830.3 |
| 3 | 632.5 | 3 420.7 | 4 576.4 |
| 4 | 632.1 | 3 545.0 | 4 452.0 |
| 5 | 633.1 | 3 627.4 | 4 368.6 |
| 6 | 635.2 | 3 688.3 | 4 306.2 |
| 7 | 634.6 | 3 723.2 | 4 271.4 |
| 8 | 635.6 | 3 765.5 | 4 227.8 |
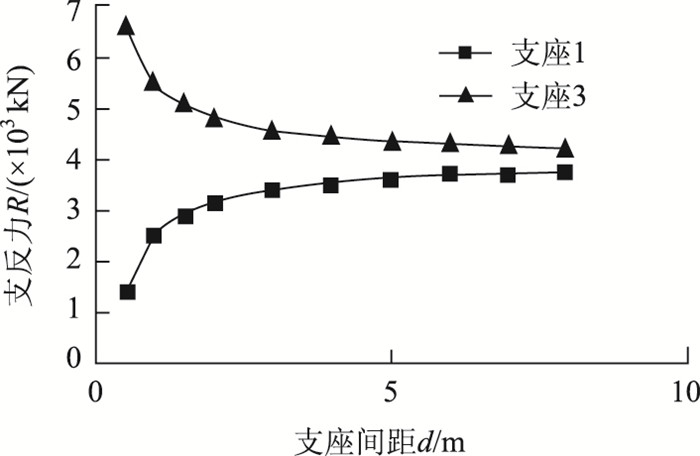
|
| 图 6 状态1时支座反力变化趋势图 Fig. 6 Curves of support reaction of state 1 |
| |
从图 6可以看出,在状态1时,随着d的增大,R1增大,R3减小。当d较小时,曲线斜率大,R变化快;随着d的增大,斜率逐渐减小,R变化愈来愈小,R1-R3差值逐渐减小,实际支点越趋近于中点处;而结构总重量一定,RA越大,R1+R2则逐渐减小。当d增加到一定程度后,差值趋于稳定。另外,d越大,对于此类临时固结结构(配筋、截面尺寸等)而言,刚度越大,抗扭转性能越强,承受施工过程中的不平衡荷载的能力也越强,对施工控制更有利。其变化趋势可拟合成以下指数类函数式。
由R1的变化趋势拟合成指数函数:
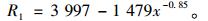
|
(3) |
由R3的变化趋势拟合成指数函数:
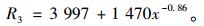
|
(4) |
将x=1.5 m代入式(3)和式(4), 得:
R1=2 949.17 kN;R3-5 033.24 kN。
支座支反力偏差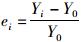
| 距离/m | e1/% | e3/% |
| 0.5 | -6.15 | 1.12 |
| 1 | 0.21 | -0.43 |
| 1.5 | -0.99 | 0.21 |
| 2 | 0.24 | -0.48 |
| 3 | -0.15 | -0.17 |
| 4 | -0.09 | -0.20 |
| 5 | -0.19 | -0.08 |
| 6 | -0.37 | 0.13 |
| 7 | -0.24 | 0.03 |
| 8 | -0.56 | 0.36 |
从表 6可看出,由模型分析得到的数据和拟合函数计算得到的数据偏差,除0.5 m处以外,其余点误差均在1%以内,说明此模拟函数基本合理,通过此拟合函数计算得到的其他距离下的支座反力值具有一定可信力,能够满足本研究涉及到的模型的理论计算要求。
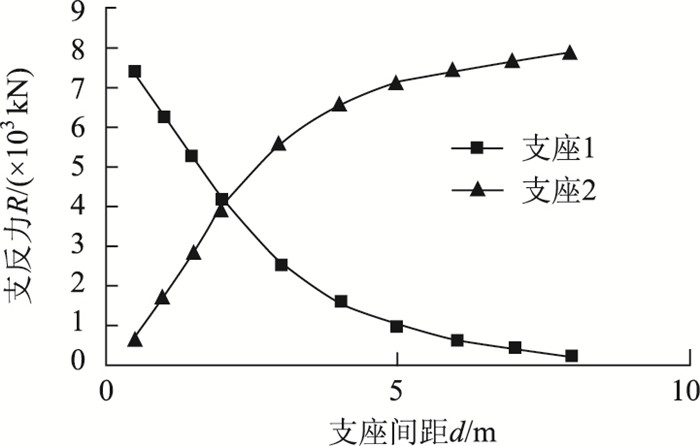
状态2时支座2开始参与到结构体系的受力中,对其各支座反力提取数据记录如表 7所示,并由此生成支座反力变化趋势图,见图 7。
| 距离/m | 支座反力/kN | ||
| 支座A | 支座1 | 支座2 | |
| 0.5 | 545.6 | 7 386.3 | 697.0 |
| 1 | 516.3 | 6 362.8 | 1 750.8 |
| 1.5 | 505.8 | 5 292.4 | 2 830.8 |
| 2 | 493.1 | 4 165.0 | 3 971.8 |
| 3 | 500.1 | 2 579.3 | 5 550.2 |
| 4 | 514.1 | 1 592.3 | 6 522.8 |
| 5 | 529.7 | 1 009.8 | 7 089.5 |
| 6 | 544.6 | 660.5 | 7 424.6 |
| 7 | 554.9 | 416.1 | 7 658.2 |
| 8 | 569.0 | 201.5 | 7 858.4 |
|
| 图 7 状态2时支座反力变化趋势图 Fig. 7 Curves of support reaction of state 2 |
| |
在经步骤Ⅰ后,状态2时,根据表格中数据拟合出的支座反力与距离的函数R1和R2的关系式如下:
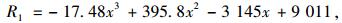
|
(5) |
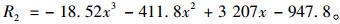
|
(6) |
需要注意的是,联合函数(5)和(6)求解,算出x≈2.056 m,因此得到:R1≈4 066.1,R2≈4 066.0。故在约2.06 m处,R1和R2相等,并且RA减小到最小,R1与R2之和达到最大。可以看出,2.06 m对于客家大桥桥梁结构支反力状态而言,是体系转换过程中的临界距离。对于整个体系转换过程,此时R1与R2基本相同,拆除支座1对结构的会产生一定的不利影响,在实际施工中应尽量避免。
随着距离的增加,R2逐渐增加,斜率减小,最终趋于稳定,支座2在结构中的参与度也逐渐增高;而R1逐渐减小,在体系转换过程中对结构受力的参与度逐渐减小,解除支座1对结构的影响也就越小。从这一点出发,距离越大对结构越有利,且1与2构成的新的临时支座体系的抗扭转刚度逐渐增大,这对于比较灵活的结构体系来说,更有利于结构在施工过程中的稳定。而考虑到实际施工的影响,d并不一定能取得最大值,故综合考虑各种因素,选择合适的距离,能兼顾施工场地、经济等的限制和优化体系转换过程中结构的受力。
对于状态3时结构支反力,由于结构形式已经确定,仅剩下支座A与永久支座2承担结构所有荷载,其反力大小由结构本身重量及跨径等因素决定,与d无关,故不再对其进行分析。
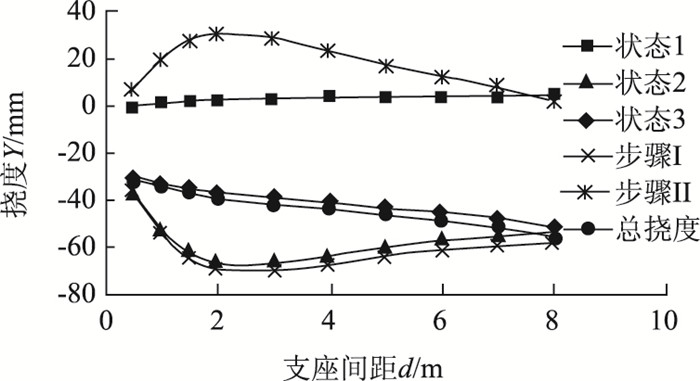
3.2.2 悬臂端挠度分析体系转换各个阶段悬臂端挠度数据记录见表 8,绘制图形见图 8,观察其变化趋势,并拟合出相关曲线函数。
| 距离 | 状态1 | 状态2 | 状态3 | 步骤Ⅰ | 步骤Ⅱ | 总挠度 |
| 0.5 | -0.5 | -37.5 | -30.3 | -37.0 | 7.2 | -29.9 |
| 1 | 1.2 | -52.5 | -32.9 | -53.7 | 19.5 | -34.2 |
| 1.5 | 1.7 | -61.9 | -35.1 | -64.8 | 26.9 | -36.8 |
| 2 | 2.4 | -66.4 | -36.7 | -68.7 | 29.7 | -39.0 |
| 3 | 2.8 | -66.9 | -38.8 | -69.7 | 28.1 | -41.6 |
| 4 | 3.2 | -63.8 | -41.2 | -66.9 | 22.6 | -44.3 |
| 5 | 3.4 | -60.1 | -43.2 | -63.5 | 16.9 | -46.6 |
| 6 | 3.7 | -57.1 | -44.9 | -60.7 | 12.2 | -48.6 |
| 7 | 3.9 | -55.1 | -47.6 | -59.0 | 7.4 | -51.5 |
| 8 | 4.2 | -53.4 | -51.5 | -57.6 | 1.9 | -55.6 |
|
| 图 8 悬臂端挠度变化趋势图 Fig. 8 Curves of deflection of cantilever end |
| |
由步骤Ⅰ挠度值拟合函数为:
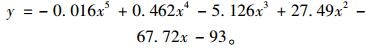
|
(7) |
由步骤Ⅱ挠度值拟合函数为:
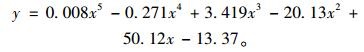
|
(8) |
由总挠度值拟合函数为:
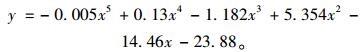
|
(9) |
从表 8及图 8中可以看出,随着d的增大,悬臂端经步骤Ⅰ后的下挠值及步骤Ⅱ的上挠值均呈现先增大后减小的趋势,总挠度则始终逐渐增大。通过对上述前两个函数计算,可得出这两段曲线的极值均在x=2~3 m附近,这表明在此区间内体系转换过程中悬臂端挠度变化最剧烈。因此应尽量避开。而客家大桥施工所选择的1.5 m距离虽然不是极大值点,但也处于相对不利的状态下,故而1.5 m虽能满足施工要求,但从本研究角度来说,并不是最好的选择。根据现场施工条件以及承台尺寸等信息,可采取上文中第2种形式的固结体系,距离可定在5~6 m的位置。
通过以上对支座反力和悬臂端挠度的分析可知,若要准确控制结构体系转换时悬臂端的挠度,顺利合龙,保证结构线形良好,则需选择合理临时固结方式,并建立有限元模型,进行计算分析,合理确定桥梁的施工预拱度。
4 结论与建议 4.1 结论(1) 体系转换过程中的悬臂端挠度由3部分组成,分别为墩梁固结转为铰接的转角位移带来的挠度、支点移动造成悬臂长度增大或减小带来的挠度、永久支座弹性压缩带来的挠度。
(2) 因边跨合龙段的预应力上拱作用,临时支座与永久支座距离越小,支点越趋近于悬臂端的临时支座3,R3越大;随着距离增加,支点与永久支座的距离逐渐减小,R1-R3也逐渐减小,当距离增到一定程度,反力差趋于稳定。
(3) 解除支座3之后,支座1与永久支座构成新的临时支座体系,二者距离越小,永久支座弹性压缩越小,反力也就越小,支点越偏向支座1,其受力越大;随着d的增加,C点挠度越大,永久支座的反力逐渐增加,支座1的反力逐渐减小;当两者反力值相等时的d为结构施工最不利距离;距离继续增加,支点逐渐偏向于永久支座,永久支座反力大于支座1的反力,且最终趋于完全体系转换之后的荷载值。
(4) 对于客家大桥来说,临时支座与永久支座的距离选择5~6 m的范围,更便于对结构线形的监控,更有利于桥梁悬臂施工过程中的结构稳定。
4.2 建议本研究根据客家大桥工程实际建立模型,旨在分析体系转换过程悬臂端挠度产生变化的原因,并得出以上结论。然而,由于对模型的简化处理,在分析中并未将温度、预应力、结构刚度等因素考虑在内,因此,对于处于体系转换状态下的结构体系来说,为更好地控制施工质量,故建议[15-18]:
(1) 选用刚度较大的临时固结方式。
(2) 为减小截面温差对结构变形及应力的影响,合龙宜在夜间进行。
(3) 为减小体系转换到合龙这段时间内的徐变及温度变化对结构产生的影响,应尽可能缩短工期。
(4) 解除临时固结后的结构相对灵敏,受外界因素影响效果明显,建议解除后尽快完成合龙段施工,避免因久置造成悬臂端挠度变化过大使合龙困难。
| [1] |
张继尧, 王昌将. 悬臂浇筑预应力混凝土连续梁桥[M]. 北京: 人民交通出版社, 2004. ZHANG Ji-yao, WANG Chang-jiang. Cantilever Casting Prestressed Concrete Continuous Beam Bridge[M]. Beijing: China Communications Press, 2004. |
| [2] |
邹立华. 一座多跨预应力混凝土连续梁桥的施工过程分析[J]. 公路交通科技, 2004, 21(1): 74-76. ZOU Li-hua. Simulation Analysis for Staged Construction of a Multi-span Prestressed Continuous Bridge[J]. Journal of Highway and Transportation Research and Developmen, 2004, 21(1): 74-76. |
| [3] |
张文学, 黄荐, 刘海陆. 预应力混凝土连续箱梁悬臂施工临时固结结构设计[J]. 公路交通科技, 2013, 30(2): 55-58. ZHANG Wen-xue, HUANG Jian, LIU Hai-lu. Design of Temporary Fixing Structure for Construction of Prestressed Concrete Continuous Box Girder Bridge Cantilever[J]. Journal of Highway and Transportation Research and Development, 2013, 30(2): 55-58. |
| [4] |
吴志和, 宁贵霞, 邓增轩. 悬臂施工临时固结简化模式及桥墩刚度对主梁变形的影响分析[J]. 兰州工业学院学报, 2014, 21(5): 40-45. WU Zhi-he, NING Gui-xia, DENG Zeng-xuan. The Analysis of the Main Beam's Deformation by the Temporary Simplified Consolidation Model for the Cantilever Construction and the Pier's Stiffness[J]. Journal of Lanzhou Institute of Technology, 2014, 21(5): 40-45. |
| [5] |
林晓威. 合龙方案和体系转换顺序对连续刚构桥结构状态的影响分析[J]. 福建建筑, 2014(4): 66-68. LIN Xiao-wei. Influence of Closing Plan and System Transformation Sequence on the Structural Condition of Continuous Rigid Frame Bridge[J]. Fujian Architecture & Construction, 2014(4): 66-68. |
| [6] |
曾振华, 习安, 李昭廷. 钢构-连续组合梁桥临时固结拆除顺序的研究[J]. 公路工程, 2012, 37(2): 37-40. ZENG Zhen-hua, XI An, LI Zhao-ting. The Removal Order Research for Structure-temporary Consolidation of the Rigid Frame-continuous Girders[J]. Highway Engineering, 2012, 37(2): 37-40. |
| [7] |
陈荣刚. 六跨连续刚构组合梁桥合拢方案研究[J]. 公路交通科技, 2014, 31(7): 91-96. CHEN Rong-gang. Study on Closure Scheme of Six-span Continuous Rigid Frame Composite Girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 31(7): 91-96. |
| [8] |
陈金水. 不同体系转换方案下连续梁桥成桥分析[J]. 安徽建筑, 2012(5): 134-135. CHEN Jin-shui. The Completion Analysis of Continuous Girder Bridge under Different System Transportation[J]. Fujian Architecture & Construction, 2012(5): 134-135. |
| [9] |
包仪军, 丁明波, 朱龙. 合龙方案对多跨连续梁桥施工监控的影响分析[J]. 铁道标准设计, 2016, 60(3): 82-86. BAO Yi-jun, DING Ming-bo, ZHU Long. Research on the Effect of Closure Program on Construction Monitoring of Multi-span Continuous Beam Bridge[J]. Railway Standard Design, 2016, 60(3): 82-86. |
| [10] |
陈宇, 贾艳敏. 预应力混凝土T梁在施工阶段的挠度和边界条件分析[J]. 公路交通科技, 2014, 31(11): 78-84. CHEN Yu, JIA Yan-min. Analysis on Deflection and Boundary Conditions of PC T-beam in Construction Phase[J]. Journal of Highway and Transportation Research and Development, 2014, 31(11): 78-84. |
| [11] |
王铭, 高艳梅, 周志祥, 等. 钢桁-砼组合连续刚构桥墩梁固结构造及分析[J]. 公路工程, 2015, 40(4): 67-73. WANG Ming, GAO Yan-mei, ZHOU Zhi-xiang, et al. The Construction Analysis of the Pier-girder-connection of Steel Truss-concrete Composite Continuously Ridged Bridge[J]. Highway Engineering, 2015, 40(4): 67-73. |
| [12] |
范立础. 预应力混凝土连续梁桥[M]. 北京: 人民交通出版社, 2001. FAN Li-chu. Prestressed Concrete Continuous Beam Bridge[M]. Beijing: China Communications Press, 2001. |
| [13] |
黄绳武. 桥梁施工及组织管理[M]. 北京: 人民交通出版社, 1992. HUANG Sheng-wu. Bridge Construction and Organization Management[M]. Beijing: China Communications Press, 1992. |
| [14] |
魏胜勇, 王根会. 结构体系转换对PC连续梁桥变形的影响研究[J]. 兰州交通大学学报, 2004, 23(1): 34-37. WEI Sheng-yong, WANG Gen-hui. Study on Influence of System Conversion of Construction to Deformation of PC Continuous Beam Bridge[J]. Journal of Lanzhou Jiaotong University:Natural Science Edition, 2004, 23(1): 34-37. |
| [15] |
顾颖, 李亚东, 姚昌荣. 太阳辐射下混凝土箱梁温度场研究[J]. 公路交通科技, 2016, 33(2): 78-84. GU Ying, LI Ya-dong, YAO Chang-rong. Research of Temperature Field of Concrete Box Girder under Solar Radiation[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2): 78-84. |
| [16] |
王毅, 叶见曙. 混凝土箱梁悬臂施工中温度梯度对标高影响的分析与控制[J]. 公路交通科技, 2009, 26(8): 89-93. WANG Yi, YE Jian-shu. Analysis and Control of Temperature-gradient's Influence on Formwork Erection Elevation during Balanced Cantilever Cast-in-place Segmental Construction of Concrete Girder[J]. Journal of Highway and Transportation Research and Development, 2009, 26(8): 89-93. |
| [17] |
叶见曙, 雷笑, 王毅. 基于统计分析的混凝土箱梁温差标准值研究[J]. 公路交通科技, 2009, 26(11): 50-54. YE Jian-shu, LEI Xiao, WANG Yi. Study of Characteristic Value of Thermal Difference of Concrete Box Girder Based on Statistical Analysis[J]. Journal of Highway and Transportation Research and Development, 2009, 26(11): 50-54. |
| [18] |
宋郁民, 刘媛, 周世军. 预应力混凝土桥梁悬臂施工中徐变挠度的计算[J]. 兰州交通大学学报, 2008, 27(4): 25-28. SONG Yu-min, LIU Yuan, ZHOU Shi-jun. Calculation of Creep Deflection in Cantilevered Construction of Long Span Prestressed Concrete Bridge[J]. Journal of Lanzhou Jiaotong University, 2008, 27(4): 25-28. |
 2017, Vol. 34
2017, Vol. 34
