扩展功能
文章信息
- 徐佰顺, 钱永久, 唐继舜, 马明, 李晓斌
- XU Bai-shun, QIAN Yong-jiu, TANG Ji-shun, MA Ming, LI Xiao-bin
- 基于黏弹性本构的CFRP-钢界面应力参数敏感性分析
- Analysis on CFRP-to-steel Interfacial Stress Parameter Sensitivity Based on Viscoelastic Constitution
- 公路交通科技, 2017, 34(11): 57-63
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(11): 57-63
- 10.3969/j.issn.1002-0268.2017.11.009
-
文章历史
- 收稿日期: 2016-10-26
2. 西南交通大学 土木工程学院, 四川 成都 610031
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu Sichuan 610031, China
近年来,粘贴碳纤维增强复合材料(CFRP)加固钢结构技术作为一种高效率、低成本的钢结构修复方法,已在土木工程领域得到了广泛的研究和应用。其应用领域包括钢结构承载能力加固、疲劳加固、腐蚀加固和脆性加固等。目前粘贴CFRP加固混凝土结构技术的研究和应用比较成熟[1-2],但CFRP加固钢结构技术研究还不够系统和完善。
粘贴CFRP加固钢结构后,黏结界面对荷载的传递起着重要的作用。因此分析黏结界面的应力状态对于了解荷载的传递机理和界面的破坏模式是非常重要的。彭福明[3]推导了FRP加固钢板和FRP加固钢梁的界面应力计算公式;邓军和黄培彦[4]对CFRP板加固钢梁界面应力进行了理论分析和试验研究;Narayanamurthy等[5]推导了任意荷载作用时粘贴加固钢梁界面应力的计算公式,并考虑了剪切变形的影响。
环氧树脂胶粘剂作为CFRP加固钢结构时常用的粘结剂,常温下就表现出一定的黏弹性行为。Hamed和Chang[6]及Mancusi等[7]通过长期加载试验表明胶粘剂的黏弹性会导致加固梁界面应力发生重分布,且加载应力越大应力重分布现象越明显。为获得胶粘剂的黏弹性本构关系,研究者们开展大量的试验研究,包括胶体的单轴拉伸蠕变试验[8-10]和CFRP-混凝土双剪试件的蠕变试验[11-12]。通过对试验数据的回归分析,建立的黏弹性本构模型有广义的Maxwell模型[12]、改进的Maxwell模型[11]、Burger模型[8]以及改进的Burger模型[9-10]。基于这些本构模型,可以采用有限元方法研究黏结界面的应力分布。Houhou等[8]将Burger模型应用于CFRP-混凝土双剪试件界面应力的计算中,得到的分析结果与试验数据吻合较好。
鉴于目前CFRP-钢界面应力分析中未考虑胶粘剂黏弹性性质的影响。本研究以胶粘剂黏弹性本构关系为计算基础,利用有限元软件ABAQUS对典型的粘贴CFRP加固简支钢梁进行了计算分析,研究界面应力随加载时间的变化规律,详细地讨论CFRP弹性模量变化、CFRP厚度变化、胶层厚度变化和CFRP端部到支座的距离变化对CFRP-钢界面应力的影响。
1 黏弹性分析的有限元法黏弹性材料综合地体现弹性固体和黏性流体的双重特性[13],其随时间而变化的变形过程,主要表现为蠕变(应力不变时应变随时间增长)和应力松弛(应变不变时应力随时间衰减)。环氧树脂胶粘剂作为高分子材料,即使玻璃转变温度高于常温,仍表现出一定的黏弹性行为。胶粘剂的黏弹性行为与环境温湿度、负荷时间、加载速率和应变幅值等有密切关系。
胶层材料的蠕变应变率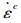
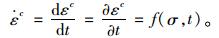
|
(1) |
对于多维应力状态的蠕变问题,应以等效蠕变应变率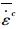
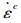
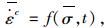
|
(2) |
可建立Mises型蠕变增量本构关系[14]:
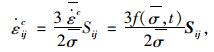
|
(3) |
式中,
按蠕变本构理论建立时间步长Δti的表达式:
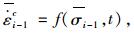
|
(4) |
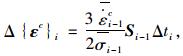
|
(5) |
式中,εc为蠕变应变分量列阵,S为应力偏量列阵。
按欧拉方法建立:
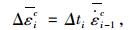
|
(6) |
由本构方程求Δ{εc}i。
因蠕变引起的等效节点力Δ{R}ic为[15]:
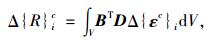
|
(7) |
式中,B为应变矩阵,D为弹性矩阵。
可得到如下平衡方程,即:
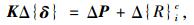
|
(8) |
式中,K为总刚度矩阵;δ为整体结构的节点位移列阵;P为整体结构的节点荷载列阵。
由式(8)解得位移增量Δδ,再求应变增量、应力增量,得到该时间步末的应变、应力等。在求出初始线弹性解后,便可由式(4)至式(8)求出各时间步末的位移、应变和应力。
2 有限元模型的建立 2.1 胶粘剂黏弹性本构关系空间应力状态下,以微分算子形式表示的黏弹性材料本构关系为:
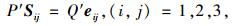
|
(9) |
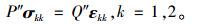
|
(10) |
式中,P′,Q′,P″和Q″为对时间t的微分算子;Sij和eij分别为偏应力张量和偏应变张量;σkk和εkk分别为球形应力张量和球形应变张量。
对于胶粘剂这种黏弹性材料来说,其体积变形是弹性的,其流变性质主要表现在剪切变形方面,因而式(10)中P″=1,Q″=3K(K为体积弹性模量)。
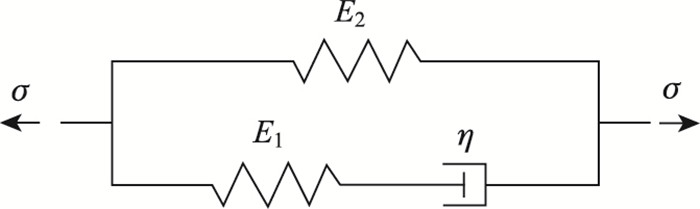
本研究采用Meshgin等[11]建立的改进的Maxwell模型来表征胶层的黏弹性性质,如图 1所示。该模型是由Maxwell模型和弹簧元件并联而成,参数E1和η分别代表Maxwell模型中弹性模量和黏度系数,E2代表弹簧元件的弹性模量。一般情况下,这些参数与环境温度、湿度和加载条件有关。为便于研究,本文假定这些参数为常数。该本构模型的微分算子可表示为:
|
| 图 1 改进的Maxwell模型 Fig. 1 Modified Maxwell model |
| |
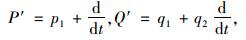
|
(11) |
式中,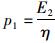
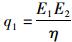
假设图 1中本构模型两端施加的荷载为剪应力τ:

|
(12) |
式中,τ0为初始剪应力,H(t)为单位阶跃函数。
借鉴文献[16]中FRP加固钢筋混凝土梁界面应力重分布研究的思路,结合式(9)和式(11),有:
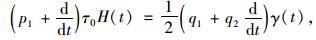
|
(13) |
式中γ(t)为胶层剪应变。
式(13)两边取Laplace变换,整理得:
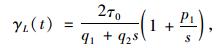
|
(14) |
式中,γL(t)为Laplace象空间内胶层的剪应变。
式(14)两边取Laplace逆变换后,有:
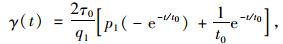
|
(15) |
式中,t0为退化时间,t0=q2/q1。
定义初始剪切模量μ0和极限剪切模量μ∞为:
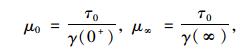
|
(16) |
在式(15)中取t=0和t=∞,有:
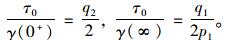
|
(17) |
结合式(15)有:q2=2μ0,E1=2μ∞,以及E2=2(μ0-μ∞)。
已知弹性模量E和泊松比ν的情况下,可以根据μ=E/2(1+ν)计算初始剪切模量μ0。假定极限剪切模量和退化时间分别为:
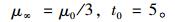
|
(18) |
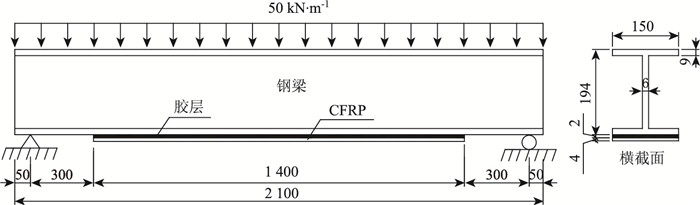
典型的粘贴CFRP加固简支钢梁如图 2所示。均布荷载为50 kN·m-1,钢梁长度为2 100 mm,梁高为194 mm,宽为150 mm,翼缘厚为9 mm,腹板厚为6 mm,粘贴CFRP长度为1 400 mm,宽度为150 mm,厚度为4 mm,胶层厚度为2 mm。材料力学性能参数见表 1所示。
|
| 图 2 CFRP加固简支钢梁(单位:mm) Fig. 2 CFRP strengthened simple-supported steel beam(unit: mm) |
| |
| 钢 | 胶粘剂 | CFRP | |
| 弹性模量/GPa | 210 | 12.7 | 230 |
| 泊松比 | 0.3 | 0.3 | 0.35 |
计算分析采用有限元软件ABAQUS实现。假定CFRP-钢界面粘结可靠无滑移,采用简化的接触关系模拟CFRP-钢界面。钢、胶粘剂和CFRP这3种材料均采用C3D8R实体单元。钢和CFRP采用线弹性应力-应变关系,胶粘剂的黏弹性本构关系通过用户材料子程序UMAT实现。为保证计算精度CFRP端部采用较密的有限元网格,胶层单元的最小网格尺寸为0.25 mm。根据对称性取半跨结构建模,如图 3所示。

|
| 图 3 有限元模型 Fig. 3 Finite element model |
| |
2.3 有限元计算结果的验证
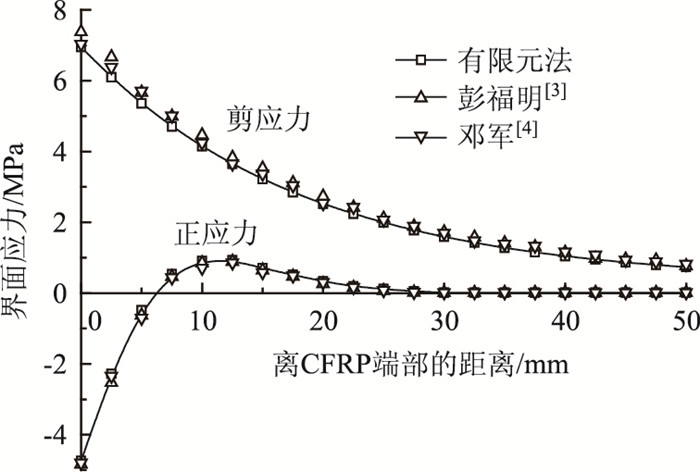
为确保有限元模型的正确性。当胶粘剂黏弹性本构模型中t=0时,提取界面应力的计算结果,将其与彭福明[2]和邓军[3]的理论公式计算结果进行比较,如图 4所示。从图 4中可见,最大界面剪应力和界面正应力均发生在CFRP端部,从CFRP端部向加固梁跨中方向,界面应力呈非线性分布,有限元模拟值与理论计算值基本一致。
|
| 图 4 界面应力有限元结果与理论结果比较 Fig. 4 Comparison of interfacial stresses between finite element result and theoretical result |
| |
图 5为CFRP加固简支钢梁界面剪应力和正应力随持载时间的变化情况。随着持载时间的增加,界面剪应力和正应力均发生应力重分布,界面峰值应力随时间增加而减小,应力集中现象得到缓解。随着持载时间的增加,胶层最大剪应力和最大正应力均会呈现减小趋势,30 d后CFRP端部界面剪应力和正应力分别减小了30.4%和40.3%。CFRP端部界面应力的减小能降低CFRP剥离的风险。

|
| 图 5 界面应力随持载时间的变化 Fig. 5 Interfacial stress varying with loading time |
| |
3 参数分析
为研究各参数变化对粘贴CFRP加固简支钢梁界面应力的影响,利用上节中建立的有限元分析模型,取CFRP端部界面剪应力和界面正应力为研究对象,同时考虑胶粘剂黏弹性引起的蠕变效应。某个参数变化时,其余参数不变。计算取4种时间工况如下:(a)t=0,(b)t=1 d,(c)t=10 d,(d)t=30 d。当胶层材料特性改变时,其黏弹性本构关系将发生变化,因此本文中不讨论胶层弹性模量变化对界面应力的影响。
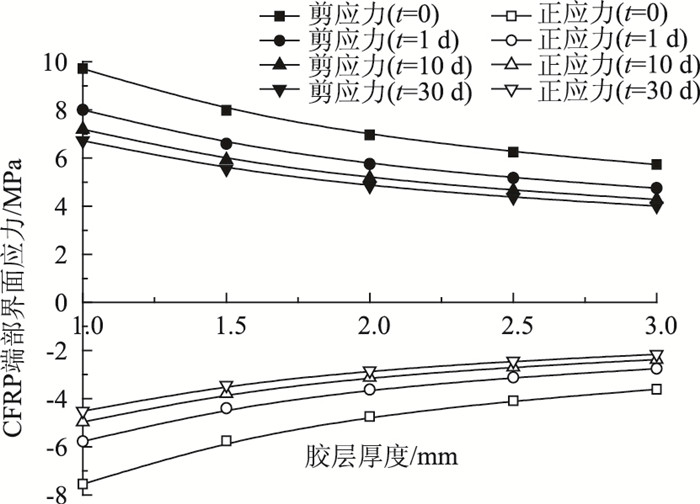
3.1 胶层厚度胶层厚度与CFRP端部界面应力的变化关系如图 6所示。从图 6可知,CFRP端部界面剪应力和正应力随胶层厚度的增加而减小,当t=0时,胶层厚度从1 mm变化为3 mm,CFRP端部界面剪应力和正应力分别减小了40.9%和52.2%,因此,进行钢梁加固设计时,在胶层厚度准许范围内宜采用较厚的胶层,以便减少界面应力,降低CFRP剥离的风险。当胶层厚度一定时,界面应力随时间的增加而减小,且开始减小较快,后期减小速率逐渐降低,这主要与胶粘剂的黏弹性本构关系有关。
|
| 图 6 CFRP端部界面应力与胶层厚度的关系 Fig. 6 Relation between interfacial stress in edge of CFRP and thickness of adhesive layer |
| |
3.2 CFRP厚度
CFRP厚度与CFRP端部界面应力的变化关系如图 7所示。由图 7可知,随着CFRP厚度的增加界面剪应力基本无变化,界面正应力成线性增加,当t=0时,CFRP厚度从1 mm增加到5 mm,界面正应力增加了近3.38倍,说明CFRP厚度对界面正应力影响很大。当CFRP厚度一定时,界面应力随时间增加而减小,CFRP厚度越大,胶粘剂黏弹性对界面正应力的影响越大。

|
| 图 7 CFRP端部界面应力与CFRP厚度的关系 Fig. 7 Relation between interfacial stress in edge of CFRP and thickness of CFRP |
| |
3.3 CFRP弹性模量
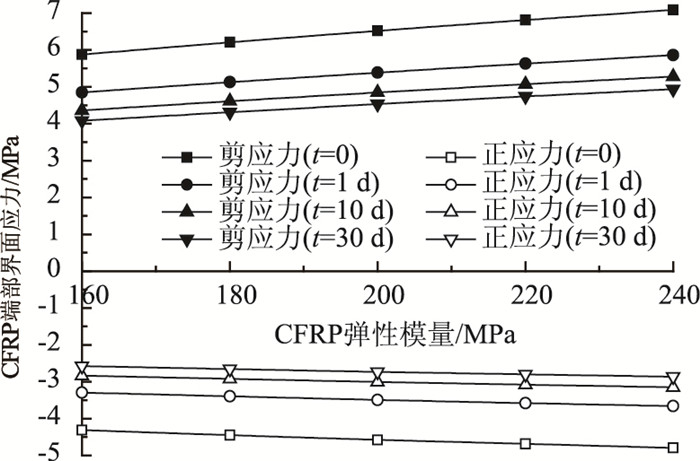
碳纤维材料包括板材和布材,根据《公路桥梁加固设计规范》(JTG/T J22-2008)[17]规定,Ⅱ级板材弹性模量应大于等于140 GPa。因此本研究选取CFRP弹性模量分别为160,180,200,220,240 GPa。CFRP弹性模量与CFRP端部界面应力的变化如图 8所示。由图 8可知,CFRP弹性模量越大,界面剪应力和正应力也越大,当t=0 d时,CFRP弹性模量从160 GPa增加到240 GPa,界面剪应力和正应力分布增加了20.7%和11.2%。当CFRP弹性模量一定时,界面应力随时间增加而减小。
|
| 图 8 CFRP端部界面应力与CFRP弹性模量的关系 Fig. 8 Relation between interfacial stress in edge of CFRP and elastic modulus of CFRP |
| |
3.4 CFRP端部离支座的距离
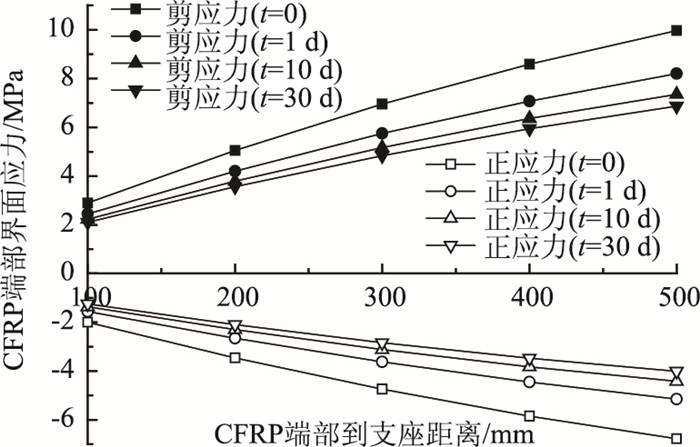
CFRP端部离支座的距离与CFRP端部界面应力的变化关系如图 9所示。由图 9可知,CFRP端部离支座越远,界面剪应力和正应力越大,当t=0时,CFRP端部离支座的距离由100 mm增加到500 mm,界面剪应力和正应力分别增加了2.44倍和2.39倍。究其原因是简支梁结构CFRP端部离支座越远,外荷载引起的CFRP端部弯矩越大,从而界面应力集中也越大。因此,为减小CFRP发生剥离破坏的风险,可适当使CFRP端部离支座近些,并在CFRP端部采用一定的锚固措施。当CFRP端部离支座的距离一定时,界面应力随时间的增加而减小。
|
| 图 9 CFRP端部界面应力与CFRP端部离支座距离的关系 Fig. 9 Relation between interfacial stress in edge of CFRP and distance from edge of CFRP to bearing |
| |
4 敏感性分析
运用敏感性分析的基本理论,从定量分析的角度研究各参数变动对加固梁界面应力的影响程度。设有一系统,系统特性F=f(x1, x2, …, xn)。在某一基准状态X′={x′1, x′2, …, xn′}下,系统特性为F′。分别令各参数在其各自可能的范围内变动,分析这些参数变动引起系统特性F偏离基准状态F′的趋势和程度。基准状态下的基准参数集可根据研究问题的具体情况给出。当分析参数xk对特性F的影响时,将其余参数取基准值且固定不变,此时系统特性F为[18]:
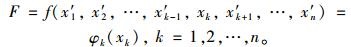
|
(18) |
通过式(18)仅能分析F对单参数的敏感性。而实际问题中大多需要研究多参数的敏感性。为此,定义无量纲化的敏感度函数和敏感度因子。敏感度函数Sk(xk)定义为:

|
(19) |
其中,k=1, 2, …, n。当|Δxk|/xk很小时,Sk(xk)可近似地表示为:
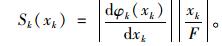
|
(20) |
在式(20)中取xk=x′k,即得到参数xk的敏感度因子S′k为:
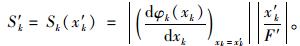
|
(21) |
S′k值越大,表明在基准状态下,F对xk越敏感。因此,当知道各参数的敏感度因子S′k后,通过比较S′k的大小,就可以实现界面应力对各参数的敏感性评价。
系统特性F用CFRP端部界面剪应力和界面正应力表征,敏感性分析的参数为:胶层厚度、CFRP厚度、CFRP弹性模量、CFRP端部离支座距离,各参数基准值分别为2.0 mm,4.0 mm,230 GPa,300 mm。
根据前述分析方法,对各参数进行分析,本研究以参数胶层厚度为例,说明敏感性分析的整个过程。图 6所示为界面应力随胶层厚度的变化曲线,当t=0时,观察曲线的形态进行回归分析,分别建立界面剪应力τ和界面正应力σ与胶层厚度d的函数关系:
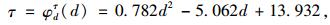
|
(22) |
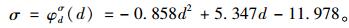
|
(23) |
根据式(19)计算出相应的敏感度函数:
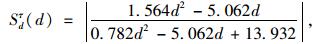
|
(24) |
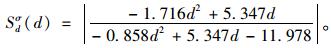
|
(25) |
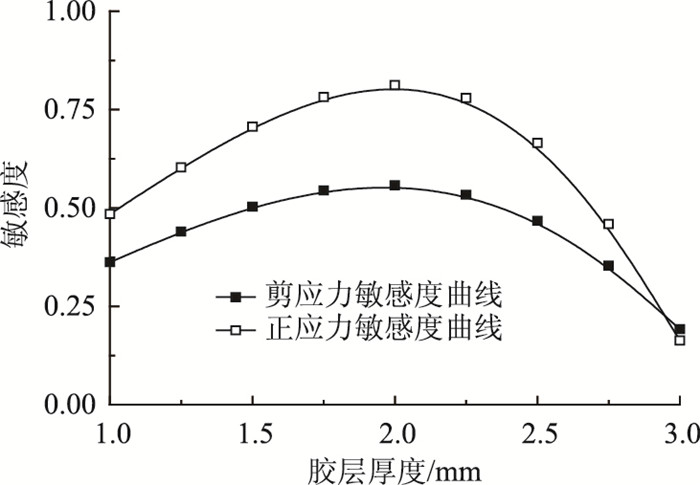
相应的敏感度曲线如图 10所示。从图 10中可知,界面剪应力和正应力的敏感度函数均为抛物线,当胶层厚度基准值为2 mm时,两条曲线均存在极大值,即相应的敏感度因子为Sdτ(d)=0.558和Sdσ(d)=0.812。
|
| 图 10 敏感度曲线 Fig. 10 Sensitivity curve |
| |
对于其他参数采用相同的分析思路,选取t=0 d时,图 7~图 9中相应曲线进行回归分析,即可得到界面剪应力和界面正应力与各参数的函数关系,根据式(19),计算出相应的敏感度函数。在式(21)中,取参数xk为基准参数x′k,即可得到相关敏感度因子S′k。各参数基准值的敏感度因子S′k,见表 2所示。
| 应力 | 敏感度因子 | |||
| S′胶层厚度 | S′CFRP厚度 | S′CFRP弹模 | S′CFRP端部离支座距离 | |
| 剪应力 | 0.558 | 0.002 | 0.515 | 1.359 |
| 正应力 | 0.812 | 0.956 | 0.351 | 0.747 |
由表 2可知,CFRP端部界面应力对不同参数的敏感度差别较大。对CFRP端部界面剪应力影响最大的参数为CFRP端部离支座距离,其敏感度因子为1.359;影响最小的参数为CFRP厚度,其敏感度因子为0.002。对CFRP端部界面正应力影响最大的参数为CFRP厚度,其敏感度因子为0.956;影响最小的参数为CFRP弹性模量,其敏感度因子为0.351。
5 结论借助有限元分析方法着重研究了胶粘剂黏弹性性质和各参数变化对CFRP-钢界面应力的影响,得到以下几点结论:
(1) 考虑胶粘剂的黏弹性后,界面应力发生应力重分布,界面峰值应力随时间增加而减小,应力集中现象得到缓解。30 d后CFRP端部界面剪应力和正应力分别减小了30.4%和40.3%。CFRP端部界面应力的减小能降低CFRP剥离的风险。
(2) 一般情况下,胶层越厚,CFRP越薄,CFRP弹性模量越小,CFRP端部离支座越近,CFRP-钢界面应力越小。
(3) 对CFRP端部界面剪应力影响最敏感的参数为CFRP端部离支座距离,其敏感度因子为1.359;对CFRP端部界面正应力影响最敏感的参数为CFRP厚度,其敏感度因子为0.956。
(4) 在进行粘贴CFRP加固简支钢梁加固设计时,应考虑胶层黏弹性性质对加固梁的长期影响。为避免加固梁过早的出现剥离破坏,可以适当增加胶层厚度和减小CFRP厚度,可适当使CFRP端部离支座近些,并在CFRP端部采用必要的锚固措施。
| [1] |
彭晖, 张建仁, 陈俊敏, 等. 表层嵌贴CFRP板条-混凝土界面黏结性能的试验研究[J]. 公路交通科技, 2014, 31(6): 70-79, 148. PENG Hui, ZHANG Jian-ren, CHEN Jun-min, et al. Experimental Study of Bond Performance of Interface between Near-surface-mounted CFRP Strips and Concrete[J]. Journal of Highway and Transportation Research and Development, 2014, 31(6): 70-79, 148. |
| [2] |
鲁乃唯, 刘扬, 彭晖. 预应力CFRP板加固混凝土梁桥的可靠度分析[J]. 公路交通科技, 2014, 31(12): 58-66. LU Nai-wei, LIU Yang, PENG Hui. Analysis on Reliability of RC Girder Bridge Strengthened with Pre-stressed CFRP Plates[J]. Journal of Highway and Transportation Research and Development, 2014, 31(12): 58-66. |
| [3] |
彭福明. 纤维增强复合材料加固修复金属结构界面性能研究[D]. 西安: 西安建筑科技大学, 2005. PENG Fu-ming. Research on Interfacial Performance of Metallic Structures Strengthened with Fibre Reinforced Polymers[D]. Xi'an:Xi'an University of Architecture and Technology, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10703-2006082574.htm |
| [4] |
邓军, 黄培彦. CFRP板加固钢梁界面应力的理论与试验研究[J]. 华南理工大学学报:自然科学版, 2007, 35(7): 10-14. DENG Jun, HUANG Pei-yan. Theoretical and Experimental Study on Interfacial Stresses of Steel Beam Strengthened with CFRP Plates[J]. Journal of South China University of Technology:Natural Science Edition, 2007, 35(7): 10-14. |
| [5] |
NARAYANAMURTHY V, CHEN J F, CAIRNS J. Improved Model for Interfacial Stresses Accounting for the Effect of Shear Deformation in Plated Beams[J]. International Journal of Adhesion & Adhesives, 2016, 64: 33-47. |
| [6] |
HAMED E, CHANG Z T. Effect of Creep on the Edge Debonding Failure of FRP Strengthened RC Beams:A Theoretical and Experimental Study[J]. Composites Science and Technology, 2013, 74: 186-193. |
| [7] |
MANCUSI G, SPADEA S, BERARDI V P. Experimental Analysis on the Time-dependent Bonding of FRP Laminates under Sustained Loads[J]. Composites Part B:Engineering, 2013, 46(2): 116-122. |
| [8] |
HOUHOU N, BENZARTI K, QUIERTANT M. Analysis of the Nonlinear Creep Behavior of Concrete/FRP-bonded Assemblies[J]. Journal of Adhesion Science and Technology, 2014, 28(14/15): 1345-1366. |
| [9] |
MAJDA P, SKTODZEWICZ J. A Modified Creep Model of Epoxy Adhesive at Ambient Temperature[J]. International Journal of Adhesion and Adhesives, 2009, 29(4): 396-404. |
| [10] |
COSTA I, BANOS J. Tensile Creep of a Structural Epoxy Adhesive:Experimental and Analytical Characterization[J]. International Journal of Adhesion and Adhesives, 2015, 59: 115-124. |
| [11] |
MESHGIN P, CHOI K, TAHA M. Experimental and Analytical Investigations of Creep of Epoxy Adhesive at the Concrete-FRP Interfaces[J]. International Journal of Adhesion and Adhesives, 2009, 29(1): 56-66. |
| [12] |
DIAB H, WU Z. A Linear Viscoelastic Model for Interfacial Long-term Behavior of FRP-concrete Interface[J]. Composites Part B:Engineering, 2008, 39(4): 722-730. |
| [13] |
冯师蓉, 胡霞光, 刘玉. 黏弹性材料的离散元数值分析[J]. 公路交通科技, 2008, 25(2): 12-15, 29. FENG Shi-rong, HU Xia-guang, LIU Yu. Numerical Analysis of Viscoelastic Materials Based on Discrete Element Method[J]. Journal of Highway and Transportation Research and Development, 2008, 25(2): 12-15, 29. |
| [14] |
穆霞英. 蠕变力学[M]. 西安: 西安交通大学出版社, 1990. MU Xia-ying. Creep Mechanics[M]. Xi'an: Xi'an Jiaotong University Press, 1990. |
| [15] |
王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003. WANG Xu-cheng. Finite Element Method[M]. Beijing: Tsinghua University Press, 2003. |
| [16] |
ZHANG C, WANG J L. Interface Stress Redistribution in FRP-strengthened Reinforced Concrete Beams Using a Three-parameter Viscoelastic Foundation Model[J]. Composites Part B:Engineering, 2012, 43(8): 3009-3019. |
| [17] |
JTG/T J22-2008, 公路桥梁加固设计规范[S]. JTG/T J22-2008, Specifications for Strengthening Design of Highway Bridges[S]. |
| [18] |
蒋树, 文宝萍. 基于不同方法的滑坡滑带力学参数敏感性分析[J]. 工程地质学报, 2015, 23(6): 1153-1159. JIANG Shu, WEN Bao-ping. Sensitivity Analysis of Mechanical Parameters of Landslide Slipzone Using Three Methods[J]. Journal of Engineering Geology, 2015, 23(6): 1153-1159. |
 2017, Vol. 34
2017, Vol. 34
