扩展功能
文章信息
- 孙聪, 余乐, 方四发, 郭鹏, 卢吉
- SUN Cong, YU Le, FANG Si-fa, GUO Peng, LU Ji
- 基于上限有限元法的节理岩质边坡稳定性分析
- Analysis on Stability of Jointed Rock Slope Based on Upper Bound FEM
- 公路交通科技, 2017, 34(11): 43-49
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(11): 43-49
- 10.3969/j.issn.1002-0268.2017.11.007
-
文章历史
- 收稿日期: 2016-02-16
2. 武汉市市政路桥有限公司, 湖北 武汉 430015;
3. 重庆交通大学, 重庆 400074
2. Wuhan Municipal Road and Bridge Co., Ltd., Wuhan Hubei 430015, China;
3. Chongqing Jiaotong University, Chongqing 400074, China
极限分析上限法是一种有效的边坡稳定性分析方法,它具有比极限平衡法更为严谨的理论基础,在得到安全系数的同时,可以给出极限状态的失稳速度场。目前国内外有许多学者致力于这方面的研究,Izbicki[1]曾提出了一种适用于求解边坡平移破坏的上限法,该法与传统的极限平衡法相似,将滑坡体划分为一系列垂直的条块,给定条块许可的位移场,利用功能平衡方程求解;Michalowski[2]也基于相似的理论提出了刚体条分上限法;陈祖煜等[3]以极限分析上限理论体系为基础,推出了基于斜条分法思想的斜条分上限解法;Sloan等学者[4-5]将土力学中的极限分析与有限元思想相结合,利用有限元中的插值思想解决了一系列困难,为极限分析在复杂条件下的工程应用打下了基础;殷建华和陈健等[6-7]采用刚体单元离散土体,提出考虑孔隙水压力条件下的刚体上限有限元分析法。高连生等[8]给予极限分析上限法推导出了带台阶的多级边坡稳定性分析方法。后面绝大部分学者[9-11]对极限分析法的研究均是沿着Sloan提出的思路开展的。
岩质边坡的稳定性分析是边坡工程中很重要的一环,由于岩体中含有大量断层、节理等不连续结构面,而且岩体的强度一般情况下是由这些结构面控制的,这给直接运用传统的边坡稳定性分析方法,如极限平衡法、有限元法和极限分析法求解制造了困难,必须对节理进行单独处理。赵尚毅等[12]利用无厚度接触单元对节理岩质边坡进行了分析;冯树荣等[13]推导了两组节理边坡的极限平衡解析解;李泽、王均星等[14]分别运用有厚度节理单元和无厚度节理单元来模拟岩体结构面,提出了基于非线性规划的岩质边坡有限元塑性极限分析下限法;陈炜等[15]将岩体离散为块体-结构面组成的块体系统,并假定块体为刚体,建立了基于非线性规划的极限分析下限模型。
其实,每组的节理面均表示在某一特定的方位上边坡的材料特性比较差,只需在处理这些特定方位时,采用相应的软弱节理面的材料特征即可。因此,基于该思想,对于任意应力点,从空间方位出发,建立基于方位离散线性化的极限分析上限法,该方法与传统的Sloan法有着异曲同工之妙,且可以很好地处理有多组节理面的岩质边坡。
1 上限法原理假定受力区域为Ω,Fi为体积力,Ti为边界A上的面力。对于任意运动许可的速度场vi*,上限法(又称机动法)认为基于内外虚功率平衡:
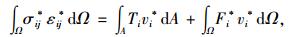
|
(1) |
所得到的力系Ti和Fi不小于真实的极限荷载。式中,εij*为对应于vi*的应变场; σij*为对应于εij*的并满足流动法则的应力场。因此,上限法要求在所有的速度场中,寻找使得所求力系最小的速度场。
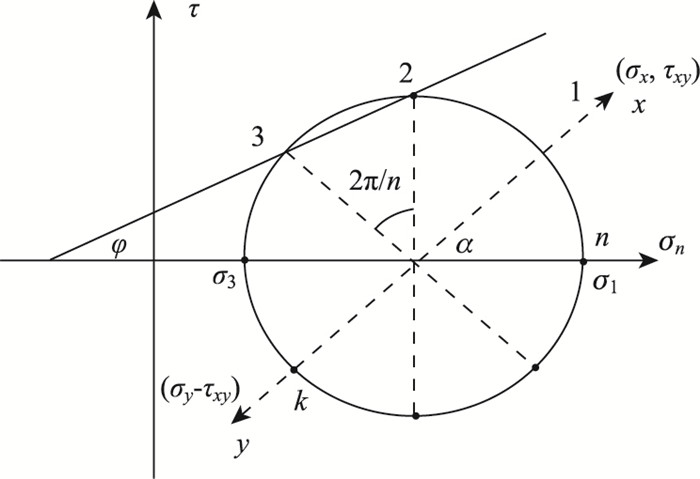
2 基于方位离散的塑性流动约束方程 2.1 基于方位离散的剪切屈服函数平面问题中的任意应力点对应的莫尔应力圆[16]如图 1所示,把该莫尔圆分成n等份,则相邻两离散点之间夹角为2π/n。
|
| 图 1 一个π范围的方位角被等分成n份 Fig. 1 A π degrees range of azimuth angle divided into n equal parts |
| |
需要注意的是,应力圆中的角度α其实只对应了现实中α/2的方位角[17],也即是说图 1中角度为2π的应力圆只对应了一个π角度范围内的方位角,另外一个π范围的方位角仍需进行n等分,这两部分的方位角合在一起总共被分成了2n份,且这两个范围的方位角等分离散点一一对应,对应点的σn相等,τ大小相等,符号相反。
将方位角以x轴为基准,则第k(k=1,2,…,2n)离散方位与x轴的夹角为:
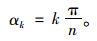
|
(2) |
对应到莫尔应力圆中相应的角度则是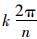
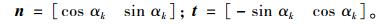
|
(3) |
设此点的应力张量为:
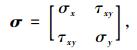
|
(4) |
则该方位平面上的正应力和剪应力分别为:
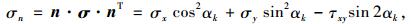
|
(5) |
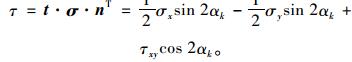
|
(6) |
该方位平面上的Mohr-Coulomb屈服准则为:
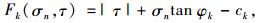
|
(7) |
式中,φk和ck为该方位平面上的摩擦角和黏聚力。将式(5)和(6)代入式(7),则形成了每个离散方位上的屈服条件。在全部方位的[0,2π]区间上,可以得到2n个线性化的屈服函数:
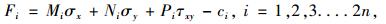
|
(8) |
式中,ci为第i个方位上的黏聚力。且当i=2k-1时(k=1,2,3,…,n),
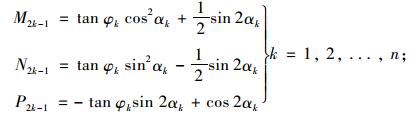
|
(9) |
当i=2k时,
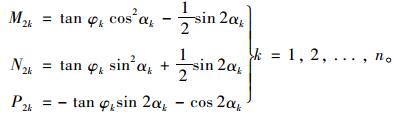
|
(10) |
至此,已经得到了线性化的基于方位离散的剪切屈服函数。在计算包含多组节理的岩质边坡时,只需将相应方位节理的抗剪强度参数(ci,φi)调成相应值即可。
2.2 塑性流动方程极限分析上限法要求计算区域内的速度场满足速度相容条件及塑性相关联流动法则,对于平面应变条件下的理想刚塑性体,将式(8)代入相关联流动法则可得到:
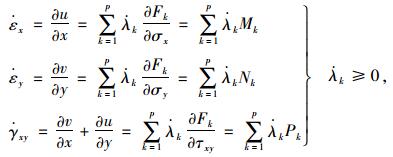
|
(11) |
式中,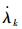
文中采用四边形网格来进行计算区域剖分,四边形网格与三角形网格最大的不同是形函数是非线性的,只需通过对单元建立积分意义上的协调方程的弱形式,来得到可以调整单元内部速度场的线性化的协调方程,具体过程见文献[18]。式(12)为四边形单元速度差值模式:
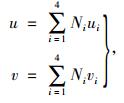
|
(12) |
式中,ui和vi分别为单元4个节点的水平和垂向速度;Ni为插值函数。
将式(12)代入式(11),并写成矩阵形式可得单元内部塑性流动约束方程:
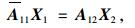
|
(13) |
式中,
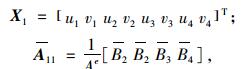
|
(14) |
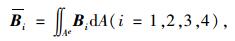
|
(15) |
Bi和Ae分别为应变矩阵和单元面积。
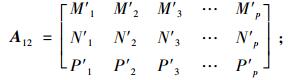
|
(16) |

|
(17) |
对摩尔库伦准则,当速度间断线上的塑性流动满足相关联流动法则时,则存在以下关系式:
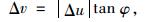
|
(18) |
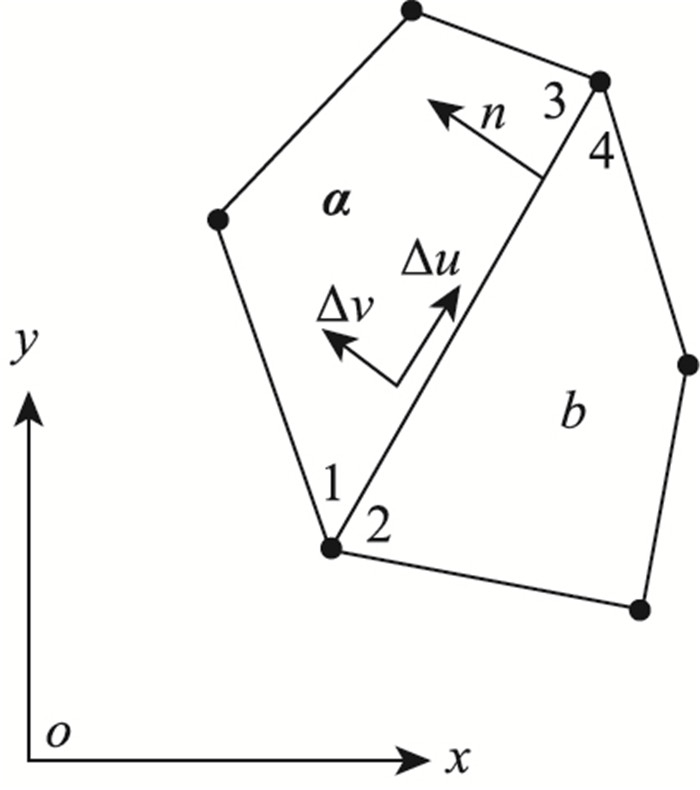
式中,Δv和Δu分别为速度间断线上任一点的法向和切向的相对速度,即相应的速度间断值,如图 2所示。
|
| 图 2 四边形单元速度间断线 Fig. 2 Velocity discontinuity line on quadrilateral element |
| |
按照文献[5]中的方法,对每对速度间断点引入一对非负变量u+和u-,令:
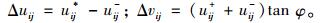
|
(19) |
因此,对于每条速度间断线,需要施加的塑性流动方程为:
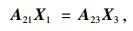
|
(20) |
式中,
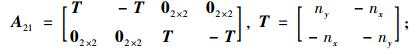
|
(21) |

|
(22) |
设n为一速度边界的法向量,nx和ny为其分量,已知该边界上的切向和法向速度分别为u和v,则该边界上的节点i的速度分量需满足:
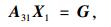
|
(23) |
式中,
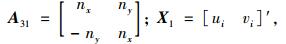
|
(24) |
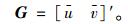
|
(25) |
(1) 单元内耗散功率
对于每个四边形单元,其内部相应的耗散能为:
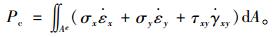
|
(26) |
将式(8)代入并写成矩阵形式为:
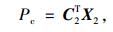
|
(27) |
其中,
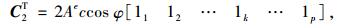
|
(28) |
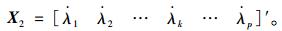
|
(29) |
(2) 间断线上功能耗散
在每条速度间断线上,由塑性剪切所产生的耗散能为:
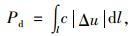
|
(30) |
式中l为间断线长度,令|Δu|=u++u-,代入式(29)并写成矩阵形式可得:
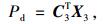
|
(31) |
其中,
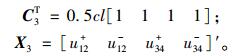
|
(32) |
(3) 外部功率
外部功率是指节点荷载(外荷载等效移植)在节点速度上做的功,写成矩阵形式为:
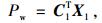
|
(33) |
式中,X1=[u1 v1 … um vm]′为节点速度向量;C1T=[px1 py1 … pxm pym]为节点荷载向量;m为节点总数。
4 上限法数学模型在得到了所有约束条件后,通过虚功方程即可形成最后的优化函数,优化变量为单元节点速度分量、速度间断线辅助变量以及单元塑性乘子。
参考文献[19],可以通过对强度参数进行调整,来使超载系数逼近于1,从而得到不易直接求解的强度折减系数。由于求解的只是破坏时结构的破坏形式,它仅与X1的相对大小有关,因此令:
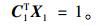
|
(34) |
此时,上限有限元法的数学模型为:
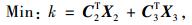
|
(35) |
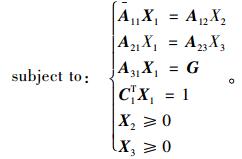
|
(36) |
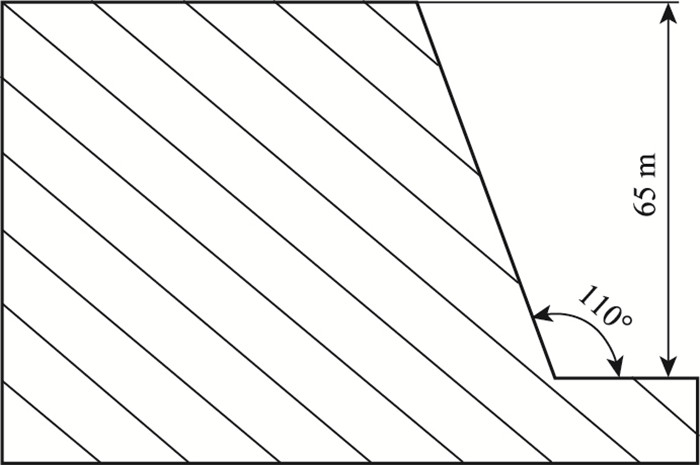
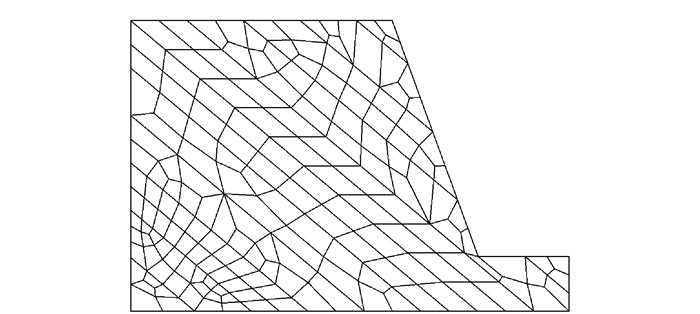
本算例取自文献[15],为具有一组间距为10 m软弱结构面岩质边坡,如图 3所示,软弱结构面贯通率100%,倾角为40°,边坡高度为65 m,岩体计算参数取值和网格划分如表 1和图 4所示。
|
| 图 3 算例1模型尺寸 Fig. 3 Model dimensions in calculation example 1 |
| |
| 材料 | γ/(kN·m-3) | c/(kN·m-2) | φ/(°) |
| 岩体 | 25 | 1 000 | 38 |
| 结构面 | — | 120 | 24 |
|
| 图 4 算例一网格划分 Fig. 4 Meshing of example 1 |
| |
各种方法计算的安全系数结果见表 2,其中刚体极限平衡法的结果是以结构面为单滑动面,逐条计算得到的。
文中采用16个方位离散点,40°方位采用软弱结构面强度参数,运用上限有限元法求出的安全系数为1.031,与表 2中的刚体下限法和Spencer法相比,误差分别为5.6%和3.7%,三者结果较为接近,说明了基于方位离散的上限有限元法在计算被结构面切割的岩质边坡稳定性时,也能取得较好的结果。
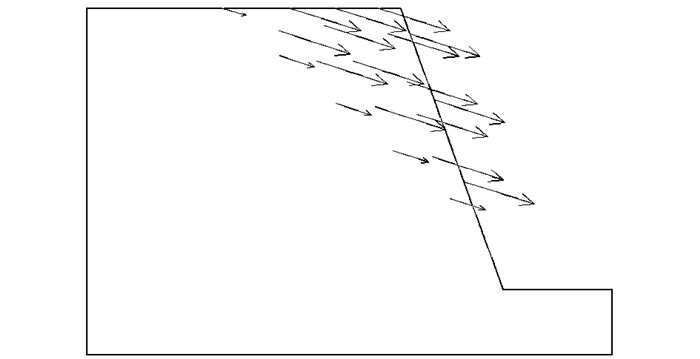
图 5为极限状态速度矢量图,可为后期边坡的支护做一定参考。
|
| 图 5 极限状态速度矢量图 Fig. 5 Vetorgram of velocity in critical state |
| |
5.2 算例2:有两组结构面的岩质边坡
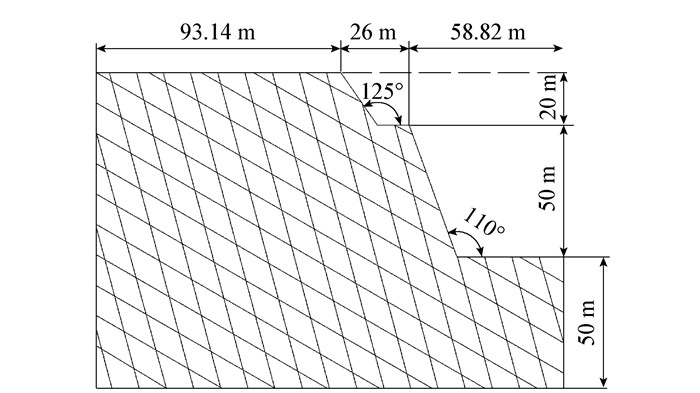
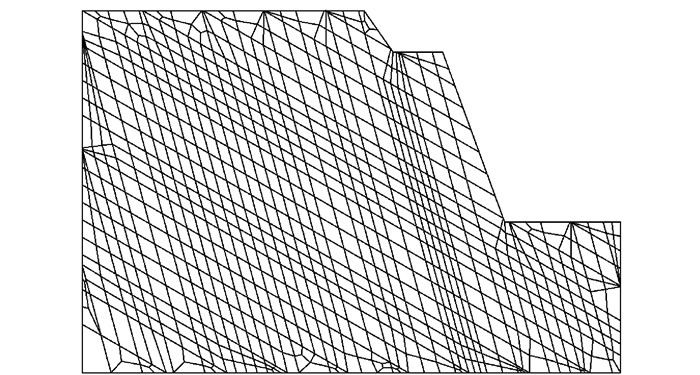
图 6为具有两组软弱结构面的岩质边坡[15]示意图,图中边坡的尺寸单位为m,每组结构面的间距均为10 m,贯通率100%,两组结构面倾角分别为30°和75°,岩体的计算参数取值和网格划分见表 3和图 7。
|
| 图 6 算例2模型尺寸 Fig. 6 Model dimensions in calculation example 2 |
| |
| 材料 | γ/(kN·m-3) | c/(kN·m-2) | φ/(°) |
| 岩体 | 25 | 1 000 | 38 |
| 30°结构面 | — | 120 | 24 |
| 75°结构面 | — | 120 | 24 |
|
| 图 7 算例2网格划分 Fig. 7 Meshing of example 2 |
| |
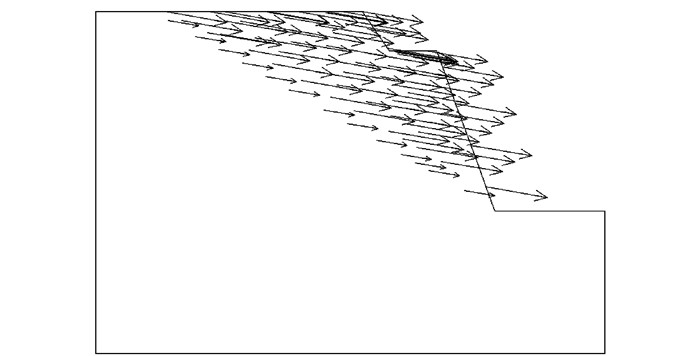
采用16个方位离散点数,30°和75°方位分别采用相应的软弱结构面强度参数,文中方法计算的结果为1.214,表 4为不同方法计算结果的对比。文中方法计算的安全系数略小于文献[15]基于极限分析下限法的结算结果,笔者认为这是由于文献[15]的下限法把每个三角形单元当作刚体处理,这就造成了一定的失真,且网格过于稀疏所致。相较而言,文中方法考虑了网格内的应力应变关系,结果更为合理。图 8为边坡极限状态速度矢量图。
|
| 图 8 边坡极限状态速度矢量图 Fig. 8 Vetorgram of velocity in critical state of slope |
| |
6 结论
岩质边坡由于含有多组结构面,运用传统的上限有限元法求解存在一定的困难。其实,每组的节理面均表示在某一特定的方位上边坡的材料特性比较差,只需在处理这些特定方位时,采用相应的软弱节理面的材料特征即可。因此,基于这一思想,对于任意应力点,从空间方位出发,建立了基于方位离散线性化的上限有限元法,该方法在考虑含多组节理面的岩质边坡上有着较好的优势和应用前景。两个算例证明了方法的有效性。
| [1] |
IZBICKI R J. Limit Plasticity Approach to Slope Stability Program[J]. Journal of Geotechnical & Geoenvironmental Engineering, 1981, 107(2): 228-233. |
| [2] |
MICHALOWSKI R L. Slope Stability Analysis:A Kinematical Approach[J]. Geotechnique, 1995, 45(2): 283-293. |
| [3] |
陈祖煜. 土力学经典问题的极限分析上、下限解[J]. 岩土工程学报, 2002, 24(1): 1-11. CHEN Zu-yu. Limit Analysis for the Classic Problems of Soil Mechanics[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(1): 1-11. |
| [4] |
LYAMIN A V, SLOAN S W. Upper Bound Limit Analysis Using Finite Element and Linear Programming[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2002, 26(2): 61-77. |
| [5] |
SLOAN S W, KLEEMAN P W. Upper Bound Limit Analysis Using Discontinuous Velocity Fields[J]. Computer Methods in Applied Mechanics and Engineering, 1995, 127(1): 293-314. |
| [6] |
殷建华, 陈健, 李焯芬. 岩土边坡稳定性的刚体有限元上限分析法[J]. 岩石力学与工程学报, 2004, 3(6): 898-905. YIN Jian-hua, CHEN Jian, LI Zhuo-fen. Upper Limit Analysis of Stability of Rock and Soil Slopes Using Rigid Finite Elements[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 3(6): 898-905. |
| [7] |
殷建华, 陈健, 李焯芬. 考虑孔隙水压力的土坡稳定性的刚体有限元上限分析[J]. 岩土工程学报, 2003, 25(3): 273-277. YIN Jian-hua, CHEN Jian, LI Zhuo-fen. A Rigid Finite Element Method for Upper Bound Limit Analysis of Soil Slopes Subjected to Pore Water Pressure[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(3): 273-277. |
| [8] |
高连生, 赵炼恒, 李亮, 等. 带台阶的多级边坡稳定性上限分析[J]. 公路交通科技, 2014, 31(6): 1-10. GAO Lian-sheng, ZHAO Lian-heng, LI Liang, et al. Analysis on Upper Bound of Stability of Multi-stage Slope with Benches[J]. Journal of Highway and Transportation Research and Development, 2014, 31(6): 1-10. |
| [9] |
王均星, 王汉辉, 张优秀, 等. 非均质土坡的有限元塑性极限分析[J]. 岩土力学, 2004, 25(3): 415-421. WANG Jun-xing, WANG Han-hui, ZHANG You-xiu, et al. Plastic Limit Analysis of Heterogeneous Soil Slope Using Finite Elements[J]. Rock and Soil Mechanics, 2004, 25(3): 415-421. |
| [10] |
黄阜, 杨小礼, 赵炼恒, 等. 基于Hoek-Brown破坏准则的浅埋条形锚板抗拔力上限分析[J]. 岩土力学, 2012, 33(1): 179-184, 190. HUANG Fu, YANG Xiao-li, ZHAO Lian-heng, et al. Upper Bound Solution of Ultimate Pullout Capacity of Strip Plate Anchor Based on Hoek-Brown Failure Criterion[J]. Rock and Soil Mechanics, 2012, 33(1): 179-184, 190. |
| [11] |
王根龙, 伍法权, 祁生文, 等. 加锚岩质边坡稳定性评价的极限分析上限法研究[J]. 岩石力学与工程学报, 2007, 26(12): 2556-2563. WANG Gen-long, WU Fa-quan, QI Sheng-wen, et al. Research on Limit Analysis Upper Bound Method for Stability Evaluation of Anchored Rock Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2556-2563. |
| [12] |
赵尚毅, 郑颖人, 邓卫东. 用有限元强度折减法进行节理岩质边坡稳定性分析[J]. 岩石力学与工程学报, 2003, 22(2): 254-260. ZHAO Shang-yi, ZHENG Ying-ren, DENG Wei-dong. Stability Analysis on Jointed Rock Slope by Strength Reduction FEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 254-260. |
| [13] |
冯树荣, 赵海斌, 蒋中明. 节理岩体边坡稳定性分析新方法[J]. 岩土力学, 2009, 30(6): 1639-1642. FENG Shu-rong, ZHAO Hai-bin, JIANG Zhong-ming. A New Method of Stability Analysis of Jointed Rock Slope[J]. Rock and Soil Mechanics, 2009, 30(6): 1639-1642. |
| [14] |
李泽, 王均星. 基于非线性规划的岩质变坡有限元塑性极限分析下限法研究[J]. 岩石力学与工程学报, 2007, 26(4): 747-753. LI Ze, WANG Jun-xing. Lower Bound Limit Study on Plastic Limit Analysis of Rock Slope Using Finite Elements Based on Nonlinear Programming[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 747-753. |
| [15] |
陈炜, 王均星. 节理岩质边坡的块体元塑性极限分析下限法[J]. 岩土工程学报, 2008, 30(2): 272-277. CHEN Wei, WANG Jun-xing. Plastic Lower Bound Limit Analysis Using Block Element Method for Jointed Rock Slope[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 272-277. |
| [16] |
孙聪, 李春光, 郑宏, 等. 同时考虑张拉及剪切破坏的边坡上限原理有限元法[J]. 岩石力学与工程学报, 2015, 34(增1): 2783-2791. SUN Cong, LI Chun-guang, ZHENG Hong, et al. Linearized Upper Bound Limit Analysis Considering Tension and Shear Failures for Slope Stability Problems[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 2783-2791. |
| [17] |
孙训方, 方孝淑, 关来泰. 材料力学(Ⅰ)[M]. 北京: 高等教育出版社, 2006. SUN Xun-fang, FANG Xiao-shu, GUAN Lai-tai. Mechanics of Materials(Ⅰ)[M]. Beijing: Higher Education Press, 2006. |
| [18] |
孙聪, 李春光, 郑宏, 等. 基于四边形网格的边坡上限有限元法[J]. 岩石力学与工程学报, 2015, 34(1): 114-120. SUN Cong, LI Chun-guang, ZHENG Hong, et al. Upper Bound Limit Analysis of Slopes Using Quadrilateral Finite Elements[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 114-120. |
| [19] |
李国英, 沈珠江. 下限原理有限单元法及其在土工问题中的应用[J]. 岩土工程学报, 1997, 19(5): 84-89. LI Guo-ying, SHEN Zhu-jiang. Lower Bound Finite Element Method and Its Application in Geotechnical Problems[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(5): 84-89. |
 2017, Vol. 34
2017, Vol. 34
