扩展功能
文章信息
- 朱洪洲, 范世平, 卢章天
- ZHU Hong-zhou, FAN Shi-ping, LU Zhang-tian
- 基于DSR时间扫描的沥青常应力疲劳演化规律分析
- Analysis on Fatigue Evolution Rule of Asphalt under Constant Stress Based on DSR Time Scanning
- 公路交通科技, 2017, 34(11): 8-14, 37
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(11): 8-14, 37
- 10.3969/j.issn.1002-0268.2017.11.002
-
文章历史
- 收稿日期: 2017-01-06
2. 重庆交通大学 土木工程学院, 重庆 400074;
3. 广西交通规划勘察设计研究院有限公司, 广西 南宁 530029
2. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China;
3. Guangxi Communication Planning Surveying & Design Institute Co., Ltd., Nanning Guangxi 530029, China
疲劳开裂是沥青路面主要损坏形式之一,是沥青路面结构设计和沥青混合料组成设计研究的重点。目前,国内外专家学者对沥青混合料疲劳性能做了大量研究[1-3]。且有研究表明沥青混合料疲劳裂缝最初产生于沥青胶浆内部或沥青与集料界面处[4-6],因此沥青的疲劳特性对沥青混合料的疲劳性能有重要影响,在研究沥青混凝土疲劳开裂之前很有必要对沥青疲劳性能进行研究。
过去受试验设备、试验方法等限制,针对沥青的疲劳寿命研究较少。直到20世纪末期,美国SHRP研究中形成了基于动态剪切试验的沥青疲劳性能检测分析方法,沥青的疲劳寿命才被重视并得以广泛研究。随着动态剪切流变仪(DSR)的发展,国内外学者采用动态剪切流变仪对沥青疲劳性能的研究日益兴起[7-11]。沥青的疲劳试验一般采用应力控制和应变控制两种模式进行室内试验和分析,两种控制模式下沥青疲劳性能具有显著差异。现有研究中,部分着眼于应力、应变控制模式下沥青疲劳性能差异的研究者,主要集中于疲劳评价指标[12-13]或疲劳模型的统一[14-16],缺乏对疲劳演化规律的分析。此外,多数研究者以同一种沥青的疲劳性能为研究对象[17-19],对同一控制模式下不同沥青的疲劳性能研究较少。
文中借助动态剪切流变仪,在应力控制模式下研究70#基质沥青和SBS改性沥青的疲劳性能差异,分析两种沥青的疲劳演化规律,确定沥青疲劳寿命,分析不同沥青的疲劳性能。研究成果可为沥青或沥青混合料疲劳指标的建立提供理论依据。
1 试验材料与方法 1.1 试验材料本研究选用中交70#道路石油沥青和SBS改性沥青,其技术指标如表 1所示。
| 试验项目 | 沥青种类 | 技术要求 | 试验结果 | 试验方法 |
| 针入度(100 g, 5 s, 25 ℃)/ 0.1 mm |
70# | 60~80 | 68 | T0604 |
| SBS | 40~60 | 57 | ||
| 软化点 (环球法)/℃ |
70# | ≥43 | 48.5 | T0606 |
| SBS | ≥60 | 67 | ||
| 延度(5 cm/min, 15 ℃)/cm | 70# | ≥40 | 75 | |
| 延度(5 cm/min, 5 ℃)/cm | SBS | ≥20 | 28 | T0605 |
| 弹性恢复(25 ℃)/% | SBS | ≥75 | 81 | T0662 |
| 离析 | SBS | ≤2.5 | 0.4 | T0661 |
| 运动黏度(135 ℃)/(Pa·s) | SBS | ≤3 | 2.3 | T0625 |
1.2 试验方法
采用动态剪切流变仪(DSR),在应力控制模式下进行时间扫描试验。试验温度30 ℃,加载频率10 Hz,平行板夹具直径8 mm,试验应力水平为0.05,0.10和0.15 MPa。
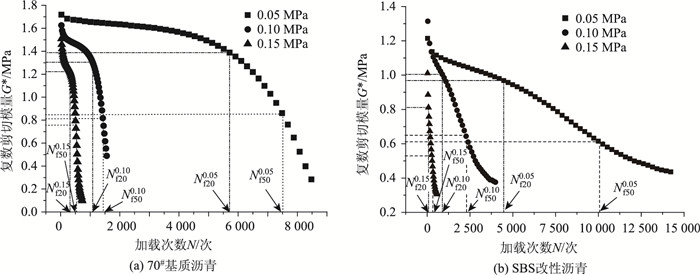
2 试验结果与分析 2.1 复数剪切模量变化规律沥青是典型的黏弹性材料,在其剪切变形过程中,用复数剪切模量(G*)来度量沥青材料抵抗剪切变形的总阻力,主要包括弹性和黏性两部分,弹性和黏性的相对指标可用相位角δ来表征。G*·cos δ为贮存剪切模量,表征沥青变形过程中能量的储存;G*·sin δ为损失剪切模量,表征沥青在剪切过程中内部摩擦产生的以热的形式散失的能量,其值越大,表示重复剪切试验能量损失越快,因此较小的G*·sin δ代表较好的抗疲劳能力。图 1表示70#基质沥青和SBS改性沥青复数剪切模量G*随荷载作用次数的变化规律(G*-N曲线)。
|
| 图 1 复数剪切模量随荷载作用次数变化规律 Fig. 1 Rules of complex shear modulus varying with loading times |
| |
由图 1所示,在同一应力水平下,随着荷载作用次数的增加,两种沥青复数剪切模量均有所下降,但二者下降趋势明显不同。70#基质沥青在下降过程中出现明显的转折点,复数剪切模量在转折点之前下降缓慢,说明该阶段沥青在重复剪切作用下抵抗剪切变形能力较好;但在转折点之后,复数剪切模量急剧下降直至沥青试样完全破坏,表示该阶段沥青发生疲劳破坏,抵抗剪切变形能力减小。将转折点定义为沥青疲劳破坏起始点,所对应的荷载作用次数记为Nf20。经计算,Nf20所对应的复数剪切模量值约为初始复数剪切模量的80%。当初始模量下降至50%时处于加速破坏阶段,以该点作为沥青疲劳破坏点,对应的荷载作用次数记为Nf50。从图中可看出在高应力水平下,Nf20和Nf50二者相差较小。文中以Nf50作为70#基质沥青疲劳寿命,记为NG*。
与70#基质沥青相比,SBS改性沥青由于改性剂的作用,疲劳破坏只有初始适应阶段和加速破坏阶段,但在加速破坏阶段复数剪切模量衰减速率逐渐减小,虽然也有类似于70#基质沥青的转折点,但转折点前后复数剪切模量变化趋势无显著差异。在荷载作用后期,SBS改性沥青复数剪切模量并不同于70#基质沥青的加速下降,而是趋于平稳直至试样破坏。导致这种现象产生的原因是改性剂增强了SBS改性沥青抵抗剪切变形的能力,在荷载作用过程中使沥青试样发生一定程度的自愈合,复数剪切模量下降缓慢。Nf50所对应的复数剪切模量靠近平缓区。
随着应力水平的提高,两种沥青的初始复数剪切模量都有所减小,且应力水平越高,复数剪切模量衰减速度越快,试件破坏前所能承受的加载次数以及复数剪切模量衰减至50%时对应的重复剪切次数越低,即应力越大,沥青疲劳寿命越低。
2.2 耗散能变化率变化规律 2.2.1 耗散能变化率沥青在重复剪切变形过程中,必然伴随着能量的耗散,这部分能量包含了弹性和黏性两部分损耗的能量,通过分析加载过程中耗散能的变化,避免考虑沥青黏弹性能带来的影响,可以完整地表示沥青的疲劳损伤变化过程。耗散能变化率就是指相邻加载次数的耗散能变化速率,也称损伤率(Damage Rate),如式(1)、(2)所示。
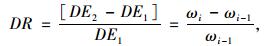
|
(1) |
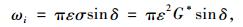
|
(2) |
式中,DR为耗散能变化率;wi为第i次荷载作用中耗散的能量;wi-1为第i-1次荷载作用中耗散的能量;G*为复数剪切模量;δ为相位角。
该模型用耗散能变化率来表征沥青疲劳损伤的变化规律,假设在荷载作用初期,沥青在每个荷载作用周期内基本没有发生损伤或损伤程度小到可以忽略,即每个荷载作用周期内能量基本保持恒定,第i次耗散的能量与i-1次耗散能量差接近于零,即DR接近零;随着荷载的连续作用,沥青发生疲劳损伤并不断发展,每个荷载作用周期内沥青损伤程度逐渐增大,即耗散能逐渐增大,导致DR值迅速增大,DR-荷载作用曲线中会出现明显的转折点,可将该转折点定义为沥青疲劳寿命破坏点,所对应的荷载作用次数定义为沥青疲劳寿命。
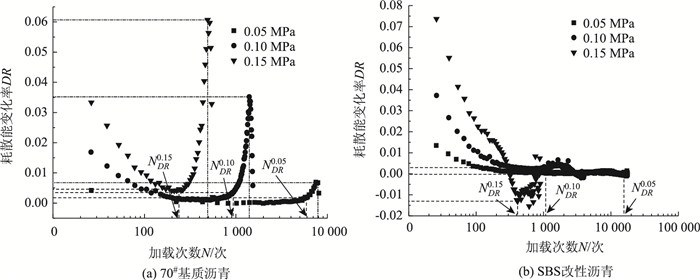
2.2.2 耗散能变化率演化规律图 2是70#基质沥青和SBS改性沥青在不同应力水平下的耗散能变化率随加载次数变化的曲线(DR-N曲线)。
|
| 图 2 耗散能变化率随荷载作用次数变化规律 Fig. 2 Rules of dissipative energy change rate varying with loading times |
| |
由图 2可见,在荷载作用初期,70#基质沥青的DR值逐渐下降至0,且下降速率与应力水平有关,应力越大,下降越快,这表明沥青在荷载作用下开始发生微损伤,且损伤发展程度随着应力的增大而增大。随着荷载作用次数的增加,DR值急剧增大并达到峰值,然后迅速下降,表明沥青疲劳损伤快速发展,导致沥青发生疲劳破坏。DR-N曲线中先后出现了两个转折点将70#基质沥青疲劳破坏过程分为3个阶段,第1个转折点之前表示沥青处于初始适应阶段,第2个转折点之后表示沥青已疲劳破坏,两个转折点之间表示沥青疲劳损伤发展阶段。两个转折点所对应的荷载作用次数差距较小,将第1个转折点对应的荷载作用次数定义为70#基质沥青疲劳寿命,用NDR表示。
对于SBS改性沥青,由于改性剂改善了沥青的黏弹性能,导致其耗散能变化率随荷载作用次数的变化并没有70#基质沥青显著,虽在DR-N曲线中隐约可以找到类似70#基质沥青的两个模糊转折点,但转折点前后的DR值变化并无显著差异。同70#基质沥青将第1个转折点所对应的荷载作用次数定义为SBS改性沥青的疲劳寿命。从图 2中可以看出,低应力状态下,耗散能变化率随着荷载作用次数的增加缓慢下降并趋于0,表明沥青在荷载作用过程中疲劳损伤缓慢发展。在高应力(0.15 MPa)状态下,DR值出现负值现象,表明随着荷载作用次数的增加,SBS改性沥青耗散能逐渐下降,究其原因,主要是由于在高应力状态下,SBS改性剂分子结构发生破坏,一部分能量因抵抗分子间的范德华力被消耗,导致耗散能下降。
对于同一沥青,随着应力水平的增加,DR-N曲线中转折点出现的时间明显提前,荷载作用次数降低,即应力越高,疲劳寿命越短。
2.3 累计耗散能比变化规律 2.3.1 累计耗散能比累计耗散能比是用能量表征沥青疲劳变化规律的另一指标,假定每个荷载作用周期内,材料的损伤都可以小到忽略不计,即每个荷载作用周期产生的耗散能wi是恒定的,可令wi=wn,累计耗散能和累计耗散能比见式(3)和式(4):
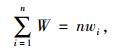
|
(3) |
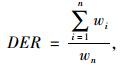
|
(4) |
式中,DER为累计耗散能比;wi为第i次荷载作用中耗散的能量;wn为第n次荷载作用中耗散的能量。结合式(3)和式(4)可看出,当材料损伤程度很小或者没有损伤时,累计耗散能比DER就等于加载次数N;当材料在N+1次产生损伤时,由于新的损伤消耗了能量,wN+1将不再保持恒定,DER与N的差值增大, 即可将DER-N曲线的转折点所对应的重复剪切次数作为沥青的疲劳寿命。
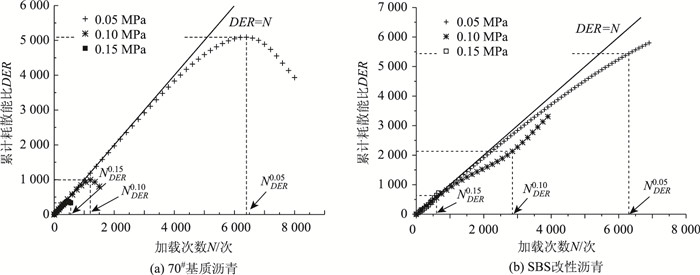
2.3.2 累计耗散能比演化规律70#基质沥青和SBS改性沥青累计耗散能比与荷载作用次数变化关系如图 3所示。
|
| 图 3 累计耗散能比随荷载作用次数变化规律 Fig. 3 ules of cumulative dissipative energy ratio varying with loading times |
| |
从图 3可见,70#基质沥青的DER-N曲线大致呈抛物线的形状,曲线中存在明显的转折点。在荷载作用初期,累计耗散能比与荷载作用次数的关系近似为斜率等于1的直线,这表明此时沥青内部产生的损伤很小,处于疲劳破坏的初始适应阶段;然后随着荷载作用次数增多,曲线逐渐偏离DER=N直线,损伤或者裂纹不断发展,消耗了更多的能量,沥青处于疲劳破坏的发展阶段;当加载次数达到一定程度后,DER的增长速度≤0,曲线出现转折点,将此转折点对应荷载作用次数定义为70#基质沥青的疲劳寿命,用NDER表示。转折点之后,DER值随荷载作用次数增加而显著降低,沥青进入完全破坏期。转折点所对应的DER值偏离目标直线约20%。
对于SBS改性沥青,在荷载作用初期的DER-N曲线与70#基质沥青一样近似斜率为1的直线,沥青内部没有损伤或损伤很小。随着荷载作用次数的增加,DER-N曲线虽然偏离直线DER=N,但DER的增长速率稍微降低后又恢复原状,甚至可能超过原来的增长速率,这主要是由于SBS改性剂分散在沥青中,使沥青弹性恢复能力大大提高,当SBS改性沥青受到损伤时,沥青发生一定程度自愈合。虽然SBS改性沥青DER-N曲线偏离DER=N直线,表明随着荷载次数的增加,沥青发生一定疲劳破坏,但由于DER-N曲线无明显变化点,为了便于对比,文中以DER-N曲线偏离目标直线20%时所对应的荷载作用次数作为SBS改性沥青疲劳寿命。
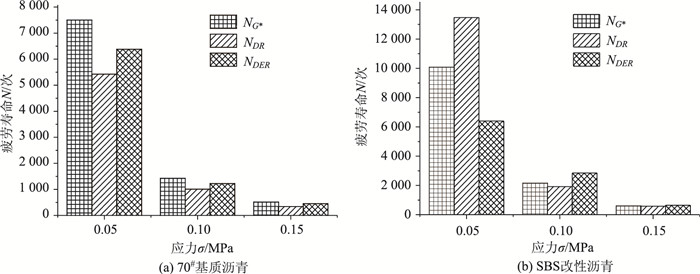
3 基于不同指标的疲劳性能评价 3.1 基于不同指标的疲劳寿命对比基于以上3种评价方法得到的疲劳寿命评价结果绘制成柱状图,如图 4所示。从图 4可以看出,对于70#基质沥青,同一应力状态下,不同指标确定的疲劳寿命大小依次是:NG*>NDER>NDR,相同条件下,疲劳寿命NG*比疲劳寿命NDR超出36%,比NDER超出18%。而SBS改性沥青在低应力状态下(0.05 MPa),NDR最大,超出NG*和NDER约40%和60%,主要是因为在低应力状态下,沥青试样变形较小,每个荷载周期内能量耗散相差不大,故耗散能变化率小,承受荷载作用次数多,即疲劳寿命大。随着应力水平增大,沥青疲劳损伤程度加大,在每个荷载作用周期内耗散能增多使沥青承受荷载作用次数降低,因此DR-N曲线确定的NDR值减小。
|
| 图 4 沥青基于不同评价方法的疲劳寿命对比图 Fig. 4 Comparison of fatigue lives of asphalt based on different evaluation methods |
| |
3.2 沥青常应力疲劳方程
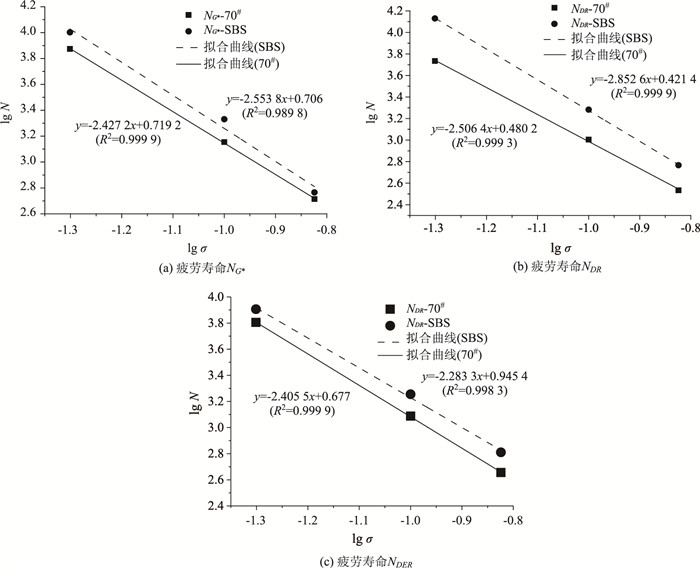
沥青DSR疲劳试验的疲劳寿命与加载应力服从幂指数关系[20-21],即N=Kσ-b,其中N为沥青疲劳寿命;σ为应力大小;K,b为回归系数,K与材料的剪切强度有关,b为沥青疲劳寿命的应力或应变敏感度。根据试验结果,70#基质沥青和SBS改性沥青相同指标确定的疲劳寿命与荷载作用次数双对数坐标关系及疲劳方程如图 5所示。从图 5可以看出,由于改性剂的作用,同一指标下SBS改性沥青疲劳寿命优于70#基质沥青疲劳寿命,且随着应力的增加,两种沥青疲劳寿命均下降。
|
| 图 5 沥青疲劳寿命与应力的双对数关系 Fig. 5 Double logarithm relations between fatigue life and stress |
| |
4 结论
(1) 沥青疲劳曲线变化规律受沥青种类影响较大,文中所采用的疲劳破坏分析方法中,70#基质沥青的疲劳曲线变化规律明显,曲线中有明确表示沥青发生疲劳破坏的突变点,而SBS改性沥青由于改性剂改变了沥青黏弹性能,在加载过程中,沥青弹性恢复能力加强,导致疲劳曲线不同于70#基质沥青呈现明显规律性。同时,SBS改性沥青疲劳寿命明显优于70#基质沥青。
(2) 在应力控制模式下,无论70#基质沥青还是SBS改性沥青,疲劳寿命都随着应力的增大而减小。
(3) 通过耗散能变化分析确定的沥青疲劳寿命物理意义明确,符合沥青疲劳破坏规律。而通过复数剪切模量变化规律确定的疲劳寿命经验性较强,缺乏一定理论支撑,且在高应力状态下,70#基质沥青G*-N曲线转折点对应的荷载次数接近50%初始模量对应的荷载次数。
(4) 本研究主要针对连续加载模式下沥青疲劳寿命进行分析,但并未考虑沥青在加载过程中发生自愈合带来的影响,今后将进行相关试验加以研究。
| [1] |
钱国平, 刘宏富, 郑健龙, 等. 沥青混合料拉压疲劳损伤试验[J]. 公路交通科技, 2012, 29(3): 1-6. QIAN Guo-ping, LIU Hong-fu, ZHENG Jian-long, et al. Experiment of Tension-compression Fatigue and Damage for Asphalt Mixture[J]. Journal of Highway and Transportation Research and Development, 2012, 29(3): 1-6. |
| [2] |
孙志林, 黄晓明. 沥青路面线性疲劳损伤特性及应力状态演变规律[J]. 公路交通科技, 2012, 29(5): 1-5, 12. SUN Zhi-lin, HUANG Xiao-ming. Linear Fatigue Damage Characteristics and Stress Evolution Regularity of Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development, 2012, 29(5): 1-5, 12. |
| [3] |
孙志林, 黄晓明, 张锐, 等. 沥青改性剂对沥青混合料疲劳性能影响研究[J]. 公路交通科技, 2008, 25(4): 33-36. SUN Zhi-lin, HUANG Xiao-ming, ZHANG Rui, et al. Study on Effect of Asphalt Modifier on Asphalt Mixtures Fatigue Performance[J]. Journal of Highway and Transportation Research and Development, 2008, 25(4): 33-36. |
| [4] |
LIAO M C, CHEN J S, TSOU K W. Fatigue Characteristics of Bitumen-filler Mastics and Asphalt Mixtures[J]. |
| [5] |
李佳, 张肖宁. 沥青混合料中胶浆疲劳破坏与变形分析[J]. 科学技术与工程, 2012, 12(35): 9585-9590. LI Jia, ZHANG Xiao-ning. Fatigue Damage and Deformation of Binder Separated from Asphalt Concrete[J]. Science Technology and Engineering, 2012, 12(35): 9585-9590. |
| [6] |
KIM Y R, LITTLE D N, SONG I. Effect of Mineral Fillers on Fatigue Resistance and Fundamental Material Characteristics:Mechanstic Evaluation[J]. Transportation Research Road, 2003, 1832: 1-8. |
| [7] |
单丽岩, 谭忆秋, 李晓琳. 沥青疲劳特性的研究[J]. 武汉理工大学学报:交通科学与工程版, 2011(1): 190-193. SHAN Li-yan, TAN Yi-qiu, LI Xiao-lin. Fatigue Characteristic of Asphalt[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering, 2011(1): 190-193. |
| [8] |
史思强, 杨玉晶, 高林. 高弹改性沥青的流变性响应[J]. 公路交通科技, 2013, 30(2): 14-18, 54. SHI Si-qiang, YANG Yu-jing, GAO Lin. Response of Rheological Behavior of Modified Asphalt with High Elasticity[J]. Journal of Highway and Transportation Research and Development, 2013, 30(2): 14-18, 54. |
| [9] |
孙大权, 林添坂, 曹林辉. 基于动态剪切流变试验的沥青疲劳寿命分析方法[J]. 建筑材料学报, 2015, 18(2): 346-350. SUN Da-quan, LIN Tian-ban, CAO Lin-hui. Evaluation Method for Fatigue Life of Asphalt Based on Dynamic Shear Rheometer Test[J]. Journal of Building Materials, 2015, 18(2): 346-350. |
| [10] |
陈浩浩, 吴少鹏, 刘全涛, 等. 沥青的疲劳性能评价方法研究[J]. 武汉理工大学学报, 2015, 37(12): 47-52. CHEN Hao-hao, WU Shao-peng, LIU Quan-tao, et al. Study on Evaluation Methods for Fatigue Property of Asphalt[J]. Journal of Wuhan University of Technology, 2015, 37(12): 47-52. |
| [11] |
袁燕. 改性沥青胶浆的疲劳性能评价[D]. 广州: 华南理工大学, 2005. YUAN Yan. Evaluation of Fatigue Performance of Modified Asphalt[D]. Guangzhou:South China University of Technology, 2005. http://d.wanfangdata.com.cn/Thesis_Y991725.aspx |
| [12] |
BHASIN A, CASTELO BRANCO V T F, MASAD E, et al. Quantitative Comparison of Energy Methods to Characterize Fatigue in Asphalt Materials[J]. Journal of Materials in Civil Engineering, 2009, 21(2): 83-92. |
| [13] |
MASAD E, CASTELO BARNCO V T F, LITTLE D N, et al. A Unified Method for the Analysis of Controlled-strain and Controlled-stress Fatigue Testing[J]. International Journal of Pavement Engineering, 2008, 9(4): 233-246. |
| [14] |
YU Jiang-miao, TSAI B W, ZHANG Xiao-ning, et al. Development of Asphalt Pavement Fatigue Cracking Prediction Model Base on Loading Mode Transfer Function[J]. Road Materials and Pavement Design, 2012, 13(3): 501-517. |
| [15] |
谢军, 郭忠印. 沥青混合料疲劳响应模型试验研究[J]. 公路交通科技, 2007, 24(5): 21-25. XIE Jun, GUO Zhong-yin. Researching on Fatigue Model of Asphalt Mixtures[J]. Journal of Highway and Transportation Research and Development, 2007, 24(5): 21-25. |
| [16] |
高爽. 沥青混合料疲劳损伤机理研究[D]. 重庆: 重庆交通大学, 2008. GAO Shuang. Research on Fatigue Damage Mechanism of Asphalt Mixture[D]. Chongqing:Chongqing Jiaotong University, 2008. http://d.wanfangdata.com.cn/Thesis/Y1250085 |
| [17] |
郑健龙, 吕松涛. 沥青混合料非线性疲劳损伤模型[J]. 中国公路学报, 2009, 22(5): 21-28. ZHEN Jian-long, LÜ Song-tao. Nonlinear Fatigue Damage Model for Asphalt Mixtures[J]. China Journal of Highway and Transport, 2009, 22(5): 21-28. |
| [18] |
朱洪洲, 严恒, 唐伯明. 沥青混合料疲劳-蠕变交互作用损伤模型[J]. 中国公路学报, 2011, 24(4): 15-20. ZHU Hong-zhou, YAN Heng, TANG Bo-ming. Damage Model of Interaction between Fatigue and Creep for Asphalt Mixture[J]. China Journal of Highway and Transport, 2011, 24(4): 15-20. |
| [19] |
UNDERWOOD B S. Multiscale Constitutive Modeling of Asphalt Concrete[D]. Raleigh:North Carolina State University, 2011. http://adsabs.harvard.edu/abs/2011phdt........14u
|
| [20] |
刘全涛. 沥青胶浆的疲劳性能研究[D]. 武汉: 武汉理工大学, 2008. LIU Quan-tao. Study on Fatigue Performance of Asphalt Mastic[D]. Wuhan:Wuhan University of Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10497-2008110560.htm |
| [21] |
吴少鹏, 江承建, 林俊涛, 等. 老化沥青胶结料的疲劳特性研究[J]. 武汉理工大学学报:交通科学与工程版, 2013, 37(3): 451-455. WU Shao-peng, JIANG Cheng-jian, LIN Jun-tao, et al. Research on Fatigue Characteristic of Aged Asphalt Binder[J]. Journal of Wuhan University of Technology:Transportation Science and Engineering Edition, 2013, 37(3): 451-455. |
 2017, Vol. 34
2017, Vol. 34
