扩展功能
文章信息
- 吕慧杰, 张诚, 刘涵奇, 罗蓉, 陈辉
- LÜ Hui-jie, ZHANG Cheng, LIU Han-qi, LUO Rong, CHEN Hui
- 沥青混合料蠕变柔量转换松弛模量的新方法
- A Novel Approach for Converting Creep Compliance into Relaxation Modulus for Asphalt Mixtures
- 公路交通科技, 2017, 34(11): 1-7
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(11): 1-7
- 10.3969/j.issn.1002-0268.2017.11.001
-
文章历史
- 收稿日期: 2017-05-31
2. 江西省交通工程集团公司, 江西 南昌 330038
2. Jiangxi Province Traffic Engineering Group Corporation, Nanchang Jiangxi 330038, China
沥青混合料是由沥青、集料和空气等按一定比例组成的黏弹性复合材料,其线性黏弹性状态下的力学性质是后续研究其损伤性质(疲劳开裂和永久变形)的基础。松弛模量作为沥青混合料的线性黏弹性性质之一,广泛用于描述沥青混合料力学响应的本构模型中,如Boltzmann叠加原理、虚应变等[1-3],因此准确确定沥青混合料的松弛模量对预测沥青路面的黏弹性力学响应具有十分重要的意义。
理论上说,沥青混合料的松弛模量可直接通过松弛试验测得,即保证沥青混合料试件各方向的轴向应变同时加载到设定值并保持不变。但由于沥青混合料自身的不均一性,松弛试验的实施具有很大的难度[4]。考虑到松弛模量和蠕变柔量是沥青混合料同一黏弹性性质的两种表现形式,两者之间可根据线性黏弹性理论进行相互转换[1, 5-6]。因此,沥青混合料的松弛模量可通过容易实施的蠕变试验测得[7]。相关研究方法已在沥青和沥青混合料上体现,例如:薛忠军等人采用沥青弯曲流变仪测得沥青的蠕变柔量,通过建立松弛模量和蠕变柔量的数值迭代表达式求解沥青的松弛模量,并根据时温等效原理绘制沥青松弛模量的主曲线[8];黄文柯等人采用万能试验机测得沥青混合料的蠕变柔量,根据松弛模量和蠕变柔量在时间域内的关系,分别运用配置法和最小二乘法求得了松弛模量Prony级数表达式的参数[9]。
上述两种方法均是基于松弛模量和蠕变柔量在时间域内的关系。本研究基于松弛模量和蠕变柔量在频率域内的关系,即复数模量与复数柔量互为倒数,提出一种新的蠕变柔量转换松弛模量的方法,并根据时温等效原理绘制沥青混合料松弛模量的主曲线,以研究沥青混合料在更广温度和时间范围内的松弛性能。
1 蠕变柔量转换松弛模量新方法 1.1 松弛模量和蠕变柔量沥青混合料作为一种典型的黏弹性材料,在小应变条件下可以被看作是线性黏弹性材料。线性黏弹性材料的松弛模量和蠕变柔量在时间域和频率域内具有如下关系,分别如式(1)和式(2)所示,且式(2)可由式(1)经由拉普拉斯变换求得[1]:
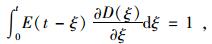
|
(1) |
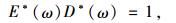
|
(2) |
式中,E(t)是松弛模量;D(t)是蠕变柔量;t是加载时间;ξ是虚拟时间变量;E*(ω)是复数模量,满足E*(ω)=E′(ω)+iE″(ω),其中E′(ω), E″(ω)分别是复数模量的实部和虚部,称作存储模量和损失模量;D*(ω)是复数柔量,满足D*(ω)=D′(ω)-iD″(ω),其中D′(ω), D″(ω)分别是复数柔量的实部和虚部,称作存储柔量和损失柔量;ω是加载频率。
根据式(2)可进一步推导出动态模量和动态柔量也成倒数关系,即:
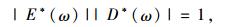
|
(3) |
式中,|E*(ω)|是动态模量,即复数模量的模,表征复数模量的大小,满足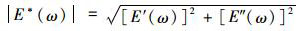
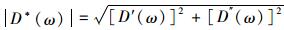
根据式(3)可推导出存储模量、损失模量、存储柔量、损失柔量满足以下关系:
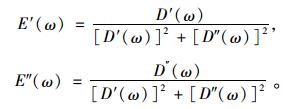
|
(4) |
式(4)是本研究提出的蠕变柔量转换成松弛模量方法的理论基础。
1.2 广义Maxwell模型和广义Kelvin模型在描述沥青混合料的松弛和蠕变性质时,通常采用弹簧和黏壶组成的力学模型进行表征。目前广泛采用广义Maxwell模型表征沥青混合料的松弛模量,采用广义Kelvin模型表征沥青混合料的蠕变柔量[10-11]。基于广义Maxwell模型的松弛模量Prony级数表达式和基于广义Kelvin模型的蠕变柔量Prony级数表达式分别如式(5)和式(6)所示:
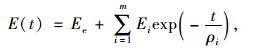
|
(5) |
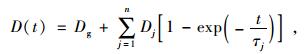
|
(6) |
式中,Ee是静弹性模量;Ei是松弛强度;ρi是松弛时间;Dg是玻璃态柔量;Dj是延迟强度,τj是延迟时间。
通过对式(5)和式(6)进行拉普拉斯变换以及运用弹性-黏弹性对应原理,可以得到存储模量、损失模量、存储柔量、损失柔量的Prony级数表达式:
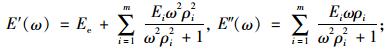
|
(7) |
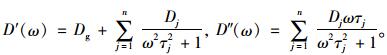
|
(8) |
且由式(5)和式(6)可进一步推出当t→0和t→∞时松弛模量需满足的边界条件:
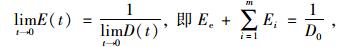
|
(9) |
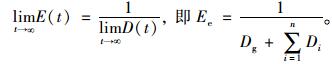
|
(10) |
本研究以式(4)作为蠕变柔量转换成松弛模量的理论基础,以式(5)~(8)作为松弛模量和蠕变柔量在时间域和频率域内的拟合模型,以式(9)和式(10)作为蠕变柔量转换成松弛模量的边界条件,提出一种蠕变柔量转换松弛模量的新方法,方法的具体步骤将在1.3节详述。
1.3 蠕变柔量转换松弛模量新方法本研究提出的蠕变柔量转换成松弛模量的方法主要包括以下5个步骤:
(1) 采用广义Kelvin模型拟合蠕变柔量的测量数据,确定广义Kelvin模型的黏弹性参数,即Dg,Dj和τj。
(2) 根据式(8)求解各角频率下的存储柔量和损失柔量,然后利用式(4)求解各角频率下的存储模量和损失模量。
(3) 根据式(10)求解广义Maxwell模型的静弹性模量,即Ee。
(4) 利用式(7)对步骤2中求得的各角频率下的存储模量和松弛模量进行拟合,以式(9)作为边界条件,求得广义Maxwell模型的其他黏弹性参数,即Ei,ρi,需要注意的是拟合需采用如式(11)所示的目标函数以充分利用存储模量和损失模量共同提供的黏弹性信息:
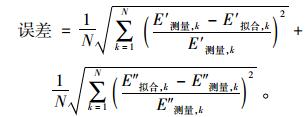
|
(11) |
(5) 将求解的Ee,Ei,ρi代入式(5)绘制松弛模量随时间的变化曲线。
为了验证蠕变柔量转换成松弛模量的方法是否可行,本研究针对2种类型的沥青混合料进行单轴压缩蠕变试验,试验方案将在第2节详述。
2 单轴压缩蠕变试验本研究针对2种类型的沥青混合料进行单轴压缩蠕变试验:①AC-13C沥青混合料,集料采用石灰岩,级配如表 1所示,沥青采用70#基质沥青,最佳油石比为4.4%;②AC-20C沥青混合料,集料采用石灰岩,级配如表 1所示,沥青采用SBS改性沥青,最佳油石比为4.3%。沥青混合料试件的制备参考《公路工程沥青及沥青混合料试验规程》(JTG E20—2011),采用旋转压实的方法成型直径为100 mm, 高度为150 mm的圆柱形试件,且保证成型后试件的空隙率控制(4.0±0.5)%范围内。
| 筛孔尺寸/mm | 26.5 | 19 | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
| 通过率/% | AC-13C | 100 | 100 | 100 | 96.4 | 81.5 | 45.2 | 30.4 | 22.0 | 16.5 | 11.5 | 8.1 | 5.4 |
| AC-20C | 100 | 97.8 | 89.5 | 78.1 | 54.4 | 34.6 | 23 | 18.8 | 13.7 | 9.5 | 7.1 | 5.5 | |
在试件成型后,利用MTS多功能材料试验机对试件进行单轴压缩蠕变试验。为了研究不同温度下沥青混合料的松弛性质,试验在0,10,20,30,40 ℃共5个温度下进行,加载时间均设定为120 s。每个温度下的蠕变试验所施加的轴向力均需保证试验结束后试件的累积应变控制在150 με以内,以确保沥青混合料处于线性黏弹性阶段[12]。对每种沥青混合料均采用2个试件进行平行试验,各温度下蠕变试验的结果取2个试件的平均值。以AC-13C沥青混合料为例,绘制其各个试验温度下的蠕变柔量曲线,如图 1所示。
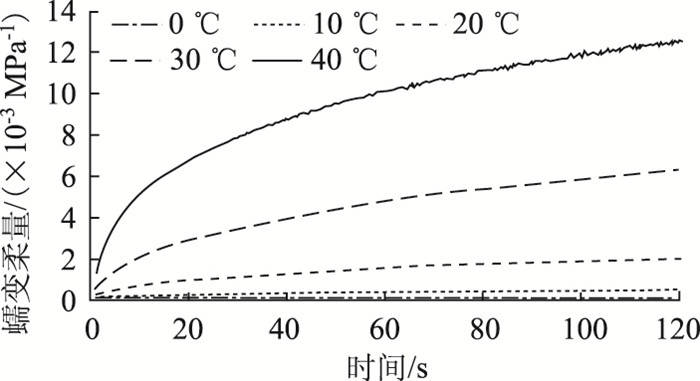
|
| 图 1 沥青混合料各温度下蠕变柔量测量曲线 Fig. 1 Measured creep compliance curves of asphalt mixture at different temperatures |
| |
需要注意的是蠕变试验加载时仪器需1 s的时间才能达到指定的应力水平,故有效测量数据从第1 s开始。在测得沥青混合料在各温度下的蠕变柔量后,第3节将根据本研究提出的方法求解各温度下的松弛模量并绘制松弛模量主曲线。
3 求解松弛模量并绘制松弛模量主曲线 3.1 单一温度下松弛模量求解在得到各个试验温度下蠕变柔量的测量数据后,采用广义Kevin模型对蠕变柔量测量数据进行最小二乘法拟合。由于蠕变试验时长较短,在进行拟合时,取n=2并将Dg,D1,D2,τ1,τ2均看作拟合参数,各温度下蠕变柔量拟合参数(即黏弹性参数)如表 2所示,其中AC-13C沥青混合料最终求得的拟合曲线如图 2所示。由表 2知,各温度下蠕变柔量拟合结果的判定系数均大于0.999,由此证明广义Kelvin模型可以很好地表征沥青混合料的蠕变性质。
| 混合料 | 温度/℃ | Dg/(×10-3MPa-1) | D1/(×10-3MPa-1) | τ1/s | D2/(×10-3MPa-1) | τ2/s | R2 |
| AC-13 | 0 | 0.048 9 | 0.030 7 | 5.786 2 | 0.072 5 | 68.927 1 | 0.999 6 |
| 10 | 0.081 9 | 0.097 8 | 6.791 1 | 0.456 7 | 120.904 | 0.999 6 | |
| 20 | 0.201 7 | 0.400 4 | 8.426 8 | 2.214 8 | 112.607 | 0.999 8 | |
| 30 | 0.452 28 | 1.358 4 | 7.206 6 | 5.972 6 | 86.930 5 | 0.999 7 | |
| 40 | 1.219 6 | 3.497 6 | 6.597 7 | 9.629 6 | 72.589 6 | 0.999 4 | |
| AC-20 | 0 | 0.057 04 | 0.037 66 | 6.429 8 | 0.090 0 | 80.735 4 | 0.999 6 |
| 10 | 0.102 3 | 0.116 5 | 6.937 0 | 0.486 3 | 100.591 | 0.999 8 | |
| 20 | 0.237 1 | 0.505 2 | 7.251 8 | 1.832 8 | 84.282 7 | 0.999 8 | |
| 30 | 0.645 7 | 1.691 4 | 7.456 7 | 4.619 6 | 86.740 5 | 0.999 7 | |
| 40 | 1.536 8 | 3.616 3 | 6.183 5 | 9.243 2 | 76.402 9 | 0.999 3 |
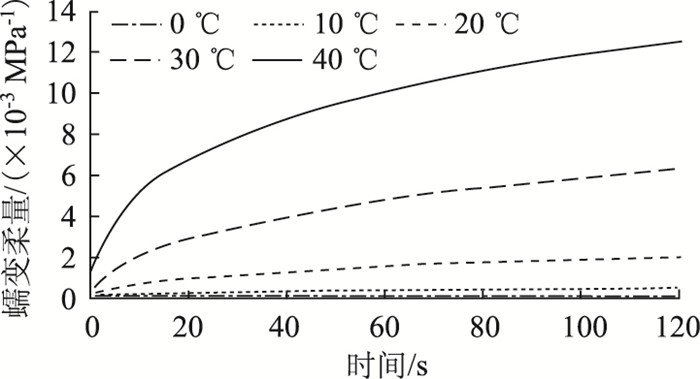
|
| 图 2 沥青混合料各温度下蠕变柔量拟合曲线 Fig. 2 Fitted creep compliance curves of asphalt mixture at different temperatures |
| |
在确定广义Kelvin模型的黏弹性参数后,根据式(8)求解各角频率下的存储柔量和损失柔量,其中时间和角频率的转换采用Schapery提出的近似方法ω=1/(2t)[13]。考虑到蠕变试验加载时仪器需1 s的时间达到指定的应力水平,且前5 s的蠕变试验数据受到瞬时效应的影响[14-15],因此选取5~120 s之间的蠕变数据转换至存储柔量和损失柔量,对应的频率域内的范围为4.167×10-3~0.1 rad/s。在确定损失柔量和存储柔量后,根据式(4)求解4.167×10-3~0.1 rad/s范围内的损失模量和存储模量。然后采用式(7)所示的存储模量和损失模量的Prony级数表达式对求解的损失模量和存储模量进行拟合,取m=2,其中静弹性模量Ee可根据式(10)直接求出,松弛强度E1,E2和松弛时间ρ1,ρ2需采用式(11)所示的误差方程求解,且在拟合的过程中需满足式(9)所示的边界条件。最终求得的各温度下松弛模量的黏弹性参数如表 3所示,并以AC-13C沥青混合料为例绘制松弛模量曲线,如图 3所示。
| 混合料 | 温度/℃ | Ee/MPa | E1/MPa | ρ1/s | E2/MPa | ρ2/s |
| AC-13 | 0 | 6 532.705 9 | 8 255.159 9 | 3.171 5 | 5 275.846 2 | 36.838 9 |
| 10 | 1 571.382 0 | 7 431.816 9 | 2.695 8 | 3 214.155 5 | 36.647 3 | |
| 20 | 355.000 3 | 3 791.589 | 2.262 4 | 810.767 8 | 28.676 9 | |
| 30 | 128.481 8 | 1 837.550 7 | 1.459 5 | 244.983 3 | 24.685 5 | |
| 40 | 69.702 3 | 656.917 6 | 1.464 5 | 93.306 4 | 27.279 7 | |
| AC-20 | 0 | 5 413.493 9 | 7 501.501 4 | 3.413 9 | 4 616.190 9 | 42.028 1 |
| 10 | 1 418.250 0 | 5 867.676 0 | 2.791 3 | 2 486.539 3 | 33.590 1 | |
| 20 | 388.330 5 | 3 197.942 4 | 1.943 8 | 630.856 7 | 27.929 9 | |
| 30 | 128.481 8 | 1 837.550 7 | 1.459 5 | 244.983 4 | 24.685 5 | |
| 40 | 69.462 1 | 491.335 7 | 1.629 7 | 89.910 8 | 30.180 3 |
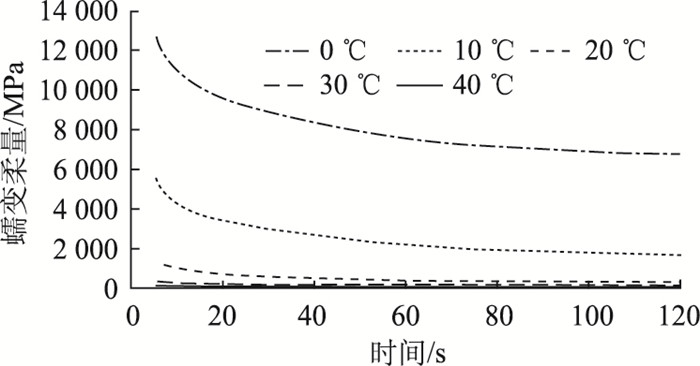
|
| 图 3 沥青混合料各温度下松弛模量曲线 Fig. 3 Relaxation modulus curves of asphalt mixture at different temperatures |
| |
为了验证本研究提出的蠕变柔量转换松弛模量方法的准确性,采用式(1)所示的时间域内蠕变柔量和松弛模量的关系进行评价。令h(t)表征式(1)的左式,即:
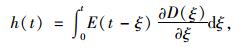
|
(12) |
然后将广义Maxwell模型和广义Kelvin模型的Prony级数表达式代入式(12)可得:
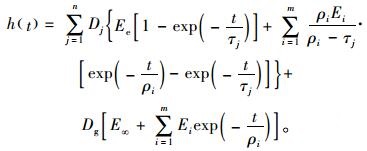
|
(13) |
式(13)中的所有参数均已求解并汇总于表 2和表 3,将各参数值代入式(13)并将求解的结果与数值1进行比较计算误差,即误差函数的表达式为:
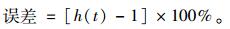
|
(14) |
利用公式(14)计算2种沥青混合料各温度下蠕变柔量转换松弛模量的误差,并以AC-13C为例绘成如图 4所示的误差曲线图。由图 4可知,采用本研究提出的方法进行蠕变柔量到松弛模量的转换,误差绝对值控制在1.4 %以内,且误差随着加载时间增长而减小,由此证明文中提出的方法的可行性。
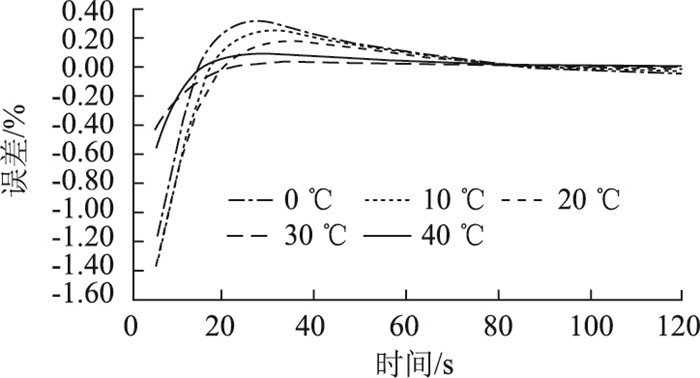
|
| 图 4 沥青混合料蠕变柔量转换松弛模量误差曲线 Fig. 4 Error curves of converting creep compliance into relaxation modulus of asphalt mixture |
| |
3.2 绘制松弛模量主曲线
沥青混合料作为一种典型的黏弹性材料,其松弛性质与温度和时间相关。为了研究沥青混合料在更广温度和时间范围内的松弛性质,可以采取绘制沥青混合料松弛模量主曲线的方法。绘制松弛模量主曲线的理论基础是时温等效原理,时温等效原理认为:对热流变简单材料,如处于线性黏弹性阶段的沥青混合料,以试验温度和参考温度下的松弛模量做对比,当试验温度低于参考温度时,该试验温度对参考温度下松弛模量的影响相当于在参考温度下缩短试验时间;当试验温度高于参考温度时,该试验温度对参考温度下松弛模量的影响相当于在参考温度下延长试验时间[16-17]。采用数学表达式对时温等效原理进行表达,具体公式如下:
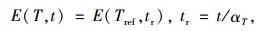
|
(15) |
式中,T是试验温度;t是试验加载时间;E(T, t)是试验温度和试验加载时间下测得的松弛模量;Tref是指定的参考温度;tr是缩减时间;E(Tref, tr)是参考温度和缩减时间下的松弛模量;αT是移位因子。
根据时温等效原理,本研究采用Sigmoidal函数作为主曲线的拟合模型,采用Arrhenius方程作为移位因子方程绘制沥青混合料松弛模量主曲线。Sigmoidal函数和Arrhenius方程的表达式分别如下所示[18-20]:
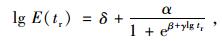
|
(16) |
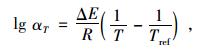
|
(17) |
式中,δ是松弛模量在对数坐标系下的最小值;α是松弛模量在对数坐标系下最大值与最小值之差;β和γ是形状参数;ΔE是活化能;R是通用气体常数;T和Tref分别是开尔文温度标下的试验温度和参考温度。
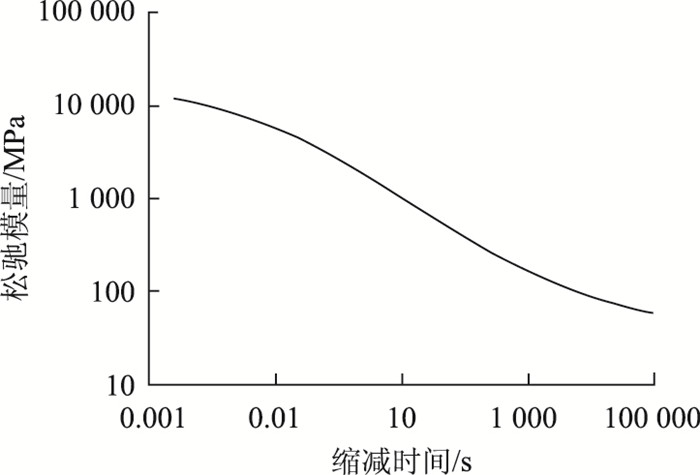
确定主曲线模型和移位因子方程后,选取20 ℃作为参考温度,采用式(16)和式(17)对不同温度下的松弛模量数据进行拟合,根据不同温度下的移位因子,将5个温度下的松弛模量曲线进行横向平移得到松弛模量主曲线,并以AC-13C沥青混合料为例,绘制如图 5所示的主曲线。由图 5知,通过绘制沥青混合料松弛模量主曲线可以获取更广时间范围的松弛性质,因此可以更加全面地描述沥青混合料的黏弹性性质,更加准确地预测沥青路面的黏弹性力学响应。
|
| 图 5 沥青混合料松弛模量主曲线(参考温度:20 ℃) Fig. 5 Relaxation modulus master curve of asphalt mixture (reference temperature: 20 ℃) |
| |
4 结论
(1) 对AC-13C和AC-20C两种沥青混合料在5个温度下分别进行单轴压缩蠕变试验,采用基于广义Kelvin模型的Prony级数表达式对各温度下蠕变柔量测量数据进行拟合,拟合结果显示判定系数均大于0.999,表明广义Kevin模型能很好地表征沥青混合料的蠕变性能。
(2) 根据松弛模量和蠕变柔量在频率域的关系,即复数模量和复数柔量互为倒数,提出一种蠕变柔量转换松弛模量的新方法,并采用该方法求解了两种沥青混合料在不同温度下的松弛模量。采用松弛模量和蠕变柔量在时间域内的关系验证提出方法的准确性,验证结果显示误差绝对值控制在1.4%以内,由此证明了提出方法的可行性和准确性。
(3) 根据时温等效原理,采用Sigmoidal函数作为松弛模量主曲线的拟合模型、Arrhenius方程作为移位因子方程,绘制了两种沥青混合料松弛模量的主曲线,由此可以获取更广时间和温度范围内的沥青混合料松弛性质,从而更加全面地描述沥青混合料的黏弹性性质。
| [1] |
PARK S W, SCHAPERY R A. Methods of Interconversion between Linear Viscoelastic Material Functions. Part Ⅰ:A Numerical Method Based on Prony Series[J]. International Journal of Solids and Structures, 1999, 36(11): 1653-1675. |
| [2] |
SCHAPERY R A. Correspondence Principles and a Generalized J Integral for Large Deformation and Fracture Analysis of Viscoelastic Media[J]. International Journal of Fracture, 1984, 25(3): 195-223. |
| [3] |
赵延庆, 黄大喜, 潘有强. 利用虚应变分析沥青混合料的粘弹性质[J]. 重庆交通大学学报:自然科学版, 2008, 27(2): 236-239. ZHAO Yan-qing, HUANG Da-xi, PAN You-qiang. Analysis on Viscoelasticity of Asphalt Mixtures Using Pseudo Strain[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2008, 27(2): 236-239. |
| [4] |
赵延庆, 唐积民, 白龙. 利用沥青混合料复数模量确定松弛模量研究[J]. 建筑材料学报, 2012, 15(4): 498-502. ZHAO Yan-qing, TANG Ji-min, BAI Long. Determination of Relaxation Modulus Using Complex Modulus of Asphalt Mixture[J]. Journal of Building Materials, 2012, 15(4): 498-502. |
| [5] |
刘孝敏, 唐志平, 李欣增. 复柔量-蠕变柔量和复模量-松弛模量转换公式的讨论[J]. 中国科学技术大学学报, 1989(4): 476-485. LIU Xiao-min, TANG Zhi-ping, LI Xin-zeng. Discussion on Transformation Formulas between Complex Compliance and Creep Compliance, Complex Modulus and Relaxation Modulus in Linear Viscoelasticity[J]. Journal of University of Science and Technology of China, 1989(4): 476-485. |
| [6] |
KIM J, SCHOLAR G A, KIM S. Determination of Accurate Creep Compliance and Relaxation Modulus at a Single Temperature for Viscoelastic Solids[J]. Journal of Materials in Civil Engineering, 2008, 20(2): 147-156. |
| [7] |
程永春, 许淳, 梁春雨, 等. 沥青混合料蠕变柔量的试验研究与力学解析[J]. 吉林大学学报:工学版, 2008(增2): 70-73. CHENG Yong-chun, XU Chun, LIANG Chun-yu, et al. Experimental Study and Mechanical Analysis on the Creep of the Asphalt Mixture[J]. Journal of Jilin University:Engineering and Technology Edition, 2008(S2): 70-73. |
| [8] |
薛忠军, 张肖宁, 詹小丽, 等. 基于蠕变试验计算沥青的低温松弛弹性模量[J]. 华南理工大学学报:自然科学版, 2007, 35(2): 64-68. XUE Zhong-jun, ZHANG Xiao-ning, ZHAN Xiao-li, et al. Calculation of Low-temperature Relaxed Modulus of Elasticity for Bitumen via Creep Test[J]. Journal of South China University of Technology:Natural Science Edition, 2007, 35(2): 64-68. |
| [9] |
黄文柯, 张丽娟, 张肖宁, 等. 沥青混合料蠕变柔量转换为松弛模量的研究[J]. 交通科学与工程, 2015, 31(3): 7-12. HUANG Wen-ke, ZHANG Li-juan, ZHANG Xiao-ning, et al. Research on the Relaxation Modulus Converted to Creep Compliance of Asphalt Mixture[J]. Journal of Transport Science and Engineering, 2015, 31(3): 7-12. |
| [10] |
ZHAO Yan-qing, NI Yuan-bao, ZENG Wei-qiao. A Consistent Approach for Characterising Asphalt Concrete Based on Generalised Maxwell or Kelvin Model[J]. Road Materials and Pavement Design, 2014, 15(3): 674-690. |
| [11] |
SUN Yi-ren, HUANG Bao-shan, CHEN Jing-yun. A Unified Procedure for Rapidly Determining Asphalt Concrete Discrete Relaxation and Retardation Spectra[J]. Construction and Building Materials, 2015, 93: 35-48. |
| [12] |
LEVENBERG E, UZAN J. Triaxial Small-strain Viscoelastic-viscoplastic Modeling of Asphalt Aggregate Mixes[J]. Mechanics of Time-Dependent Materials, 2004, 8(4): 365-384. |
| [13] |
SCHAPERY R A. A Method of Viscoelastic Stress Analysis Using Elastic Solutions[J]. Journal of the Franklin Institute, 1965, 279(4): 268-289. |
| [14] |
LUO Rong, LYTTON R L. Characterization of the Tensile Viscoelastic Properties of an Undamaged Asphalt Mixture[J]. Journal of Transportation Engineering, 2010, 136(3): 173-180. |
| [15] |
ZHANG Yu-qing, LUO Rong, LYTTON R L. Anisotropic Viscoelastic Properties of Undamaged Asphalt Mixtures[J]. |
| [16] |
WALUBITA L F, ALVAREZ A E, SIMATE G S. Evaluating and Comparing Different Methods and Models for Generating Relaxation Modulus Master-curves for Asphalt Mixes[J]. Construction and Building Materials, 2011, 25(5): 2619-2626. |
| [17] |
YUSOFF N I M, SHAW M T, AIREY G D. Modelling the Linear Viscoelastic Rheological Properties of Bituminous Binders[J]. Construction and Building Materials, 2011, 25(5): 2171-2189. |
| [18] |
ZHU Hao-ran, SUN Lu, YANG Jun, et al. Developing Master Curves and Predicting Dynamic Modulus of Polymer-modified Asphalt Mixtures[J]. Journal of Materials in Civil Engineering, 2011, 23(2): 131-137. |
| [19] |
FOROUGH S A, NEJAD F M, KHODAⅡ A. A Comparative Study of Temperature Shifting Techniques for Construction of Relaxation Modulus Master Curve of Asphalt Mixes[J]. Construction and Building Materials, 2014, 53(53): 74-82. |
| [20] |
YUSOFF N I M, CHAILLEUX E, AIREY G D. A Comparative Study of the Influence of Shift Factor Equations on Master Curve Construction[J]. International Journal of Pavement Research and Technology, 2011, 4(6): 324-336. |
 2017, Vol. 34
2017, Vol. 34
