扩展功能
文章信息
- 江志娟, 关高峰
- JIANG Zhi-juan, GUAN Gao-feng
- “一带一路”倡议下的国际通道中转枢纽设计模型和算法
- A Model and an Algorithm for Designing Transit Hub of International Channel under the Belt and Road Initiative
- 公路交通科技, 2017, 34(10): 135-143, 151
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(10): 135-143, 151
- 10.3969/j.issn.1002-0268.2017.10.019
-
文章历史
- 收稿日期: 2016-11-29
2. 长江大学 管理学院, 湖北 荆州 434023
2. School of Management, Yangtze University, Jingzhou Hubei 434023, China
“一带一路”倡议是我国对外开放、全域发展的重要方略,为亚欧贸易合作开辟了新的途径。新亚欧大陆桥作为亚欧贸易最便捷的陆上国际通道,是我国与沿线国家贸易合作的重要通道,中欧班列的开通更是为中欧贸易提供了快速通道。然而,中欧贸易货源不足、中欧班列间货源竞争致使贸易成本增加,因此2016年10月17日国家发改委发布了《中欧班列发展规划(2016—2020)》(以下简称《规划》),为三大通道的中欧班列划分了货源吸引区域。进一步,在中欧贸易货源不足的情况下,需要建设中欧班列的中转枢纽,吸引区域内货物的集中、分拣、分装,以保障由中转枢纽发至欧洲的班列满载出行。《规划》中提出了中欧班列开行的三大通道货源吸引区,这里以西部通道为例,提出国家通道中转枢纽的设计方法。
西部通道涵盖西北、西南、华中、华南等地区,经陇海、兰新等铁路干线运输。西部通道货源吸引区域涵盖了丝绸之路经济带的大部分省份,依托新亚欧大陆桥实现中欧贸易往来。而合理选择西部通道的枢纽节点,有助于提高货物运输质量和效率,增强与“一带一路”沿线国家的贸易往来。董千里等[1]通过对“一带一路”中欧国际班列运行问题的分析,认为国际中转枢纽港地位和功能缺失是制约中欧班列集成运行系统形成的关键因素。在进行枢纽节点规划中,不仅要考虑运输成本和效率,更应重视降低运输过程对环境的影响。2016年11月4日《巴黎协议》正式生效,降低温室气体排放和促进可持续发展已成为全球问题,各缔约国需要根据协议的规定采取减缓措施。因此温室气体排放已成为全球关注的焦点问题,特别是枢纽的建设过程中需要考虑枢纽及运输过程中所产生的温室气体排放量,以缓解运输过程对环境产生的影响,实现可持续发展。
国内已有诸多学者研究了联运枢纽的选址和优化。张琦[2]采用引力模型构建了联运组织的优化模型。陈沿伊[3]以总成本最小化为目标函数建立了联合货物运输枢纽布局优化模型。王清斌[4]以最小化运输总成本为目标函数建立了货流分配优化模型。尹莉以总成本最小化为目标函数构建了货物枢纽选址模型[5]。国内学者在枢纽选址方面的研究[6-7],侧重于以成本为目标函数的枢纽选址模型,较少考虑枢纽及运输过程对环境的影响。在国外,R. Z. Farahani等[8]在总结近年来对枢纽选址问题的研究中,指出枢纽选址模型的可持续性是一个重要的发展趋势,特别是考虑社会和环境的影响,然而在这方面的研究相对较少。M. Mohammadi等[9]开始关注温室气体排放和噪音污染对枢纽选址的影响,构建了可持续选址模型。S. L. Lam等[10]在研究中引入碳排放限制。国外学者在枢纽选址模型的构建中开始关注枢纽对周边交通的影响,但研究中较少关注运输路径上的温室气体排放,以及运输方式的选择对成本、时间和温室气体排放量的综合影响。因此,本研究基于“一带一路”发展战略,依据规划中提出的西部通道货源吸引区域,考虑降低成本、提高效率和减少温室气体排放量3个指标,进行可持续的公铁联运枢纽节点布局。
1 可持续联运枢纽配置模型设计 1.1 问题描述与模型假设中欧班列西部通道货源吸引范围内的主要货源节点城市包括昆明、贵阳、重庆、成都、西安、兰州、西宁、银川8个省会城市。而西部通道通过新疆的阿拉山口、霍尔果斯口岸处境运往欧洲,而乌鲁木齐是西部通道通向欧洲的必经之地,为便于境内联运枢纽研究,这里将乌鲁木齐作为货物通向欧洲市场的目的地。相对于中、东部通道,西部通道货源吸引区域的主要节点城市分散、交通基础设施不健全,从而影响中欧班列的运输效率。联合运输中转枢纽作为衔接多种运输方式的中转站,通过其选址和运输方式选择的决策,可降低联合运输成本、提高运输效率、降低温室气体排放。
文中在枢纽无容量限制的情况下,目的地城市为乌鲁木齐,用C0表示。记货源城市的集合为C={1, 2, …, m},即m=8个货源城市,假设每个城市建有1个公路货运节点和1个铁路货运节点,故所有货源城市的货运节点为n=16个。C=8表示城市的个数,所有节点的集合为N,N={1, 2, …, m, m+1, …, n},其中D={1, 2, …, m}表示公路节点的集合,R={m+1, m+2, …, n}表示铁路节点的集合。对于任意城市i(i∈C),其公路节点表示为i,铁路节点表示为m+i。
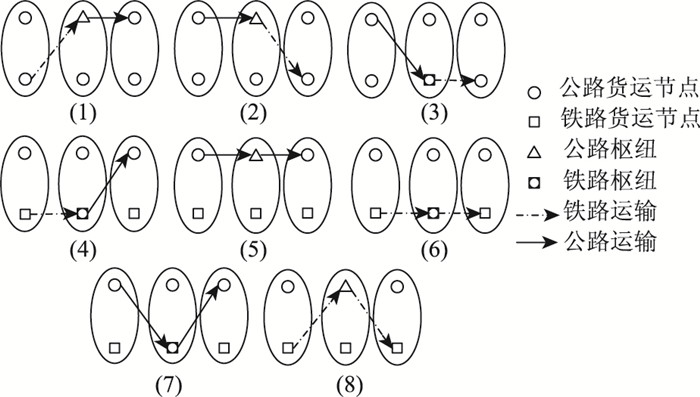
联运枢纽与其连接的运输方式之间存在8种关系,如图 1所示,其中(5)~(8) 属于非联合运输;(5) 和(6) 的枢纽两端连接的是同一种运输方式,如果所有货源城市到枢纽城市的运输方式与枢纽到需求城市的运输方式相同,则枢纽为单一运输方式的枢纽,例如(5) 为公路枢纽,(6) 为铁路枢纽,这里将(5) 和(6) 的形式作为联运枢纽配置的特殊形式。而(7) 和(8) 在现实中属于欠合理的情形,因此,尽量避免这样的形式。
|
| 图 1 联运枢纽中转形式 Fig. 1 Transit forms in intermodal hub |
| |
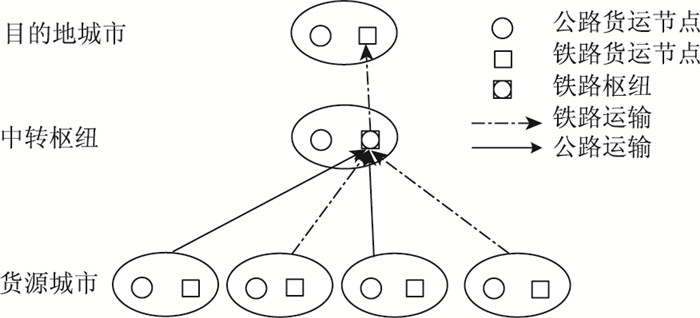
考虑到中转枢纽的中转货运量相对较大,且西部通道出口主要依靠铁路通道,因此,在中转枢纽选择中只考虑建设铁路枢纽,通向目的地的运输方式选择铁路运输方式,所以,这里只考虑如图 1中的(3) 和(6) 两种情况。货源城市、中转枢纽与目的地城市之间的一般关系形式如图 2所示。
|
| 图 2 联合运输的一般形式 Fig. 2 General form of intermodal transport |
| |
基本假设条件如下:
(1) 每个城市只能建立1个枢纽,中转枢纽只能为铁路枢纽。
(2) 假设枢纽容量无限制。
(3) 由于货车在枢纽上的等待排队和运输过程中,产生温室气体的排放,而对环境产生一定的影响。
(4) 计算温室气体排放率时着重考虑运载工具(如重量、阻力系数等)的影响。
(5) 货源城市的所有货物通过1个中转枢纽转运至目的地城市,不存在直达运输的情况。
(6) 车辆在所有枢纽上的等待时间、到达速率、服务窗口个数、服务速率和每辆货车每分钟消耗的功率等参数均相同。
1.2 目标函数 1.2.1 成本函数总成本函数C(X)由运输成本和枢纽建设成本构成(X为枢纽位置),总成本最小化目标函数如式(1) 所示。
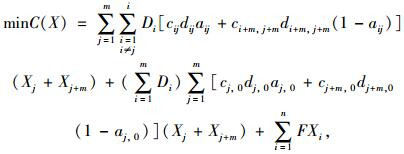
|
(1) |
式中,Di(i=1, 2, …, m)为货源城市i的发运量;cij和dij分别为城市i与j之间的单位公路运输成本和公路运输距离;ci+m, j+m和di+m, j+m分别为城市i与j之间的单位铁路运输成本和铁路运输距离;cj, 0和dj, 0分别为城市j到目的地的单位公路成本和公路运输距离;cj+m, 0和dj+m, 0分别为城市j到目的地的单位铁路运输成本和铁路运输距离;aij和aj, 0是0-1变量,aij为城市i与j之间运输方式的选择,当aij=1时,为两个城市之间采用公路运输方式,当aij=0时,为两个城市之间采用铁路运输方式,aj, 0为城市j与目的地之间运输方式的选择,同理,aj, 0=1为城市j与目的地之间采用公路运输方式,aj, 0=0为城市j与目的地之间采用铁路运输方式;Xj和Xj+m是枢纽选址变量,当Xj=1时,为在城市j建设公路枢纽,当Xj+m=1时,为在城市j建设铁路枢纽。
S.A.Alumur等[11]通过实例验证了城市的枢纽建设成本与源于该枢纽城市的货量有关,枢纽建设成本为Fk∈[10lnDk, 20lnDk], ∀k,即在10lnDk和20lnDk之间随机抽取数据作为枢纽k的固定建设成本,其中Dk为源于枢纽城市k的货量。据此,式(1) 中的F为随机数,由于中转枢纽的货运量为所有货源节点城市的货运量总和,则各城市建设枢纽的固定成本相同,均为F∈[10lnD, 20lnD],其中D为货运总量。
1.2.2 时间函数总时间函数T(X)由运输时间和枢纽中转时间构成,总时间最小化目标函数为:

|
(2) |
式中, vij和vi+m, j+m分别为城市i与j之间的公路和铁路运输速度;vj, 0和vj+m, 0分别为城市j到目的地的公路和铁路运输速度;tdd为公路转公路的中转时间;tdr为公路转铁路的中转时间;trr为铁路转铁路的中转时间。
1.2.3 温室气体排放函数在进行温室气体排放研究的过程中,只考虑由于交通工具的重量和载货量而引起的温室气体排放量,将总的温室气体排放量分为路径上的温室气体排放量和枢纽上的温室气体排放量。由于路径上的温室气体排放量由能源消耗量表达,枢纽上的温室气体排放量由功率消耗量表达,两个量的量纲不同,故将温室气体排放函数分解为路径和枢纽上的温室气体排放函数,分别为GHG(X)和THE(X)。
(1) 路径上的温室气体排放量
动机瞬间发动温室气体的排放速率与燃料使用率Fe之间存在线性相关关系[9, 12],M.Mohammadi等[9]用Fe反映温室气体的排放速率,其计算式为:

|
(3) |
式中,q为发动机摩擦系数;N为发动机转速;V为发动机排量;ε为车辆传动效率;η为柴油机效率; U为常量,其值取决于包括在内的常量;Pa为发动机运行及其车辆附件(空调等)损耗的功率;Pt为车辆总消耗功率,其计算式为:
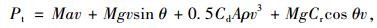
|
(4) |
式中,M为车辆总质量;a为车辆加速度;v为车辆的行驶速度;g为重力系数;θ为路角;θij为弧(i, j)的路角,当道路平坦时,路角为0;Cd为阻力系数;Cr为滚动阻力系数;A为车辆的表面积;ρ为空气密度。
进一步,推导出每辆车在城市节点之间消耗的能源总量为Pij,近似计算式为:
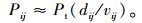
|
(5) |
本研究旨在比较各枢纽的建设对周边环境所造成的影响。由于城市之间公路或铁路的路况相对复杂,且存在诸多不确定因素(如道路施工),故假设所有城市之间的公路或铁路都是平坦的,即假设θ=θij=0,同时,考虑在研究路线上有两种运输方式可供选择,即公路运输方式和铁路运输方式。假设公路上卡车在节点之间行驶的速度为vij,1辆卡车的总负载质量M=EW+LW,其中EW为卡车的空载质量,LW为卡车的载货量。由于能量消耗与温室气体的排放之间存在线性正相关关系,故这里将温室气体排放量近似为能源消耗。由此,得到节点之间公路运输的温室气体排放量GHGijd为:
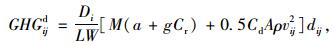
|
(6) |
令α=a+gCr,β=0.5CdAρ,则式(6) 转化为式(7):
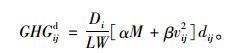
|
(7) |
铁路运输中牵引机车包括内燃机车和电力机车,电力机车耗油量为0,因此,只有内燃机车因耗油而产生温室气体。假设铁路内燃机车所占比例为δ,铁路内燃机车每吨公里耗油量为γ,则铁路运输路径上节点之间的温室气体排放量为GHGijr为:

|
(8) |
由此,运输路径上的温室气体排放量最小化目标函数为:
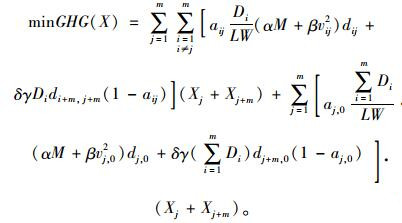
|
(9) |
(2) 枢纽上的温室气体排放量
火车在进入到枢纽后即停在枢纽上,从城市边缘到停放在枢纽上的温室气体排放量相对于卡车在城市交通中造成的温室气体排放量小得多,同时,相对于路径上的温室气体排放量也小得多,故在这里忽略不记(不考虑让车等待的情况)。故只有在公路枢纽上,由于汽车要穿越城市街道,在穿越过程中会有交通拥堵等现象,而致使车辆的温室气体排放量相对较大。因此,枢纽上的温室气体排放量,只考虑公路运输方式在枢纽上产生的温室气体排放量而忽略铁路枢纽的温室气体排放量。因为在计算中考虑使用统一的卡车车型,所以,枢纽上的尾气排放量和卡车数量与卡车在枢纽上的等待时间相关(这里的等待时间包括卡车在枢纽城市市区内的通行时间)。
由于卡车到枢纽的数目和频率随着卡车的到达时间变化,如环境条件、交通拥堵、链路中段等事件的发生,使得卡车进入枢纽的等待时间服从泊松分布,卡车到达枢纽节点的数量服从泊松分布[13-15]。车辆到达枢纽服从参数为λ的泊松分布,每辆车的服务时间服从参数为μ的泊松分布,故构成M/M/c排队模型。车辆由于消耗功率而引起温室气体的排放,因此,温室气体总的排放量THE近似等于所有车辆消耗的功率:
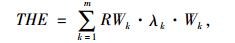
|
(10) |
式中,RWk为枢纽k上每辆货车每分钟消耗的功率;λk为枢纽k上的货车到达速率;Wk为枢纽k上的等待时间,其计算式为:

|
(11) |
式中,μk为枢纽k的服务速率;ck为在枢纽k服务供应商的数量。
假设车辆在所有节点上的等待时间、到达速率、服务窗口个数、服务速率和每辆货车每分钟消耗的功率等参数均相同,即RWk, λk, ck, μk为定值,由此,枢纽上的温室气体排放量最小化目标函数为:
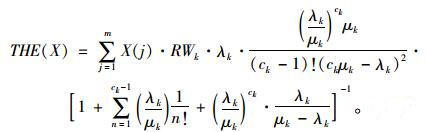
|
(12) |
式(13)~(18) 构成多目标非线性0-1规划模型,是可持续联运枢纽配置模型。

|
(13) |

|
(14) |

|
(15) |

|
(16) |

|
(17) |

|
(18) |
评价函数由总成本、总时间、运输路径和枢纽上温室气体排放量4个函数构成。假设成本、时间、路径上温室气体排放量、枢纽上温室气体排放量在总评价函数中所占比重分别为w1, w2, w3, w4,为统一量纲,分别对各子目标函数取正切,总目标函数为:
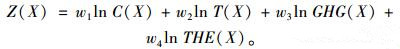
|
(19) |
m个货源城市之间存在复杂的公路和铁路交通网络,需在m个货源城市之中选择1个城市建设公路枢纽或铁路枢纽。该问题属于组合优化问题,设所有状态构成的解空间Ω={s1, s2, …, sm, sm+1, …, sn},Z(si)为状态si对应的目标函数值,组合优化问题是要寻求最优解s*[16],使得∀si∈Ω, Z(s*)=minZ(si), i=1, 2, …, n。在该问题中,si为选择货运节点i是枢纽的状态,s*为枢纽的最佳位置。
2.2 算法设计假设该问题的解空间Ω={1, 2, …, m, m+1, …, n},j, j+m(i=1, 2, …, m)分别为公路和铁路货运节点,从n个货运节点中随机抽取1个货运节点k∈Ω作为枢纽节点,Xk为枢纽选址变量,Xk=1时,表示选择k为枢纽节点。计算其目标函数值Z(Xk),得到最优解X*。
本问题中还涉及到运输方式选择变量aij,令A=(aij)m×m,在计算目标函数值时,随机生成一个m×n的0-1矩阵A0作为运输方式选择变量的初始值,进一步对A0进行随机扰动产生新的矩阵,计算新的目标函数值,将新的目标函数值与初始目标函数值进行比较,选择目标函数值小的矩阵作为新的运输方式选择矩阵。以此类推,直到搜索到使目标函数值最小的运输方式选择矩阵。在该问题中,可行解的个数为n个,每个可行解对应的可能的运输方式组合有2m种,如果用枚举法则需要n×2m种组合方案,数量较大。当n的值充分大时,为大规模的组合优化问题,则成为NP-hard问题,因此,适合于运用启发式算法进行求解,这里采用模拟退火算法。
模拟退火算法设计如下:
2.2.1 初始值设置设置初始可行解和运输方式选择矩阵。(1) 从{1, 2, …, m, m+1, …, n}中随机抽取k,令Xk=1,产生初始解X0;(2) 随机生成0-1矩阵A0=(aij)(m+1)×m,其中,第m+1行表示aj, 0,即各货运节点到目的地的运输方式;(3) 计算目标函数值Z0(X0)。初始温度t0=(Zmin-Zmax)/lnP0,其中Zmin和Zmax为随机产生L个可行解中的最小目标函数值和最大目标函数值;P0为初始解的可接受概率,P0的取值足够小,即其成为最优解的可能性极小,进而在更大的解空间内搜索最优解。温度下降策略采用tk+1=0.99tk,其中k为迭代次数,tk和tk+1分别为k和k+1次迭代的温度。
2.2.2 搜索候选解对矩阵A0分别进行1,2,3, …,m个位置的0-1变换扰动,假设扰动的次数为r次,产生运输方式选择矩阵Ar,通过随机扰动产生一个新的候选解X′,新解的目标函数值为Z(X′),比较新解的目标函数值与原目标函数值的大小,如果Z(X′)≤Z(X),则接受新解为候选解,否则根据Metropolis准则[17-18]计算
获得候选解的同时产生一个新的温度T′。随着温度的下降搜索更好的解,直到温度下降到最低温度,得到问题的最优解。这里采用的温度下降策略公式为:

|
(20) |
因此,随着温度的下降,不断产生更优的目标函数值,直到得到最优解。
3 算例 3.1 参数设置根据规划中提出的三大通道货源吸引范围,西部通道吸引范围内的货源节点城市包括昆明、贵阳、重庆、成都、西安、兰州、西宁、银川、拉萨、乌鲁木齐。由于乌鲁木齐市是西部通道的必经之地,因此将乌鲁木齐模拟为出口的目的地,货源节点城市为除拉萨之外的昆明、贵阳、重庆、成都、西安、兰州、西宁、银川8个城市。以西部通道吸引区域中的8个城市作为货源节点,以乌鲁木齐作为目的地,从8个货源节点城市中选择1个城市作为中转联运枢纽城市,进行货物的集散、中转活动,以实现低成本、高效率、低污染的联合运输。
货源城市的发货量、公路货运距离、铁路货运距离、公路运输速度、铁路运输速度影响货运运输总成本、总时间、路径上温室气体排放量。各货源城市的发货量采用模拟数据,货源城市的公路和铁路货运总量乘以该城市的出口贸易依存度作为发货量(如表 1所示)。铁路货运距离依据《货物运价里程表》整理后得到,其中,部分城市有多个货运站则使用统一货运站,城市间有多条路径的选择最短路径。公路货运起始点与铁路货运起始点相同,通过百度地图测量的两地之间最短距离作为公路货运距离。公路运输速度取货运路线的最高限速和最低限速的平均值。铁路运输速度=铁路货运距离/(运行时间+中转时间),其中运行时间为城市间最长运行时间,来源于中铁客户服务中心,中转时间来源于国家统计局。其他参数如表 2所示。公路的车辆和技术参数来源于《道路运输车辆燃料消耗量达标车型》和《2015年交通运输行业发展统计公报》,铁路的技术参数来源于《2015年铁道统计公报》,表 2中的不确定参数采用随机数。
| 编号 | 城市 | 发货量/万t |
| 1 | 重庆 | 22 708.46 |
| 2 | 成都 | 9 559.75 |
| 3 | 贵阳 | 5 094.49 |
| 4 | 昆明 | 13 426.48 |
| 5 | 西安 | 11 741.04 |
| 6 | 兰州 | 1 557.67 |
| 7 | 西宁 | 572.37 |
| 8 | 银川 | 3 127.46 |
| 注:数据来源根据9个城市的公路和铁路发货总量和货源节点城市的出口贸易依存度模拟得到,即货源城市发货量=各市公铁发货总量×各市出口贸易依存度。 | ||
| 参数 | 取值 |
| m | 8 |
| cr | (860, 1 380) |
| tdd | (1.5, 2.5) |
| α | (0, 1) |
| δ | 0.432 |
| μk | 1/10 |
| n | 16 |
| cd | (2 850, 4 210) |
| LW | 27.49 |
| β | (0, 1) |
| λk | 1/15 |
| RWk | (132 000, 180 000) |
| tdr | (1.5, 2.5) |
| trr | (5.5, 7.5) |
| M | 30.48 |
| γ | 0.027 2 |
| ck | 2 |
| 注:数据来源为《2015年交通运输行业发展统计公报》和《2015年铁道统计公报》。货车的参数指标使用40 ft普通集装箱卡车的参数。 | |
3.2 算例求解
运用MATLAB实现模拟退火算法,设置初始温度t0=0.1633,温度下降策略tk+1=0.9tk,内循环次数NL=50,外循环次数L=200,MATLAB实现程序的伪代码如下所示:
1 simulated annealing (){
2 weight←w; delivering←D; hrdistance←d; distance←d0; maxrun←L; maxrunN←NL; hrvelocity←v; velocity←v0
3 temperature=0.1633; bat=0.9; m=8;n=16;
4 a←rand(m)>0.5
5 for(i=1:m){
6 for(j=1:m){
7 if (i= =j){
8 a(i, j)= a(i, j);
9 else
10 a(i, j)=a(j, i);
11 }
12 }
13 }
14 a0←a(m+1, :); k←floor(1+n*rand()); X←zeros(1, n);
15 X(k)=1;
16 Z0=funpingjia_Z(d, d0, v, v0, a, a0, D, X, w);
17 best_X←X; best_a←a; best_a0←a(m+1, :); best_Z←Z0;
18 l←0
19 while (l < maxrun){
20 nl=0;
21 while (nl < maxrunN){
22 X←rand_X(best_X, n); a←rand_aZ(best_a, m); a0←a(m+1, :);
23 Z0=funpingjia_Z(d, d0, v, v0, a, a0, D, X, w);
24 delta_e=E-best_E
25 if (delta_e < 0){
26 best_X←X; best_a←a; best_a0←a(m+1, :); best_Z←Z0;
27 else if(exp(-delta_e/temperature)>rand())
28 best_X←X; best_a←a; best_a0←a(m+1, :); best_Z←Z0;
29 }
30 nl++;
31 }
32 temperature= bat*temperature;
33 l++
34 }
35 }
总成本、总时间、路径上温室气体排放量、枢纽上温室气体排放量在目标函数中所占权重w取值不同的情况下,MATLAB的运行结果如下:
(1) 当w=(1, 0, 0, 0) 时,即目标函数为成本最小化的单一目标函数时,最优解为X6=1或X14=1,枢纽与货源城市、目的地之间的最佳运输方式均为铁路运输。这说明当只考虑城市间的运输成本时,铁路运输方式明显优于公路运输方式。
(2) 当w=(0, 1, 0, 0) 时,即目标函数为总时间最小化的单一目标函数时,最优解为X6=1或X14=1,枢纽与货源城市之间的最佳运输方式均为公路运输,枢纽与目的地之间的最佳运输方式为铁路运输。这说明当只考虑城市间的运输时间时,公路运输方式明显优于铁路运输方式,而由于枢纽与目的地之间开通了铁路直达货运班列,使得枢纽与目的地之间的铁路运输方式优于公路运输方式。
(3) 当w=(0, 0, 1, 0) 时,即目标函数为路径上温室气体排放量最小化的单一目标函数,最优解为X6=1或X14=1,枢纽与货源城市、目的地之间的最佳运输方式均为铁路。这说明只考虑运输过程中的温室气体排放量时,铁路运输方式明显优于公路运输方式。
(4) 当w=(0, 0, 0, 1) 时,即目标函数为枢纽上温室气体排放量最小化的单一目标函数。由式(10) 可知,当枢纽为铁路枢纽时,枢纽上的温室气体排放量为0;当枢纽为公路枢纽时,枢纽上的温室气体排放量与城市交通全天拥堵延迟指数成正比,即在城市交通全天拥堵指数小的城市建设枢纽。此时,该问题存在多个最优解,即在任意城市建设铁路枢纽均为最优解。
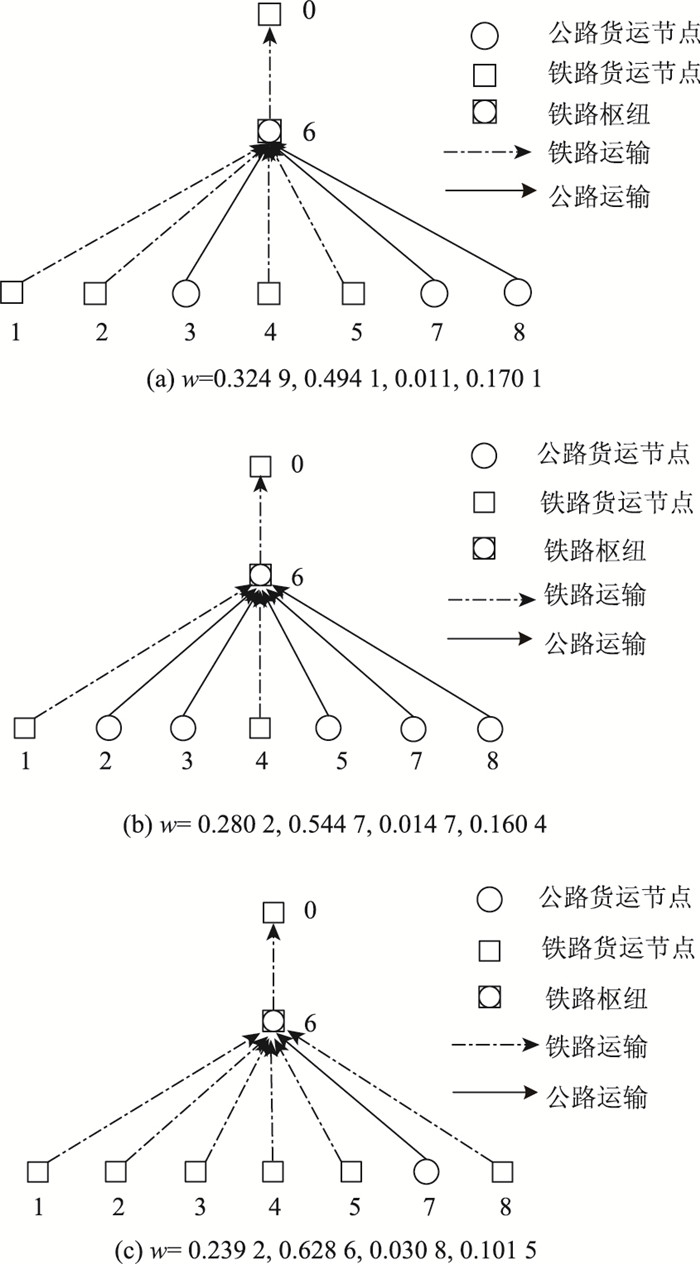
(5) 当w=(0.324 9, 0.494 1, 0.011, 0.170 1) 时,计算得到最优解为X14=1,货运城市与枢纽、目的地之间的最佳运输方式如图 3(a)所示。
|
| 图 3 货源城市、枢纽与目的地的关系 Fig. 3 Relationships among commodity source city, hub and destination |
| |
(6) 当w=(0.280 2, 0.544 7, 0.014 7, 0.160 4) 时,最优解为X14=1,货源城市、枢纽和目的地之间的运输方式如图 3(b)所示。
(7) 当w=(0.239 2, 0.628 6, 0.030 8, 0.101 5) 时,最优解为X14=1,货源城市、枢纽和目的地之间的运输方式如图 3(c)所示。
由以上(1)~(3) 的3种极端情况可知,成本、时间和温室气体排放量在总目标函数中所占权重直接影响货源城市、枢纽和目的地之间运输方式的选择,但不直接影响枢纽城市的选择。第(4) 种情况下,由于不考虑铁路枢纽的温室气体排放量,因此,最优解为任意城市的铁路枢纽。第(5)~(7)3种情况表明,随着w取值的变化,联运枢纽位置不变,但联运枢纽与货源城市之间的运输方式发生变化。
3.3 算法有效性检验以上结果是在运输方式不确定的情况下,通过城市间运输方式和枢纽位置的同时变化来搜索枢纽位置和最佳运输方式。为验证模型和算法的有效性,先确定城市间最佳运输方式,然后通过枢纽位置的变化,搜索最佳的枢纽位置。
以成本、时间和路径上温室气体排放量综合最小化为目标,确定城市间的最佳运输方式。a=(aij)(m+1)×m为(m+1)×m的0-1矩阵,其中aij(i, j=1, 2, …, m)为城市i与j之间采用的运输方式,aj, 0=am+1, j(j=1, 2, …, m)为城市j到目的地采用的运输方式。成本、时间和路径上温室气体排放量函数分别如式(21)~(23) 所示,综合目标函数如式(24) 所示。

|
(21) |

|
(22) |
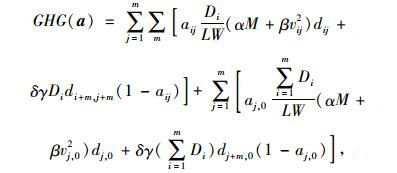
|
(23) |
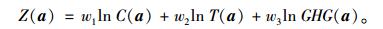
|
(24) |
式中,w=(w1, w2, w3)为成本、时间和路径上温室气体排放量在优化中所占权重,为便于与上面第(5) 种情况比较,取w=(0.324 9, 0.494 1, 0.011, 0.170 1),运用模拟退火算法进行求解,得到最佳的运输方式矩阵a*,如(25) 所示,其中,1表示公路运输,0表示铁路运输,第1~8行表示8个货源城市间的最佳运输方式,第9行为各城市到目的地的运输方式。

|
(25) |
将最佳运输方式矩阵代入式(13)~(16),得到关于枢纽选址变量X的4个目标函数,应用MATLAB实现枚举法,从16个解中选择最优解为:X14=1。由此可知,模型运用模拟退火算法求解得到的解为最优解X14=1,且最佳运输方式如图 3所示。
4 结论本研究针对国际通道中转枢纽的配置问题,综合考虑运输成本、运输效率和环境影响等因素,选择最佳联运中转枢纽,并协调多种运输方式,实现了国际通道的可持续发展。以货物运输全过程的成本、时间和温室气体排放为目标函数,中转枢纽选址变量和运输方式选择变量为决策变量,构建了可持续联运枢纽配置模型。将模型应用于西部通道中转枢纽的设计中,运用MATLAB平台设计模拟退火算法进行求解,得出成本、时间和温室气体排放量所占权重不同的情况下的最优解及最佳运输方式配置。模型的应用可以进一步推广到国际通道的中转枢纽布局中,决策者通过调节成本、时间和温室气体排放量在目标函数中所占权重,确定枢纽位置和最佳运输方式配置。
| [1] | 董千里, 杨磊, 常向华. 基于国际中转枢纽港战略理论的中欧班列集成运作研究[J]. 科技管理研究, 2016, 36(22): 230-236 DONG Qian-li, YANG Lei, CHANG Xiang-hua. Research on China-Europe Trains Integrated Operations Based on International Transit Hub Port Strategy Theory[J]. Science and Technology Management Research, 2016, 36(22): 230-236 |
| [2] | 张琦. 内陆中转型铁路枢纽集装箱海铁联合运输组织理论研究[D]. 北京: 北京交通大学, 2011. ZHANG Qi. Theoretical Research on Sea-rail Combined Transport Organization of the Inland-port-transferring Railway Hub Container Transport System[D]. Beijing:Beijing Jiaotong University, 2011. |
| [3] | 陈沿伊. 基于运网要素互动的综合货运枢纽布局理论与方法研究[D]. 武汉: 武汉理工大学, 2012. CHEN Yan-yi. Theory and Methods of Layout of Integrated Freight Hub Based on Interaction of Transport Network Elements[D].Wuhan:Wuhan University of Technology, 2012. https://wuxizazhi.cnki.net/lunwen-1013134729.html |
| [4] | 王清斌, 靳志宏, 张爽, 等. 内陆集装箱多式联运枢纽配置[J]. 大连海事大学学报, 2013, 39(3): 91-94 WANG Qing-bin, JIN Zhi-hong, ZHANG Shuang, et al. Multimodal Transport Hub Configuration of Inland Container[J]. Journal of Dalian Maritime University, 2013, 39(3): 91-94 |
| [5] | 尹莉. 联运物流网络的货运枢纽选址研究[D]. 成都: 西南交通大学, 2013. YIN Li. Study on Location of Freight Hubs in Intermodal Transportation Network[D]. Chengdu:Southwest Jiaotong University, 2013. https://wuxizazhi.cnki.net/lunwen-1013248225.html |
| [6] | 贺政纲, 邹晔, 杨晓. 报废汽车物流网络选址-路径问题建模与求解算法研究[J]. 公路交通科技, 2016, 33(3): 138-145 HE Zheng-gang, ZOU Ye, YANG Xiao. Research of Modeling and Algorithm for ELV Logistics Network Location-routing Problem[J]. Journal of Highway and Transportation Research and Development, 2016, 33(3): 138-145 |
| [7] | 王勇, 张永, 毛海军, 等. 基于改进蚁群算法的多物流中转站选址规划[J]. 公路交通科技, 2011, 28(8): 140-146 WANG Yong, ZHANG Yong, MAO Hai-jun, et al. Multi-logistics Transfer Stations Allocation Based on Improved Ant Colony Optimization Algorithm[J]. Journal of Highway and Transportation Research and Development, 2011, 28(8): 140-146 |
| [8] | FARAHANI R Z, HEKMATFAR M, ARABANI A B, et al. Hub Location Problems:A Review of Models, Classification, Solution Techniques, and Applications[J]. Computers & Industrial Engineering, 2013, 64(4): 1096-1109 |
| [9] | MOHAMMADI M, TORABI S A, TAVAKKOLI-MOGHADDAM R. Sustainable Hub Location under Mixed Uncertainty[J]. Transportation Research Part E:Logistics & Transportation Review, 2014, 62: 89-115 |
| [10] | LAM S L, GU Y. A Market-oriented Approach for Intermodal Network Optimisation Meeting Cost, Time and Environmental Requirements[J]. International Journal of Production Economics, 2016, 171(2): 266-274 |
| [11] | ALUMUR S A, KARA B Y, KARASAN O E. Multimodal Hub Location and Hub Network design[J]. Omega, 2012, 40(6): 927-939 |
| [12] | BARTH M, BORIBOONSOMSIN K. Energy and Emissions Impacts of a Freeway-based Dynamic Eco-driving System[J]. Transportation Research Part D:Transport & Environment, 2009, 14(6): 400-410 |
| [13] | PETERSON M D, BERTSIMAS D J, ODONI A R. Models and Algorithms for Transient Queueing Congestion at a Hub Airport[J]. Management Science, 1995, 41(8): 1279-1295 |
| [14] | MARIANOV V, SERRA D. Location Models for Airline Hubs Behaving as M/D/c Queues[J]. Computers & Operations Research, 2000, 30(7): 983-1003 |
| [15] | MOHAMMADI M, JOLAI F, ROSTAMI H. An M/M/c Queue Model for Hub Covering Location Problem[J]. Mathematical & Computer Modelling, 2011, 54(11/12): 2623-2638 |
| [16] | 李士勇. 智能优化算法原理与应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2012. LI Shi-yong. Intelligent Optimization Algorithm Theory and Applications[M]. Harbin: Harbin Institute of Technology Press, 2012. |
| [17] | MOUSAVI S M, TAVAKKOLI-MOGHADDAM R. A Hybrid Simulated Annealing Algorithm for Location and Routing Scheduling Problems with Cross-docking in the Supply Chain[J]. Journal of Manufacturing Systems, 2013, 32(2): 335-347 |
| [18] | ZHAN SH, LIN J, ZHANG Z J, et al. List-based Simulated Annealing Algorithm for Traveling Salesman Problem[J]. Computational Intelligence & Neuroscience, 2016(5): 1-12 |
| [19] | CHEN S M, SAROSH A, DONG Y F. Simulated Annealing Based Artificial Bee Colony Algorithm for Global Numerical Optimization[J]. Applied Mathematics & Computation, 2012, 219(8): 3575-3589 |
 2017, Vol. 34
2017, Vol. 34
