扩展功能
文章信息
- 李明燏, 梁丽萍, 鲁燕霞
- LI Ming-yu, LIANG Li-ping, LU Yan-xia
- 基于改进禁忌搜索算法的车辆路径问题模型
- A Model of Vehicle Routing Problem Based on Improved Tabu Search Algorithm
- 公路交通科技, 2017, 34(10): 108-114
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(10): 108-114
- 10.3969/j.issn.1002-0268.2017.10.015
-
文章历史
- 收稿日期: 2017-02-22
随着市场经济的发展,能源以及成本问题日益成为制约企业发展的重要问题,物流作为企业的“第三利润源”的作用也逐渐显现出来。物流是供应链的重要组成部分,合理地使用各项运输工具,优化运输路线,降低物流成本是物流管理的重要内容。在组成物流成本的各项费用中,运输成本占了重要的比例,而车辆路径问题则是运输系统的核心问题,运用各种算法,对路径进行优化,可以实现物流的合理化,因此本研究所做的研究具有重要的理论与现实意义。
1 车辆路径问题的研究综述1959年Dantzig和Ramse对闭合式VRP首次进行了研究,并且给出了相应的数学模型和算法,1964年Clark和Wright改进了Dantzig和Ramse的算法,这两位学者的研究使得VRP问题成为运筹学的热门话题,随后VRP问题的研究取得不少的成果。对于车辆路径问题的研究方法可以分为3大类:精确算法、经典启发式算法和现代启发式算法。精确算法主要包括分枝定界法、割平面法、动态规划法等,用于求解小规模的最优解问题;经典启发式算法主要包括Clarke和Wright提出的C-W节约算法[1]、Gillett和Miller提出的扫描算法[2],以及Solomon提出的最近邻启发式算法[3],另外还有k-opt以及K-interchange算法[4];现代启发式算法包括禁忌搜索、模拟退火、蚁群算法等,近年来随着计算机技术的发展,现代启发式算法得到了更加广泛的应用。
VRP问题研究在中国兴起以来,我国学者对其进行了诸多探索。袁建清建立了求解动态车辆调度问题的混合禁忌搜索算法[5];潘立军对带时间窗的车辆路径问题及其算法进行了总结[6];温惠英对基于自适应离散粒子群算法的带时间窗协同车辆路径问题进行了总结研究[7];杨海宁对基于元启发式算法的复杂车辆路径问题进行了总结研究[8]。与国外的相关文献研究相比,我国对于VRP问题的研究还处于起步阶段。
在国外的研究中,许多VRP问题类型都考虑了异构车队的问题,比如车辆有各种容量、固定成本、变动成本、每种类型车辆的数量,或者车辆返回到仓库的最迟时间限制等。
在异构车队的车辆路径问题(VRPHE)中,不同的车辆类型有不同的运载能力,车辆的数量没有限制。异构车队的车辆路径问题(VRPHE)解决方案是要找到一个车队和相应路线计划,从而使总成本最小化。异构车队的车辆路径问题(VRPHE)产生于战略决策,比如一个公司要构建一个车队的时候,用这种方法来确定车队的规模大小以及组成情况。
固定成本的异构车队车辆路径问题(VRPHE-F)只考虑了总成本中的固定成本,它是由Golden, Assad,Levy, 及Gheysens在1984年提出的[9]。Taillard在1999年开发了一种基于禁忌搜索的启发式列生成方法,对基于可变成本的异构车队车辆路径问题(VRPHE-V)构造了8个测试问题,运用列生成算法来运行了该模型[10]。Renaud和Boctor分析了启发式方法,改进了固定成本的异构车队车辆路径问题(VRPHE-F)的程序[11]。Choi和Tcha提出了一种基于列生成的bond算法,他们对基于固定成本的异构车队车辆路径问题和基于变动成本的异构车队车辆路径问题(VRPHE-F和VRPHE-V)进行了测试,并得出结果, 也解决了带有固定和可变成本的异构车队车辆路径问题(VRPHE-FV)[12]。Prins在2009年介绍了带有遗传算法和本地搜索的杂交算法来解决VRPHE[13]。Brandao在2011年设计了禁忌搜索算法并引入了一些新的测试问题[14]。
带有时间窗和异构车队的车辆路径问题是由Liu和Shen在1999年首先提出的,他们在Golden等工作的基础上开发了一个节约型构造启发式算法和改进启发式算法[15]。随后,Dullaert, Janssens, Sorensen, 及Vernimmen在2002年提出新的启发式算法,比之前的启发式方法更好地解决这一问题[16]。Belfiore和Favero在2007年提出通过分散搜索来解决VRPHETW[17]。Dell’Amico等在2007年提出了一个基于并行算法的高效的解决方案[18]。Paraskevo-poulos, Repoussis, Tarantilis, Ioannou, 及Prastacos在2008年提出了一个基于杂交启发式算法的带有一个新的反应变量的两阶段解决方案[19]。陶胤强等建立了带时间窗的多车型多费用车辆路径问题的模型和算法[20]。
现有文献对于带有时间窗和异构车队的车辆路径问题的研究,远少于带有时间窗的车辆路径问题的研究。Rochat和Semet在1994年提出了对于VRPTW的禁忌搜索方法,考虑到司机的休息时间和访问性的限制[21]。Yepes and Medina在2006年提出了基于概率变量的三步本地搜索算法[22]。除了对于VRPHETW的研究较少以外,大部分文献对于VRPHETW的研究集中在实际的应用方面,因此,测试问题和结果不具有可比性。表 1总结了不同文献在研究方面的侧重点以及约束条件。
| 问题变体 | 引用文献 | 固定成本 | 变动成本 | 车辆数限制 | 时间窗 |
| FSMVRP-FV | Choi and Tcha (2007), Prins (2009) | √ | √ | ||
| FSMVRP-V | Taillard (1999), Gendreau et al. (1999) | √ | |||
| FSMVRP-F | Golden,et al. (1984), Taillard (1999) | √ | |||
| VRPHE | Prins (2009), Brandão (2011) | √ | √ | ||
| FSMVRPTW | Kritikos and Ioannou(2013) | √ | √ |
对于文献的梳理可以发现,现有研究一般假设车辆的数量是没有限制的,求解在满足一定约束的情况下,使旅行路线最短或者使用的车辆数最少。然而在车辆路径问题的实际应用中,可能会面临着许多资源约束条件,比如车辆数量有限,车型也是不同的。面对这一现实问题,本研究提出了带有时间窗、异构车队以及车辆数量有限的车辆路径问题。
2 VRPHETW问题描述与建模 2.1 问题描述带有时间窗和异构车队的车辆路径问题(VRPHETW)可以描述为:从某物流中心出发,用多辆配送车向多个用户点进行配送,每个用户点的位置和需求量一定,将货物送达的时间窗也是一定的,配送车有多种类型,每种类型的载重量不同,并且车辆数是有限的。要求每辆车从配送中心出发,经过一系列的用户点之后回到配送中心,规定每个用户点只能有一辆车来配送,且不能超过车辆的最大容量,求以最大服务用户点以及最小成本为目标的车辆行驶路线。
将上述问题描述转化为数学问题:给定一个完全图G(V, A),其中V=(0,1,2, …, n)为图的顶点集,A={(i, j): i≥0, j≤n, i≠j}为弧集。顶点0表示配送中心,顶点N={1,2,…, n}, A代表两个顶点之间的联系,tij则表示每条弧(i, j)的旅行时间或距离。
定义一些数学符号如下:
di:每个用户点i(i∈N)的固定的需求量,其中d0=0;
[ei, lj]:用户点i的服务时间窗,代表用户点允许的最早和最迟服务时刻,时间窗是与顶点相关联的,如[e0, l0]=[E, L],E和L分别代表离开顶点的最早时间和返回顶点的最迟时间
si:在用户点i的服务时间,其中s0=0;
C:车辆类型集,{1,2,3, …, c};
sc:c类型车辆数;
K:车辆数集合,{1,2,3, …, k};
qc:类型为c的车辆的装载能力;
fc:使用一辆类型为c的车辆固定费用;
αc:类型为c的车辆的单位行驶费用。
模型中的决策变量为:
xijk:若车辆k经过了弧(i, j),则等于1,否则为0;
aik:车辆k到达用户点i的时间;
wik:车辆k在用户点i的等待时间。
2.2 模型建立VRPHETW的数学模型可以表示为:
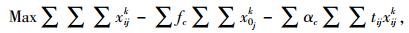
|
(1) |
约束:
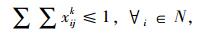
|
(2) |
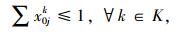
|
(3) |
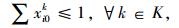
|
(4) |
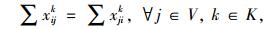
|
(5) |
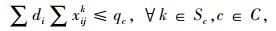
|
(6) |
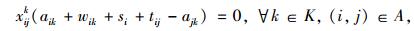
|
(7) |
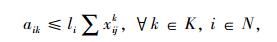
|
(8) |
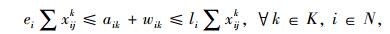
|
(9) |
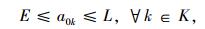
|
(10) |
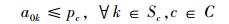
|
(11) |
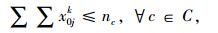
|
(12) |
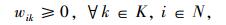
|
(13) |
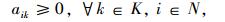
|
(14) |
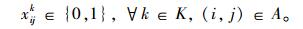
|
(15) |
带有时间窗和异构车队的车辆路径问题(VRPHETW)的约束条件是一个层次目标函数,客户访问数量被认为是一级约束目标, 使拜访的客户量达到最大化,二级约束目标是车辆成本,包括固定成本和变动成本。目标函数(1) 中的△i+表示一组来自弧集(i, j)∈A的顶点j的集合,sc代表车辆类型c的集合。约束条件(2) 表示任一个用户点都只被一辆车服务。约束条件(3)~(5) 防止车辆多次指派。约束条件(6) 能力约束,表示对于任一车辆所服务的路线上的用户点的需求量之和不大于车辆的装载能力。约束条件(7) 表示车辆在服务完上一个用户点之后,即服务下一个用户点,中间没有时间间隔。约束条件(8)~(10) 是对于用户点和配送中心的时间窗约束。约束条件(11) 限制了车辆的最迟返回时间,约束条件(12) 限制了每种类型车辆的可用数量,nc为可以使用的车辆数量。约束条件(13)~(15) 限制了变量的取值范围。
3 改进禁忌搜索算法对于带有时间窗的车辆路径问题(VRPTW),现有文献中大多使用禁忌搜索算法来进行求解,但对于本研究提出的带有车辆数量限制的车辆路径问题(VRPHETW),可以从以下两方面进行考虑:(1) 使用插入法来判断该问题是不是可行,即现有车辆是否可以满足用户需求,这样的话,就可以产生2个算法集合,对于可满足需求的和不可满足需求的案例分别进行求解。(2) 增加车辆数以满足所有用户的需求,然后根据算法获得一个尽量多的服务用户点的路线方案。
然而以上2种算法都是有缺陷的,虽然第1种方案看起来更可行,但是它需要使用多种启发式算法来进行;第2种方案没有考虑车辆无法满足用户需求的情况,因此无法给出一个可行解。基于以上问题,综合以上可以满足用户需求及不能满足用户需求的情况,提出了使用保留表来解决以上问题。
3.1 保留表保留表中包含了在当前解的情况下没有被服务的用户点,添加保留表的想法是来源于运筹学中的单纯形算法,单纯形算法的第一阶段会增加人工变量,当所有的人工变量都移除后,则找到了满意解。同理,当保留表中的所有的用户点都被移除之后,也就找到了一个满意解。
同时保留表自身可以产生一个扩展的邻域结构,除了上文提到的几种构造邻域结构的基本方法之外,还包括以下几种:
(1) 从保留表中移出(Relocate from holding list):将用户点从保留表移动到现有路径上;
(2) 移动到保留表(Relocate to holding list):将用户点从现有路径移动到保留表上;
(3) 保留表上的交换(Exchange with holding list):将现有路径上的用户点与保留表中的用户点进行交换。
该保留表相当于一个虚拟的路径,所以一个用户点插入到保留表中或者从保留表中进行移除都是可以的。已选择路径上的用户点可以与保留表中的用户点进行以上提到的交换和移动。当然,对于如何决定下一步移动的方向,本研究构造了一个等级成本结构原则来进行衡量。
3.2 等级成本结构原则对于有数量限制的车辆路径问题,根据设立的目标方程,可以发现,最大可能地服务更多的顾客是本研究的第一目标,因此在禁忌搜索算法移动寻找邻域解的过程中,要遵循以下原则:
(1) 使服务的客户数量最大化;
(2) 使用的车辆数尽可能得少;
(3) 经过的旅行距离尽可能得短。
3.3 车辆排序准则对车辆进行排序一般遵循以下3项准则中的1种:最大装载能力准则;最小装载能力准则;贪婪插入准则。
本研究采用的是“最大装载能力准则”,即最大装载能力的车辆优先被选择去配送。
3.4 改进禁忌搜索算法原理为了解决车辆数量有限制的车辆路径问题,本研究提出的算法是融合了两阶段算法使之成为一个嵌套算法。在每一个迭代过程中,使用标准的禁忌搜索算法来找到可以插入的最大用户数,同时,每一个迭代过程中的车辆数是固定的,因此在迭代过程中不能考虑使用增加车辆数的方法来满足那些没有被服务的用户点,也就是说,迫使用户点在已有的路径上进行紧密排列。
由于在算法中加入了保留表,改进了原有的禁忌搜索算法,使用等级成本结构的原则使用户点从保留表向现有路径进行移动,在算法中,搜索空间总是可行的,因为保留表本身可以产生邻域结构。
3.5 算法程序首先来定义一些用于描述两阶段禁忌搜索过程的符号。集合K代表了所有的车辆,holding list包含了所有的用户点。TS表示考虑了等级成本结构的标准禁忌搜索迭代过程,禁忌列表存储着已经搜索过的局部最优点,如果用户点在禁忌列表中或者不是满足特赦准则的更优解,则该移动是被禁止的。StepSize表示在每次迭代过程中额外引入的车辆数量;numVeh表示目前所使用的车辆数;在该数量的车辆情况下,如果连续CountLimt次尝试后仍然没有找到一个更好的方案, 这个阶段结束, 算法继续下一阶段,并添加更多的车辆。
整个过程可以进行如下描述:初始禁忌表中包含了所有用户点,StepSize表示在每次迭代过程中额外引入的车辆数量。每一个迭代过程是从While开始的一个循环,也就是从步骤(3) 到步骤(6)。在步骤(4) 中引入了TS,也就是上文提到的考虑了等级成本结构的标准禁忌搜索迭代过程,经过步骤(4),将返回一个经过迭代过程的解决方案,该方案是与原有方案不同的。在步骤(5),一个更好的解决方案是指在满足了等级成本结构原则下,该方案比原来的解决方案更优。如果经过CountLimit尝试后,仍然没有发现更好的解决方案,则该迭代过程结束,通过增加车辆来进入下一阶段。伪代码如下:
Until [H]=0 or numVeh=[K] (1)
Set count=0 (2)
While count < =CountLimit (3)
Call TS based on numVeh Vehicles; (4)
If better solution found (5)
Set count=0;
Else
Set count =count+1;
EndWhile; (6)
Set numVeh=min(numVeh+StepSize, [K]) (7)
End until; (8)
4 案例分析 4.1 测试数据为检验算法的准确性,本研究使用具体的案例来进行操作。有1个配送中心,15个用户点,配送点及各用户中心的坐标、需求量及配送时间窗如下表 1所示,表 1中0表示配送中心。有3种类型的车辆,各车辆的载货量、行驶速度以及固定费用、单位行驶费用如下表 2所示。
| 编号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| X | 26 | 19 | 33 | 73 | 49 | 70 | 27 | 10 | 39 | 16 | 68 | 10 | 83 | 88 | 32 | 70 |
| Y | 30 | 0 | 3 | 85 | 73 | 94 | 44 | 69 | 25 | 81 | 76 | 57 | 43 | 52 | 58 | 18 |
| D | 0 | 1 | 1.8 | 1.1 | 0.6 | 1.9 | 1.4 | 1.2 | 0.2 | 1.7 | 0.8 | 0.9 | 0.8 | 1.9 | 1.6 | 0.9 |
| ET | 74 | 58 | 15 | 46 | 47 | 85 | 21 | 59 | 37 | 21 | 74 | 58 | 15 | 56 | 87 | |
| LT | 144 | 128 | 85 | 106 | 117 | 155 | 91 | 119 | 107 | 121 | 174 | 158 | 125 | 156 | 187 |
| 车型 | 行驶速度 | 拥有数量 | 固定成本 | 单位行驶费用 |
| A | 2 | 1 | 200 | 2 |
| B | 1.5 | 1 | 150 | 1.5 |
| C | 1 | 2 | 100 | 1 |
4.2 演算过程
根据所构建的算法,首先禁忌表为空,保留表中包含了所有的用户点,H为15;车辆数K为4;设CountLimit为50,即在该数量的车辆下,允许迭代的最大次数。在TS中,设禁忌长度为3。本研究使用成熟的软件进行直接操作,若感兴趣,可以在C++上进行编程运算。
选取其中的某一次迭代为例,进行算法的具体演示,具体算法过程如下:
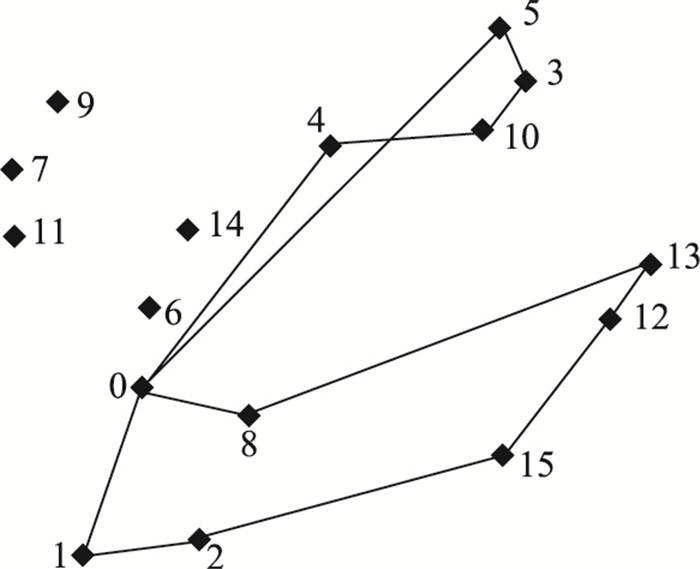
设numVeh为2,即当前拥有的车辆数,根据最大装载能力原则,该2辆车分别为A和B两种类型。选取其中一条运输路径为:0-4-10-3-5-0-1-2-15-12-13-8-0, 其中用户点6,7,9,11,14没有被配送,仍然在保留表中,路线如图 1所示。
|
| 图 1 两辆车服务10个用户点的路线图 Fig. 1 Route of 2 vehicles serving 10 customer points |
| |
此时有10个用户点被服务,总路径长度为358.846。进行一次TS迭代,按照等级成本结构的3个原则,(1) 各车的装载量分别为4.4和6.6,而剩余为配送用户点最少需求量为0.9,所以无法增加用户点;(2) 车辆数为2,满足最少车辆原则;(3) 下一步迭代的方向为路径最短。
采用交换法产生邻域结构的方法,将用户点5和10进行交换,同时采用插入法产生邻域结构的方法,将用户点8插入另一条路径中,产生路径0-4-5-3-10-8-0-1-2-15-12-13-0,路线如图 2所示。
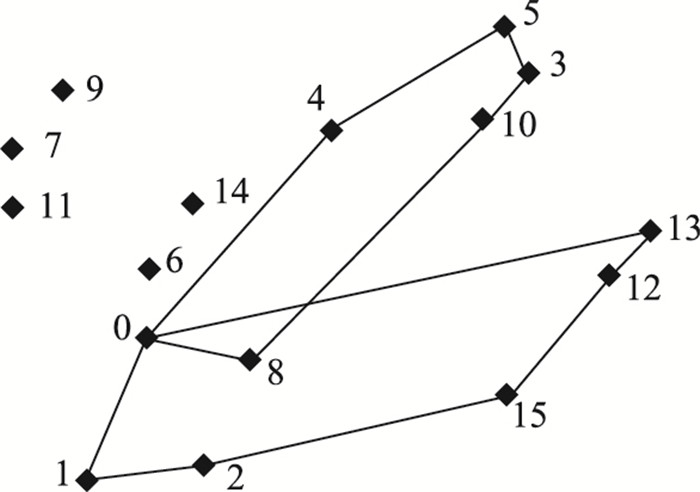
|
| 图 2 经过一次TS迭代后的路线图 Fig. 2 Route after a TS iteration |
| |
此时有10个用户点被服务,总路径长度为360.153。由于路径长度多于原来一条路径,因此没有找到更优解,count=count+1,若count < =countLimit,即小于50,则继续迭代,否则结束。此时假设其小于50。同上,按照等级成本结构的3个原则,(1) 各车的装载量分别为4.6和6.4,而剩余未配送用户点最少需求量为0.9,所以无法增加用户点;(2) 车辆数为2,满足最少车辆原则; (3) 下一步迭代的方向为路径最短。
采用插入法产生邻域结构的方法,将用户点8插入另一条路径中,产生路径0-4-5-3-10-0-1-2-15-12-13-8-0,用户点6,7,9,11,14仍然没有被配送,路线如图 3所示。
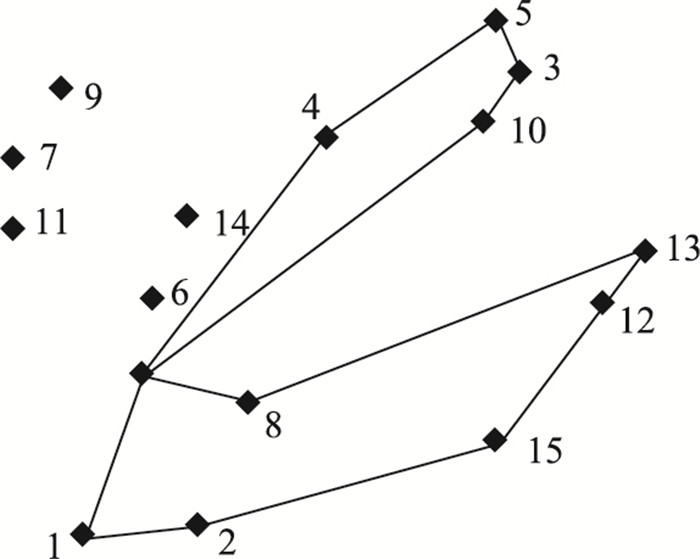
|
| 图 3 经过两次TS迭代后的路线图 Fig. 3 Route after 2 TS iterations |
| |
此时有10个用户点被服务,总路径长度为353.933。由于路径长度少于原来一条路径,因此找到一个更优解。将该解与禁忌表中的解进行比较,若满足特赦原则,则将禁忌表中解禁忌,同时将该解放入禁忌表中,若不满足禁忌准则,则用该解代替原来的解成为当前解。此时找到一个更优解,因此设count=0,在此产生邻域结构进行迭代。最后搜索的结果如图 4所示。
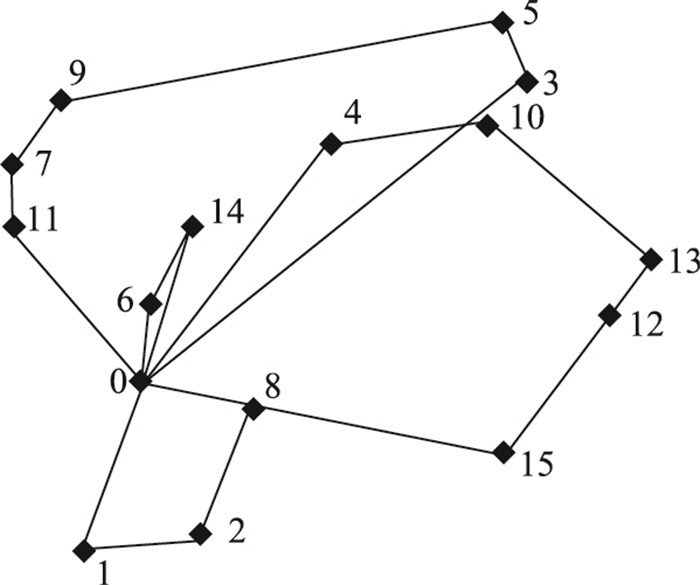
|
| 图 4 经过多次迭代最终输出的路线图 Fig. 4 Final route after multiple iterations |
| |
A车配送路线为:0-3-5-9-7-11-0;B车配送路线为:0-4-10-13-12-15-0;C1车配送路线为:0-6-14-0;C2车配送路线为:0-1-2-8-0。总配送路程为:516.982,运输成本为4辆车的固定成本与运输成本之和:6 302.923。
由于篇幅有限,无法展示所有的迭代过程,图 4给出的结果是在具体的软件上操作的最终结果。
5 结论本研究在带有时间窗的车辆路径问题的基础上,提出了带有车辆数量限制的车辆路径问题,介绍了改进禁忌搜索算法的原理,在原有禁忌搜索算法的基础上对其进行了创新,在原算法中加入了保留表,车辆排序准则改进了原有的禁忌搜索算法,使用等级成本结构的原则,使用户点从保留表向现有路径进行移动,在算法中,搜索空间总是可行的,因为保留表本身可以产生邻域结构,改进的禁忌搜索算法,形成了一个嵌套式的结构,既方便了算法的运行,又可以促进各个用户点在路径上的紧密排列,从而达到优化运输路线的目的。改进的禁忌搜索算法解决了传统禁忌搜索算法程序复杂、独立性低下等弊端,最后为了验证改进的禁忌搜索算法的有效性,使用具体的案例对于改进的禁忌搜索算法进行了验算,尤其是对于其迭代过程进行详细的描述,最后证明了该算法是有效的。
| [1] | CLARKE G, WRIGHT J W. Scheduling of Vehicles from a Central Depot to a Number of Delivery Points[J]. Operations Research, 1964, 12(4): 568-581 |
| [2] | GILLETT B E, MILLER L R. A Heuristic Algorithm for the Vehicle-dispatch Problem[J]. Operations Research, 1974, 22(2): 340-349 |
| [3] | SOLOMON M M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constrains[J]. Operations Research, 2010, 35(35): 254-266 |
| [4] | 孙丽君, 胡祥培, 王征. 车辆路径规划问题及其求解方法研究进展[J]. 系统工程, 2006, 24(11): 31-37 SUN Li-jun, HU Xiang-pei, WANG Zheng. Reviews on Vehicle Routing Problem and Its Solution Methods[J]. Systems Engineering, 2006, 24(11): 31-37 |
| [5] | 袁建清. 求解动态车辆调度问题的混合禁忌搜索算[J]. 计算机应用与软件, 2012, 29(4): 148-150 YUAN Jian-qing. Hybrid Tabu Search Algorithm for SoLVing Dynamic Vehicle Scheduling[J]. Computer Applications and Software, 2012, 29(4): 148-150 |
| [6] | 潘立军. 带时间窗车辆路径问题及其算法研究[D]. 长沙: 中南大学, 2012 PAN Li-jun. Vehicle Routing Problem with Time Windows and Its Algorithms[D].Changsha:Central South University, 2012. |
| [7] | 温惠英, 孙博. 基于离散粒子群算法的协同车辆路径问题[J]. 公路交通科技, 2011, 28(1): 149-153 WEN Hui-ying, SUN Bo. ResoLVing Collaborative Vehicle Route Problem Based on Discrete Particle Swarm Optimization[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1): 149-153 |
| [8] | 杨海宁. 基于元启发式算法的复杂车辆路径问题研究[J]. 物流技术, 2013, 32(21): 174-176 YANG Hai-ning. Study on Complex VRP Based on Meta-heuristics[J]. Logistics Technology, 2013, 32(21): 174-176 |
| [9] | GOLDEN B, ASSAD A, LEVY L, et al. The Fleet Size and Mix Vehicle Routing Problem[J]. Computers and Operations Research, 1984, 11(1): 49-66 |
| [10] | TAILLARD E. A Heuristic Column Generation Method for the Heterogeneous Fleet VRP[J]. RAIRO Operations Research, 1999, 33(1): 1-14 |
| [11] | RENAUD J, BOCTOR F F. A Sweep-based Algorithm for the Fleet Size and Mix Vehicle Routing Problem[J]. European Journal of Operational Research, 2002, 140(3): 618-628 |
| [12] | CHOI E, TCHA D W. A Column Generation Approach to the Heterogeneous Fleet Vehicle Routing Problem[J]. Computers and Operations Research, 2007, 34(7): 2080-2095 |
| [13] | PRINS C. Two Memetic Algorithms for Heterogeneous Fleet Vehicle Routing Problems[J]. Engineering Applications of Artificial Intelligence, 2009, 22(6): 916-928 |
| [14] | BRANDAO J. A Tabu Search Algorithm for the Heterogeneous Fixed Fleet Vehicle Routing Problem[J]. Computers and Operations Research, 2011, 38(1): 140-151 |
| [15] | LIU F H, SHEN S Y. The Fleet Size and Mix Vehicle Routing Problem with Time Windows[J]. Journal of the Operational Research Society, 1999, 50(7): 721-732 |
| [16] | DULLAERT W, JANSSENS G K, SÖRENSEN K, et al. New Heuristics for the Fleet Size and Mix Vehicle Routing Problem with Time Windows[J]. Journal of the Operational Research Society, 2002, 53(11): 1232-1238 |
| [17] | BELFIORE P P, FAVERO L P L. Scatter Search for the Fleet Size and Mix Vehicle Routing Problem with Time Windows[J]. Central European Journal of Operations Research, 2007, 15(4): 351-368 |
| [18] | DELL'AMICO M, MONACI M, PAGANI C, et al. Heuristic Approaches for the Fleet Size and Mix Vehicle Routing Problem with Time Windows[J]. Transportation Science, 2007, 41(4): 516-526 |
| [19] | PARASKEVOPOULOS D C, REPOUSSIS P P, TARANTILIS C D, et al. A Reactive Variable Neighborhood Tabu Search for the Heterogeneous Fleet Vehicle Routing Problem with Time Windows[J]. Journal of Heuristics, 2008, 14(5): 425-455 |
| [20] | 陶胤强, 牛慧民. 带时间窗的多车型多费用车辆路径问题的模型和算法[J]. 交通运输系统工程与信息, 2008, 8(1): 113-117 TAO Yin-qiang, NIU Hui-min. Model and Heuristic Algorithim for the Multi-type Vehicles Routing Problem with Multiple Costs and Time Windows Limits[J]. Journal of Transportation Systems Engineering and Information Technology, 2008, 8(1): 113-117 |
| [21] | ROCHAT Y, SEMET F. A Tabu Search Approach for Delivering Pet Food and Flour in Switzerland[J]. Journal of the Operational Research Society, 1994, 45(11): 1233-1246 |
| [22] | YEPES V, MEDINA J. Economic Heuristic Optimization for Heterogeneous Fleet VRPHESTW[J]. Journal of Transportation Engineering, 2006, 132(4): 303-311 |
 2017, Vol. 34
2017, Vol. 34
