扩展功能
文章信息
- 安朗
- AN Lang
- 基于MCMC-CCRAA的大跨径斜拉桥施工风险预警模型
- A Construction Risk Early Warning Model of Long-span Cable-stayed Bridge Based on MCMC-CCRAA
- 公路交通科技, 2017, 34(10): 42-50
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(10): 42-50
- 10.3969/j.issn.1002-0268.2017.10.007
-
文章历史
- 收稿日期: 2016-09-07
近年来,我国桥梁安全事故层出不穷,造成了巨大的财产损失和人员伤亡,并且带来了不良的社会影响,而桥梁施工阶段安全事故在整个桥梁安全事故中占有较大的比例。大跨径斜拉桥的施工建造是一项庞大的系统工程,施工过程中的任何一项错误与疏忽都可能引起施工安全事故[1]。为有效降低施工风险,预防重特大安全事故的发生,交通运输部于2011年5月颁布了《公路桥梁和隧道工程施工安全风险评估指南》(试行),以规范全国桥梁施工风险评估工作,其中明确指出跨径大于400 m的斜拉桥应当进行施工安全风险评估工作,由此可见针对大跨径斜拉桥进行施工风险评估预警方面的研究十分重要。
常用的桥梁施工风险评估方法包括模糊综合评判法、神经网络法、风险矩阵法、基于可靠度的结构失效概率求解法、指标体系法、蒙特卡罗模拟法等[2-4]。国内针对斜拉桥施工风险评估已有一定的成果。巩春领[1]与刘育新[5]采用有限元、人工神经网络与蒙特卡洛模拟相结合的方法对斜拉桥施工风险概率进行了求解。王小飞[6]运用模糊网络结构分析法判断了斜拉桥施工风险级别。赵延龙[7]则基于贝叶斯网络对斜拉桥上部结构进行了施工风险分析。国外目前对于桥梁风险评估开展了一定程度的研究,但缺乏针对斜拉桥施工风险方面的研究[8-9]。尽管斜拉桥施工风险分析取得了一定成果,但仍存在一定的不足与局限:(1) 目前斜拉桥施工风险概率估计方法包括客观概率估计和主观概率估计两个方向,前者计算结果客观性强但解释性弱,与人们的认识存在差距,后者则易受主观因素的影响,但解释想较强,易于人接受;(2) 常用的风险聚合方法对风险概率的依赖性较强,易出现极值,不能有效反映风险聚合效应;(3) 现有成果缺乏对于大跨径斜拉桥施工风险预警模型的整体研究,研究成果实用性低。
基于贝叶斯理论的马尔可夫链蒙特卡罗(Markov Chain Monte Carlo,MCMC)算法能最大限度地利用已有信息,充分考虑各类不确定因素,兼具客观概率估计与主观概率估计的共同优势,提升了风险因素概率的求解精度。补偿竞争风险聚合算法(Compensation Competition Risk Aggregation Algorithm,CCRAA)依据模糊聚类存在聚类中心的思想,对风险集合中各风险值进行补偿,避免了聚合风险出现极值或对风险概率产生依赖。两种方法的综合运用可以充分发挥各自的优势,增强斜拉桥施工风险评判的可靠性。本研究将采用MCMC法与CCRAA法评估大跨径斜拉桥各施工阶段的风险值,构建实用的大跨径斜拉桥施工风险预警模型,确保桥梁施工安全。
1 MCMC算法MCMC算法是通过数值模拟的方法,直接从后验分布中生成参数向量的仿真样本,后续的统计推断工作完全基于这些样本开展,从而达到求解复杂后验分布高维积分的目的[10]。MCMC算法实际上是构造了一个马尔可夫链,使该马尔可夫链的不变分布变为所要求得的概率分布(即后验分布)。当模拟步数足够长时,可以认为生成的样本来自此马尔可夫链的不变分布,因此生成样本可作为所需求解概率分布的近似。在实际应用MCMC算法时,建议密度函数的构造至关重要,常用的构造方式包括Metropolis-Hastings抽样算法和Gibbs抽样算法。
1.1 贝叶斯基本理论MCMC算法是为了求解贝叶斯模型中的复杂后验分布,这里首先对贝叶斯基本理论进行简介。贝叶斯理论的核心是贝叶斯定理,其数学表达式为:
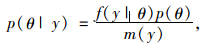
|
(1) |
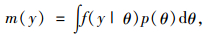
|
(2) |
式中,p(θ|y)为后验密度函数;f(y|θ)为数据的抽样密度函数;p(θ)为先验密度函数;m(y)为数据的边缘密度函数。
在贝叶斯理论中,先验分布p(θ)代表了试验前对待估参数的初始估计,每次试验结果被认为是关于待估参数的“新的信息”,利用“新的信息”对先验分布进行更新。由于更新后待估参数的概率分布反映了得到试验数据后对参数的认识,所以该分布被称为后验分布。
1.2 Gibbs抽样Metropolis-Hastings抽样算法对建议密度函数的要求过高,“过宽”或“过窄”都会影响算法的精度,具体抽样方法见文献[10],这里不再赘述。Gibbs抽样则是对参数向量中的每个元素都指定一个抽样时采用的条件分布,而不像Metropolis-Hastings抽样仅给出一个建议密度函数。由于大跨径斜拉桥施工风险状况复杂,难以指定合适的建议密度函数,故采用Gibbs抽样算法进行数值模拟。
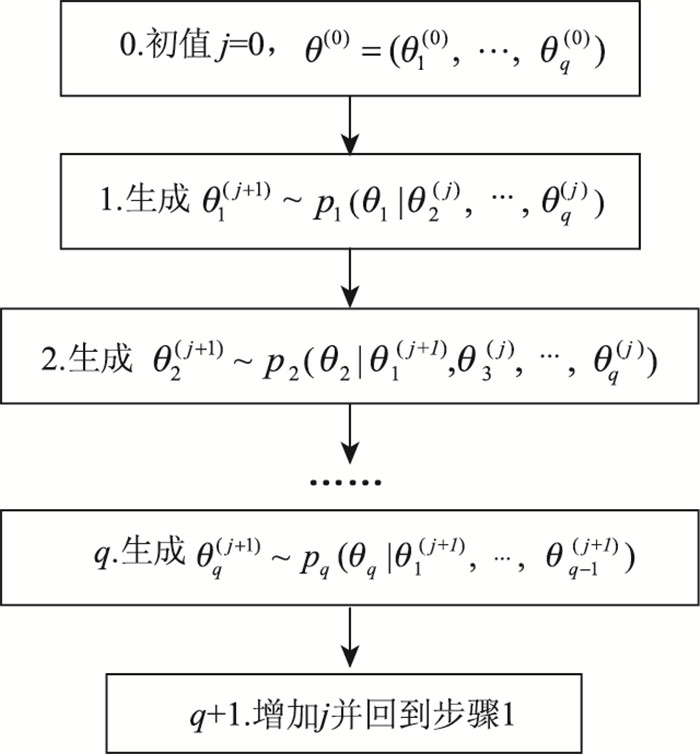
假设参数向量θ包含q个元素θ=(θ1,θ2, …,θq),每个元素的条件后验分布为:p1(θ1|θ2, …, θq, data),p2(θ2|θ1, θ3, …, θq, data), …, pq(θq|θ1, …, θq-1, data)。直接从参数向量θ中生成样本比较困难,但从各个条件后验密度p1,p2, …,pq中产生仿真数据是可能的。Gibbs抽样算法的基本流程如图 1所示。
|
| 图 1 Gibbs抽样算法基本流程 Fig. 1 Basic process of Gibbs sampling algorithm |
| |
图 1中,当初值j=0时,θ1(j+1)实质为θ1(1),θ2(j+1)实质为θ1(2),流程图中第1步至第q步计算的就是上文中提到的各元素的条件后验分布,第q+1步,j=2,重新计算各元素的条件后验分布,多次迭代后获得以获得足够多的样本,再进行统计分析。
1.3 收敛性分析MCMC算法经过多次迭代可以获得从后验分布中获得的样本,只有抽样算法保证收敛才能认为这种近似是足够精确的。MCMC算法的收敛性可以从两个方面进行判定。
由于MCMC初值一般距离后验分布较远,算法需要运行一定次数后,才能认为是后验分布的合理近似,收敛于后验分布之前的迭代称为老炼。观察θ中的元素对应迭代次数所获得的仿真值的轨迹图,老炼期的数据表现出显著变化,收敛后数据则较为稳定。
另外,仿真样本的自相关性也可以判断算法是否收敛。MCMC算法中衡量仿真样本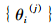
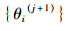
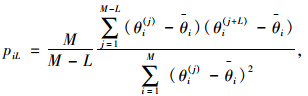
|
(1) |
式中,piL为自相关函数值; M为老炼后的样本数目;L为两个仿真数据集间隔的迭代次数;θi为后验均值的估计。当L=1时,抽样算法的自相关函数通常为正值,随着L的增加逐渐减少到0,此时可认为算法收敛。
2 补偿竞争风险聚合算法(CCRAA)大跨径斜拉桥施工过程属于一个庞大的系统,各类风险因素众多,要想判断某施工阶段或整个项目的风险就应进行风险聚合。风险聚合是指当存在多个风险时考虑各风险的综合影响,常见的方法有风险值求和(Sum),求最大风险值(Max)以及求风险质心(Centroid)等[11-13]。Sum法和Max法在风险聚合时易出现极值,Centroid法则易对风险概率产生依赖。当风险概率的和值为1时,Centroid法就演变为工程实际中常用的风险评估方法—模糊综合评判法。补偿竞争风险聚合算法则可以克服以上缺点,先对各风险值进行补偿,再向聚类中心聚集,能取得比传统聚合方法更客观的聚合风险[14]。
2.1 模糊聚类模糊聚类是将聚类中心作为该类样本的特征,聚类中心一般不是实际样本,而是该聚类的一个虚拟理想样本,它的指标综合反映了该类指标的特性[15]。在聚类群体中,一个合理的聚类中心应当与各样本的距离越小越好,本研究采用海明距离描述聚类群体样本与聚类中心之间的线性距离。
设A和B是论域U上的两个模糊子集,A和B之间的海明距离(也称为绝对海明距离)d(A,B)定义为:
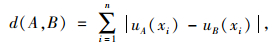
|
(2) |
式中,uA(xi), uB(xi)分别为论域中A集合与B集合中各点x方向的坐标值。
实际应用中的相对海明距离δ(A, B)可以表示为:
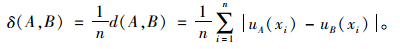
|
(3) |
将风险门限Riskthr设为风险集合的聚类中心,称为基值;s表示绝对海明距离,即各风险值到基值的距离之和;s′表示相对海明距离,即各风险值到风险基值的平均距离,具体计算式为:
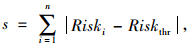
|
(4) |
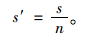
|
(5) |
以Riskthr为聚类中心,风险值为聚类样本。风险补偿的目的就是减少Riskthr与风险值之间的绝对海明距离s,使风险值群体向聚类中心靠近。风险补偿是将风险值与Riskthr之间的相对海明距离s′按比例对各风险值进行补偿,缩小风险值与聚类中心的距离,风险取值区间为[Riskstar, Riskend]。风险补偿规则定义为:
规则1 风险补偿需保持风险和值不变。
规则2 补偿后聚合风险Riskaggr∈[Riskstar, Riskend],Riskaggr应尽可能接近聚类中心,提高聚合结果的稳定性。
以m个风险值为例,首先将风险值由小到大构成风险值序列,当m为偶数时,序列号中值介于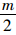
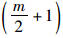
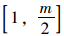
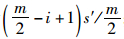
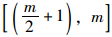
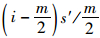
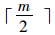
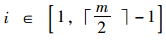
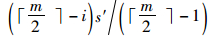
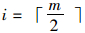
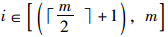
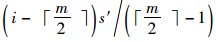
比较补偿后的风险值,计算Riskmin和Riskmax的平均值作为聚合风险Riskaggr,相比于Riskmin和Riskmax,Riskaggr更接近于Riskthr。风险聚合算法生成的Riskaggr具有风险综合效应,且与风险数量无关。
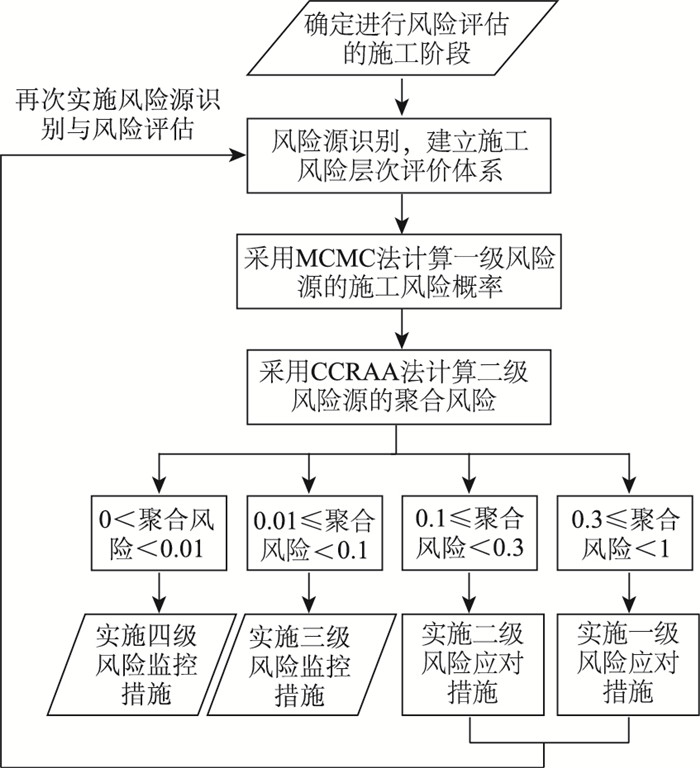
3 施工风险预警模型大跨径斜拉桥施工过程复杂,施工风险评估应针对某相对独立的施工阶段,当评估发现该施工阶段存在较大风险时,应立即采取风险应对措施,降低施工风险。在进行施工风险评估之前,应先进行风险源识别,建立施工风险层次评价体系,各施工阶段为二级风险源,具体施工风险为一级风险源。在大跨径斜拉桥施工风险预警模型中,采用MCMC法得到的是一级风险源的施工风险概率,CCRAA法则可将各风险聚合得到整个施工阶段的风险概率,以此作为风险决策的依据。
结合文献[16]中风险概率等级与施工过程的实际情况,大跨径斜拉桥施工风险等级根据风险概率划分为:低风险、中等风险、高风险、极高风险,对应的概率区间为(0, 0.01),[0.01, 0.1),[0.1, 0.3),[0.3, 1),此概率区间的意思是指,风险概率越高,事故发生的可能性越大,即认为事故发生可能性大的施工过程为高风险施工过程,通过本研究方法计算得到的施工风险概率可直接作为该施工安全事故发生的概率,因此当施工风险概率大于等于0.1时,可认定为高风险安全事故。通常认为事故后果严重的风险事件发生概率小,发生概率大的风险事件造成的事故后果轻微,所以常见的对于施工事故风险等级的划分从事故发生的可能性(又称事故发生概率)与事故的严重程度(又称事故造成的后果或风险损失)两方面进行综合考虑[16-17],但此时忽略了建筑施工过程中“安全第一”与“预防为主”的原则[18],因此任何一个轻微事故都不应当忽略,一个轻微事故均有可能引起一场严重事故,故本研究仅从事故发生可能性即施工风险概率方面对施工风险等级进行划分。
对于实施了风险应对措施的施工阶段应进行二次评估,保证施工风险降低到合理可控的范围内,具体的大跨径斜拉桥施工风险预警模型见图 2。
|
| 图 2 大跨径斜拉桥施工风险预警模型 Fig. 2 Construction risk early warning model for long-span cable-stayed bridge |
| |
4 工程实例分析
中朝鸭绿江界河公路大桥及接线是我国连接朝鲜的重要通道,大桥全长3.026 km,其中主桥采用(86+229+636+229+86) m的五跨双塔双索面钢箱梁斜拉桥方案,结构体系为五跨连续半漂浮体系,桥梁支座均采用耐腐蚀型球型钢支座。主梁采用流线型扁平钢箱梁,正交异性钢桥面板,顶、底板及下腹板采用U型肋加劲,中心线处梁高3.5 m,梁全宽33.5 m,主梁标准梁段长16 m,梁的外侧设置三角形风嘴。索塔采用H型,C50混凝土现浇,索塔总高度194.6 m,底部设置2.5 m高的塔座。斜拉索采用镀锌钢丝斜拉索,辅助墩及过渡墩均采用箱型墩。
该大桥主跨为636 m,属于大跨径斜拉桥,施工过程中发生安全事故的可能性较大,应采用大跨径斜拉桥施工风险预警模型对其进行风险预警与风险控制。
4.1 风险源识别该大桥主桥按照施工工序可划分为桩基础施工、钢吊(套)箱施工、承台施工等10个施工阶段,结合文献[2]中的风险源识别方法,参照《企业职工伤亡事故分类标准》(GB 6441—86) 中人员安全事故分类标准,考虑施工过程中的结构安全,构建大跨径斜拉桥施工风险层次评价体系,见表 1。该层次评价体系的构建基础是不同的施工阶段,表中的施工阶段及对应的风险源均为常见,故该层次评价体系具有通用性,但对于不同的斜拉桥应结合实际情况进行构建。
| 序号 | 二级风险源 | 一级风险源 |
| 1 | 桩基础施工(u1) | 桩孔歪斜(u11)、坍孔(u12)、钢筋笼变形过大(u13)、坍塌事故(u14)、机械伤害(u15)、起重事故(u16) |
| 2 | 钢吊(套)箱施工(u2) | 钢吊箱失稳(u21)、龙门吊倒塌(u22)、千斤顶失效风险(u23)、油压系统失效风险(u24)、高处坠落(u25)、物体打击(u26)、船撞(u27) |
| 3 | 承台施工(u3) | 大体积混凝土浇注产生裂缝(u31)、钢筋安装精度不够(u32)、机械伤害(u33)、起重事故(u34)、船撞(u35) |
| 4 | 下塔柱及下横梁支架现浇施工(u4) | 模板及支架失效(u41)、预应力管道安装偏差(u42)、锚下局部混凝土开裂(u43)、高处坠落(u44)、机械伤害(u45)、物体打击(u46) |
| 5 | 塔柱爬模施工(u5) | 索塔倾斜(u51)、爬模系统构件坠落(u52)、爬模模板架坍塌(u53)、起重事故(u54)、物体打击(u55)、高处坠落(u56) |
| 6 | 钢箱梁制作(u6) | 钢箱梁焊接质量不达标(u61)、胎架制作精度不足(u62)、U形肋腐蚀(u63)、物体打击(u64)、机械伤害(u65)、火灾与爆炸(u66) |
| 7 | 斜拉索安装(u7) | 索套管偏差(u71)、斜拉索张拉不同步(u72)、撑脚失效(u73)、斜拉索张拉程序及张拉力调整不当(u74)、施工荷载及不平衡施工影响(u75)、起重事故(u76)、机械伤害(u77) |
| 8 | 钢箱梁悬拼施工(u8) | 钢箱梁悬拼过程失稳(u81)、钢箱梁环缝焊接收缩(u82)、钢箱梁轴线偏位(u83)、临时固结失效(u84)、机械伤害(u85)、起重事故(u86)、火灾与爆炸(u87) |
| 9 | 主梁合龙(u9) | 荷载施加不当(u91)、温度对合龙的影响(u92)、体系转换未按要求(u93)、机械伤害(u94)、起重事故(u95)、高处坠落(u96) |
| 10 | 桥面系及附属工程(u10) | 结构损伤(u101)、机械伤害(u102)、物体打击(u103)、溺水(u104) |
表 1中的起重事故、坍塌事故、机械伤害、淹溺事故、高处坠落、火灾与爆炸、物体打击等均为人员安全事故,其余为结构安全事故。
由于斜拉桥施工阶段较多,限于篇幅,仅对钢箱梁悬拼施工进行施工风险评估分析,其他施工阶段风险评估过程类似。
4.2 计算施工风险概率依据文献[17]中的典型风险评估矩阵,风险等级一般划分为5级,对应的风险值为{1, 2, 3, 4, 5}。根据贝叶斯理论,假定桥梁施工风险值服从正态分布。邀请15位专家,每3人分为1组,估计钢箱梁悬拼施工阶段7个一级风险源的风险值,以此作为评估样本,具体评估结果见表 2。
| 专家 | u81 | u82 | u83 | u84 | u85 | u86 | u87 |
| 专家1 | 1 | 3 | 4 | 4 | 3 | 2 | 1 |
| 专家2 | 2 | 3 | 4 | 4 | 4 | 3 | 1 |
| 专家3 | 1 | 4 | 4 | 3 | 3 | 2 | 2 |
| 专家4 | 1 | 4 | 4 | 4 | 4 | 3 | 2 |
| 专家5 | 2 | 3 | 4 | 4 | 3 | 2 | 2 |
表 2中第i行第j列的风险值来自于风险值总体Yij,且Yij服从正态分布:
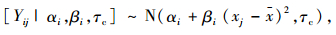
|
(6) |
式中,αi, βi, τc均为未知参数,可假定其先验分布分别为:[αi|αc, τc]~N(αc, τa), βi|βc, τc]~N(βc, τβ), [τc]~Gamma(0.001, 0.001)。τc的先验分布均值为1,方差很大,达到了1 000,此时表明该分布对τc一无所知,为无信息先验分布。αc,τα,βc,τβ为超参数,同样采用无信息先验分布分别为:[αc]~N(0, 10-6),τα~Gamma(0.001, 0.001),[βc]~N(0, 10-6),[τβ]~Gamma(0.001, 0.001)。
为运用Gibbs抽样算法,应先确定各参数的条件分布。根据贝叶斯理论,通过公式推导可得各参数的条件分布分别为:
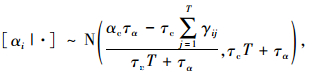
|
(7) |
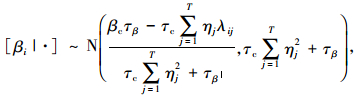
|
(8) |
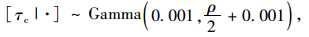
|
(9) |
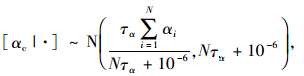
|
(10) |
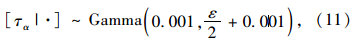
|
(11) |
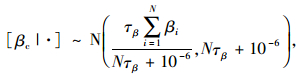
|
(12) |
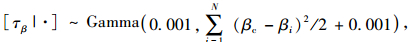
|
(13) |
式中,γij=βi(xj-x-)2-Yij,N=5,T=7,ηj=(xj-x-)2,λij=αi-Yij,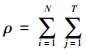
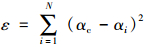
采用图 1所示的Gibbs抽样算法基本流程,结合上述条件分布与先验分布抽取52 000个样本,由于迭代开始后数据并不稳定,不具有参考价值,故舍弃前2 000个样本,对后50 000个样本进行统计分析,取初值α=(3, 3, 3, 3, 3),β=(1, 1, 1, 1, 1),αc=2,βc=1,τα=1,τβ=1,τc=1。部分主要变量采样结果见图 3~图 4及表 3。
|
| 图 3 参数的迭代样本轨迹 Fig. 3 Iterative sample trajectory of parameters |
| |
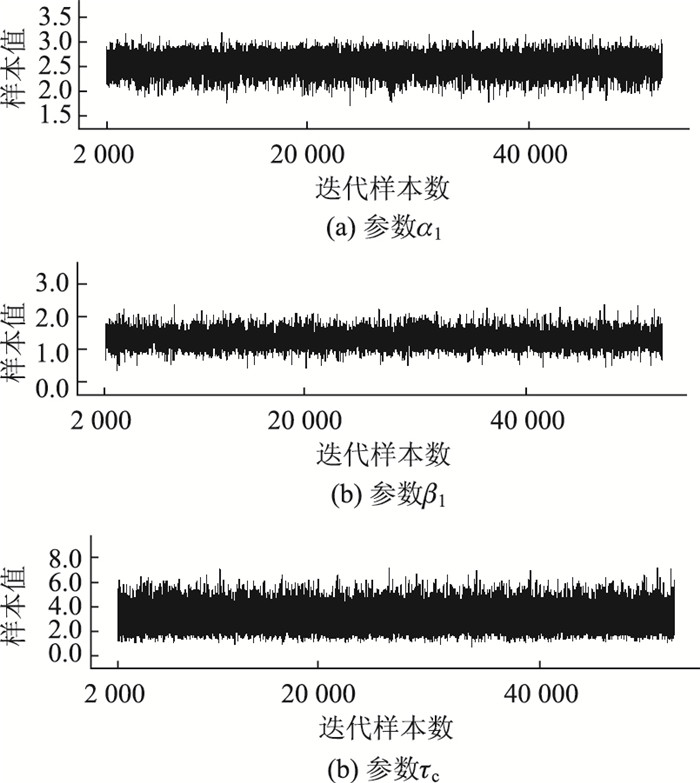
|
| 图 4 参数的自相关函数 Fig. 4 Auto correlation functions of parameters |
| |
| 变量 | 均值 | 标准差 | 2.5%分位值 | 中位数 | 97.5%分位值 | 采样起点 | 样本数 |
| α1 | 2.593 | 0.159 8 | 2.237 | 2.606 | 2.875 | 2 001 | 50 000 |
| α2 | 2.714 | 0.148 4 | 2.436 | 2.708 | 3.032 | 2 001 | 50 000 |
| α3 | 2.636 | 0.148 2 | 2.321 | 2.643 | 2.914 | 2 001 | 50 000 |
| α4 | 2.753 | 0.160 5 | 2.471 | 2.74 | 3.111 | 2 001 | 50 000 |
| α5 | 2.677 | 0.144 9 | 2.387 | 2.676 | 2.965 | 2 001 | 50 000 |
| β1 | 1.316 | 0.185 4 | 0.969 9 | 1.31 | 1.709 | 2 001 | 50 000 |
| β2 | 1.288 | 0.180 0 | 0.938 7 | 1.286 | 1.655 | 2 001 | 50 000 |
| β3 | 1.242 | 0.184 8 | 0.855 1 | 1.248 | 1.599 | 2 001 | 50 000 |
| β4 | 1.312 | 0.184 7 | 0.966 6 | 1.306 | 1.704 | 2 001 | 50 000 |
| β5 | 1.235 | 0.187 1 | 0.839 5 | 1.244 | 1.588 | 2 001 | 50 000 |
| τc | 3.099 | 0.784 | 1.759 | 3.031 | 4.818 | 2 001 | 50 000 |
图 3表明老炼期过后各参数迭代结果稳定,图 4表明随着迭代次数的增加,参数的自相关函数值逐渐降为0。综合以上两点可判定MCMC算法收敛,计算结果足够精确可靠。
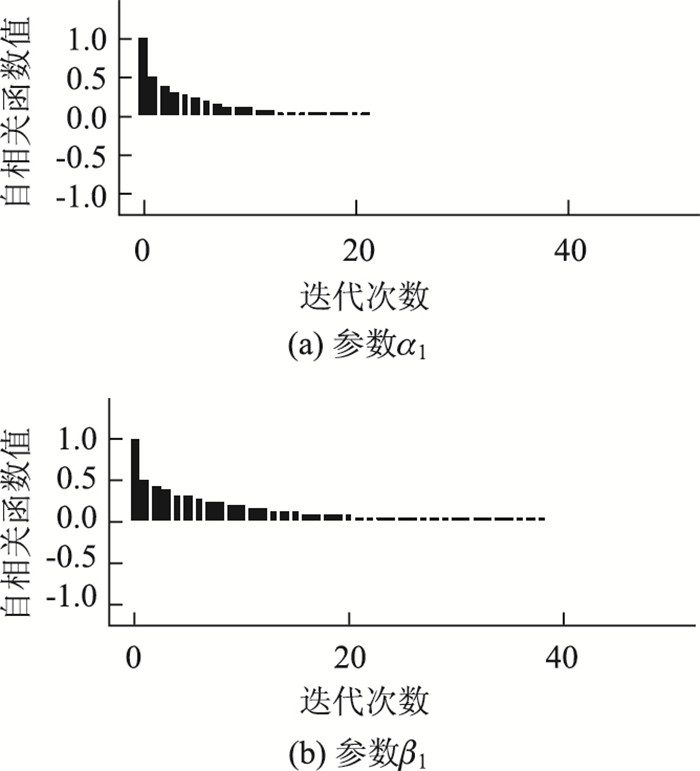
将各参数的估计值代入式(6),可以得到各一级风险源的风险值分布。风险值≥4,表明该施工过程风险较大,结合风险值分布计算风险值≥4的发生概率。图 5为专家组2对风险源u85评估后,采用MCMC法进行仿真模拟得到的概率分布,图中小于4的面积值为0.905 6,大于等于4的面积值0.094 4即为风险概率。计算各施工风险源的风险概率均值,作为一级风险源施工风险概率,结果见表 4。
|
| 图 5 专家组2对风险源u85的模拟风险概率分布 Fig. 5 Simulation risk probability distribution of expert group 2 to risk source u85 |
| |
| 一级风险源 | u81 | u82 | u83 | u84 | u85 | u86 | u87 |
| 风险概率 | 0.008 | 0.012 | 0.416 | 0.210 | 0.076 | 0.011 | 0.010 |
4.3 风险聚合
根据大桥施工的实际情况,结合专家意见,确定钢箱梁悬拼施工阶段的风险概率基值为0.1。通过式(2)~式(5) 计算各一级风险源风险概率到基值之间的相对海明距离为0.115 6,采用2.2节中的风险补偿算法,得到一级风险源风险概率的补偿值,具体结果见表 5。
| 风险源 | u81 | u82 | u83 | u84 | u85 | u86 | u87 |
| 补偿值 | 0.115 6 | 0 | 0.115 6 | 0.077 | 0.038 5 | 0.038 5 | 0.077 |
| 补偿后的风险概率 | 0.123 6 | 0.012 | 0.300 4 | 0.133 0 | 0.037 5 | 0.049 5 | 0.087 |
比较补偿后的风险概率,得到风险区间[0.012, 0.300 4],则二级风险源的聚合风险Riskaggr为0.156 2,即钢箱梁悬拼施工阶段的发生安全事故的概率为0.156 2。
4.4 施工风险预警根据图 2中所示的大跨径斜拉桥施工风险预警模型,钢箱梁悬拼施工阶段的聚合风险介于0.1到0.3之间,属于高度风险,应立即实施二级风险应对措施,加强施工过程的安全保障。各项安全整改措施到位后,再次实施风险源识别与风险评估,确保该施工阶段的聚合风险降到0.1以下,同时采取相应的风险监控措施,最大限度地降低事故发生概率。
5 结论本研究构建了大跨径斜拉桥施工风险预警模型,研究了MCMC算法与CCRAA算法在预警模型中的有效运用,并通过工程实例进行了计算分析,得出以下结论:
(1) 采用MCMC算法可以最大限度地利用已有信息,解决大跨径斜拉桥施工风险信息匮乏的难点,通过数值模拟方法直接从后验分布中生成参数向量的仿真样本,并进行多维随机变量的统计推断。工程实例证明了施工风险概率计算结果解释性强,实现了客观理论推断与主观认知的统一,兼具客观概率估计和主观概率估计方法的优势,同时避免了两类方法的缺点,计算结果可靠。
(2) CCRAA算法考虑了多个风险的综合效应,依据模糊聚类的基本规则,使施工风险概率计算结果向风险概率基值聚集,聚合过程稳定,相比于传统风险聚合方法更加客观,计算效率高。
(3) 基于以上两种方法,构建了大跨径斜拉桥施工风险预警模型,以实施施工风险的二次评估,确保将施工风险降低到合理可控的区间,表明了施工风险预警的有效性。
(4) 在采用MCMC法进行抽样之前,首先必须保证已有信息的准确性,否则后续计算结果的可靠性无从谈起。CCRAA算法对风险基值具有依赖性,如果风险基值发生变化,那么风险聚合结果也可能发生幅度有限的变化,因此风险基值的确定至关重要。
| [1] | 巩春领. 大跨度斜拉桥施工风险分析与对策研究[D]. 上海: 同济大学, 2006. GONG Chun-ling. Construction Risk Analysis and Countermeasures Research of Long Span Cable-stayed Bridge[D].Shanghai:Tongji University, 2006. |
| [2] | 安朗, 张昕然. 整体吊装钢管混凝土系杆拱桥非线性模糊评判[J]. 公路交通科技, 2015, 32(10): 91-96 AN Lang, ZHANG Xin-ran. Nonlinear Fuzzy Evaluation of Construction Risk of Integral Hoisting CFST Tied Arch Bridge[J]. Journal Highway and Transportation Research and Development, 2015, 32(10): 91-96 |
| [3] | 郑祖恩, 李智勇, 吴欣. 基于模糊综合评判法的预应力混凝土连续梁桥悬臂浇筑施工风险评估[J]. 公路工程, 2013, 38(2): 60-64 ZHENG Zu-en, LI Zhi-yong, WU Xin. Cantilever Irrigating Construction Risk Assessment of Prestressed Concrete Continuous Beam Bridge Based on Fuzzy Comprehensive Evaluation Method[J]. Highway Engineering, 2013, 38(2): 60-64 |
| [4] | 陈国华, 吴武生, 徐三元, 等. 基于WBS-RBS与AHP的跨海桥梁工程施工HSE风险评价[J]. 中国安全科学学报, 2013, 23(9): 51-57 CHEN Guo-hua, WU Wu-sheng, XU San-yuan, et al. Assessment HSE Risk of during Sea-crossing Bridges Project Construction Based on WBS-RBS and AHP[J]. China Safety Science Journal, 2013, 23(9): 51-57 |
| [5] | 刘育新. PC斜拉桥施工期风险分析研究[D]. 西安: 长安大学, 2013. LIU Yu-xin. Research on Risk Analysis of PC Cable-stayed Bridges during Construction[D]. Xi'an:Chang'an University, 2013. |
| [6] | 王小飞. 大跨径斜拉桥施工安全风险预警系统研究[D]. 重庆: 重庆交通大学, 2014. WANG Xiao-fei. Study on Construction Safety Risk Early-warning System of Long-span Cable-stayed Bridge[D].Chongqing:Chongqing Jiaotong University, 2014. |
| [7] | 赵延龙. 基于贝叶斯网络的大跨径斜拉桥上部结构施工安全风险分析与控制[D]. 重庆: 重庆交通大学, 2013. ZHAO Yan-long. Construction Security Risks Analysis and Control of Superstructure of Long-span Cable-stayed Bridge Based on Bayesian Belief Network[D].Chongqing:Chongqing Jiaotong University, 2013. |
| [8] | PANAGIOTIS M, MANOJ N. New Method for Measuring the Safety Risk of Construction Activities:Task Demand Assessment[J]. Journal of Construction Engineering and Managment, 2011, 137(1): 30-38 |
| [9] | ZHU Ben-jin, FRANGOPOL D M. Risk-based Approach for Optimum Maintenance of Bridges under Traffic and Earthquake Loads[J]. Journal of Structure Engineering, 2013, 139(3): 422-434 |
| [10] | MICHAEL H, ALYSON W, SHANE R, et al. Bayesian Reliability[M]. New York: Springer, 2008. |
| [11] | CHAPIN P, SKALKA C, WANG X S. Risk Assessment in Distributed Authorization[C]//Proceedings of the 2005 ACM Workshop on Formal Methods in Security Engineering. New York:ACM, 2008:33-41. |
| [12] | BARACALDO N, JOSHI J. A Trust-and-risk Aware RBAC Framework:Tackling Insider Threat[C]//Proceedings of the 17th ACM Symposium on Access Control Models and Technologies. New York:ACM, 2012:167-176. |
| [13] | CHARI S, LOBO J, MOLLOY I. Practical Risk Aggregation in RBAC Models[C]//Proceedings of the 17th ACM Symposium on Access Control Models and Technologies. New York:ACM, 2012:117-118. |
| [14] | 王建军, 李建平, 杜仕甫. 基于模糊聚类的无权值风险综合评判算法[J]. 系统工程理论与实践, 2015, 35(8): 2137-2143 WANG Jian-jun, LI Jian-ping, DU Shi-fu. Fuzzy-clustering-based Unweighted Risk Overall Evaluation Algorithm[J]. Systems Engineering-Theory & Practice, 2015, 35(8): 2137-2143 |
| [15] | 李士勇. 工程模糊数学及应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2004. LI Shi-yong. Engineering Fuzzy Mathematics with Applications[M]. Harbin: Harbin Institute of Technology Press, 2004. |
| [16] | 交通运输部工程质量监督局. 公路桥梁和隧道工程施工安全风险评估制度及指南解析[M]. 北京: 人民交通出版社, 2012. Engineering Quality Supervision Bureau of Ministry of Transport. Safety Risk Assessment System and Guide for Construction of Highway Bridge and Tunnel[M].Beijing:China Communications Press, 2012. |
| [17] | 阮欣, 尹志逸, 陈艾荣. 风险矩阵评估方法研究与工程应用综述[J]. 同济大学学报:自然科学版, 2013, 41(3): 381-385 RUAN Xin, YIN Zhi-yi, CHEN Ai-rong. A Review on Risk Matrix Method and Its Engineering Application[J]. Journal of Tongji University:Nature Science Edition, 2013, 41(3): 381-385 |
| [18] | JTJ 076-95, 公路工程施工安全技术规程[S]. JTJ 076-95, Safety Technology Rules for Highway Engineering Construction[S]. |
 2017, Vol. 34
2017, Vol. 34
