扩展功能
文章信息
- 刘靖宇, 刘朝晖, 王旭东, 黄优
- LIU Jing-yu, LIU Zhao-hui, WANG Xu-dong, HUANG You
- 动态回弹模量滞回曲线形态参数研究
- Study on Morphological Parameters of Hysteretic Curve of Dynamic Resilient Modulus
- 公路交通科技, 2017, 34(10): 6-12
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(10): 6-12
- 10.3969/j.issn.1002-0268.2017.10.002
-
文章历史
- 收稿日期: 2017-03-17
2. 交通运输部公路科学研究院, 北京 100000
2. Research Institute of Highway, Ministry of Transport, Beijing 100000, China
滞回曲线(hysteretic curve),指在循环加载下试件的荷载-变形曲线,反映试件在循环荷载作用下的刚度退化、能量消耗及其他变形特征,也称恢复力曲线(restoring force curve)。基于滞回曲线已有不少研究,包括:(1) 对梁、柱节点,框架及剪力墙等结构的延性和吸能抗震能力的滞回曲线研究[1-2];(2) 青藏冻结黏土、兰州黄土、岩石等黏弹材料本构关系的滞回曲线研究[3-4];(3) 基于能量耗散原理的滞回曲线疲劳特性研究,研究对象主要是金属合金类材料[5-6],也有学者利用沥青混合料复数模量滞回曲线面积进行疲劳特性研究[7-9]。
近年来,国内外沥青混合料动态抗压回弹模量的研究日趋成熟[10-15],遗憾的是,动态模量研究大多聚焦在模量本身,忽略了混合料循环加、卸载过程滞回曲线反馈的数据信息。为此,对动态抗压回弹模量的滞回曲线进行分析计算,建立了3项滞回曲线的形态参数(包括长轴斜率k、离心率e、椭圆面积S),并利用MTS-810对4种沥青混合料进行不同温度下的逐级半正弦波加载动态抗压回弹模量试验,结合其试验结果对所得动态抗压回弹模量的滞回曲线形态参数进行研究。
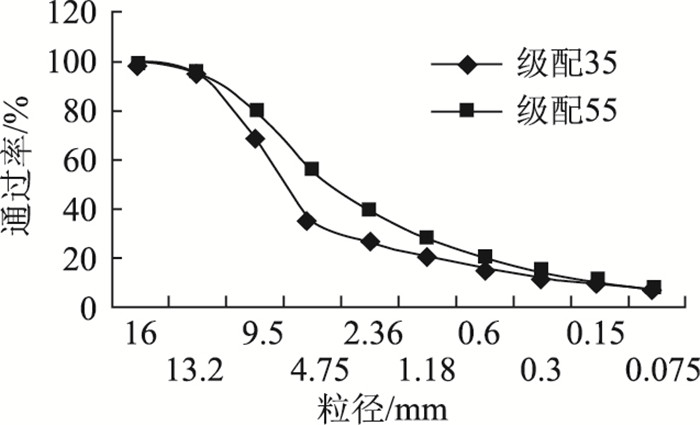
1 试验方法及原理 1.1 试验方法采用秦皇岛70#基质沥青及SBS改性沥青,级配为AC13-35和AC13-55(35和55分别代表级配关键筛孔4.75的通过率为35%和55%),如图 1所示,从SGC试件中钻芯取样得到Φ100 mm×100 mm的试件[15],并打磨以确保端面平整和光滑[16-17]。采用MTS-810对试件进行单轴无侧限的动载试验并按顶面法及侧面法进行数据采集,如图 2所示:在试件顶面水平放置一个直径大于MTS压头的圆形承载板以减小端部滑移,沿承载板的直径两端各放置一个线性位移传感器LVDT(Linear variable differential transducers);将水平和竖向应变片组成的T形应变花粘贴在试件侧面中部,沿圆周等间距安放3组(即夹角120°)。通过中心MTS竖向位移传感器和顶面两端线性位移传感器来采集试件顶面变形情况,通过紧密粘贴在试件侧面的应变花来采集试件侧面的变形情况。
|
| 图 1 级配35和55通过率 Fig. 1 Pass rates of gradation 35 and gradation 55 |
| |

|
| 图 2 MTS-810抗压回弹模量试验 Fig. 2 MTS-810 compression resilient modulus test |
| |
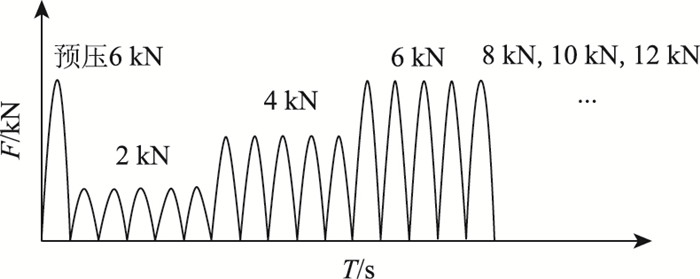
动态抗压回弹模量的加载波形如图 3所示,每级荷载加载200个周期,并采集最后10个稳定周期的平均荷载和变形进行研究[18]。
|
| 图 3 动态模量试验加载波形 Fig. 3 Loading waveform of dynamic modulus test |
| |
1.2 形态参数的建立
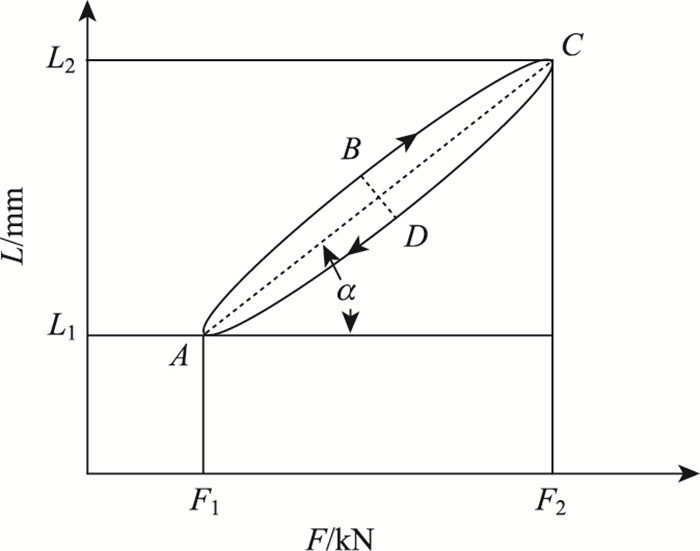
小变形下的沥青混合料处于黏弹性变形区间,其滞回曲线近似为闭合的椭圆,如图 4所示,椭圆ABCD为单个加载周期下的荷载-变形滞回曲线,F和L分别为任一加载时刻的荷载和轴向变形。点A,C分别为加载的起点和终点,弧线ABC为加载变形曲线,弧线CDA为卸载变形恢复曲线。
|
| 图 4 滞回曲线示意图 Fig. 4 Schematic diagram of hysteresis curve |
| |
1.2.1 长轴斜率k
由图 4,长轴斜率
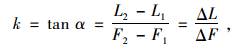
|
(1) |
式中k的单位为mm/kN。
抗压回弹模量
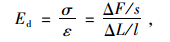
|
(2) |
式中,ΔF和ΔL分别为轴向荷载及可恢复变形;s和l分别为试件横截面积和高度。将上述两式合并,可得:
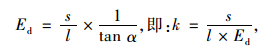
|
(3) |
式中,长轴倾角α∈(0°~90°)。对于任一试件其s和l都是定值,故可知斜率k与Ed成反比关系,换言之,滞回曲线长轴斜率k是表征沥青混合料动态抗压回弹模量的指标:k越大,沥青混合料的Ed越小;k越小,沥青混合料的Ed越大。
1.2.2 离心率e离心率是椭圆扁平程度的量度,单位为1,定义为椭圆焦距与长轴长的比值,常用e表示,即
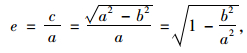
|
(4) |
式中,c为半焦距; a为长半轴; b为短半轴。离心率e可以理解为在长轴不变的情况下两个焦点离开椭圆圆心的距离,即滞回曲线的宽窄程度。e越大,滞回曲线越狭窄,黏滞性越小;e越小,滞回曲线越宽厚,黏滞性也越大。
1.2.3 滞回曲线面积S在图 4中,曲线ABC与线段F1F2所围面积表示加载过程中混合料获得的能量,曲线ADC与线段F1F2所成面积表示卸载过程中混合料释放的能量,二者的面积差,即滞回曲线的面积S,代表一个加载周期中混合料的耗散能Wi,即:
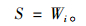
|
(5) |
采用有向梯形法计算S,滞回曲线上相邻两点与F轴所围的有向梯形的面积为:
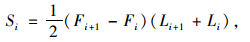
|
(6) |
式中,(Fi,Li)为滞回曲线上第i点的坐标。Si在加载过程是正值,卸载过程是负值, 单位为kN·mm,即焦耳J。滞回曲线上各有向梯形的代数和就是滞回曲线的面积,即:
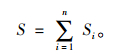
|
(7) |
滞回曲线面积S,等于混合料单个加载周期内的耗散能,反映其能量耗散能力。S越大,加、卸载过程中能量损耗越大,疲劳寿命越短;反之,S越小能量耗散就越小,其疲劳寿命越长。
2 滞回曲线形态参数试验研究上述分别分析了滞回曲线的形态特征参数k,e,S的计算依据和力学意义,并进行平行试验以研究不同试验温度、不同混合料类型、不同荷载级位下各个形态特征参数变化规律,以下基于试验结果分别讨论。
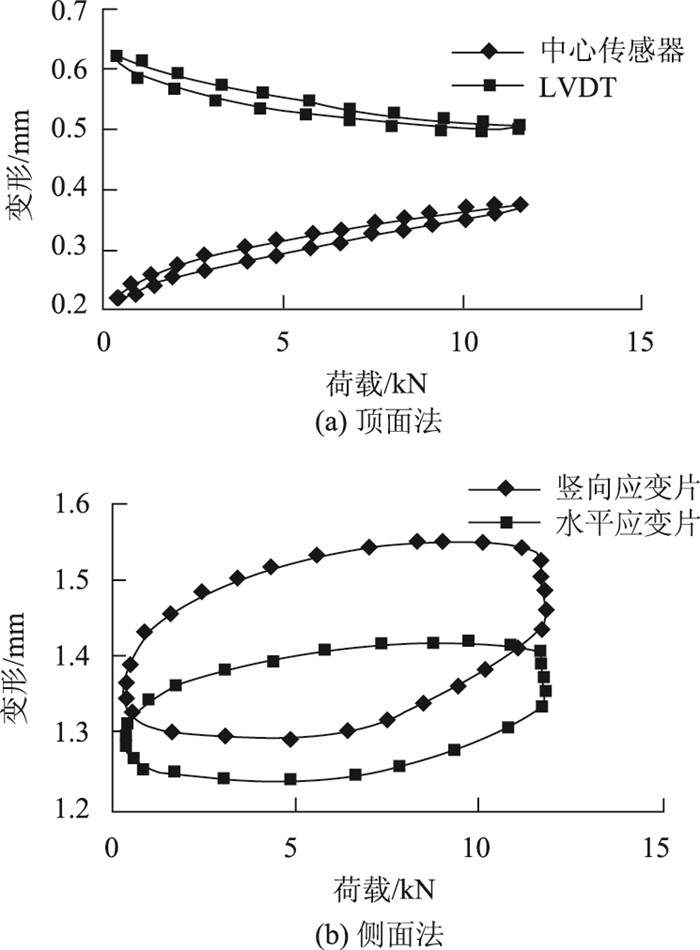
2.1 不同数据采集方法的形态参数图 5为径高比1:1试件不同变形采集方法得到的滞回曲线形态图,采集方式包括:(1) 试件顶面中心传感器; (2) 试件顶面两端架设的LVDT; (3) 试件侧面中部垂直方向应变片; (4) 水平方向粘贴的应变片。
|
| 图 5 不同方法采集的滞回曲线 Fig. 5 Hysteresis curves obtained by different methods |
| |
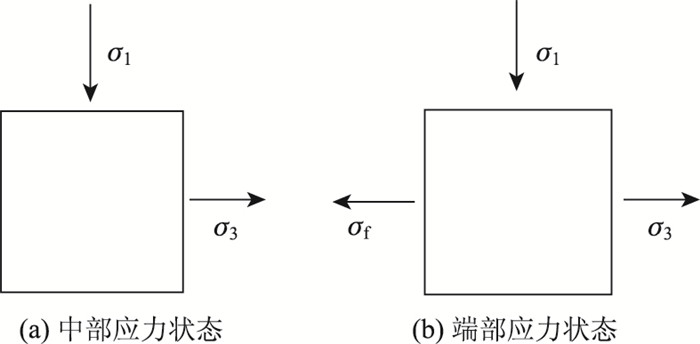
从不同试验方法的滞回曲线图可以看出,采用顶面法得到的滞回曲线都不是规则的椭圆形;而采用侧面法得到的竖向和水平滞回曲线更接近于椭圆形。为进一步分析其原因,在试件端部和中部任取一单元体进行受力分析,其力学状态见图 6。
|
| 图 6 中部和端部混合料应力状态 Fig. 6 Stress state of mixture at center and end |
| |
显然,除了受到的轴向压力σ1、侧向内力σ3外,端部混合料还将受到压头和底座带来的摩擦力σf,该摩擦力也可以理解为围压约束,最终导致试件的竖向变形减小,滞回曲线形态不规则。因此,后述进行的形态参数研究均采用侧面法所采集的滞回曲线。
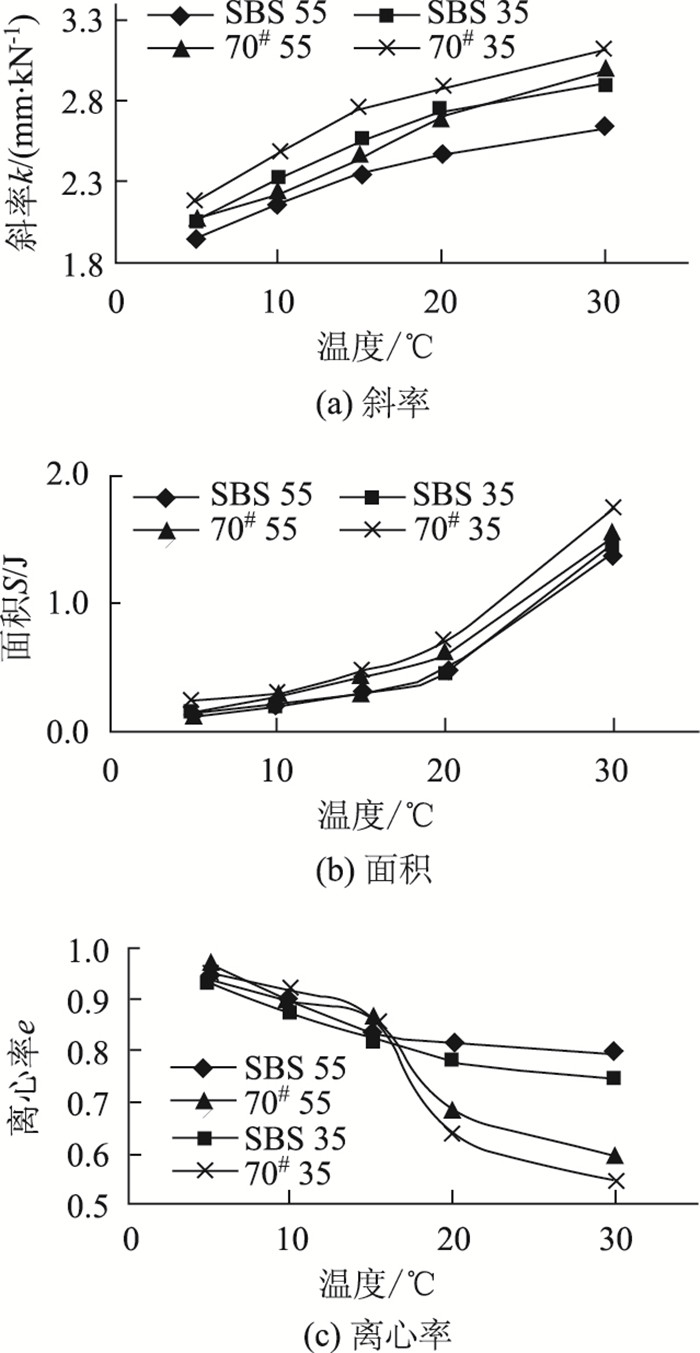
2.2 不同试验温度的形态参数4种沥青混合料的滞回曲线形态参数k,e,S随温度变化曲线见图 7,分析可知:
|
| 图 7 形态参数随温度变化曲线 Fig. 7 Curves of morphological parameters varying with temperature |
| |
(1) 从材料组成来看,4种材料的k,e,S取值均存在一定的差异,且SBS混合料总能比70#沥青混合料表现出更好的力学性能,说明混合料的沥青品质和级配组成均会影响其模量、黏滞性、耐疲劳性能,沥青品质对其性能的影响更为显著。
(2) k,e,S随温度变化呈现不同的变化趋势,其中k,S随温度升高而升高,e随温度升高而降低,说明随着温度升高,混合料模量及疲劳寿命衰减,黏滞性变大。
(3) 不论形态参数k,e,S随温度的升高存在何种变化趋势,其温度变化曲线均在15~20 ℃存在明显拐点。从黏弹材料的力学状态来说,这是因为该温度范围下的沥青混合料处于高弹态与黏流态转变区,兼有黏性流体和弹性固体的变形特性,且存在黏弹转化温度T∈(15~20 ℃),当温度t<T时,弹性占据主导地位;当温度t>T时,黏性占据主导地位,从而使得沥青混合料形态参数k,e,S在15~20 ℃表现出不同的发展趋势, 沥青混合料在15~20 ℃间存在黏弹特性改变,其力学性能发生明显转变。
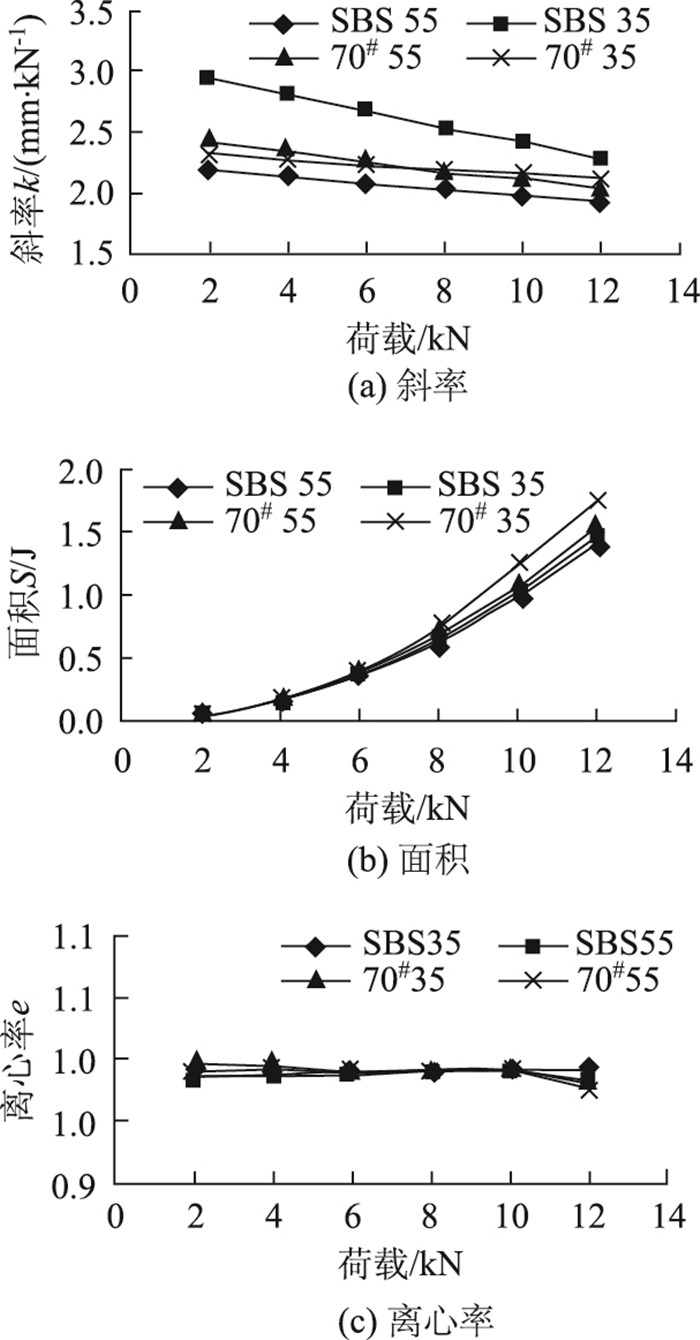
2.3 不同荷载的形态参数不同荷载级位下4种沥青混合料的形态参数k,e,S变化曲线见图 8,分析可知:
|
| 图 8 形态参数随荷载变化曲线 Fig. 8 Morphological parameters varying with load |
| |
(1)4种沥青混合料尽管性能有所差异,但都表现出随着荷载增加,斜率k减小、动态抗压回弹模量增加的趋势,即应力依赖性。
(2) 沥青品质与级配均会影响耗散能S的取值且沥青品质所起作用更大,另一方面4种混合料的耗散能随荷载增加呈幂函数变化趋势。
(3) 随着混合料类型和荷载级位变化,滞回曲线离心率e基本不变,说明混合料黏滞性与荷载强度无关。
3 形态参数的回归拟合总之,滞回曲线形态参数打破了以往的数据处理方法,能从动态试验过程反馈出沥青混合料的模量、黏滞性及耐疲劳性等力学信息。以下通过拟合和回归的方法进行力学建模。
3.1 基于斜率k的应力依赖模型图 8(a)反映了混合料在压缩状态下的应力依赖性。为了更准确地表征路面材料在实际服役过程中的力学状态,需要改变以往定值型的模量取值方法,建立回弹模量的应力依赖模型。以现行规范弯沉计算要求的20 ℃回弹模量为例,由式(3) 将k值换算成模量,并求得其平均值和代表值见表 1。
| 不同应力水平σ下的回弹模量 | ||||||||
| 材料 | σ | 0.24 | 0.50 | 0.75 | 1.01 | 1.26 | 1.52 | RT |
| 70#35 | 平均 | 1 555 | 1 606 | 1 667 | 1 717 | 1 784 | 1 854 | 7.69 |
| 代表 | 1 126 | 1 216 | 1 326 | 1 404 | 1 513 | 1 609 | ||
| 70#55 | 平均 | 1 518 | 1 580 | 1 650 | 1 715 | 1 794 | 1 877 | 9.31 |
| 代表 | 1 345 | 1 415 | 1 495 | 1 580 | 1 667 | 1 768 | ||
| SBS35 | 平均 | 1 511 | 1 560 | 1 616 | 1 678 | 1 726 | 1 792 | 9.2 |
| 代表 | 1 217 | 1 301 | 1 398 | 1 504 | 1 583 | 1 676 | ||
| SBS55 | 平均 | 1 701 | 1 748 | 1 800 | 1 861 | 1 910 | 1 969 | 11.0 |
| 代表 | 1 281 | 1 374 | 1 478 | 1 600 | 1 691 | 1 793 | ||
根据试验结果得到的4种混合料动态回弹模量及其相应温度下的无侧限抗压强度,可以建立相应的动态抗压回弹模量的应力依赖模型:
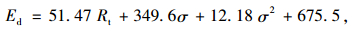
|
(8) |
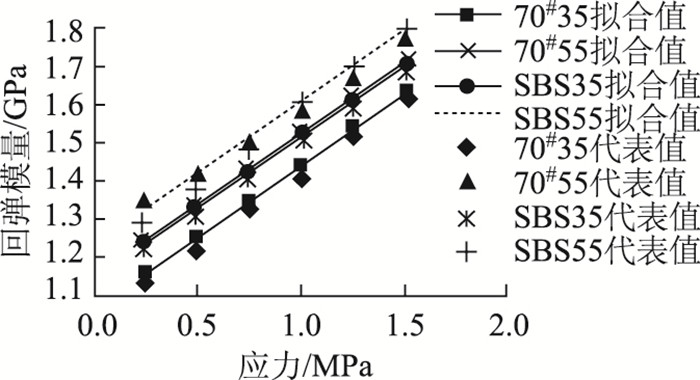
式中,Rt为相应温度下混合料的无侧限抗压强度;σ为应力,相关系数R2=0.931 3。不妨建立4种混合料对应荷载下的模型拟合值和实测代表值的比较图,如图 9所示。
|
| 图 9 逐级荷载下的代表值和拟合值 Fig. 9 Representative values and fitted values under progressive loading |
| |
从图 9来看,不论数值还是增长趋势4种沥青混合料在逐级荷载下的拟合值与代表值都极为接近,误差均在5%以内,表明所建立的应力依赖模型能较好地模拟材料在不同荷载下的回弹模量,其意义在于:
(1) 考虑了材料的应力依赖性,改变了定值模量的取值方式;
(2) 结合动态抗压回弹模量形态参数的研究及无侧限强度试验结果,可以对材料回弹模量的合理取值进行预估。
3.2 基于面积S的累积耗散能及疲劳方程 3.2.1 稳态耗散能的判定由于循环应力硬化效应,混合料抗变形能力随循环次数的增加而变大,在一定次数的循环加载后滞回曲线面积S值会趋于稳定。在对应荷载200次循环加载后,第201~210次加载的耗散能试验结果离散程度见表 2。
| 荷载/kN | 2 | 4 | 6 | 8 | 10 | 12 |
| 耗散能均值 | 37.2 | 173.0 | 388.1 | 698.7 | 1 069.8 | 1 531.7 |
| 均方差 | 2.06 | 0.95 | 1.58 | 3.07 | 7.06 | 3.47 |
| 变异系数/% | 5.6 | 0.5 | 0.4 | 0.4 | 0.7 | 0.2 |
从表 2可见,除了2 kN荷载下的耗散能本身取值较小导致的偏差外,大部分荷载级位下耗散能取值的离散性非常小,可以认为200次循环加载后混合料单个加载周期的耗散能已趋于稳定,即为稳态耗散能。
3.2.2 累积耗散能预测方程从图 7(b)可以看到4种混合料滞回曲线面积S值随荷载变化呈幂函数曲线,由此建立4种材料面积S与荷载的幂函数方程:
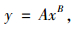
|
(9) |
式中A, B为材料参数。根据Miner疲劳损伤理论,对于加载n次、荷载级位为定值F的动态试验,可以通过式(10) 计算其累积耗散能:
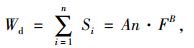
|
(10) |
式中,Si为第i次循环加载对应的滞回曲线面积S;而对于变荷载动态试验,总循环次数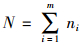
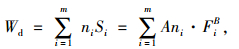
|
(11) |
式中,Fi(i=1, 2, …, m)为不同的荷载级位; ni(i=1, 2, …, m)为荷载级位Fi的作用次数。由此可以得到变荷载情况下4种混合料的累积耗散能预测方程,其A, B参数见表 3。
| 混合料类型 | A | B | R2 |
| SBS35 | 9.267 4 | 2.034 0 | 0.999 3 |
| SBS55 | 9.168 0 | 2.052 5 | 0.999 6 |
| 70#35 | 9.577 7 | 2.099 1 | 0.999 7 |
| 70#55 | 9.224 7 | 2.071 2 | 0.999 1 |
3.2.3 基于累积耗散能的疲劳方程
不妨用混合料的疲劳寿命Nf来描述其荷载状态ni和Fi,根据式(11) 可以得到累积耗散能表示的4种混合料疲劳方程见表 4。
| 混合料类型 | 疲劳方程 |
| SBS35 | lg Wd=0.967 0+2.034 0lg Nf |
| SBS55 | lg Wd=0.962 3+2.052 5lg Nf |
| 70#35 | lg Wd=0.981 2+2.099 1lg Nf |
| 70#55 | lg Wd=0.965 0+2.071 2lg Nf |
表 4推得的疲劳方程说明SBS改性沥青耐疲劳性能优于70#基质沥青,调高级配通过率有助于提高混合料耐疲劳性能。另一方面,基于累积耗散能的疲劳方程表达形式与一般的双对数疲劳方程完全相同,其特点在于:
(1) 考虑了变载情况对混合料疲劳寿命的影响,更符合路面结构的实际受力情况;
(2) 通过滞回曲线形态参数的研究可以对材料的疲劳特性进行预估。
4 结论基于黏弹理论,确立了沥青混合料动态抗压回弹模量滞回曲线的形态参数k,e,S,通过不同试验条件下的形态参数对混合料的力学特性进行研究,得到以下结论:
(1) 形态参数k,e,S分别表征混合料的模量、黏滞性和耐疲劳性,且对荷载、温度、级配组成等影响因素具有较高的敏感性,可以借助滞回曲线形态参数对材料的力学性能进行研究;
(2) 建立了回弹模量的应力依赖模型,其拟合值与实测代表值相关性良好;
(3) 通过稳态耗散能的幂函数模型建立了累积耗散能的预测方程,并由此建立了疲劳方程,有助于对材料疲劳特性的研究。
| [1] | 刘璐, 黄小坤, 田春雨, 等. 配置大直径大间距HRB500高强钢筋的装配整体式钢筋混凝土框架节点抗震性能试验研究[J]. 建筑结构学报, 2016, 37(5): 247-254 LIU Lu, HUANG Xiao-kun, TIAN Chun-yu, et al. Experimental Study on Seismic Performance of Precast RC Frame Joints with HRB500 High Strength Rebars of Large Diameter and Spacing[J]. Journal of Building Structures, 2016, 37(5): 247-254 |
| [2] | 陈世鸣, 庄炳芮, 周祖岳. O-Stable Panel装配整体式墙板抗震性能试验研究[J]. 工程力学, 2016, 33(5): 176-183 CHEN Shi-ming, ZHUANG Bing-rui, ZHOU Zu-yue. Seismic Performance Evaluation of Assembled O-stable Panel Walls[J]. Engineering Mechanics, 2016, 33(5): 176-183 |
| [3] | 罗飞, 赵淑萍, 马巍, 等. 青藏冻结黏土滞回曲线形态特征的定量研究[J]. 岩石力学与工程学报, 2013, 32(1): 208-215 LUO Fei, ZHAO Shu-ping, MA Wei, et al. Quantitative Research on Morphological Characteristics of Hysteretic Curves of Qinghai-Tibet Frozen Clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(1): 208-215 |
| [4] | 张媛, 许江, 杨红伟, 等. 循环荷载作用下围压对砂岩滞回环演化规律的影响[J]. 岩石力学与工程学报, 2011, 30(2): 320-326 ZHANG Yuan, XU Jiang, YANG Hong-wei, et al. Effect of Confining Pressure on Evolution Law of Hysteresis Loop of Sandstone under Cyclic Loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 320-326 |
| [5] | 李源. 疲劳耗散能及其在疲劳性能快速预测中的应用研究[D]. 长沙: 湖南大学, 2013. LI Yuan. Study on Fatigue Dissipated Energy and Its Application in Rapid Prediction of Fatigue Properties[D]. Changsha:Hunan University, 2013. |
| [6] | 雷冬, 赵建华, 龚明, 等. 疲劳过程中的能量耗散和疲劳寿命的预测[J]. 实验力学, 2008, 23(5): 432-442 LEI Dong, ZHAO Jian-hua, GONG Ming, et al. On the Energy Dissipation in Fatigue Process and Fatigue Life Prediction[J]. Journal of Experimental Mechanics, 2008, 23(5): 432-442 |
| [7] | 詹小丽. 基于DMA方法对沥青黏弹性能的研究[D]. 哈尔滨: 哈尔滨工业大学, 2007. ZHAN Xiao-li. Research on Viscoelastic Properties of Asphalt Using DMA[D]. Harbin:Harbin Institute of Technology, 2007. |
| [8] | 尹应梅. 基于DMA法的沥青混合料动态黏弹特性及剪切模量预估方法研究[D]. 广州: 华南理工大学, 2010. YIN Ying-mei. Research on Dynamic Viscoelastic Characteristics and Shear Modulus Predicting Methods for Asphalt Mixtures Based on Dynamic Mechanical Analysis (DMA) Means[D]. Guangzhou:South China University of Technology, 2010. |
| [9] | 崔新壮, 金青, 张娜, 等. 损伤沥青混合料渗透性模型与水稳定性试验[J]. 中国公路学报, 2014, 27(3): 1-10 CUI Xin-zhuang, JIN Qing, ZHANG Na, et al. Experiment on Permeability Model and Water Stability of Damaged Asphalt Mixture[J]. China Journal of Highway and Transport, 2014, 27(3): 1-10 |
| [10] | WITCZAK M W, KALOUSH K, PELLINEN T, et al. Simple Permance Test for Superpave Mix Design[M]. Washington, D. C.: Transportation Research Board, 2002. |
| [11] | KHOURY N, BROOKS R, KHOURY C, et al. Modeling Resilient Modulus Hysteretic Behavior with Moisture Variation[J]. International Journal of Geomechanics, 2012, 12(5): 519-527 |
| [12] | 陈剑, 苏跃宏. 交通荷载作用下公路路基动力特性的数值模拟研究[J]. 公路交通科技, 2011, 28(5): 44-48 CHEN Jian, SU Yue-hong. Numerical Simulation of Dynamic Performance of Highway Subgrade under Traffic Loads[J]. Journal of Highway and Transportation Research and Development, 2011, 28(5): 44-48 |
| [13] | 马士杰, 付建村, 韦金城, 等. 大粒径透水性沥青混合料动态模量预估模型研究[J]. 公路交通科技, 2010, 27(5): 36-40, 46 MA Shi-jie, FU Jian-cun, WEI Jin-cheng, et al. Study on Dynamic Modulus Prediction Model of Large Stone Porous Asphalt Mixture[J]. Journal of Highway and Transportation Research and Development, 2010, 27(5): 36-40, 46 |
| [14] | 张蓓, 刘强, 钟燕辉, 等. FWD荷载作用下刚性路面弯沉的动力响应分析[J]. 公路交通科技, 2009, 26(7): 36-37 ZHANG Bei, LIU Qiang, ZHONG Yan-hui, et al. Analysis of Dynamic Response of Rigid Pavement Deflection under FWD Load[J]. Journal of Highway and Transportation Research and Development, 2009, 26(7): 36-37 |
| [15] | 徐志荣, 常艳婷, 陈忠达, 等. 沥青混合料动态模量试验标准研究[J]. 交通运输工程学报, 2015, 15(3): 1-8 XU Zhi-rong, CHANG Yan-ting, CHEN Zhong-da, et al. Study on Test Standard of Asphalt Mixture Dynamic Modulus[J]. Journal of Traffic and Transportation Engineering, 2015, 15(3): 1-8 |
| [16] | 孙建. 沥青混合料动态模量研究[D]. 西安: 长安大学, 2006. SUN Jian. Study on Dynamic Modulus of Asphalt Mixtures[D].Xi'an:Chang'an University, 2006. |
| [17] | 羊明. 沥青混合料动态模量研究[D]. 长沙: 长沙理工大学, 2007. YANG Ming. Research on Dynamic Modulus of Asphalt Mixtures[D]. Changsha:Changsha University of Science and Technology, 2007. |
| [18] | 姚爱玲, 张西玲, 王选仓. 测试方法对沥青混合料抗压回弹模量的影响[J]. 长安大学学报:自然科学版, 2005, 25(6): 21-24 YAO Ai-ling, ZHANG Xi-ling, WANG Xuan-cang. Affect of Test Methods on Compression Module of Asphalt Mixture[J]. Journal of Chang'an University:Natural Science Edition, 2005, 25(6): 21-24 |
 2017, Vol. 34
2017, Vol. 34
