扩展功能
文章信息
- 焦志强, 靳文舟, 郝小妮
- JIAO Zhi-qiang, JIN Wen-zhou, HAO Xiao-ni
- 综合效益最优的路边停车价格研究
- Study on Curbside Parking Price Based on Optimal Comprehensive Benefit
- 公路交通科技, 2017, 34(9): 109-115
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(9): 109-115
- 10.3969/j.issn.1002-0268.2017.09.015
-
文章历史
- 收稿日期: 2016-07-05
在城市中心区域,道路资源有限、交通流量大且路边停车位长期处于饱和状态,而路边停车巡游车辆又加剧了整个区域的交通拥堵,因此,城市中心区停车问题研究尤为迫切。路外停车场在固定的空间位置上提供大量的停车位,但由于目前缺乏合理有效的路边停车收费策略,在路外停车场和路边停车位存在相互竞争的区域,往往出现路边停车位供不应求,而附近路外停车场大量车位空闲(节假日等特殊时间路内与路边车位均供不应求的情况除外)。根据Shoup等[1-2]的研究,一些城市中心区因寻找路边停车位而产生的巡游交通量可达路段交通流量的30%。停车者寻找停车位而额外增加的出行时间增加了路边停车者的广义成本;因巡游而产生的交通量增加了通过性车辆的通行时间,且加剧了交通拥堵。因而研究制订合理的路边停车收费策略,对于提高路外停车场的利用率、减少路内巡游车辆、缓解城市交通拥堵具有十分重要的意义。
笔者根据停车设施类型的不同,将停车收费分为路边停车收费和路外停车场停车收费。目前各城市管理部门及学者在研究制订停车费率时, 往往将这两类停车设施分开单独考虑。国外方面,一些研究认为路边停车是相对独立的[3-4],然而实际情况下, 这两类停车设施是相互影响的, 停车收费策略会影响停车者的停车方式选择, 进而对该范围内其他车辆的运行产生影响, 最终影响整个系统的效益。例如:提高路外停车场的停车收费费率,则会有更多的停车者选择路边停车,路边停车者需要更多的巡游时间搜寻路边停车位,路边停车者巡游成本增加的同时,通过性车辆的延误成本也会增加,进而产生更多的负外部成本。另外一些研究虽然把路边停车与路外停车场停车同时考虑,但忽略了停车者停放时间的不同[5-6]。A.Glazer和E.Calthrop等[7-8]考虑到了停车者之间停放时间的差异;R.Arnott等[9]在此基础上增加了停放时间的限制;S.P.Anderson等[10]研究了路边停车与路外停车场停车之间的竞争,但他们均忽略了不同停放时间下停车收费费率之间的差异。E.Inci等[11]考虑到了随停放时间而变化的停车费率;M.B.W.Koubs等[12]对路内停车位溢价状态下停车者停车位置选择问题进行了研究;H.Lin等[13]研究了路内停车位与路外停车场之间的竞争关系和存在的价格歧视问题,但都忽略了路边停车巡游车辆给过境交通流带来的延误。国内方面,安实等[14]提出了路边停车收费的双层规划模型;梅振宇等[15]研究了基于停车选择行为的路内停车定价方法;范文博等[16]提出了用户均衡条件下3类停车设施收费定价模型,但以上研究都未考虑到路边停车收费费率随停放时间的变化。
国内外以上停车收费研究文献,未同时考虑存在巡游车辆时通过性车辆的延误成本和随停放时间变化的停车收费费率。实际上,巡游车辆所引起的通过性车辆延误成本占停车系统总成本相当大的比例,且巡游车辆数量对停车者的停车方式选择也有显著影响。笔者将主要研究市中心路边停车和路外停车场停车存在相互竞争、存在大量巡游车辆区域内的停车方式选择问题,在详细分析路边停车和路外停车场停车相互竞争的基础上,探讨对路边停车位如何制订合理的停车收费策略,以控制巡游交通量、减轻交通拥堵、提高路外停车场的使用率,进而达到综合效益最优的效果。
1 模型建立 1.1 问题描述如图 1所示,市中心1条道路旁有路外停车场A和B及路边停车区域,图中线段长短不代表实际值,各参数具体值及相对大小以实际应用中的计算结果为准。停车者的目的地位于道路两侧区域。单位时间内有若干数量的车辆需通过此区域,称之为过境交通流。有若干数量车辆的目的地位于此区域,此类车辆需要在附近以路边停车或停车场停车的方式停靠,称之为停靠交通流。不失一般性,本研究中每个停车者均为理性经济人,依据个人停车总费用最小原则选择停车方式。笔者拟在路外私人运营停车场停车定价既定的条件下,基于停车者停车方式选择均衡模型,以综合效益最优为最终目标,提出一个新的路边停车收费定价模型。

|
| 图 1 研究区域示意图 Fig. 1 Schematic diagram of study area |
| |
1.2 基本假设
现提出以下几个基本假设:
(1) 单位时间内总的停车需求是固定的。
(2) 停车者的目的地均匀地分布在道路两侧。
(3) 单位时间内的过境交通量是固定的(即使因巡游交通量产生了交通拥堵)。
(4) 停放时间分为两大类:短时间停放和长时间停放。
(5) 路边停车的驾驶员距离目的地的步行距离很小,可以忽略不计。
(6) 停车者均熟悉路外停车场的位置,选择路外停车场停车时的搜索成本为零。
(7) 系统运行状态稳定,毗邻的路外停车场收费价格相同。
1.3 系统成本分析与停车巡游成本和因此产生的通过性车辆延误成本相比,路边停车位的运营维护成本相对小很多,因此忽略路边停车位的运营成本。由此,当停车总需求固定时,停车系统总成本包括路外停车场的运营成本、路外停车场停车者至目的地的步行成本、路边停车者的停车位搜索成本、巡游车辆引起的通过性车辆的延误成本4项。路外停车场的运营成本包括人力成本、车位维护费、保险费和税费等;步行成本取决于路外停车场与目的地间的步行距离及停车者的时间价值;路边停车位搜索成本、通过性车辆的延误成本均与巡游车辆数量及实际道路条件密切相关。
以综合效益最优为最终目标,即研究范围内的停车系统总费用最小。总费用则主要取决于选择路边停车和路外停车场停车的车辆数量,由于停车场A和B两侧情况相同,只需研究图 1所示范围内停车系统的总费用即可。
1.3.1 路外停车场运营成本路外停车场的运营维护成本随停车数量的增加而变大,设路外停车场每车单位时间内停车运营成本为α[17],则停车场A和B之间需要长时间停车和短时间停车的车辆数目分别为2dcxc,2ddxd,则图 1所示范围内路外停车场A和B所需的运营成本GC为:
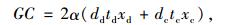
|
(1) |
式中,dd和dc分别为路外停车场A和B间短时间停车者和长时间停车者目的地的分布密度;td和tc分别为短时间停放车辆和长时间停放车辆的停车时长;xd和xc分别为选择路外停车场的停车者短时间停车和长时间停车目的地距离所选路外停车场的最远距离。
由于笔者旨在对路边停车收费的定价方法进行说明,故本研究暂将停车时间简化为两大类停车时长,实际应用中,停车时长分类和具体界定数值可根据研究区域内的车辆停放特征调查结果而定。
路外停车场停车和路边停车收费的最大不同之处在于收费方式不同,目前很多城市路边停车收费一般采用固定费率通过咪表收费,路外停车场则为了达到经营利润的最大化,针对不同停放时长的停车者制订了不同的费率,但是,为使研究区域内不同停车设施间的停放车辆分布更加均衡、合理,且把巡游车流量控制在一定的范围之内,假定路边停车收费的费率是可以变化的,对不同停车时长的车辆依据不同停车费率收费。
1.3.2 路外停车场停车者的步行成本假定路边停车者总是优先选择靠近目的地的车位停车,因此认为路边停车者的步行成本为零。
路外停车场停车者至目的地的步行成本WC为:

|
(2) |
式中,Wd和Wc分别为路外停车场停车的短时间停车和长时间停车者单位距离的步行成本;x为被积函数; xc≤D/2, xd≤D/2, D为毗邻的路外停车场A和B之间的距离。
1.3.3 路边停车位搜索成本假定停车者熟悉该研究区域内路外停车场的位置,选择路外停车场的停车者可直接行驶至停车场,则搜索成本为零。当路边停车位紧缺、系统处于稳定状态时,选择路边停车的车辆均需要一定搜索时间。

|
(3) |

|
(4) |
式中,Nc为此时系统内总的巡游车辆数;T为总的路边停车位占用车时。
结合E.Inci等人的研究,笔者认为在路边停车位紧缺的市中心区域,两类停车者路边停车的搜索成本与路边停车位的总占用车时T成正比,比例系数分别为kd和kc[11],即路边停车的车辆中共有dd(D-2xd)个短时间停车的停车者,dc(D-2xc)个长时间停车的停车者,两类停车者的搜索成本分别为kdT和kcT。路边停车者停车所需的总搜索成本SC为:

|
(5) |
式中,xc≤D/2,xd≤D/2。
1.3.4 通过性车辆的延误成本路边停车的车辆在搜索停车位的巡游过程中,加剧了道路的拥堵程度[18],增大了通过性车辆的通行时间[19],结合R.Arnott[6]、孙镠阳等[20]的研究,笔者认为一辆巡游的车辆对交通流产生的影响相当于一辆通过性车辆的θ倍[3], 则在巡游车辆的影响下,有:

|
(6) |

|
(7) |
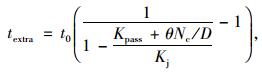
|
(8) |
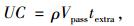
|
(9) |
式中,t1为在巡游车辆的影响下通过性车辆通过A和B所需的时间;t0为车辆以畅行速度通过A和B所需的时间;textra为停车巡游车辆造成的通过性车辆的延误时间;Kpass为通过性车辆的平均车流密度;Kj为A和B间车辆的阻塞密度;θ为巡游交通量与通过性交通量的折算系数;Vpass为单位时间内A和B间的过境交通量;UC为通过性车辆的延误成本;ρ为通过性车辆的单位时间成本。
1.4 停车方式选择均衡模型均衡条件下,到路外停车场距离为xd和xc的临界位置处,长时间停车和短时间停车的停车者选择路边停车或路外停车场停车的总费用总是相同的,即停车者无法通过改变停车方式去降低自己的停车费用。

|
(10) |
式中,Pcd和Pcc分别为路边短时间停车和长时间停车的收费费率;Pgd和Pgc分别为路外停车场短时间停车和长时间停车的收费费率;Pgctc+Wcxc,Pcctc+ kcT,Pgdtd+Wdxd,Pcdtd+kdT分别为临界位置处,路外停车场长时间停车者、路边长时间停车者、路外停车场短时间停车者、路边短时间停车者的停车总费用。
一般而言,随着停车时长的增加,路外停车场单位时间内的收费逐步降低,路边停车位为达到提高路边泊位周转率的目的,制订的收费价格会不利于长时间的路边停车。但是长时间停车的总费用是大于短时间停车的,否则会出现短时间的停车者为减少停车花费而故意延长停车时长的情况,所以参数间有以下关系:Pcdtd < Pcctc,Pgdtd<Pgctc。
1.5 路边停车收费定价模型将式(1), (2), (5), (9) 相加可得到图 1停车系统的总成本TC,综合效益最优即对应停车系统总花费最小,建立模型如下。
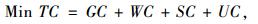
|
(11) |

|
(12) |
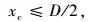
|
(13) |
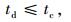
|
(14) |
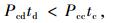
|
(15) |
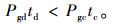
|
(16) |
对式(11) 求一阶偏导,结果如下。
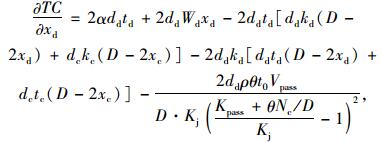
|
(17) |
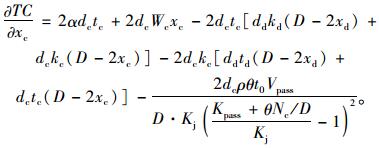
|
(18) |
Frank-Wolfe算法是针对线性约束优化问题提出来的,一般形式为[21]:
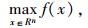
|
(19) |
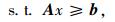
|
(20) |
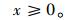
|
(21) |
该算法针对上述形式问题设计线性逼近方法,式中x为函数自变量;f(x)为n维实数集Rn上的非线性光滑函数;A为约束方程的系数矩阵;b为列向量,且A∈Rm×n, b∈Rm,Rm×n为m×n阶实数矩阵,m和n均为实数。
算法的具体思路如下。
记Q={Ax≥b, x≥0},Q表示可行解集合,任取x0∈Q,在x0处目标函数f(x)的线性逼近函数为:
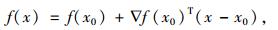
|
(22) |
式中

分两种情况讨论最初问题的最优解,本研究不在此赘述,更加详细的计算说明及收敛性的证明见文献[22]。
(1) 若∇f(x0)(x-x0)=0,则x0为原问题的KT点。
(2) 若∇f(x0)(x-x0)≠0,则方向d=y0-x0为原问题的可行下降方向,沿着这个方向进行精确线性搜索,即是求解单变量λ的极值问题:

|
(23) |
得到最优解λ0后,令x1=x0+λ0(y0-x0),x1为x0与Q的顶点y0连线上的最优解,且
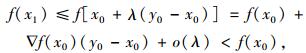
|
(24) |
式中o(λ)为λ的高阶无穷小。
得到x1后,再次应用线性逼近,重复以上步骤即可。
本研究运用MATLAB软件结合Frank-Wolfe算法进行优化模型求解的算法流程如图 2所示,其中xk为算法第k次迭代后得到的可行点;yk为第k次迭代后所得最优解;λk为第k次迭代后得到的步长因子;ε为算法判断准则中的精确度。

|
| 图 2 模型算法流程图 Fig. 2 Flowchart of model algorithm |
| |
具体算法步骤如下。
Step 1:运用MATLAB,根据一阶条件∂TC/∂xd=0,∂TC/∂xc=0,得出xd和xc关于变量α,dd,dc,td,tc,Kj,Vpass,Kpass,θ,ρ,t0,D,kd,kc的函数表达式。
Step 2:根据实际调研,在相关参数确定的条件下,求得xd,xc。
Step 3:由Step 2中所得的xd和xc验证二阶条件∂2TC/∂xd>0、∂2TC/∂xc>0,若通过验证,则确定xd和xc为TC的最小值点,进行Step 7;若未通过验证,则进行Step 4。
Step 4:运用Frank-Wolfe算法对模型进行求解,给定初始可行点x1=(D/2,D/2), 允许误差ε>0,置k=1。
Step 5:求解线性规划问题
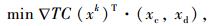
|
(25) |
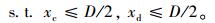
|
(26) |
得到最优解yk, 若|TC(xk)T(yk-xk)|≤ε, 则停止计算,否则进行Step 6。
Step 6:从xk出发,沿方向yk-xk在连接xk和yk的线段上搜索:

|
(27) |
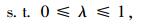
|
(28) |
得到λk。
令xk+1=xk+λk(yk-xk),置k=k+1,返回Step 5。
Step 7:将求得的xd和xc结果代入式(10) 即可得到Pcc和Pcd,进而得到TC。
2 算例 2.1 模型参数条件以广州市中心某区域为例,道路D两旁允许路边停车,停车场A和B为地下停车库,如图 3所示。道路为双向六车道,道路两旁可供路边停车,此区域工作日期间固定时段通过性交通流量基本保持恒定,道路D两侧商业区域为停车者目的地,路边停车位长期处于饱和状态。

|
| 图 3 实际算例区位 Fig. 3 Location of practical calculation example |
| |
结合实地调研结果及假设,具体模型参数值如下: D=950 m,α=5元/(veh·h),dd=100 /km,dc=80 /km,Wd=50元/km,Wc=40元/km,t0=2 min,td=1 h,tc=2 h,ρ=50元/h,θ=1.3,kd=0.16,kc=0.16,Vpass=1 800 veh/h,Kpass=120 veh/km,Kj=375 veh/km,Pgc=12元/h,Pgd=8元/h。其中Kj,Vpass,Kpass为单方向的大小。
2.2 算例结果与分析求解算例,不考虑停车巡游车辆对过境交通流的影响时,xd=257 m,xc=390 m;考虑停车巡游车辆对过境交通流的影响时,xd=379 m,xc=402 m。得到的停车场最优定价策略与设施间停车流分担情况如表 1所示。
| 是否考虑通过性车辆的延误成本 | 路边长时间停车收费定价/(元·h-1) | 路边短时间停车收费定价/(元·h-1) | 路边停车流量分担率/% | 通过性车辆的延误成本/元 | 系统总成本/元 |
| 不考虑 | 10.1 | 13.5 | 33.5 | 3 369.4 | 5 715.3 |
| 考虑 | 12.4 | 22.9 | 14.9 | 2 109.0 | 4 641.0 |
| 变化幅度/% | +22.8 | +69.6 | -55.2 | -37.4 | -18.8 |
由表 1可见,传统方法忽略路边停车巡游车辆给过境交通流带来的延误成本,导致了较低的路边停车定价、较低的路外停车场停车需求分担率、较高的过境交通流延误成本、较高的系统总成本。而根据考虑通过性车辆延误成本后所建优化模型求解结果,重新设置的路边停车收费定价有效地降低了停车系统的总成本,降幅达18.8%,通过性车辆的延误减少了37.4%,路边停车位停车需求分担率减少了55.2%。其次,路边短时间停车收费定价涨幅远大于路边长时间停车收费定价涨幅,原因在于路边短时间停车者对停车收费定价的敏感性较弱,从而促使这类停车者转变为选择路外停车的难度也较大。另外,选择临近路外停车场的路边停车位和旁边路外停车场停车之间,步行距离差别很小,此时,停车者偏向于选择费率明显较低的路外停车场,即临近路外停车场的路边停车位相对于旁边路外停车场停车竞争力较弱,因此接近路外停车场的一定范围内不宜设置路边停车位,以免造成资源浪费。
3 结论以综合效益最优为目标,在路外停车场停车收费定价既定的情况下,探讨了路边停车收费的最优化定价问题。首先建立了基于停车者停车方式选择均衡模型,模拟停车者以个体总费用最小为原则的停车设施选择行为。其次以综合效益最优为目标,建立了基于停车方式选择的路边停车收费定价模型。结果表明,研究范围内系统总成本由原来的5 715.3元降低到4 641.0元,降幅为18.8%,可有效降低系统的总花费。路外停车场的停车分担率由原来的66.5%增长为85.1%,可有效提高路外停车场的利用率,减少路内巡游交通量。通过性车辆的延误成本由原来的3 369.4元降低到2 109.0元,降幅达37.4%,效果显著。
在很多城市中心区,路边停车位供不应求,而路外停车场存在大量空闲泊位,造成资源浪费的同时,较多的路内停车巡游车辆也加剧了交通拥堵。在停车管理的过程中,应考虑到路边停车巡游车辆带来的通过性车辆的延误成本,适当提高路边停车收费定价,以提高路外停车场的停车需求分担率,使不同停车设施间停放车辆的分布更加均衡,最终达到综合总体效益最优的效果。
| [1] | SHOUP D C. The High Cost of Free Parking[J]. Journal of Planning Education & Research, 2005, 17(1): 3-20 |
| [2] | SHOUP D C. Cruising for Parking[J]. Transport Policy, 2006, 13(6): 479-486 |
| [3] | ARNOTT R, INCI E. An Integrated Model of Downtown Parking and Traffic Congestion[J]. Journal of Urban Economics, 2006, 60(3): 418-442 |
| [4] | ARNOTT R, INCI E. The Stability of Downtown Parking and Traffic Congestion[J]. Journal of Urban Economics, 2010, 68(3): 260-276 |
| [5] | ARNOTT R, ROWSE J. Downtown Parking in Auto City[J]. Regional Science and Urban Economics, 2009, 39(1): 1-14 |
| [6] | ARNOTT R, INCI E, ROWSE J. Downtown Curbside Parking Capacity[J]. Journal of Urban Economics, 2015, 86: 83-97 |
| [7] | GLAZER A, NISKANEN E. Parking Fees and Congestion[J]. Regional Science & Urban Economics, 1992, 22(1): 123-132 |
| [8] | CALTHROP E, PROOST S. Regulating On-street Parking[J]. Regional Science & Urban Economics, 2006, 36(1): 29-48 |
| [9] | ARNOTT R, ROWSE J. Curbside Parking Time Limits[J]. Transportation Research Part A:Policy & Practice, 2013, 55: 89-110 |
| [10] | ANDERSON S P, PALMA A D. Parking in the City[J]. Papers in Regional Science, 2007, 86(4): 621-632 |
| [11] | INCI E, LINDSEY R. Garage and Curbside Parking Competition with Search Congestion[J]. Regional Science & Urban Economics, 2015, 54: 49-59 |
| [12] | KOBUS M B W, GUTIÉRREZ-I-PUIGARNAU E, RIETVELD P, et al. The On-street Parking Premium and Car Drivers' Choice between Street and Garage Parking[J]. Regional Science & Urban Economics, 2013, 43(2): 395-403 |
| [13] | LIN H, WANG I Y. Competition and Price Discrimination:Evidence from the Parking Garage Industry[J]. Journal of Industrial Economics, 2015, 63(3): 522-548 |
| [14] | 安实, 王健. 企业管理模式下的中国城市路边停车定价方法与应用研究[J]. 中国公路学报, 2002, 15(2): 113-116 AN Shi, WANG Jian. Study of Curb Parking Pricing of Corporation Management-mode in China[J]. China Journal of Highway and Transport, 2002, 15(2): 113-116 |
| [15] | 梅振宇, 项贻强, 陈峻, 等. 基于停车选择行为的路内停车价格优化模型[J]. 交通运输系统工程与信息, 2010, 10(1): 99-104 MEI Zhen-yu, XIANG Yi-qiang, CHEN Jun, et al. Optimizing Model of Curb Parking Pricing Based on Parking Choice Behavior[J]. Journal of Transportation Systems Engineering and Information Technology, 2010, 10(1): 99-104 |
| [16] | 范文博. 用户均衡条件下3类停车设施收费定价模型[J]. 重庆交通大学学报:自然科学版, 2013, 32(4): 656-658 FAN Wen-bo. Pricing Model of Three-class Parking Facilities under User Equilibrium Conditions[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2013, 32(4): 656-658 |
| [17] | ANDERSON S P, PALMA A D. The Economics of Pricing Parking[J]. Journal of Urban Economics, 2004, 55(1): 1-20 |
| [18] | 苏岳龙, 路鹭, 姚丹亚, 等. 经典交通流模型在城市车路不均衡发展评价中的应用[J]. 公路交通科技, 2010, 27(11): 108-112 SU Yue-long, LU Lu, YAO Dan-ya, et al. Evaluation of Imbalanced Development between Vehicles and Urban Road Using Classical Traffic Flow Model[J]. Journal of Highway and Transportation Research and Development, 2010, 27(11): 108-112 |
| [19] | 李艳红, 袁振洲, 靳雄焕. 基于自由流时间的交通拥挤收费费率研究[J]. 公路交通科技, 2009, 26(6): 109-113 LI Yan-hong, YUAN Zhen-zhou, JIN Xiong-huan. Research on Traffic Congestion Tolling Rate Based on Free Flow Time[J]. Journal of Highway and Transportation Research and Development, 2009, 26(6): 109-113 |
| [20] | 孙镠阳. 基于路内停车巡游的停车收费策略研究[D]. 成都: 西南交通大学, 2015. SUN Liu-yang. Research on Parking Charge Strategy Based on Cruising for On-street Parking[D]. Chengdu:Southwest Jiaotong University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10613-1015340398.htm |
| [21] | 张美芳. 改进的求解线性多层规划的主元标单纯形法[D]. 湘潭: 湘潭大学, 2009. ZHANG Mei-fang. An Improved Pivot Simplex Method for Multilevel Linear Programming[D]. Xiangtan:Xiangtan University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10530-2010012621.htm |
| [22] | 陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 1989. CHEN Bao-lin. Optimization Theory and Algorithm[M]. Beijing: Tsinghua University Press, 1989. |
 2017, Vol. 34
2017, Vol. 34
