扩展功能
文章信息
- 刘扬, 周志彬, 张海萍
- LIU Yang, ZHOU Zhi-bin, ZHANG Hai-ping
- 基于支持向量回归的桥梁抗震动力可靠度计算
- Calculation of Seismic Dynamic Reliability of Bridges Based on Support Vector Regression
- 公路交通科技, 2017, 34(9): 86-92
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(9): 86-92
- 10.3969/j.issn.1002-0268.2017.09.012
-
文章历史
- 收稿日期: 2016-10-25
近年来,基于性能的结构抗震设计理论得到深入发展,对桥梁结构进行抗震可靠度分析的需求日益增加[1]。确定性结构在随机地震动激励作用下的可靠度分析方法已经逐渐成熟[2-7]。但实际工程本身的结构参数也具有一定随机性,这些随机因素包括几何尺寸、材料参数等会对结构动力可靠度分析产生较大影响[8]。因此,同时考虑结构参数随机性和地震动激励随机性的桥梁结构动力可靠度分析具有重要的研究价值。
在考虑双重随机性的结构可靠度分析研究中,陈建兵、李杰提出了随机结构复合随机振动分析的概率密度演化方法[9],通过引入扩展状态变量,构造具有随机初始条件的状态方程,导出了复合随机振动反应的概率密度演化方程。陈颖等[10]基于神经网络响应面法建立了结构随机参数与响应特征值的映射关系,再建立功能函数通过一次二阶矩法得到可靠指标。贾布裕等[11]通过将地震激励离散成一列随机变量作为输入训练Kriging模型,再结合MC法计算得到结构可靠指标。
为了计算在结构参数随机性与地震动激励随机性的耦合作用下桥梁结构的抗震动力可靠度,先不考虑结构参数随机性,计算出确定结构在随机地震作用下的失效概率;再考虑结构参数与失效概率的关系,利用全概率公式得出结构在双重随机性下的可靠度。并结合工程背景说明该方法的具体应用,结果表明该方法具有较高的计算效率。
1 理论基础 1.1 基于首次超越的结构破坏准则首超破坏理论是工程结构可靠度分析中经常采用的一种方法。该理论认为结构的破坏以响应值X(t)首次超过某一限值b为标志,则结构在时间T内的可靠概率为:
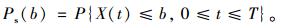
|
(1) |
随机过程X(t)在时间T内与某一限值b交叉次数的期望值Nb(T)可表示为:

|
(2) |
式中vb(t)为单位时间内的交叉次数。设X(t)与
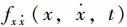
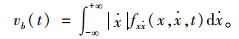
|
(3) |
Rice[12]给出了零均值平稳正态随机响应的界限跨越概率:
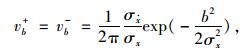
|
(4) |
式中σx,
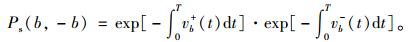
|
(5) |
结构响应为零均值的平稳高斯过程时,将式(4) 代入式(5) 可得结构的动力可靠概率为:
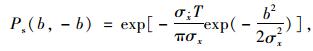
|
(6) |
则失效概率:
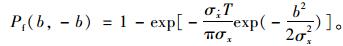
|
(7) |
近年来,支持向量机(Support Vector Machine,SVM)成为人工智能研究的新热点[13],并已经在结构可靠度计算中得到应用[14]。SVM是建立在结构风险最小原理(SRM)基础上的,能很好地处理小样本问题和高度非线性问题,并且从原理上保证是全局最优解。文献[15]比较了以径向基函数(RBF)为核函数的SVM方法和神经网络方法,说明了SVM在小样本数据下具有更高的优势。SVM的思想是Vapnik在1963年提出的,用以解决模式识别问题。1995年Vapnik系统地提出了统计学习理论,使SVM得以广泛应用于模式识别、回归分析等问题中。支持向量回归(SVR)是SVM的一种应用,下面介绍SVR的基本原理。
给定训练集T={(x1, y1), …, (xi, yi), …, (xl, yl)}, xi∈Rn, yi∈R, l为训练集的数量。对于线性回归问题,用函数f(x)=wx+b拟合实际映射,式中向量w和截距b控制超平面位置。考虑到训练数据可能存在误差或者有离群值,为避免这些不正常的数据影响SVR模型,引入损失量ξi, ξi*≥0,对应于数据(xi, yi)的左右偏离量。把损失加入到目标函数中,至此得到目标函数:
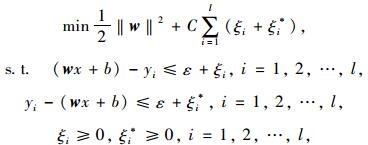
|
(8) |
式中C为损失函数(Loss Function)的权因子,用于控制目标函数中两项(模型复杂程度和数据点偏差量)之间的权重。ε为松弛因子(Slack Variable),用以去除数据噪音,数据预测误差小于ε的部分将会被忽略。对于非线性回归问题,可以通过引入核函数将非线性问题变换为线性问题。再通过运用Lagrange乘子和对偶原理,将约束写入目标函数可得式(8) 的对偶问题:
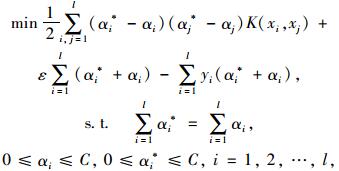
|
(9) |
求解此优化问题,得回归函数为:
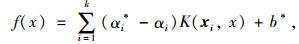
|
(10) |
式中,αi*,αi为Lagrange因子;K(xi, xj)为核函数。常用的核函数有:线性核函数K(xi, xj)=xiTxj,多项式核函数K(xi, xj)=(γxiTxj+r)d,高斯核函数K(xi, xj)=exp(-γ‖xi-xj‖2)等,γ>0。高斯核函数是一种径向基函数在可靠度分析中常常被用到,因为这种核函数通过调整γ值将会有很高的灵活性,可以将原始空间映射到无穷维。如果γ选得过小,高次特征的权重将会衰减得很快,数值上近似于一个低维子空间;如果γ选得很大,则可以将任意数据精确拟合,但这将会带来严重的过拟合现象。由于C和γ是影响模型的重要因素,所以在训练SVR模型时,需要找到最优的C和γ。一般基于交叉验证SVR参数寻优方法有网格法、粒子群算法、遗传算法等。
2 桥梁抗震可靠性分析方法 2.1 确定性结构抗震可靠度计算基于首超破坏理论计算结构可靠度的前提是计算结构在荷载作用下关键截面的动力响应(应力、位移等)的均方差σxi 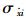
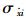
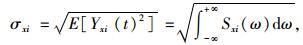
|
(11) |
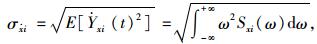
|
(12) |
进而根据式(7) 可得确定性结构在随机地震动激励下的失效概率Pfi。
2.2 建立SVR模型为了计算考虑结构参数随机性和地震动激励随机性的复合随机系统的失效概率,在上述分析方法的基础之上,还需要增加对结构参数随机性的考虑。先确定m组结构参数X1(x11, x21, …, xn1), X2(x12, x22, …, xn2), …, Xm(x1m, x2m, …, xnm),再逐次修改有限元模型并进行功率谱密度分析,计算出第i组结构参数Xi对应的结构失效概率Pfi。
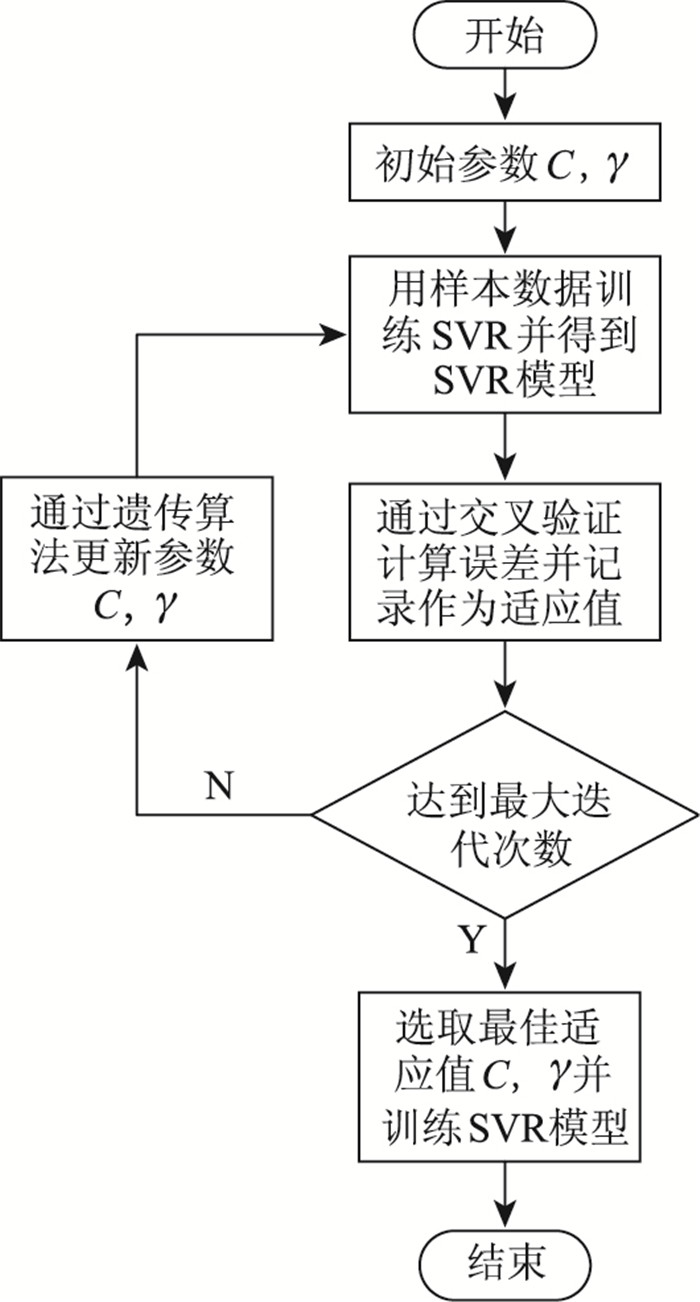
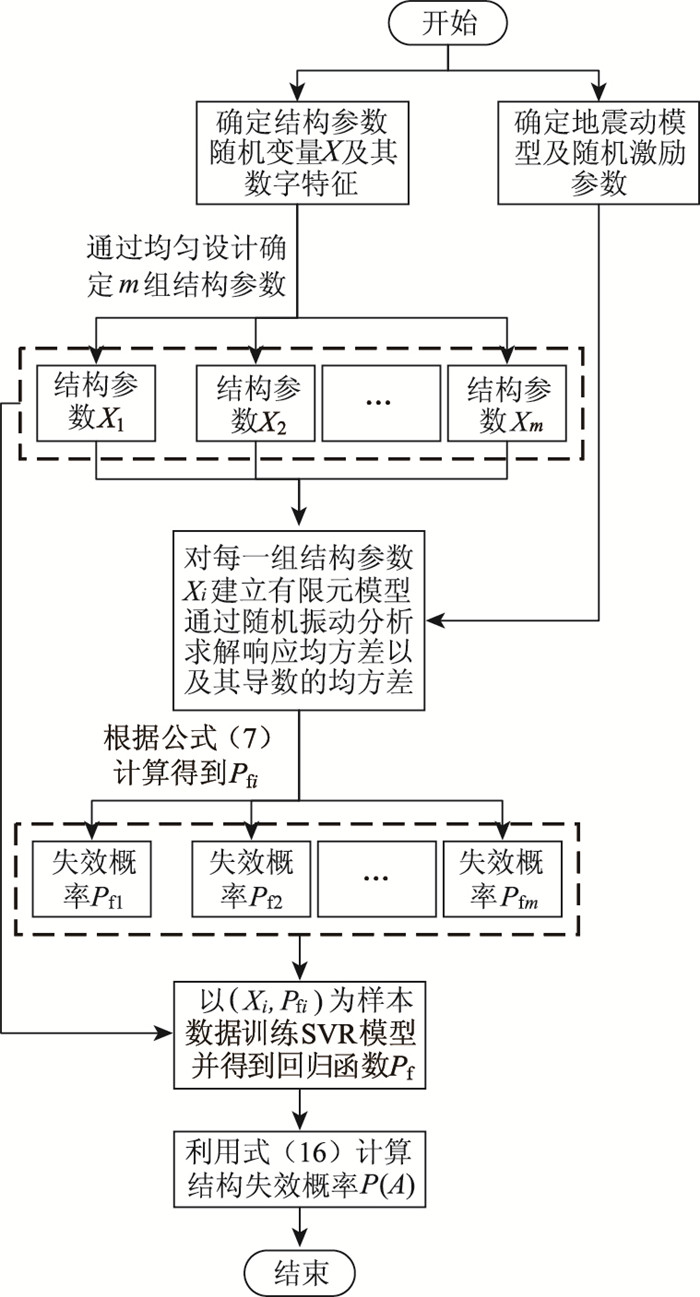
以(Xi,Pfi)作为样本数据训练SVR模型, i=1, 2, …, m,训练过程如图 1所示。选择高斯核函数K(xi, xj)=exp(-γ‖xi-xj‖2)为SVR的核函数,并利用样本数据进行交叉验证寻找SVR模型的最优参数,再训练SVR模型得到回归函数:
|
| 图 1 SVR模型建立流程图 Fig. 1 Flowchart of SVR modeling |
| |
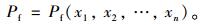
|
(13) |
得到的回归函数将会在后续的计算中被调用,而无需再进行结构有限元分析从而大大节省计算时间。
由于结构有限元分析耗时较长,可以采用均匀设计(Uniform Design, UD)[16]试验方法对结构的随机参数进行抽样选取。均匀设计试验方法从样本分布均匀性的原则出发,均匀设计表可表示为Un(qs),n为试验次数,s为列数,q为每个因素的水平数。在均匀设计中试验次数n与水平数q相等,相对于正交试验的q2次而言降低较多。
2.3 计算结构在双重随机性下的失效概率将结构在双重随机性下失效事件作为复杂事件A,结构参数X的确定作为随机事件B。根据全概率公式的定义可知:

|
(14) |
由于结构参数X是连续型随机变量,所以将全概率公式写成概率密度函数的形式[17]:
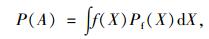
|
(15) |
式中,f(X)为结构参数随机变量的联合概率密度函数;Pf(X)为结构在结构参数为X时的条件概率,即式(13) 中的Pf,积分区间为X的定义域。
由于回归函数Pf(X)一般比较复杂,所以按式(15) 直接积分会难以进行,考虑到式(15) 的形式可以采用蒙特卡罗积分法进行数值积分:
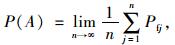
|
(16) |
式中,Pfj由结构参数X按照其分布类型随机取样Xj(x1j, x2j, …, xnj), 再通过式(13) 计算得到。利用matlab软件编写随机抽样程序进行有限次的计算可以快速得到式(16) 的近似解,即为结构失效概率。
基于以上分析,给出结构可靠度计算步骤,如图 2所示。
|
| 图 2 复合随机系统可靠度计算流程 Fig. 2 Flowchart of calculating reliability of complex stochastic system |
| |
3 算例 3.1 工程背景
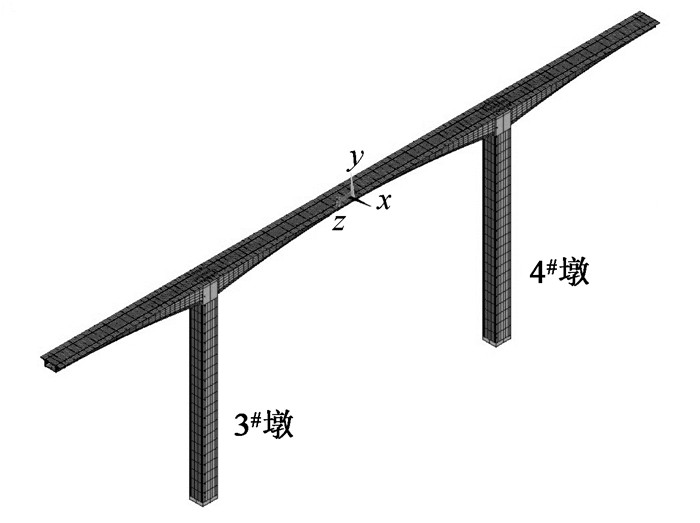
某高墩大跨度预应力连续刚构桥位于Ⅱ类场地,抗震设防烈度Ⅷ度。桥跨布置为(95+180+95) m,墩高分别为105.56 m和116.79 m。主墩为C40混凝土空心矩形截面墩,主梁为C60混凝土箱梁。采用有限元分析软件ANSYS建立了桥梁模型,主梁和主墩均为BEAM188单元,共计159个,如图 3所示。
|
| 图 3 桥梁有限元模型 Fig. 3 Finite element model of bridge |
| |
3.2 地震动模型
桥梁随机地震反应分析中一般采用功率谱密度函数来描述地震动的特征。本研究随机地震动模型采用杜修力模型[18]:
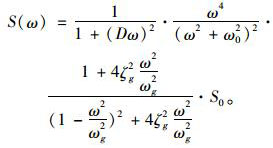
|
(17) |
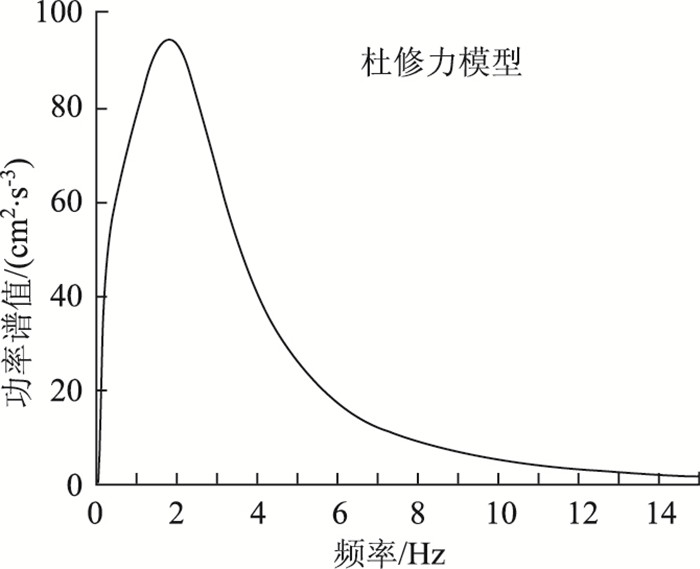
由于地震动强度在地震持时内是一个从弱到强再到弱的过程,并非是一个平稳随机过程。工程上一般采用将平稳过程乘以一个确定性的包络函数来描述非平稳地震动激励。通过调整功率谱模型参数可以将非平稳随机过程等效成平稳随机过程[5]。根据勘察设计资料和文献[18-22]确定功率谱模型参数:高频拐角周期D=0.009 s,低频拐角频率ω0=0.628 rad/s,场地卓越频率ωg=14.52 rad/s,场地土阻尼比ξg=0.726,强度因子S0=60.21 cm2/s3,地震持时T=13.66 s。考虑水平双向地震作用,功率谱密度曲线如图 4所示。
|
| 图 4 功率谱密度函数曲线 Fig. 4 Curve of power spectral density function |
| |
3.3 失效模式及可靠度计算分析
李立峰等对大跨度高墩连续刚构桥进行增量动力分析得出在地震中首先失效的一般是墩底位置[23]。《公路桥梁抗震设计细则》[24]规定A类桥梁在E2地震作用下可发生局部轻微损伤,不需修复或经简单修复可继续使用,故取墩底位置在地震作用下弯矩超限为结构失效标志。
桥梁结构主要随机参数为弹性模量、质量密度,具体统计特征见表 1。试验采用3因素7水平均匀设计,选取均匀设计表U7*(74)中的第2,3,4列作为试验样本,见表 2。
| 随机变量 | 分布类型 | 均值 | 变异系数 |
| 主梁质量密度X1 | 正态 | 26 kN·m-3 | 0.08 |
| 主墩质量密度X2 | 正态 | 25 kN·m-3 | 0.08 |
| 主墩弹性模量X3 | 正态 | 3.25×1010 kN·m-2 | 0.1 |
| 序号 | 1 | 2 | 3 | 4 |
| 1 | 1 | 3 | 5 | 7 |
| 2 | 2 | 6 | 2 | 6 |
| 3 | 3 | 1 | 7 | 5 |
| 4 | 4 | 4 | 4 | 4 |
| 5 | 5 | 7 | 1 | 3 |
| 6 | 6 | 2 | 6 | 2 |
| 7 | 7 | 5 | 3 | 1 |
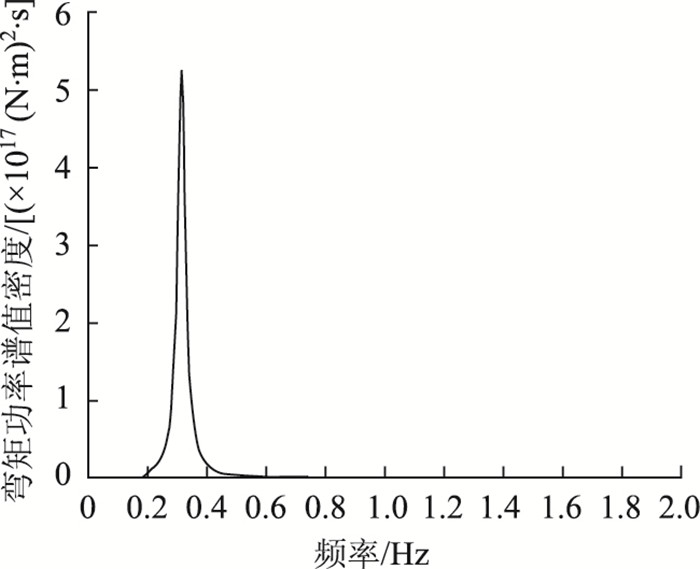
再对3种结构参数分别选定7个水平(μ-3σ,μ-2σ,…,μ+3σ)并与表 2中的7个水平(1,2,…,7) 一一对应,得到表 3中的试验点。根据每组试验点修改ansys有限元模型中的结构参数数据,进行功率谱密度(PSD)分析,得出响应功率谱密度曲线,见图 5。
| 试验号 | 随机变量 | 失效概率 | ||||
| X1 | X2 | X3 | 3#墩底 | 4#墩底 | ||
| 1 | μ1-σ1 | μ2+σ2 | μ3+3σ3 | 8.533×10-4 | 4.318×10-3 | |
| 2 | μ1+2σ1 | μ2-2σ2 | μ3+2σ3 | 5.076×10-5 | 1.060×10-4 | |
| 3 | μ1-3σ1 | μ2+3σ2 | μ3+σ3 | 6.963×10-5 | 4.158×10-4 | |
| 4 | μ1 | μ2 | μ3 | 1.257×10-6 | 7.877×10-7 | |
| 5 | μ1+3σ1 | μ2-3σ2 | μ3-σ3 | 2.048×10-8 | 4.203×10-10 | |
| 6 | μ1-2σ1 | μ2+2σ2 | μ3-2σ3 | 1.223×10-8 | 7.615×10-10 | |
| 7 | μ1+σ1 | μ2-σ2 | μ3-3σ3 | 4.701×10-11 | 1.170×10-12 | |
|
| 图 5 3#墩墩底弯矩功率谱密度曲线 Fig. 5 Curve of PSD of moment at 3rd pier bottom |
| |
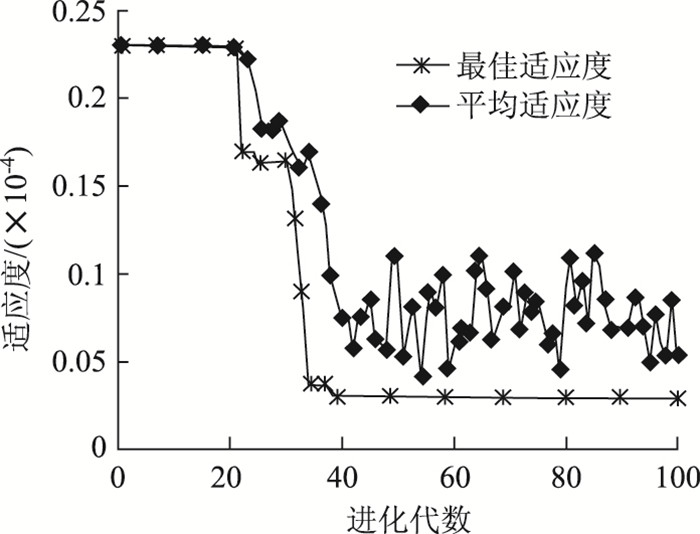
根据首超准则计算出墩底位置的失效概率,见表 3。选择高斯核函数作为SVR核函数,利用得出的样本数据训练SVR,并选择遗传算法(GA)寻找最优参数C和γ,见图 6。最后根据式(16) 在matlab软件中编写随机抽样程序计算出结构失效概率,见表 4。
|
| 图 6 基于GA的SVR参数寻优 Fig. 6 SVR parameter optimization based on GA |
| |
| 计算方法 | 3#墩底 | 4#墩底 | 有限元计算次数 | |||
| 失效概率 | 可靠指标 | 失效概率 | 可靠指标 | |||
| 不考虑结构参数随机性 | 1.257×10-6 | 4.71 | 7.877×10-7 | 4.80 | 1 | |
| UD-SVR | 3.239×10-5 | 3.99 | 1.067×10-4 | 3.70 | 7 | |
同时给出不考虑结构参数随机性计算得出的桥梁抗震可靠指标,通过对比可知在本例中如果不考虑结构参数随机性可能会高估结构的安全性能,再次说明了桥梁抗震设计中应重视地震动激励与结构参数双重随机性对结构的影响。
4 结论通过支持向量回归(SVR)与首超准则分析了复合随机结构在地震作用下的动力可靠度,主要得出以下结论:
(1) 采用UD-SVR方法拟合了关于结构参数与失效概率的响应面函数,并基于此进行可靠度分析,提高了桥梁结构抗震可靠度的计算效率。
(2) 采用均匀设计试验方法,该方法仅考虑试验点在试验范围内的均匀散布,有效减少了结构有限元分析次数。
(3) 本文方法原理清晰,计算过程中可运用现有商业有限元分析软件,适用于复杂桥梁结构的抗震可靠度分析。
| [1] | KIUREGHIAN A D, FUJIMURA K. Nonlinear Stochastic Dynamic Analysis for Performancebased Earthquake Engineering[J]. |
| [2] | 欧进萍, 侯钢领, 吴斌. 概率Pushover分析方法及其在结构体系抗震可靠度评估中的应用[J]. 建筑结构学报, 2001, 22(6): 81-86 OU Jin-ping, HOU Gang-ling, WU Bin. Random Pushover Analysis Method and Its Application in Earthquake-resistant Reliability Evaluation of Structural Systems[J]. Journal of Building Structures, 2001, 22(6): 81-86 |
| [3] | 李杰, 李建华. 多点激励下结构随机地震反应分析的反应谱方法[J]. 地震工程与工程振动, 2004, 24(3): 21-29 LI Jie, LI Jian-hua. A Response Spectrum Method for Random Vibration Analysis of Structures under Multi-support Excitations[J]. Earthquake Engineering and Engineering Vibration, 2004, 24(3): 21-29 |
| [4] | 韩兴, 李鑫, 向宝山, 等. 基于IDA方法的高速铁路连续梁桥易损性分析[J]. 公路交通科技, 2016, 33(2): 54-59 HAN Xing, LI Xin, XIANG Bao-shan, et al. Analysis of Seismic Fragility of High Speed Railway Continuous Beam Bridge Based on IDA Method[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2): 54-59 |
| [5] | 武芳文. 大跨度斜拉桥随机地震响应分析及其动力可靠度研究[D]. 成都: 西南交通大学, 2008. WU Fang-wen. Study of Long Span Cable-stayed Bridges Stochastic Seismic Response and Dynamic Reliability[D].Chengdu:Southwest Jiaotong University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10613-2008178941.htm |
| [6] | 李志强, 李金贝, 孔亚平. 基于地震响应分析的公路挡土结构物抗震动力可靠性[J]. 公路交通科技, 2011, 28(12): 32-38 LI Zhi-qiang, LI Jin-bei, KONG Ya-ping. Aseismic Dynamic Reliability of Highway Soil Retaining Structure Based on Seismic Response Analysis[J]. Journal of Highway and Transportation Research and Development, 2011, 28(12): 32-38 |
| [7] | 吕大刚, 宋鹏彦, 于晓辉, 等. 结构动力抗震可靠度理论的研究进展[J]. 西南交通大学学报, 2015, 50(6): 1025-1038 LÜ Da-gang, SONG Peng-yan, YU Xiao-hui, et al. State-of-the-art of Dynamic Seismic Reliability Theories of Structures[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 1025-1038 |
| [8] | 陈兵, 赵雷, 陈思孝. 高墩大跨连续刚构铁路桥抗震可靠度分析[J]. 铁道学报, 2008, 30(2): 113-117 CHEN Bing, ZHAO Lei, CHEN Si-xiao. Anti-seismic Reliability Analysis of the High-pier Long-span Continuous Rigid Frame Railway Bridge[J]. Journal of the China Railway Society, 2008, 30(2): 113-117 |
| [9] | 陈建兵, 李杰. 随机结构复合随机振动分析的概率密度演化方法[J]. 工程力学, 2004, 21(3): 90-95 CHEN Jian-bing, LI Jie. The Probability Density Evolution Method for Compound Random Vibration Analysis of Stochastic Structures[J]. Engineering Mechanics, 2004, 21(3): 90-95 |
| [10] | 陈颖, 宁佐贵. 基于神经网络响应面法的随机结构动力可靠度分析[J]. 振动与冲击, 2007, 26(1): 65-68, 161 CHEN Ying, NING Zuo-gui. Dynamic Reliability Analysis of a Stochastic Structure with Neural Network Response Surface Method[J]. Journal of Vibration and Shock, 2007, 26(1): 65-68, 161 |
| [11] | 贾布裕, 余晓琳, 颜全胜, 等. 基于Kriging改进响应面法的桥梁地震动力可靠度研究[J]. 振动与冲击, 2013, 32(16): 82-87, 105 JIA Bu-yu, YU Xiao-lin, YAN Quan-sheng, et al. Bridge Seismic Reliability Analysis Based on Improved Kriging Response Surface Method[J]. Journal of Vibration and Shock, 2013, 32(16): 82-87, 105 |
| [12] | RICE S O. Mathematical Analysis of Random Noise[J]. |
| [13] | VAPNIK V N. The Nature of Statistical Learning Theory[M]. New York: Springer, 1995. |
| [14] | 刘扬, 鲁乃唯, 殷新锋. 基于更新支持向量的大跨度斜拉桥体系可靠度分析[J]. 计算力学学报, 2015, 32(2): 154-159 LIU Yang, LU Nai-wei, YIN Xin-feng. System Reliability Assessment of Long-span Cable-stayed Bridges Using an Updating Support Vector Algorithm[J]. Chinese Journal of Computational Mechanics, 2015, 32(2): 154-159 |
| [15] | GUO Zhi-wei, BAI Guang-chen. Application of Least Squares Support Vector Machine for Regression to Reliability Analysis[J]. Chinese Journal of Aeronautics, 2009, 22(2): 160-166 |
| [16] | FANG Kai-tai. The Uniform Design:Application of Number-Theoretic Methods in Experimental Design[J]. Acta Mathematicae Applicatae Sinica, 1980, 3(4): 363-372 |
| [17] | 徐辉, 邬国根. 基于条件期望的全概率公式及其应用[J]. 东华理工学院学报, 2004, 27(2): 193-195 XU Hui, WU Guo-gen. Full Probability Formula Based on the Conditional Expectation and Its Applications[J]. Journal of East China University of Technology, 2004, 27(2): 193-195 |
| [18] | 杜修力, 胡晓, 陈厚群. 强震地运动随机过程模拟[J]. 地震学报, 1995(1): 103-109 DU Xiu-li, HU Xiao, CHEN Hou-qun. Simulation of Random Process of Strong Ground Motion[J]. Acta Seismologica Sinica, 1995(1): 103-109 |
| [19] | 欧进萍, 牛荻涛, 杜修力. 设计用随机地震动的模型及其参数确定[J]. 地震工程与工程振动, 1991, 11(3): 45-54 OU Jin-ping, NIU Di-tao, DU Xiu-li. Random Earthquake Ground Motion Model and Its Parameter Determination Used in Aseismic Design[J]. Earthquake Engineering and Engineering Vibration, 1991, 11(3): 45-54 |
| [20] | 牛荻涛, 欧进萍. 设计用随机地震动模型与参数的改进[J]. 西安建筑科技大学学报, 1994(1): 30-35 NIU Di-tao, OU Jin-ping. Random Earthquake Ground Motion Model and Its Parameter Modification Used in Aseismic Design[J]. Journal of Xi'an University of Architecture & Technology, 1994(1): 30-35 |
| [21] | 周佩佩, 巢斯. 对应新抗震规范反应谱的功率谱模型参数研究[J]. 建筑结构, 2013, 增2: 430-435 ZHOU Pei-pei, CHAO Si. Parameters Research on Seismic Power Spectrum Model Based on the New Seismic Design Code for Buildings[J]. Building Structure, 2013, 增2(S2): 430-435 |
| [22] | 李英民, 刘立平, 赖明. 工程地震动随机功率谱模型的分析与改进[J]. 工程力学, 2008, 25(3): 43-48, 57 LI Ying-min, LIU Li-ping, LAI Ming. Analysis and Improvement of Power Random Spectra of Strong Ground Motions for Engineering Purpose[J]. Engineering Mechanics, 2008, 25(3): 43-48, 57 |
| [23] | 李立峰, 黄佳梅, 吴文朋, 等. 基于IDA的高墩大跨桥梁抗震性能评估[J]. 地震工程与工程振动, 2012, 32(1): 68-77 LI Li-feng, HUANG Jia-mei, WU Wen-peng, et al. Research on the Seismic Performance of Bridge with High Piers and Long Spans Using Incremental Dynamic Analysis[J]. Earthquake Engineering and Engineering Vibration, 2012, 32(1): 68-77 |
| [24] | JTG/T B02-01-2008, 公路桥梁抗震设计细则[S]. JTG/T B02-01-2008, Guidelines for Seismic Design of Highway Bridges[S]. |
 2017, Vol. 34
2017, Vol. 34
