扩展功能
文章信息
- 高燕梅, 刘东, 周志祥, 许逸雪
- GAO Yan-mei, LIU Dong, ZHOU Zhi-xiang, XU Yi-xue
- 考虑施工阶段的装配式钢-混凝土组合梁非线性全过程分析方法
- A Nonlinear Whole Process Analysis Method of Prefabricated Steel-concrete Composite Beam Considering Construction Stages
- 公路交通科技, 2017, 34(9): 52-59
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(9): 52-59
- 10.3969/j.issn.1002-0268.2017.09.008
-
文章历史
- 收稿日期: 2017-03-29
2. 重庆交通大学 山区桥梁与隧道工程国家重点实验室培育基地, 重庆 400074
2. State Key Laboratory Cultivation Base of Mountain Bridge and Tunnel Engineering, Chongqing Jiaotong University, Chongqing 400074, China
采用预制桥道板的钢-混凝土组合梁是现代组合梁的一个发展趋势,它可以缩短施工工期,降低造价,解决现浇混凝土板收缩徐变大的问题[1-3],各国研究者针对此类组合梁负弯矩作用下的工作性能进行了一系列试验和理论研究,并应用于国内外一些桥梁[4-7],例如我国港珠澳大桥浅水区的非通航孔组合连续梁桥。
研究者们为了掌握钢-混凝土组合梁从加载到破坏全过程的受力性能,根据其构造特点,提出了一些全过程模拟分析方法[8-13]。赵洁、聂建国[8]在考虑材料非线性和栓钉滑移的基础上,建立二维平面模型,得到了构件从弹性到破坏全过程的力学性能。何光辉、杨骁[9]针对连续钢-混凝土组合梁,提出可分别应用Reddy、Timoshenko和Euler-Bernoulli组合梁有限单元进行准静力分析,并考察了剪切效应对组合梁构件的挠度、黏结层滑移和截面应力的影响。林建平[10]通过引入无厚度单元模拟钢与混凝土界面的非连续变形,提出了基于强化有限元的考虑界面滑移的组合梁分析模型建立方法。胡少伟[11]基于VB语言,采用共轭梁法、弯矩曲率法编制了组合梁从加载到破坏全过程的非线性分析软件,并将计算结果与已有的试验结果对比,验证了方法的正确性。
以上研究者们在考虑材料非线性、剪力键滑移影响以及几何非线性影响的基础上,提出了适用于不同钢-混凝土组合梁或者组合框架结构的全过程受力分析方法。但是以上方法均未考虑施工阶段对组合梁受力性能的影响,特别是全装配式钢-混凝土组合梁[14],以上方法不再适用。
装配式钢-混凝土组合梁希望不通过现浇混凝土实现预制混凝土桥道板与钢桁上弦的剪力联结,提出在预制混凝土桥道板中预埋带栓钉的剪力钢板,待预制桥道板安装就位,预应力钢束张拉完成,再将桥道板肋的预埋剪力传递钢板与钢桁顶板间的纵缝施焊联结形成组合梁。对于装配式钢-混凝土组合梁,不考虑施工阶段的非线性全过程分析将会导致桥道板无法单独获得预压应力,也无法模拟带应力的钢桁与桥道板联结为整体的工况。这样会使得在使用阶段承受负弯矩时,混凝土桥道板提前开裂而退出工作,从而组合梁提早进入塑性工作阶段直至破坏。
为了研究装配式钢桁-混凝土组合梁在负弯矩作用下,从施工到成桥到破坏的全过程力学行为,在考虑材料非线性的基础上,对其精细化有限元分析方法进行研究,并结合该组合梁负弯矩区段力学行为试验,验证计算结果的正确性。
1 装配式钢桁-混凝土组合梁概念为了减少混凝土现浇工作,减少预制混凝土桥道板与后浇剪力键预留孔、现浇混凝土接缝因龄期差异出现的开裂,简化桥道板构造,加快施工进度同时提高施工质量,本研究提出了一种装配式钢桁-混凝土(Prefabricated steel truss-concrete(PSTC))组合梁如图 1所示,其关键构造有三:(1) PCSS(Prefabricated Composite Shear Studs)剪力联结构造:即在预制混凝土桥道板中预埋水平栓钉剪力联结键[15],再与钢结构通过后焊联结成为装配式钢-混凝土组合结构。这样可以避免在预制桥道板上预留剪力键后浇孔,减少混凝土现浇工作,避免了剪力键预留孔无法获得预应力储备和角隅应力集中的问题。PCSS剪力键是在已有研究的基础上提出的新型剪力键构造形式,已进行剪力键推出试验[16]。(2) 采用预制混凝土桥道板如图 2所示,先预制安装混凝土桥道板,再张拉预应力钢束,最后将PCSS剪力键竖钢板与钢桁顶面之间的纵缝施焊形成组合梁,预压应力全部由桥道板承受,有效地提高组合梁桥道板的抗裂性能。(3) 板间直缝联结:即板间无需设置企口或扣环现浇混凝土接缝构造,而代之以涂抹粘结胶联结,减少了预制混凝土桥道板与现浇混凝土接缝因龄期差异出现的开裂,简化了桥道板构造。

|
| 图 1 装配式钢桁-混凝土组合梁(PSTC组合梁)的概念设计 Fig. 1 Concept design of prefabricated steel truss-concrete composite beam |
| |
|
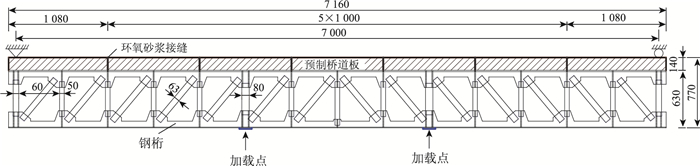
| 图 2 l=7 000 mm的PSTC组合梁(单位: mm) Fig. 2 PSTC beam when l=7 000 mm (unit: mm) |
| |
PSTC组合梁的施工工序是:(1) 预制混凝土桥道板(预埋PCSS剪力键),同时工厂制作钢桁;(2) 在钢桁上安装预制混凝土桥道板,板间接缝处涂抹粘结胶,施行板间接缝联结;(3) 对桥道板施加预应力,预应力孔道灌浆;(4) 将剪力键钢板与钢桁上弦杆的翼缘顶面焊接联结,使钢桁梁与混凝土桥道板形成组合梁,完成施工。
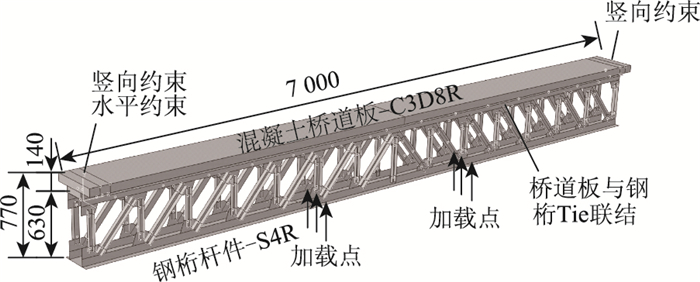
2 考虑施工阶段的非线性有限元建模方法为了探索一种组合梁考虑施工阶段受力的非线性全过程分析方法,掌握装配式钢-混凝土(PSTC)组合梁承受负弯矩时的力学行为,以试验梁为依据,应用有限元分析软件ABAQUS,建立l=7 000 mm的简支PSTC组合梁有限元模型,如图 2所示,并采用在下端两点顶升钢桁梁的方式来模拟负弯矩区段加载。
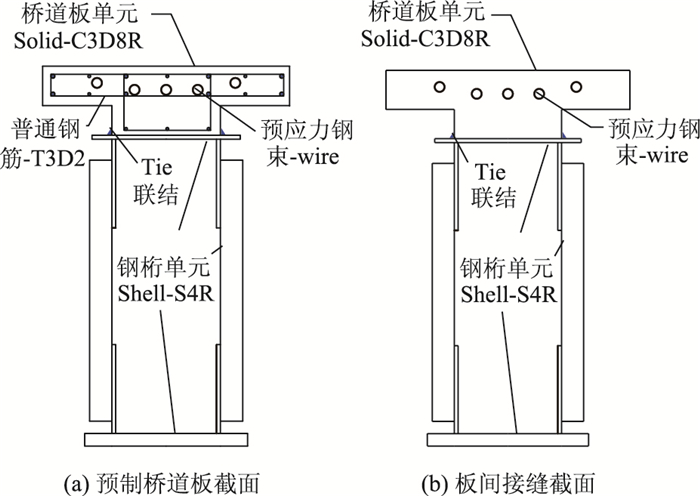
2.1 预制桥道板与接缝模拟PSTC组合梁的单元选取和接触关系如图 3所示,混凝土桥道板采用实体单元C3D8R,钢桁杆件采用壳单元S4R,预应力钢束和普通钢筋采用桁架单元T3D2;预制混凝土桥道板与预应力钢束、普通钢筋之间采用嵌入关系,板间接缝处无普通钢筋。
|
| 图 3 PSTC组合梁有限元建模 Fig. 3 Finite element modeling of PSTC beam |
| |
2.2 施工工序模拟
(1) 钢桁梁加载
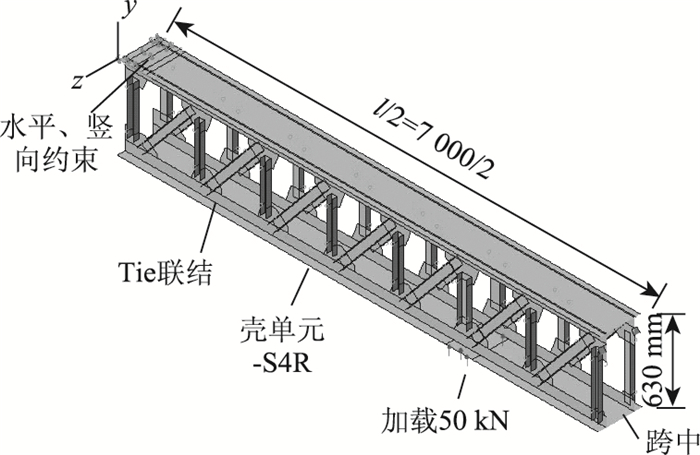
当PSTC组合梁用于采用悬臂拼装施工的连续刚构桥时,钢桁梁在悬拼过程中将产生应力,随后才根据受力需要适时安装预制桥道板,钢桁梁承受桥道板自重。因此在计算分析时,为了模拟PSTC组合梁按照以上方法施工时的力学行为,首先对纯钢桁施加了2个50 kN的外荷载如图 4、图 5所示,并将桥道板重量作为均布荷载作用于钢桁上弦。桥道板本身重度设置为0。计算模型中钢桁采用壳单元S4R模拟,桁架杆件之间采用Tie联结。

|
| 图 4 钢桁试验梁加载 Fig. 4 Loading on steel truss test beam |
| |
|
| 图 5 l/2的钢桁梁有限元模型 Fig. 5 Finite element model of l/2 steel truss beam |
| |
(2) 桥道板施加预应力阶段
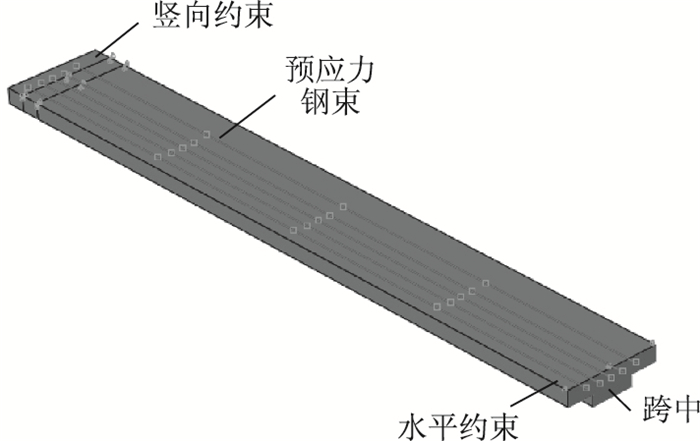
为了真实模拟桥道板施加预应力阶段,桥道板与钢桁之间在该阶段计算时不设置任何联结,并且为了使桥道板两端变形均匀,在板端施加竖向约束,跨中施加水平约束如图 6所示。
|
| 图 6 l/2的预应力混凝土桥道板有限元模型 Fig. 6 Finite Element Model of the l/2 prestressed concrete deck |
| |
采用降温法来实现桥道板内施加预应力:对模型中的钢束实施降温,使钢束的最终变形量等于钢束张拉时的伸长量,使得钢束周围的混凝土获得同等预压应力:
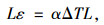
|
(1) |
式中预应力筋的线膨胀系数α=1.2×105。
(3) 桥道板与钢桁之间刚性联结形成组合梁
另建立一个组合梁计算模型如图 7所示,该模型的边界条件与上述钢桁及桥道板模型相同,但钢桁和混凝土桥道板之间采用Tie联结以模拟PCSS剪力键按完全抗剪联结设计的情况,并通过施加初始应力的方法将已获得预压力的桥道板的计算结果文件导入该组合梁模型。
|
| 图 7 PSTC组合梁有限元模型(单位: mm) Fig. 7 Finite element model of PSTC beam (unit: mm) |
| |
2.3 本构关系
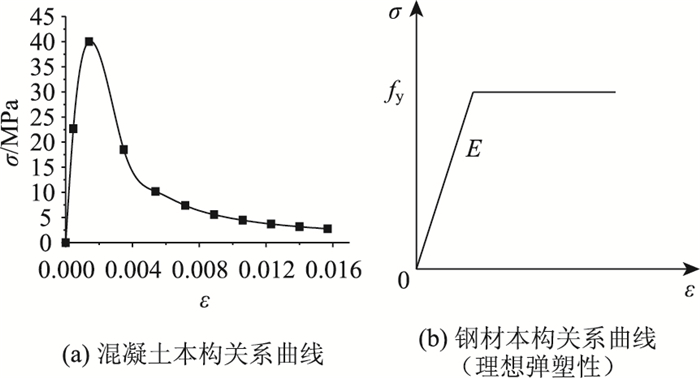
混凝土采用ABAQUS中的塑性损伤(Concrete Damage Plasticity)模型,这是一个基于塑性的连续介质损伤模型[17]。该模型假设的两种主要破坏方式为混凝土受拉开裂和受压压溃,可用于单向加载、循环加载及动态加载等情况, 具有较好的收敛性。混凝土的等效受压应力-应变关系曲线采用Hongnestad公式,如图 8(a)所示,并假设混凝土在达到峰值应力的1/3前均为线弹性材料,弹性模量Ec为定值,按式(2) 计算:
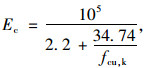
|
(2) |
|
| 图 8 材料本构关系曲线 Fig. 8 Constitutive relationship curves of materials |
| |
式中fcu, k为混凝土标准立方体抗压强度。
进行立方体试块的抗压试验,数值分析中采用的棱柱体抗压强度换算关系式[11]为:
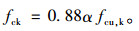
|
(3) |
混凝土轴心抗拉强度标准值[11]为:
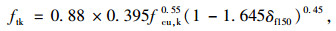
|
(4) |
式中δf150列于《钢筋混凝土及预应力混凝土桥涵设计规范》[18]附录A.0.1-1中。混凝土的泊松比通常为0.16~0.23,模型中均取为0.2。
本次试验梁的Q345钢和普通钢筋均采用理想弹塑性模型,形式简单,能近似地描述钢材受力性能,如图 8(b)所示。
2.4 组合梁受载模拟由于分析中包括了混凝土开裂、钢板和钢筋的塑性变形,需要使用非线性迭代技术求解。采用了ABAQUS中Newton-Raphson平衡迭代法。对于一个小的荷载增量ΔP,ABAQUS计算出迭代的残差力并与容许值进行比较,默认的容许值设置为在整个时间段上作用于结构上平均力的0.05%,若残差力小于容许值,则认为达到平衡状态。
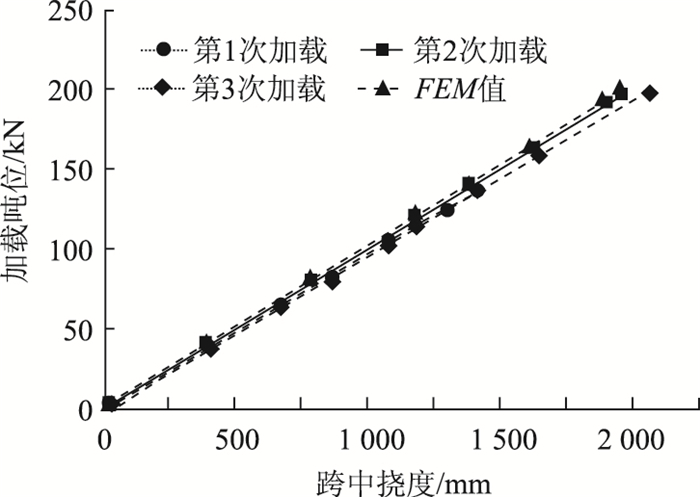
3 计算结果与试验结果对比分析 3.1 钢桁梁加载阶段为了验证钢桁模型计算正确与否,分别将钢桁试验梁和计算模型均加载至200 kN,从图 9和表 1可以看出,计算值与钢桁试验梁3次加载的跨中挠度值相比,最小差值为0.2%,最大差值4%,吻合程度良好,可以进行下一步计算。且跨中挠度值与加载吨位呈线性分布,表明钢桁处于弹性状态,受力状态良好。
|
| 图 9 钢桁跨中挠度计算值与实测值对比 Fig. 9 Comparison of steel truss mid-span deflection between calculated value and measured value |
| |
| 加载 | 计算值/mm | 实测值/mm | 实测值/计算值 |
| 第1次 | 12.60 | 13.03 | 1.03 |
| 第2次 | 12.14 | 0.96 | |
| 第3次 | 12.58 | 0.998 |
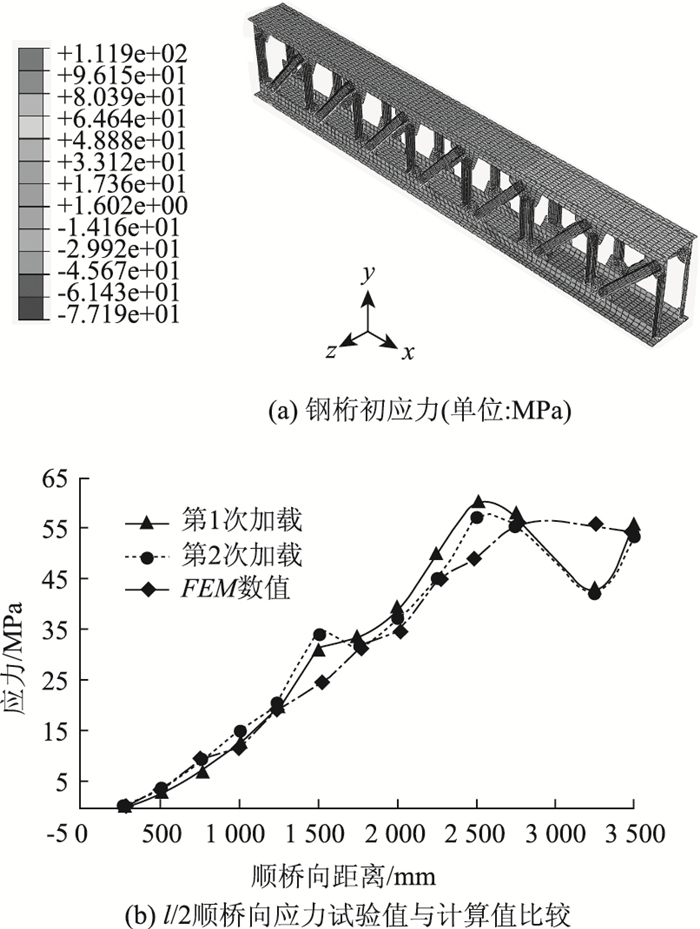
对纯钢桁施加两个向上50 kN的外荷载,并将桥道板重量作为均布荷载作用于上弦。钢桁梁的初应力状态如图 10(a)所示。图 10(b)可以看出,从支点到跨中,大部分截面计算值与试验加载应力值比较吻合,仅靠近l/4截面、加载点截面和靠近l/2截面应力差值较大,最大差值23%,主要原因是:① 试验梁的应变片受外界因素影响较大,部分截面测量误差较大;② 加载点处,计算时是施加的面荷载,而试验时出现的应力集中现象比计算中严重,所以应力在此处出现了一个峰值。
|
| 图 10 钢桁梁施加初应力状态 Fig. 10 Initial stress applied on PSTC beam |
| |
3.2 桥道板施加预应力阶段
试验梁的混凝土桥道板有效预压应力为10.6 MPa,如图 11所示,降温法可以使计算模型中的桥道板获得同样大小的预压应力。

|
| 图 11 桥道板获得预压应力(单位:MPa) Fig. 11 Prestress obtained by precast deck (unit: MPa) |
| |
3.3 桥道板与钢桁之间刚性联结形成组合梁
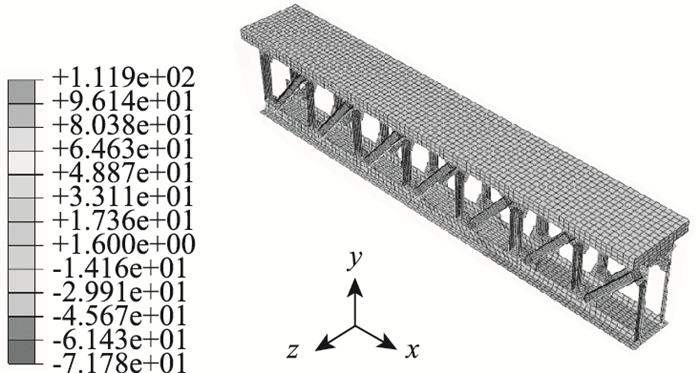
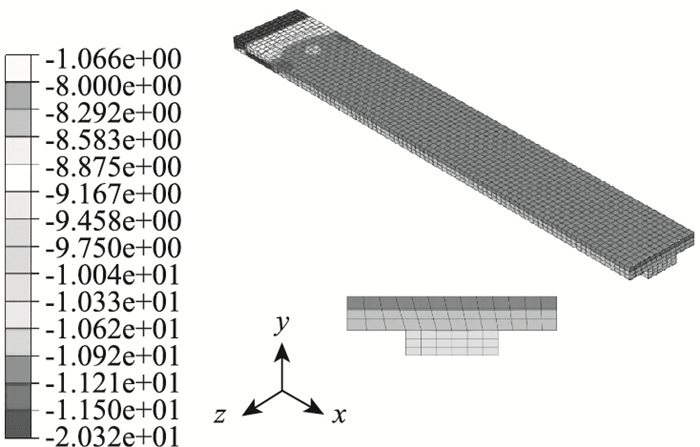
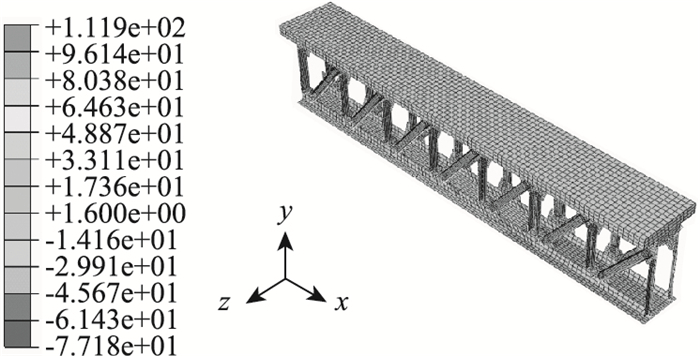
将前述3.2节桥道板的计算结果文件导入组合梁模型。这样在组合梁的初始状态时,如图 12所示;桥道板内初应力亦如前述§3.2节获得的预压应力,如图 13所示;钢桁的受力状态如前述3.1节纯钢桁的受力状态,如图 14所示。
|
| 图 12 组合梁的初应力状态(单位:MPa) Fig. 12 Initial stress of PSTC beam (unit: MPa) |
| |
|
| 图 13 组合梁中桥道板的初应力状态(单位:MPa) Fig. 13 Initial stress of precast deck in PSTC beam (unit: MPa) |
| |
|
| 图 14 组合梁中钢桁梁的初应力状态(单位:MPa) Fig. 14 Initial stress of steel truss in PSTC beam (unit: MPa) |
| |
3.4 组合梁加载阶段
(1) 荷载-挠度结果分析
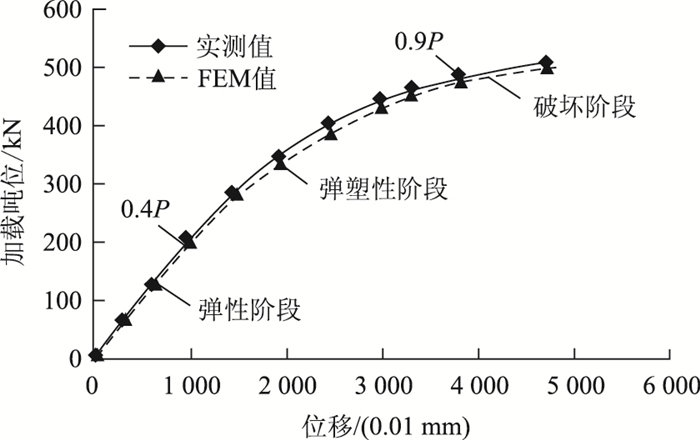
从图 15、图 16可以看出,跨中挠度的有限元计算值与实测值趋势吻合很好,例如试验梁加载至480 kN时,跨中最大挠度38.03 mm,有限元计算值39.67 mm,差值4.1%。
|
| 图 15 PSTC跨中挠度有限元计算值与实测值对比 Fig. 15 Comparison of mid-span deflection between FE calculated value and measured value |
| |
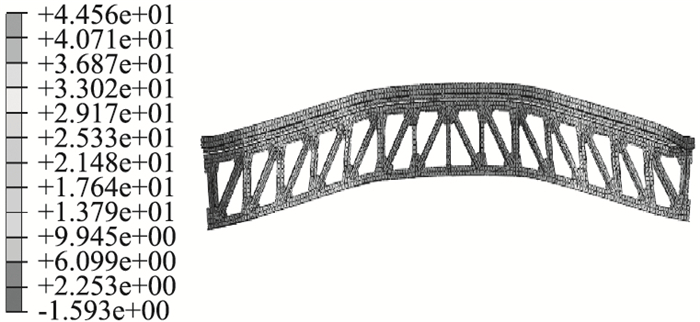
|
| 图 16 组合梁位移图(单位:mm) Fig. 16 Deflection of PSTC beam (unit: mm) |
| |
从图 15的试验梁实测曲线和FEM计算曲线对比可以看出,当P<0.4 Pu时,结构处于弹性受力阶段,两条曲线基本重合,构件的荷载-挠度呈直线;0.4Pu<P<0.9Pu时,组合梁处于弹塑性工作阶段,荷载-位移曲线出现折点,不再呈直线走向;当超过0.9Pu后,组合梁进入破坏阶段,变形迅速增加,临近破坏时荷载-位移曲线基本呈水平趋势,说明钢桁达到屈服强度,组合梁破坏。
(2) 裂缝发展分析
计算时PSTC组合梁的混凝土板裂缝最早出现在加载点附近的5#板,加载吨位198 kN,而试验梁加载至190 kN出现裂缝,加载吨位及初始裂缝位置吻合较好如图 17所示。随着荷载的增加,混凝土板上的裂缝发展趋势和试验结果亦吻合较好如图 18所示,有限元模型能较真实模拟结构全过程的开裂和桥道板的破坏行为。
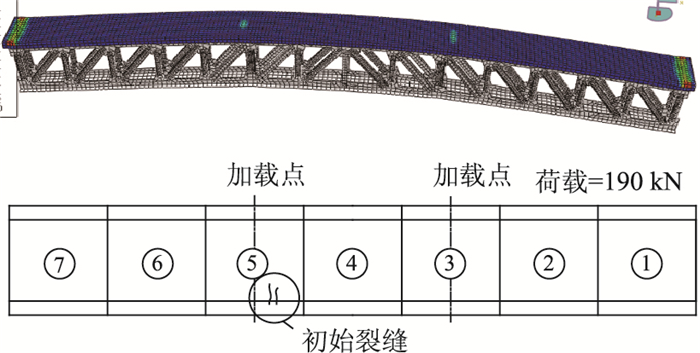
|
| 图 17 桥道板初始裂缝 Fig. 17 Initial crack of precast deck |
| |
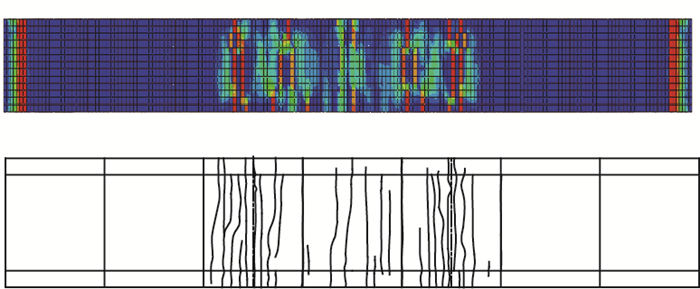
|
| 图 18 桥道板裂缝对比 Fig. 18 Comparison of cracks |
| |
(3) 破坏状态
计算模型中当加载到50.2 t时,钢桁竖杆压应力也已超过345 MPa,认为钢桁已经屈服。此时荷载-挠度曲线基本呈水平趋势,说明钢桁达到屈服强度,组合梁破坏(图 19)。
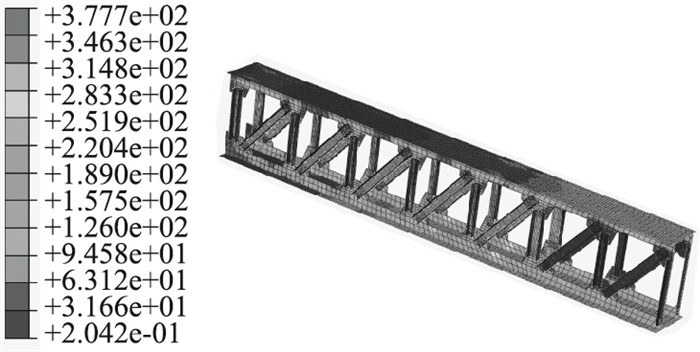
|
| 图 19 PSTC试验梁破坏时钢桁应力(单位:MPa) Fig. 19 Stress of steel truss when PSTC test beam damaged (unit: MPa) |
| |
4 结论
(1) 相比常规组合梁,装配式钢-混凝土组合梁的3个关键施工环节是:① 在预制混凝土桥道板肋中预埋带水平栓钉的剪力传递钢板。② 安装预制混凝土桥道板(接缝处涂抹粘结胶)。③ 最后实施桥道板肋的预埋剪力传递钢板与钢桁顶板之间的后焊联结,形成组合梁。由此基本克服了局部现浇混凝土施工质量及后期收缩徐变的不定性,减少了后期开裂病害隐患;预应力全部由预制桥道板承担,提高了桥道板抗裂性能,并简化施工,缩短工期。
(2) 提出了一种适用于装配式钢-混凝土组合梁的考虑施工阶段的非线性全过程分析方法:建立精细化有限元模型,预制桥道板和板间接缝采用在混凝土实体单元中是否嵌入普通钢筋单元分别模拟;采用使预应力钢束降温的方法实现在桥道板内施加预压应力;采用导入初应力的方法,实现了将先期获得预压应力的桥道板与钢桁结整为组合梁共同受力。
(3) 利用该方法模拟分析了组合梁在负弯矩作用下,从施工到成桥到破坏的全过程力学行为,并与组合梁负弯矩区段试验结果对比:该模拟方法能较真实模拟结构全过程的弹性受力阶段、开裂阶段和桥道板的破坏行为,挠度计算值与实测值相差4.1%,吻合较好,可供同类桥梁参考。
| [1] | CHAUDHARY S, PENDHARKAR U, NAGPAL A K. Control of Creep and Shrinkage Effects in Steel Concrete Composite Bridges with Precast Decks[J]. Journal of Bridge Engineering, 2009, 14(5): 336-345 |
| [2] | 李法雄, 王晓夫, 黄厚卿, 等. 钢-混凝土组合梁斜拉桥收缩徐变影响[J]. 公路交通科技, 2013, 30(10): 54-60 LI Fa-xiong, WANG Xiao-fu, HUANG Hou-qing, et al. Impact of Shrinkage and Creep on Steel-concrete Composite Cable-stayed Bridge[J]. Journal of Highway and Transportation Research and Development, 2013, 30(10): 54-60 |
| [3] | 吕朝锋, 杨庆卫, 陈伟球. 收缩徐变对钢-混凝土组合梁弯曲变形的影响分析[J]. 建筑结构学报, 2010, 31(7): 32-39 LÜ Chao-feng, YANG Qing-wei, CHEN Wei-qiu. Effects of Shrinkage and Creep Strains on Bending Behavior of Steel-concrete Composite Beams[J]. Journal of Building Structures, 2010, 31(7): 32-39 |
| [4] | HÄLLMARK R, WHITE H, COLLIN P. Prefabricated Bridge Construction across Europe and America[J]. Practice Periodical on Structural Design & Construction, 2012, 17(3): 82-92 |
| [5] | SHIM C S, CHUNG C H, KIM I K, et al. Development and Application of Precast Slabs for Composite Bridges[J]. Structural Engineering International, 2010, 20(2): 126-133 |
| [6] | 罗扣, 王东晖, 张强. 港珠澳大桥浅水区非通航孔桥组合梁设计[J]. 桥梁建设, 2013, 43(3): 99-102 LUO Kou, WANG Dong-hui, ZHANG Qiang. Design of Composite Girders for Non-navigable Span Bridge of Hong Kong-Zhuhai-Macau Bridge in Shallow Water Area[J]. Bridge Construction, 2013, 43(3): 99-102 |
| [7] | PAPASTERGIOU D T, LEBET J P. New Steel-concrete Connection for Composite Bridges[J]. Stahlbau, 2011, 80(12): 894-903 |
| [8] | 赵洁, 聂建国. 钢板-混凝土组合梁的非线性有限元分析[J]. 工程力学, 2009, 26(4): 105-112 ZHAO Jie, NIE Jian-guo. Nonlinear Finitite Element Analysis of Steel Plate-concrete Composite Beams[J]. Engineering Mechanics, 2009, 26(4): 105-112 |
| [9] | 何光辉, 杨骁. Reddy高阶组合梁的非线性有限元分析[J]. 工程力学, 2015, 32(8): 87-95 HE Guang-hui, YANG Xiao. Nonlinear Analysis of Composite Beams Using Reddy's Higher Order Beam Theory[J]. Engineering Mechanics, 2015, 32(8): 87-95 |
| [10] | 林建平, 汪劲丰, 徐荣桥, 等. 有限元的考虑界面滑移的组合梁数值模拟[J]. 工程力学, 2015, 32(8): 139-140 LIN Jian-ping, WANG Jin-feng, XU Rong-qiao, et al. Enhanced Finite Element Analysis of Composite Beams with Interlayer Slips[J]. Engineering Mechanics, 2015, 32(8): 139-140 |
| [11] | 胡少伟, 叶祥飞. 预应力连续组合梁负弯矩区受弯全过程分析[J]. 水电能源科学, 2013(12): 122-125 HU Shao-wei, YE Xiang-fei. Whole Process Analysis of Flexural Behavior of Negative-moment Region in Pre-stressed Continuous Composite Beam[J]. Water Resources and Power, 2013(12): 122-125 |
| [12] | 郑尚敏, 万水. 钢桁腹组合梁剪力滞效应的有限元分析[J]. 公路交通科技, 2013, 30(11): 68-72 ZHENG Shang-min, WAN Shui. Finite Element Analysis on Shear Lag Effect in Composite Girder with Steel Truss Webs[J]. Journal of Highway and Transportation Research and Development, 2013, 30(11): 68-72 |
| [13] | 孔令方, 邵旭东, 刘榕. 钢-UHPC轻型组合梁桥面板受弯性能有限元分析[J]. 公路交通科技, 2016, 33(10): 88-95 KONG Ling-fang, SHAO Xu-dong, LIU Rong. Finite Element Analysis of Flexural Performance of Steel-UHPC Lightweight Composite Girder Deck[J]. Journal of Highway and Transportation Research and Development, 2016, 33(10): 88-95 |
| [14] | 周志祥. 预应力钢桁-砼组合连续刚构桥梁及施工方法: 中国, v ZHOU Zhi-xiang. Prestressed Steel-concrete Composite Continuous Rigid Frame Bridge and Construction:China, ZL 200910104675. X[P].2012-07-04. |
| [15] | 周志祥. 预应力钢桁-砼组合连续刚构桥梁及施工方法: 德国, ZL 201310130786. 4[P]. 2012-07-04. ZHOU Zhi-xiang. The Shear Connectors of PCSS:Germany, ZL 201310130786.4[P]. 2012-07-04. |
| [16] | 李成君, 周志祥, 苏慈, 等. 预制装配式组合剪力钉试验研究[J]. 桥梁建设, 2015, 45(5): 60-65 LI Cheng-jun, ZHOU Zhi-xiang, SU Ci, et al. Experimental Study of Prefabricated Composite Shear Studs[J]. Bridge Construction, 2015, 45(5): 60-65 |
| [17] | 方秦, 还毅, 张亚栋, 等. ABAQUS混凝土损伤塑性模型的静力性能分析[J]. 解放军理工大学学报:自然科学版, 2007, 8(3): 254-260 FANG Qin, HUAN Yi, ZHANG Ya-dong, et al. Investigation into Static Properties of Damaged Plasticity Model for Concrete in ABAQUS[J]. Journal of PLA University of Science and Technology:Natural Science Edition, 2007, 8(3): 254-260 |
| [18] | JTG D62-2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62-2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
 2017, Vol. 34
2017, Vol. 34
