扩展功能
文章信息
- 李玉敏, 姚玉玲
- LI Yu-min, YAO Yu-ling
- 基于公路工程施工水平的定额测定对象选择方法
- A Quota Measurement Object Selection Method Based on Highway Construction Level
- 公路交通科技, 2017, 34(9): 45-51, 59
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(9): 45-51, 59
- 10.3969/j.issn.1002-0268.2017.09.007
-
文章历史
- 收稿日期: 2017-01-01
2. 中国葛洲坝集团公路运营有限公司, 湖北 武汉 430000
2. China Gezhouba Group Highway Operation Co., Ltd., Wuhan Hubei 430000, China
施工定额作为编制工程建设定额体系的基础,其直接反映生产技术水平和管理水平,为了保证其可靠性与实用性,编制时要遵循平均先进性的原则[1]。目前,我国在施工定额测定时,对所选测定对象的施工水平控制是采用规定正常施工条件,但是仅采用正常施工条件不能完全区别待选测定对象的施工水平,这对于定额测定要达到平均先进水平的贡献不足。基于这一现状,本研究从评价施工水平的角度出发,建立合理的施工水平评价指标体系,并采用有效的主客观结合的综合评价方法,对定额测定前可选的施工项目生产水平进行初步量化评价,且以此作为选择定额测定对象的依据,从而保证施工定额的水平。
当前在进行综合评价时权重系数的方法较多,按计算权系数时原始数据的不同来源分为主观赋权法与客观赋权法两类。总体来说,主观赋权法的客观性相对较差,但其因依据专家经验评定,解释性较强;客观赋权法是依据实际数据量化确定的权数,精确度比较高,但对所得结果难以给出明确的解释[2]。在经过综合考虑各种综合评价方法适用性的基础上,选取采用较成熟的改进层次分析法(IAHP)与粗糙集相结合的方式作为施工定额测定时施工水平的量化评价方法。
1 项目施工水平的影响因素对施工项目生产水平的评价离不开影响施工水平的生产因素,由于项目施工的复杂性与多变性,影响施工项目的生产水平因素有很多,本研究从测定施工定额的角度结合施工定额特定的测定方式以及我国项目施工模式,主要从项目部、施工班组、施工现场条件3方面来分析评价项目施工水平的影响因素。
(1) 体现施工企业施工与管理水平的主要是企业的资质等级,一般企业资质等级越高,相对应的技术人员的技术职称以及项目经理岗位资质就越高[3]。项目经理、项目总工和技术人员的资历以及学历决定项目部的管理水平;管理水平又直接决定工程施工组织方案的可行度、施工进度方案的可行度、施工组织中WPS分解的合理程度、材料采购跟进情况、材料摆放位置合理程度和机械的租赁等[4]。
(2) 施工班组是直接参与施工活动的一线人员,是直接决定施工快慢的主体,结合我国实行劳务分包与专业分包的大环境,分包班组管理水平、劳务公司信用评价、劳务公司资质等级对于施工班组的施工水平有着重要的影响。对于施工定额的测定来说,施工班组中劳动人员对工作的熟练程度,劳动人员的身体素质直接决定施工定额中人工的消耗量,即直接影响施工定额中劳动定额的水平。目前,随着施工机械化水平的提高,人工配合机械施工模式占主导,决定施工定额水平的是机械台班的消耗量,机械台班的消耗与机械自身的性能有关,但对于定额的测定来说,这一因素可以忽略,主要需要考虑的是同种机械在相似施工条件下的台班消耗,这就与机械对于现场条件的适用度、机械连续工作能力的变化情况,以及操作机械人员的技术熟练度、操作机械人员的年龄以及其身体状况、人机配合的默契度和机械的折旧程度等有关。
(3) 施工条件是影响施工水平的关键因素,通过对实际施工现场的调查发现,现场气候情况特征、地下水文情况、工地周边居民以及单位对施工影响的反馈情况、工人面对的施工对象的地质问题、现场材料运输的难易程度、现场交通情况、供水、供电情况、施工现场安全管理情况、现场附属物拆迁情况等都会对施工定额的水平产生一定的影响。
通过对上述所有影响因素进行分析,并结合专家分析论证选择其中对定额测定值可能产生主要影响的因素作为施工定额水平的评价指标。
2 评价指标体系的建立采用IAHP与粗糙集对施工定额水平进行综合评价时,需要建立相应的评价指标体系,本研究根据影响工程项目施工水平的因素以及选择测定对象的目的,建立了满足评价需求的三层次评价指标体系,具体为目标层、一级指标及二级指标。目标层为评价对象,是我们最终要评价的问题;一级指标是组成目标层的不同因素,二级指标是隶属于一级指标下影响各目标层的因素组合[5]。
为了便于评价二级指标,本研究在建立指标体系时,在充分考虑影响公路工程施工水平主要因素的同时,优先考虑采用可以明确评价的标准作为指标[6],使采用各评价指标评定项目时更清晰明确,也可提高采用粗糙集进行对象评定时的准确性。具体评价指标体系如图 1所示。

|
| 图 1 施工水平评价指标体系 Fig. 1 Construction level evaluation indicator system |
| |
3 IAHP评价指标权重的确定
自20世纪70年代提出以来,层次分析法(AHP)得到了较大的发展,目前,是一种应用较广泛的主观评价方法,IAHP(改进的层次分析法)是在AHP的基础上,将AHP法的重要度排序(1/9, 9) 标度以及权值计算优化,使排序者更容易确定其重要度,且无需再进行复杂的一致性检验。改进的层次分析法采用三标度,其权重的确定过程步骤如下[6-7]:
3.1 构造判断矩阵对建立的评价指标体系中同一层的各评价因素两两进行重要性的比较, 得到综合的比较矩阵, 再计算各指标重要程度排序指数,并根据其构造相应的判断矩阵。
(1) 采用式(1) 的量值规则来评判各评价因素的重要度,以此建立比较矩阵K:

|
(1) |
式中, Kij为因素i比因素j的重要程度的数量化值, 且Kii=1或Kjj=1。
(2) 计算重要性排序指数ri:
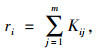
|
(2) |
式中, ri为矩阵K中第i行元素之和,取rmax=maxri,rmin=minri;
(3) 判断矩阵的计算公式如下:
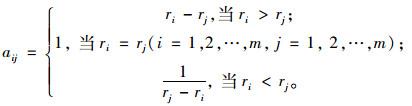
|
(3) |
式中,aij为矩阵的相应元素;ri为重要程度的排序指数;m为判断矩阵阶数。
3.2 计算判断矩阵的优化矩阵(1) 假定原判断矩阵为:A=(aij)m×m, 则按下列公式计算优化矩阵:

|
(4) |
优化矩阵为:
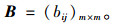
|
(5) |
(1) 计算各评价指标的单一权重值
各评价指标单一权重值的计算及归一化处理, 公式如下:
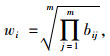
|
(6) |
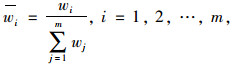
|
(7) |
式中, wi为第i个评价因素所对应的归一化的权重值;m为总的评价指标个数。判断矩阵通过上述计算可完成自协调优化, 得到的权值结果具有完全一致性。
(2) 计算各评价指标的综合权重值
设一级指标的权重为aj(j=1, 2, …, m), 二级指标i在一级某指标j下的权重为bij(i =1, 2, …, n), 其中m,n分别为一级指标和二级指标的总数目, 即二级指标i的综合权重计算公式为:
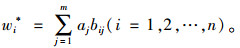
|
(8) |
最后根据所获得的二级指标权重值的大小决定各评价指标影响因素的大小, 为决策项目提供相应的理论依据。
通过问卷调查方式收集了50份现场施工技术人员以及施工定额测定方面的专家对指标体系中各影响因素重要程度打分情况,并按文中指标权重的确定方法得到一级指标权重的单一权重值如表 1所示,二级指标权重的单一权重值与综合权重值如表 2所示。
| 二级指标 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 |
| 单一权重 | 0.104 | 0.104 | 0.042 | 0.276 | 0.474 | 0.272 | 0.472 | 0.053 | 0.147 | 0.056 | 0.043 | 0.143 | 0.269 | 0.076 | 0.469 |
| 综合权重 | 0.059 | 0.059 | 0.024 | 0.158 | 0.271 | 0.078 | 0.135 | 0.015 | 0.042 | 0.016 | 0.006 | 0.020 | 0.038 | 0.011 | 0.067 |
4 粗糙集指标权重的确定 4.1 建立信息系统
(1) 定义[8-9]:设四元组合S=(U, A, V, f)为组成的信息系统。其中U为测定对象的有限非空集合,论域为:U={χ1,χ2,χ3,…,χn}; A为属性的有限非空集合, A={a1,a2,…,am},A中的每个aj(j≤m)为一个属性;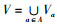
(2) 将上述图 1建立的评价指标中的所有二级指标作为信息系统的属性集合[10],即:
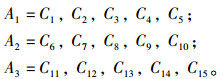
|
(3) 将要评价的各施工测定对象项目作为系统的对象集合,结合实际测定时项目的选择情况,在满足正常施工条件初始条件的所有项目中随机选择n个被评价的项目,且令U=U1, U2, U3, U4, U5, U6, U7…Un(U代表评价的测定对象集, U1~Un代表n个被评价的测定对象);评价时,将连续的数值离线赋值,定义图 1中二级指标的属性为“先进”、“平均”、“落后”3个等级[11],且分别用2,1,0来替代,从而得到离散化后的各信息系统S。
4.2 信息系统属性约简建立的信息系统中一般会存在无关分类的冗余属性,为了降低数据挖掘的处理难度,需要去除所有冗余属性,找到最小的不影响原始分类的属性集合[12],具体原理如下:
(1) 设∃一个信息系统S=(U, A, V, f),其中a∈A,若ind(A-{a})=indA,则认为a在A中是不必要的,可以约简,反之认为a在A中是必要的。
(2) 设∃一个信息系统S=(U, A, V, f),若对于∀a∈A在A中都是必要的,则认为属性集A是独立的,反之称A为相关的[13]。
(3) 如果A是独立的,且P ⊆A,则P也是独立的。
(4) 设∃一个信息系统S=(U, A, V, f),且P ⊆A,若P是属于独立的,并且indP=ind(A),则称P为A的一个约简。
(5) 设∃一个信息系统S=(U, A, V, f),将组成属性A的所有必要属性的集合称为属性集A的核,记为core(A)。
(6) core(A)=∩red(A), 其中red(A)表示A的所有约简。
核是所有约简的交集, 它包含于属性集A中的所有约简中,核是原始属性集合中最重要的属性子集,在要求对于原对象集合保持分类能力不减弱的前提下,核中的任何属性都不能被删掉[14]。
4.3 信息系统属性的重要性度量[8](1) 信息量定义
设S=(U, A, V, f)是一个信息系统,P⊆AU/ind(P)={X1, X2, …, Xn}。知识P的信息量定义为[9]:
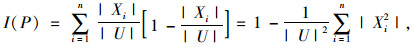
|
(9) |
式中,|X|表示集合X的基,即集合所包含的元素个数;|Xi|/|U|表示等价类Xi在U中的比例。
(2) 重要性度量方法
设S=(U, A, V, f)是一个信息系统,属性a∈A在A中的重要性定义为:
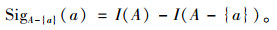
|
(10) |
当A=a时,用Sig(a)表示Sigφ(a):
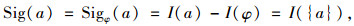
|
(11) |
式中,U/ind(φ)={U}, I(φ)=0。
上述表明,可以根据属性集A中去掉属性{a}后所导致的信息量变化的大小来度量a∈A在属性集A中的相对重要性。
4.4 基于粗糙集的指标权重确定设S=(U, A, V, f)是一个信息系统,A={a1,a2,…,am},属性ai∈A在A中的重要性为SigA-{ai}(ai),则ai∈A的权重定义为[9]:
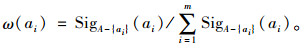
|
(12) |
(1) 设S=(U, A, V, f)是一个信息系统, ωsi,ωoi分别是属性ai主观权重和客观权重, ωi为两者的组合权重, 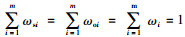
建立最优化模型:
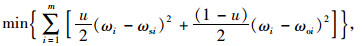
|
(13) |
式中ωi∈ψ= 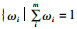
(2) 定理:最优化模型在可行域ψ上有唯一解, 且其解为:
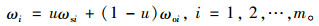
|
(14) |
证明 作Lagrange函数:
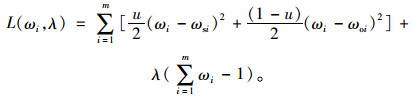
|
令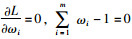
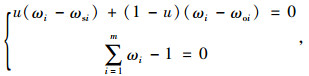
|
解此方程组得:
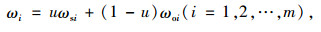
|
从而定理得证[16]。
(3) 将主观与客观的二级指标权重按黄金分割比进行分配,可得二级指标的组合权重。
5.2 基于组合权重的评价值公式(1) 评价值模型
定义:设ω(Aj)为IHAP法计算得到的一级指标权重,ω(aji)为约简后的信息系统中每个二级指标的组合权重,Fij为该测定对象在属性aij下的取值, 则每个对象的评价值计算公式如下:
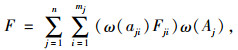
|
(15) |
式中n和mj分别表示约简后的信息系统中一级指标和二级指标的总个数[17]。
(2) 对象评价
根据指标权重以及每个对象在对应指标下取值, 可以计算出U中n个对象各自的评价值,评价值越大施工项目生产水平越高,施工定额测定人员可根据此评价值与评价排序来选择自身需求的项目施工水平来进行定额的测定[18]。
6 实例分析本研究在某施工企业能满足正常施工条件的所有施工项目中随机选择了7个项目作为被评价项目,令U=U1, U2, U3, U4, U5, U6, U7;对7个项目的二级指标评价打分后,得到各信息系统S,如表 3~表 5所示。
| C1 | C2 | C3 | C4 | C5 | |
| U1 | 2 | 2 | 2 | 1 | 2 |
| U2 | 2 | 2 | 2 | 2 | 2 |
| U3 | 2 | 2 | 2 | 2 | 2 |
| U4 | 1 | 1 | 1 | 2 | 1 |
| U5 | 1 | 2 | 1 | 1 | 1 |
| U6 | 2 | 2 | 2 | 2 | 1 |
| U7 | 1 | 1 | 1 | 1 | 2 |
| C6 | C7 | C8 | C9 | C10 | |
| U1 | 1 | 2 | 1 | 2 | 1 |
| U2 | 1 | 2 | 1 | 2 | 1 |
| U3 | 2 | 2 | 1 | 2 | 1 |
| U4 | 0 | 1 | 0 | 2 | 0 |
| U5 | 0 | 1 | 0 | 2 | 0 |
| U6 | 1 | 1 | 1 | 2 | 1 |
| U7 | 1 | 2 | 1 | 2 | 1 |
| C11 | C12 | C13 | C14 | C15 | |
| U1 | 2 | 2 | 1 | 1 | 2 |
| U2 | 2 | 1 | 2 | 1 | 2 |
| U3 | 1 | 2 | 1 | 1 | 2 |
| U4 | 0 | 1 | 2 | 1 | 2 |
| U5 | 0 | 2 | 1 | 2 | 2 |
| U6 | 1 | 2 | 1 | 2 | 2 |
| U7 | 1 | 1 | 1 | 1 | 2 |
根据上述离散化的信息表,得到论域在完整属性集下的分类情况和依次去掉一个属性后的分类情况,根据4.3,4.4节给出的计算方法计算各个属性集的信息量、重要性以及指标权重,以表 3为例计算过程如下:
(1) 信息量计算

|
(2) 重要性计算

|
(3) 指标权重计算
将属性的重要性按照如下公式归一化后就可以得到各属性的权重:
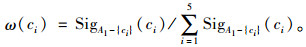
|
(16) |
最终得到的权重结果如表 6所示。
同理计算表 4、表 5可得各属性的权重结果如表 7、表 8所示。
将主观与客观的二级指标权重按黄金分割比进行分配,取U=0.382,计算可得二级指标的组合权重如表 9所示。
| 二级指标 | C4 | C5 | C6 | C7 | C11 | C12 | C14 |
| 层次分析法 | 0.368 | 0.632 | 0.366 | 0.634 | 0.164 | 0.546 | 0.290 |
| 指标权重法 | 0.5 | 0.5 | 0.5 | 0.5 | 0.6 | 0.2 | 0.2 |
| 组合权重 | 0.450 | 0.550 | 0.449 | 0.551 | 0.434 | 0.332 | 0.234 |
根据指标权重以及每个对象在对应指标下取值,按式(15) 计算出7个对象的评价值分别为:1.581,1.791,1.904,1.066,0.890,1.338,1.472,即实例选取的7个测定定额待选对象的施工生产水平排序为:U3>U2>U1>U7>U6>U4>U5,结果反映与实际施工生产水平较符合,施工定额测定人员可根据此评价值与评价排序来选择定额的测定对象。
7 结论(1) 测定对象所在项目施工水平直接影响测定的公路工程施工定额水平,在定额测定前,传统规定的正常施工条件不能直接体现对施工定额水平的要求。本研究提出的IAHP结合粗糙集确定定额测定对象水平的综合评价方法,弥补了主观评价的不足,使评价结果更可靠。
(2) 目前,我国关于定额测定施工水平评价指标的研究较少,本研究通过专家论证结合现场调研建立的施工水平评价指标体系,采用IAHP法利用专家打分得到各指标权重值,可直接作为施工定额测定对象的评价依据,对评价施工定额测定对象水平提供技术支持。
(3) 在定额测定前,将待选对象进行综合分析,通过评价值及各项目的施工水平排序,可剔除其中水平过高或水平过低的对象,选取符合施工定额水平要求的测定对象,为测定结果满足施工定额的平均先进水平要求提供较为科学可靠的保证。
| [1] | 石勇民. 公路工程定额原理与估价[M]. 北京: 人民交通出版社, 2004. SHI Yong-min. Principle and Valuation of Highway Engineering Quota[M]. Beijing: China Communications Press, 2004. |
| [2] | 杜栋, 庞庆华, 吴炎. 现代综合评价方法与案例精选[M]. 2版. 北京: 清华大学出版社, 2008. DU Dong, PANG Qing-hua, WU Yan. Modern Comprehensive Evaluation Method and Case Selection[M]. 2nd ed. Beijing: Tsinghua University Press, 2008. |
| [3] | 龙琰. 公路工程施工定额测定及原始数据处理方法研究[D]. 长沙: 长沙理工大学, 2007. LONG Yan. Study on Construction Quota Determination and Raw Data Processing Method for Highway Engineering[D]. Changsha:Changsha University of Science and Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10536-2007206215.htm |
| [4] | 胡建民. 企业劳动定额水平评定的几点新思考[J]. 机械管理开发, 1998(2): 53-55 HU Jian-min. Some New Thoughts on Evaluation of Enterprise Labor Quota Level[J]. Mechanical Management Development, 1998(2): 53-55 |
| [5] | 王首绪, 袁新杰. 基于AHP的公路工程施工定额测定现场筛选指标体系[J]. 长沙理工大学学报:自然科学版, 2012, 9(3): 15-18 WANG Shou-xu, YUAN Xin-jie. Selection Index System of Measured Scene of Highway Engineering Construction Quota Based on AHP[J]. Journal of Changsha University of Science and Technology:Natural Science Edition, 2012, 9(3): 15-18 |
| [6] | 张震. 基于层次分析法与模糊综合评价的供应商评价研究[J]. 东北大学学报, 2006, 27(10): 1142-1145 ZHANG Zhen. AHP-based Vendor Evaluation in Combination with FCE[J]. Journal of Northeastern University, 2006, 27(10): 1142-1145 |
| [7] | 陈沅江, 胡毅夫. IAHP法在公路施工环境综合评价中的应用研究[J]. 工业安全与环保, 2005, 31(11): 28-30 CHEN Yuan-jiang, HU Yi-fu. Study on the Application of the IAHP Method in Environmental Influence Comprehensive Evaluation in Highway Construction[J]. Industrial Safety and Environmental Protection, 2005, 31(11): 28-30 |
| [8] | PAWLAK Z. Rough Sets Theoretical Aspects of Reasoning about Data[M]. Boston: Kluwer Academic Publishers, 1991. |
| [9] | LEE J. Classification Based on Optimal Feature Extraction and the Theory of Rough Sets[D].San Diago:San Diego State University, 1994. |
| [10] | PAWLAK Z. Rough Sets Theory and Its Applications to Data Analysis[J]. Cybernetics and Systems, 1998, 29(1): 661-688 |
| [11] | 张文修, 吴伟志, 梁吉业, 等. 粗糙集理论与方法[M]. 北京: 科学出版社, 2001. ZHANG Wen-xiu, WU Wei-zhi, LIANG Ji-ye, et al. Rough Set Theory and Method[M]. Beijing: Science Press, 2001. |
| [12] | 刘保相. 粗糙集对分析理论与决策模型[M]. 北京: 科学出版社, 2010: 11-12. LIU Bao-xiang. Rough Set Pair Analysis Theory and Decision Model[M]. Beijing: Science Press, 2010: 11-12. |
| [13] | 梁吉业, 曲开社, 徐宗本. 信息系统的属性约简[J]. 系统工程理论与实践, 2001, 21(12): 76-80 LIANG Ji-ye, QU Kai-she, XU Zong-ben. Reduction of Attribute in Information Systems[J]. System Engineering-Theory and Practice, 2001, 21(12): 76-80 |
| [14] | 胡彧, 李智玲, 李春伟. 一种基于区分矩阵的属性约简算法[J]. 计算机工程与应用, 2006, 26(增1): 80-82 HU Yu, LI Zhi-ling, LI Chun-wei. Algorithm for Attribute Reduction Based on Discernibility Matrix[J]. Computer Engineering and Applications, 2006, 26(S1): 80-82 |
| [15] | 钟嘉鸣, 李订芳. 粗糙集与层次分析法集成的综合评价模型[J]. 武汉大学学报, 2008, 41(4): 126-130 ZHONG Jia-ming, LI Ding-fang. Comprehensive Evaluation Model Integrated Based on Rough Set and Analytic Hierarchy Process[J]. Engineering Journal of Wuhan University, 2008, 41(4): 126-130 |
| [16] | 姚珅, 高贵明. 层次-粗集组合赋权法在雷达辐射源识别中的应用[J]. 雷达与对抗, 2011, 31(2): 34-38 YAO Shen, GAO Gui-ming. The Application of Hierarchy-rough Set Combined Weight Assigning Method in Radar Radiation Source Recognition[J]. Radar & ECM, 2011, 31(2): 34-38 |
| [17] | LI Hua, LI De-yu, ZHAI Yan-hui, et al. A Novel Attribute Reduction Approach for Multi-label Data Based on Rough Set Theory[J]. Information Sciences, 2016, , S367-368: 827-847 |
| [18] | 张帆. 关于粗糙集的综合评价方法研究与应用[D]. 成都: 西南石油大学, 2015. ZHANG Fan. Research and Application of Comprehensive Evaluation Method of Rough Set[D]. Chengdu:Southwest Petroleum University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10615-1015605785.htm |
 2017, Vol. 34
2017, Vol. 34