扩展功能
文章信息
- 张向东, 李军, 曲直, 胡跃龙
- ZHANG Xiang-dong, LI Jun, QU Zhi, HU Yue-long
- 冻风积土的塑性损伤阈值及演化规律
- Study on Plastic Damage Threshold and Evolution Rule of Frozen Aeolian Soil
- 公路交通科技, 2017, 34(9): 37-44
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(9): 37-44
- 10.3969/j.issn.1002-0268.2017.09.006
-
文章历史
- 收稿日期: 2016-12-16
 )相关联流动法则并按照R-O硬化定律建立了冻风积土加载过程中塑性损伤演化模型(P模型)。利用文中提出的有效应力分析方法对试验所测得总动应变中所包含的累积塑性变形部分进行分离,实现了对P模型中参数拟合的目标;根据一、三主应力对D-P屈服边界进行划分以确定加载过程中弹塑性变形特征。通过分析裂隙发展规律研究冻风积土内部塑性损伤演化过程,将累积塑性变形变化率曲线的拐点作为冻风积土发生塑性损伤的阈值,给出了确定初始发生塑性损伤的理论依据。研究结果表明:P模型与相关文献模型确定的塑性损伤变量变化规律具有一致性,为冻风积土路基或基础的动力灾害防治研究提供理论基础。
)相关联流动法则并按照R-O硬化定律建立了冻风积土加载过程中塑性损伤演化模型(P模型)。利用文中提出的有效应力分析方法对试验所测得总动应变中所包含的累积塑性变形部分进行分离,实现了对P模型中参数拟合的目标;根据一、三主应力对D-P屈服边界进行划分以确定加载过程中弹塑性变形特征。通过分析裂隙发展规律研究冻风积土内部塑性损伤演化过程,将累积塑性变形变化率曲线的拐点作为冻风积土发生塑性损伤的阈值,给出了确定初始发生塑性损伤的理论依据。研究结果表明:P模型与相关文献模型确定的塑性损伤变量变化规律具有一致性,为冻风积土路基或基础的动力灾害防治研究提供理论基础。 ). By using the proposed effective stress analysis method, the cumulative plastic deformation part of the total strain measured is separated, and the target of the parameter fitting in the P model is realized. The D-P yield border is divided by 1st and 3rd principal stresses to determine the elastic and plastic deformation characteristics in the process of loading.By analyzing the rule of fracture development, the plastic damage evolution process in frozen aeolian soil is studied, the inflection point of the cumulative plastic deformation rate curve is taken as the threshold of the plastic damage of the frozen aeolian soil, and the theoretical basis for determining the initial occurrence of plastic damage is given. The result shows that the change of the plastic damage determined by P-model is consistent with that determined by the relevant literature model, which provided a theoretical basis for the study of the dynamic disaster prevention and control of frozen aeolian soil subgrade or foundation.
). By using the proposed effective stress analysis method, the cumulative plastic deformation part of the total strain measured is separated, and the target of the parameter fitting in the P model is realized. The D-P yield border is divided by 1st and 3rd principal stresses to determine the elastic and plastic deformation characteristics in the process of loading.By analyzing the rule of fracture development, the plastic damage evolution process in frozen aeolian soil is studied, the inflection point of the cumulative plastic deformation rate curve is taken as the threshold of the plastic damage of the frozen aeolian soil, and the theoretical basis for determining the initial occurrence of plastic damage is given. The result shows that the change of the plastic damage determined by P-model is consistent with that determined by the relevant literature model, which provided a theoretical basis for the study of the dynamic disaster prevention and control of frozen aeolian soil subgrade or foundation.
风积土在辽西地区具有广泛地分布,被大量用于地基或路基填土。地下水由于表面张力作用会在风积土颗粒间形成的孔隙通道中发生毛细上升现象,在寒冷冬季负温作用下会形成季节性冻土。主要承受的荷载一方面来自于行车冲击荷载或上部结构振动,另一方面是来自于地壳板块碰撞产生的地震作用。因此,研究冻土路基在动荷载作用下的力学特性及强度损伤机理对该类路基灾害防治具有重大意义。
对于岩土强度损伤问题,一大批国内外学者在损伤模型及损伤演化机理方面进行了大量研究。张超等[1]在深入探讨岩石压缩机理及变形过程基础上,建立了能反映损伤阈值影响的岩石单元强度度量方法与损伤演化模型。李栋伟等[2]基于Weibull分布建立了冻土蠕变损伤本构模型。刘增利等[3]利用CT观测技术对冻土在单轴压缩情况下的细观损伤发展过程进行测试。杨平等人[4]基于一系列假设建立了结构接触面循环剪切损伤模型。
冻土在循环荷载作用下,当荷载超过其屈服强度时会发生不可恢复的塑性变形,在微观角度上,冻土内部出现不可愈合的微裂隙。当冻土受到周而复始的循环荷载作用时,会发生疲劳损伤,这是导致塑性区发展的主要原因。随着塑性区进一步扩大,微裂隙也会进一步发展,直到冻土外部出现宏观裂隙发生破坏。因此,冻土强度损伤与冻土内部塑性区的发展有着密切的关系,根据累积塑性变形的发展规律来揭示冻土损伤机理是可行的。
控制塑性损伤发展对冻风积土承载能力起着至关重要的作用。传统的塑性损伤理论认为冻土一旦进入塑性区即发生塑性损伤,本研究认为冻风积土在进入塑性区后,累积塑性变形发展达到损伤阈值才产生塑性损伤,并给出损伤阈值确定方法。利用本研究提出的有效应力分析法对总动应变中的累积塑性变形部分进行分离,实现对P模型参数进行拟合,确定了不同条件下冻风积土塑性损伤的演化规律。
1 塑性损伤模型 1.1 屈服条件假定冻风积土发生的是理想弹塑性变形,在屈服过程中不产生体积膨胀,可以采用Drucker-Prager(D-P)屈服准则。在主应力空间中,冻风积土内部某一点发生屈服时,应力状态满足屈服函数f[5],即:
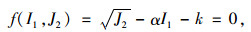
|
(1) |
式中,I1为第一主应力不变量;J2为第二偏应力不变量;α,k为由冻风积土黏聚力c和内摩擦角φ所确定的参数,可表示为:
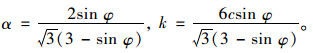
|
(2) |
假设冻风积土受到的围压相等(σ2=σ3)则D-P屈服准则可以退化成二维形式,见式(3),其对应的屈服边界为一偏心椭圆。
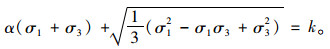
|
(3) |
根据弹塑性流动法则,假定冻风积土屈服面各点应力状态满足相关联流动法则,塑性应变变化量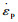
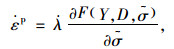
|
(4) |
式中,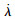
根据正交关系及式(4),参照文献[7]给出的Y形式,冻风积土的损伤状态方程为:
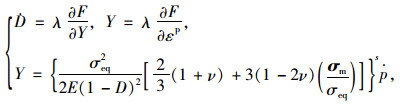
|
(5) |
式中,E为初始无损伤弹性模量;μ为泊松比;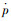
对于循环加载的冻土实际发生的是延性破坏,累积塑性应变率可表示为:
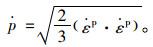
|
(6) |
若冻风积土发生的是各向同性损伤,可将耗散势函数F(Y, D, 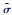
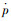
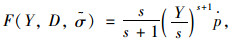
|
(7) |
式中s为依赖于温度的拟合参数。
根据式(7) 可得冻风积土损伤演化方程为:
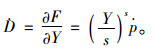
|
(8) |
由式(5) 和式(8),可得到损伤演化方程为:
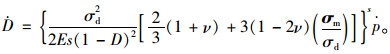
|
(9) |
根据Ramberg-osgood硬化定律[9],三向应力状态下的有效动应力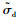
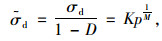
|
(10) |
式中,M,K为待拟合的硬化参数。
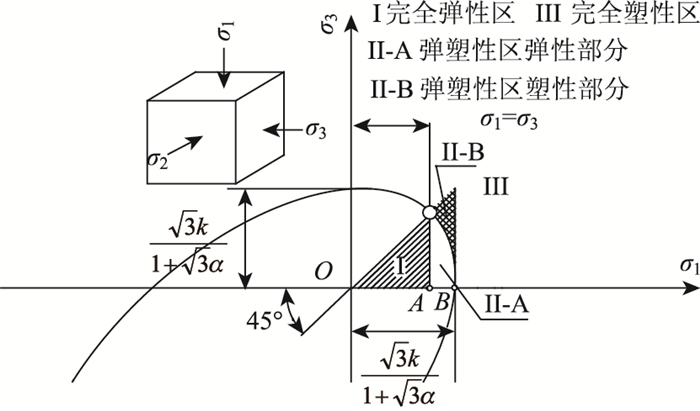
2 有效应力分析法冻风积土试样动应力σd与主应力间的关系为:σd=σ1-σ3,表示一系列与二四象限角分线平行的直线系。根据式(3),屈服边界为第一象限内的偏离原点的椭圆。根据σd将主应力空间划分为3个区域:完全弹性区(Ⅰ区)、弹塑性Ⅱ-A区、弹塑性Ⅱ-B区和完全塑性区(Ⅲ区),各区域划分的标准为:
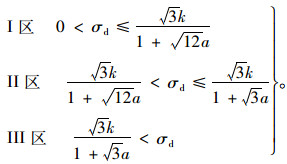
|
(11) |
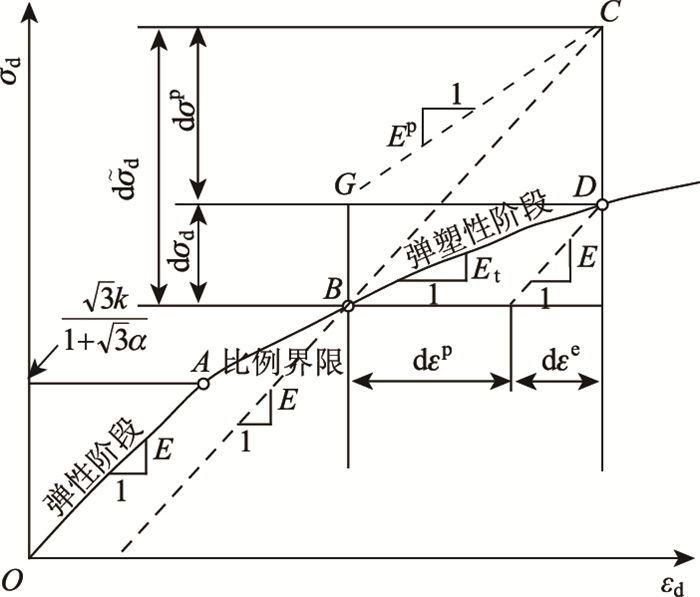
在图 1所示的σd-εd曲线上,可根据图 2所示的屈服准则中Ⅰ区和Ⅱ区分界点A确定比例界限,以该段的斜率作为初始弹性模量E。弹塑性阶段BD内发生的应变dεd可划分为塑性分量dεp和弹性分量dεe两部分。
|
| 图 1 有效应力法原理示意图 Fig. 1 Schematic diagram of effective stress method principle |
| |
|
| 图 2 屈服边界及应力区域划分示意图 Fig. 2 Schematic diagram of yield border and stress zoning |
| |
加载过程中,塑性应变εp会伴随总应变εd逐渐积累,从塑性损伤角度来看,这就是微损伤发展的过程。由损伤力学基本观点,冻土的损伤本构关系可以表示为:
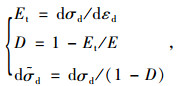
|
(12) |
式中,E为初始弹性模量;Et为dεd段内平均切线模量;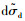
若在dεd线内发生的是线弹性变形,应力-应变曲线为直线BC,实际上,超过比例极限B点后发生的是有损伤的弹塑性变形,真实应力-应变曲线为BD。对于线弹性变形不考虑塑性损伤,本构关系为:
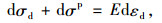
|
(13) |
式中,dσp为塑性应力形式,与动应变之间的关系可以表示为:
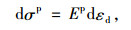
|
(14) |
式中,Ep为塑性变形切线模量,用dσd同时除以式(13) 等式两边,对照式(11) 可得:
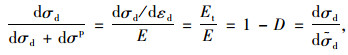
|
(15) |
式(15) 说明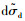
当σd超过比例极限点A后,虽然内部出现塑性区,但是仍以弹性变形为主。考虑到dεd=dεp+dεe及dεe=dεd/E及式(13) 的关系,将式(15) 代入到式(14) 中,整理可得:
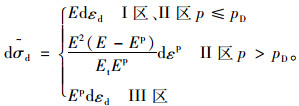
|
(16) |
由式(9)、式(10),冻风积土的塑性损伤动态演化方程为:
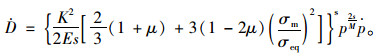
|
(17) |
塑性损伤动态演化方程的边界条件为:
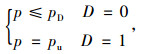
|
(18) |
式中,pD为塑性损伤的阈值;pu为因发生塑性损伤而导致失稳的阈值。
3 冻风积土动力特性测试 3.1 测试用土与设备试验采用英国生产的GDS冻土自动测试采集系统,该设备主要由加载系统、控制系统和数据采集分析系统组成,温度控制精度±0.1 ℃,最低负温-30 ℃,最大加载值10 MPa,满足试验要求。试验用土取自辽西阜新境内的人民桥附近的路基填土,带回实验室经过烘干、碾压、过筛的风积土样品分层碾压制成φ=31.9 mm, h=80 mm重塑土试样。在冷冻处理前抽真空保水2 h。将饱和的试样脱模并放入负温制冷装置中,使其在负温-20 ℃条件下静置48 h,待其达到恒温后进行动三轴试验。
现场取土相关操作及风积土参数测试符合《土工试验方法标准》的要求,利用室内土工试验测得取土的基本物理参数及颗粒筛分结果见表 1。
| 天然含水率 ω/% |
塑限ωp/% | 液限ωL/% | 塑性指数 Ip/% |
密度γ/ (kN·m-3) |
干密度γd/ (kN·m-3) |
孔隙比 | 黏聚力/kPa | 内摩擦角/ (°) |
| 22.2 | 18.1 | 29.4 | 11.3 | 21.2 | 16.8 | 0.632 | 19.5 | 30.2 |
3.2 测试方案
(1) 荷载选取
风积土路基在车辆荷载和地震荷载的影响下,其荷载可以等效为不同振幅、不同频率下的正弦波。研究表明[10],车辆振动荷载一般在10 Hz以下,本研究选用了2,4 Hz和8 Hz。根据负温对冻风积土强度的影响,最大轴向动应力σdmax一般选取单轴抗压强度qu的20%~80%[11]。实测该地区冻风积土试样在-10 ℃下的qu=3.5 MPa,本研究σdmax选为2.2 MPa;最小轴向动荷载σdmin选为0.7 MPa。以恒定频率、振幅递增的等效正弦波形式的荷载对冻风积土试样进行动力测试。
(2) 振动次数
采用逐级循环加载形式对冻风积土试样进行加载,通常每级荷载下的循环次数一般为2~10次。由于变形延迟特征,若振动次数过少,冻风积土在前一级荷载下变形尚未达到稳定就施加了下一级荷载;若振动次数太多,冻风积土会发生疲劳损伤,发生软化现象[12]。综合考虑,文中选为3次,如图 3所示。具体的试验方案见表 2。
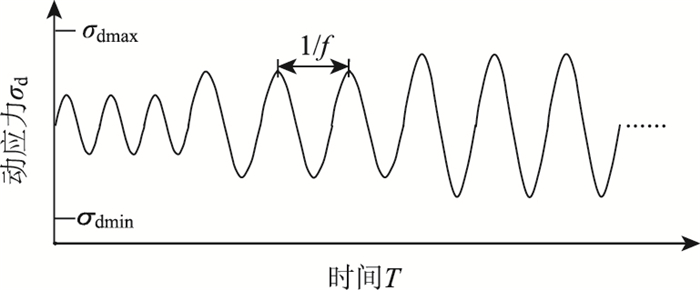
|
| 图 3 等效正弦波形示意图 Fig. 3 Schematic diagram of equivalent sine waveform |
| |
| 试验编号 | 影响因素 | ||
| 负温T/℃ | 围压/MPa | f/Hz | |
| 1 | -2 | ||
| 2 | -5 | 0.5 | 8.0 |
| 3 | -10 | ||
| 4 | 0.5 | ||
| 5 | -2 | 1.0 | 8.0 |
| 6 | 2.0 | ||
| 7 | 2.0 | ||
| 8 | -2 | 0.5 | 4.0 |
| 9 | 8.0 | ||
3.3 测试结果与分析
不同负温、不同围压和不同频率下,冻风积土的动应力-应变骨干曲线如图 4所示。

|
| 图 4 动应力-应变曲线 Fig. 4 Dynamic stress-strain curves |
| |
由图 4(a)可知,在σd较小的情况下,各负温条件下的动应力-应变曲线近似直线,发生弹性变形;当σd较大时,动应力-应变曲线偏离直线,并且偏离的程度越来越大,说明开始发生了塑性累积变形。温度越低,对应的比例极限σd越大,强度越高。温度越低,初始直线的斜率越大。
由图 4(b)可知,不同围压下的试样初始加载弹性模量相同。围压越高,比例界限所对应的动应变越大。这说明较高的围压可以提高冻风积土抵抗塑性变形的能力,延缓试样内部各点发生塑性变形。
由图 4(c)可知,试样具有相同的初始弹性模量,随着σd的增加试样逐渐进入塑性区。频率越大,对应的比例界限越小,说明较大加载频率使试样产生的疲劳加载损伤,提前使试样发生塑性变形。
4 塑性损伤分析随着循环次数增加,滞回曲线不闭合程度增加,产生塑性变形,见图 5。根据不同的动应力水平,变形可分为纯弹性、弹性安定、塑性安定和刺入破坏4种响应[13]。
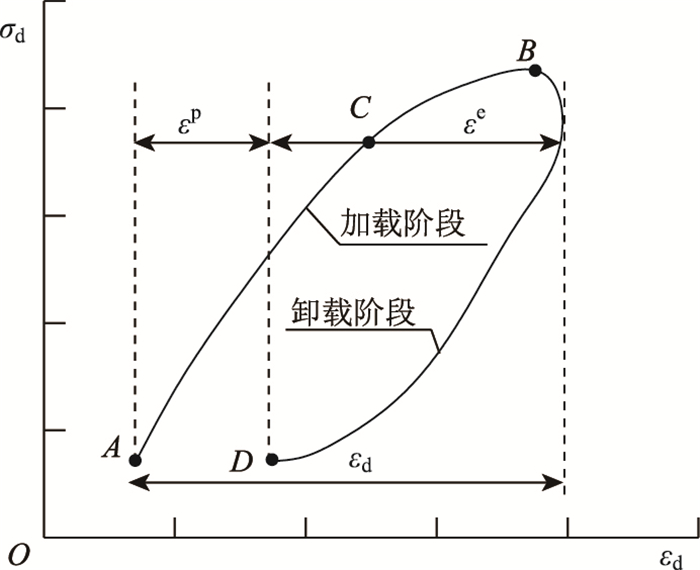
|
| 图 5 滞回圈及塑性变形示意图 Fig. 5 Schematic diagram of hysteresis circle and plastic deformation |
| |
4.1 塑性损伤阈值分析原理
由于冻风积土发生的塑性损伤与裂隙的发展有直接联系,因此,可按照裂隙的发展过程将全过程动应力-动应变曲线分为Ⅰ~Ⅴ共5个阶段,如图 6所示。
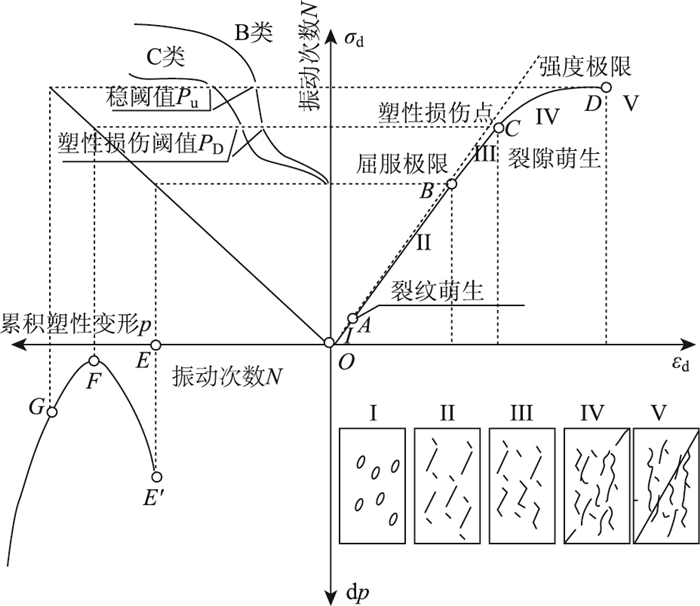
|
| 图 6 塑性损伤阈值分析原理图 Fig. 6 Plastic damage threshold analysis principle diagram |
| |
从裂纹开始产生继而发展,累积塑性变形率不断地增加。随着加载,冻风积土试样的横截面积会不断变大,塑性变形发展减慢,当进入到裂纹损伤阶段后,累积塑性变形率会减小。所以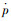
Ⅰ——裂隙闭合阶段(OA):该阶段动应力-应变曲线上凹,这主要是冻风积土内部初始裂隙在荷载作用下出现闭合的缘故,尤其在高围压作用时上凹现象比较明显。其次,这种现象还与冻风积土内部土颗粒不均匀及裂隙不均匀分布有关[15];
Ⅱ——线弹性变形阶段(AB):该阶段在外荷载作用下裂隙会进一步减小,虽然发生部分不可恢复的变形,但是线弹性变形仍然占据变形主要特征,直到裂隙萌生点B点发生屈服,加载曲线偏离直线;
Ⅲ——裂纹发展阶段(BC):超过B点后,原生裂纹及新产生裂纹继续发展相互连通,形成裂纹,骨架开始发生屈服,塑性变形开始累积,直到C点开始发生塑性损伤,累积塑性变形率急剧加快,动应力-应变曲线出现拐点,即为塑性损伤阈值pD;
Ⅳ——塑性损伤发展阶段(CD):超过C点后,冻风积土内部塑性累积变形造成塑性损伤发展,损伤后动应力-应变曲线非线性特征更加明显,塑性累积变形开始急剧加快,直到D点丧失稳定性,不再具有承载能力;
Ⅴ——失稳阶段(D点以后):此阶段裂纹急剧发展扩充,形成了贯穿于冻风积土表面的宏观裂隙,丧失继续承载的能力。
加载过程中,σd超过屈服极限后的塑性变形可根据图 1所示的原理图来确定。累积塑性变形p可根据式(7) 来计算。各条件下的p与循环次数间的关系如图 7所示。塑性变形发展都经历了从加速阶段到稳定阶段的过程。在温度降低、围压升高以及频率降低的情况下塑性变形发展缓慢。这说明围压、负温对冻风积土的强度损伤具有抑制作用;提高频率,加快了疲劳损伤,对冻土强度的损伤具有促进作用[16]。
|
| 图 7 不同条件下的累积塑性应变曲线 Fig. 7 Cumulative plastic strain curves under different conditions |
| |
由式(1)、式(2) 可知,冻风积土的屈服极限是依赖于抗剪强度指标c,φ的,假设内部各点的均一稳定特征,各条件下的c,φ值以及按照图 6所示的分析原理所确定的塑性损伤阈值见表 3。
| 试验编号 | c/MPa | φ/(°) | α/(×10-3) | k/(×10-3) | pD/% |
| 1 | 0.231 | 0.56 | 3.77 | 2.61 | 0.52 |
| 2 | 0.796 | 0.43 | 2.89 | 6.91 | 0.86 |
| 3 | 1.853 | 0.27 | 1.82 | 10.09 | 1.72 |
| 4 | 0.265 | 0.57 | 3.75 | 2.67 | 0.84 |
| 5 | 1.734 | 0.52 | 3.50 | 8.22 | 1.02 |
| 6 | 1.829 | 0.46 | 3.10 | 16.99 | 1.51 |
| 7 | 0.286 | 0.55 | 3.76 | 2.63 | 0.91 |
| 8 | 1.816 | 0.65 | 3.07 | 7.76 | 0.76 |
| 9 | 2.016 | 0.68 | 2.84 | 17.21 | 0.37 |
4.2 塑性损伤演化规律
目前对有影响的参数s研究甚少,文中选定s为1[17]。根据图 1所示的有效应力
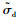
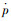
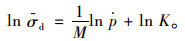
|
(19) |
拟合直线的斜率为1/M,截距为ln K,参数M,K得以确定。拟合结果见表 4。
| 编号 | E/MPa | σm | M | K | 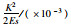 |
R2 |
| 1 | 127.36 | 0.51 | 1.62 | 0.53 | 1.10 | 0.97 |
| 2 | 135.91 | 0.53 | 1.33 | 0.54 | 1.07 | 0.99 |
| 3 | 167.26 | 0.52 | 0.86 | 0.57 | 0.97 | 0.98 |
| 4 | 135.32 | 0.62 | 1.27 | 0.68 | 1.71 | 0.97 |
| 5 | 116.41 | 0.63 | 1.16 | 0.57 | 1.40 | 0.99 |
| 6 | 113.27 | 0.57 | 1.08 | 0.52 | 1.19 | 0.98 |
| 7 | 145.36 | 0.36 | 1.28 | 0.31 | 0.33 | 0.98 |
| 8 | 121.24 | 0.42 | 1.06 | 0.29 | 0.35 | 0.99 |
| 9 | 117.31 | 0.37 | 0.84 | 0.27 | 0.31 | 0.98 |
考虑边界条件式(18),对式(17) 进行积分, 可得塑性损伤演化方程(P模型)为:
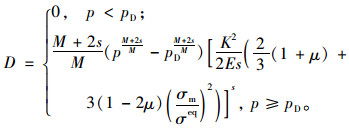
|
(20) |
当p>pD时,P模型中损伤变量D随着p的增加而逐渐演化,为了验证P模型是否具有合理性,将P模型计算结果与文献[18]塑性损伤模型计算结果进行对比,对比结果如图 8所示。
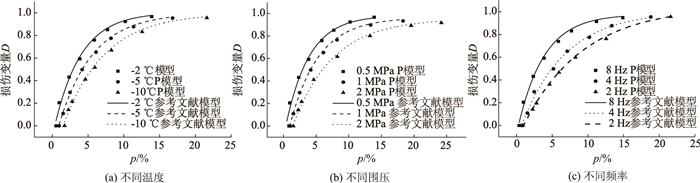
|
| 图 8 不同条件下损伤模型计算值对比 Fig. 8 Comparison of damage model calculated values under different conditions |
| |
理论上当p→∞时,D→1,因此塑性损伤演化曲线应逐渐衰减,最终以D=1为渐近线。P模型与文献[18]中损伤模型均验证了冻土塑性损伤具有衰减特征,并且P模型给出了塑性损伤阈值确定方法。当p较小时,二者差异不大,当p增加时,二者间出现了一定的偏差,P模型计算的损伤值比参考文献[18]损伤模型计算的损伤值偏小。因此,按照有效应力分析方法分离出来的塑性分量对所建立的P模型进行参数拟合,并将该模型用于描述冻风积土塑性损伤演化特征的研究方法更为合理。
5 结论通过开展动三轴试验获取冻风积土动应力-应变骨干曲线,利用有效应力原理对加载过程中产生的累积塑性变形进行分离,并对P模型进行参数拟合,获得了如下结论:
(1) 通过动荷载对冻风积土弹塑性变形区域进行划分,采用有效应力分析方法拟合的参数M,K可以使P模型较好地描述冻风积土在循环加载发生动力损伤条件下的应力-应变关系。
(2) 造成冻风积土发生强度损伤的主要原因是塑性变形p不断积累,当p达到pD时开始发生塑性损伤,直到pu丧失承载能力。依据文中提出的塑性损伤阈值分析方法所确定的9组试验中,最小的阈值为0.52%,最大的阈值为1.72%。
(3) P模型与其他相关文献模型确定的损伤具有相似规律,在数值上也比较接近,并且该模型给出明确的损伤阈值确定方法。因此,用P模型来研究冻风积土塑性损伤演化规律较为合理。
| [1] | 张超, 展旭财, 杨春和. 粗粒料强度及变形特性的细观模拟[J]. 岩土力学, 2013, 34(7): 2077-2083 ZHANG Chao, ZHAN Xu-cai, YANG Chun-he. Mesoscopic Simulation of Strength And Deformation Characteristics of Coarse Grained Materials[J]. Rock and Soil Mechanics, 2013, 34(7): 2077-2083 |
| [2] | 李栋伟, 汪仁和, 范菊红. 白垩系冻结软岩非线性流变模型试验研究[J]. 岩土工程学报, 2011, 33(3): 398-403 LI Dong-wei, WANG Ren-he, FAN Ju-hong. Nonlinear Rheological Model for Frozen Soft Rock during Cretaceous Period[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3): 398-403 |
| [3] | 刘增利, 张小鹏, 李洪升. 基于动态CT识别的冻土单轴压缩损伤本构模型[J]. 岩土力学, 2005, 26(4): 542-546 LIU Zeng-li, ZHANG Xiao-peng, LI Hong-sheng. A Damage Constitutive Model for Frozen Soils under Uniaxial Compression Based on CT Dynamic Distinguishing[J]. Rock and Mechanics, 2005, 26(4): 542-546 |
| [4] | 杨平, 赵联桢, 王国良. 冻土与结构接触面循环剪切损伤模型[J]. 岩土力学, 2016, 37(5): 1217-1223 YANG Ping, ZHAO Lian-zhen, WANG Guo-liang. A Damage Model for Frozen Soil-structure Interface under Cyclic Shearing[J]. Rock and Soil Mechanics, 2016, 37(5): 1217-1223 |
| [5] | YANG Q, THAM L G, SWOBODA G. Basis of Non-linear Phenomenological Equations as Damage Evolution Laws[J]. Mechanical Research Communications, 2002, 29(2): 131-136 |
| [6] | 李兆霞. 损伤力学的理论与应用[M]. 北京: 科学出版科学出版社, 2002. LI Zhao-xia. Theories and Application of Damage Mechanics[M]. Beijing: Science Press, 2002. |
| [7] | DHAR S, DIXIT P M, SETHURAMAN R A. Continuous Damage Mechanics Model for Ductile Fracture[J]. International Journal of Pressure Vessels & Piping, 2000, 77(6): 335-344 |
| [8] | LUO X, LUO T, WU X, et al. Constitutive Model of Frozen Soil[J]. Industrial Construction, 2014, 37(4): 811-816 |
| [9] | HAYKAWA K, MURAKAMI S, LIU Y. An Irreversible Thermo Dynamics Theory for Elastic-plastic-damage Materials[J]. European Journal of Mechanics-A/Solids, 1998, 17(1): 13-32 |
| [10] | 张锋. 深季节冻土区重载汽车荷载下路基动力响应与永久变形[D]. 哈尔滨: 哈尔滨工业大学, 2012. ZHANG Feng. Dynamic Response and Permanent Deformation of Subgrade Induced by Heavy Truck Load in Deep Seasonally Frozen Region[D].Harbin:Harbin Institute of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10213-1012024332.htm |
| [11] | 程学磊, 李顺群, 孙世娟, 等. 围压和负温对冻土强度和微结构的影响研究[J]. 广西大学学报:自然科学版, 2014, 39(1): 95-104 CHENG Xue-lei, LI Shun-qun, SUN Shi-juan, et al. Effect of Confining Pressure and Negative Temperature on Strength and Microstructure of Frozen Soil[J]. Journal of Guangxi University:Natural and Science Edition, 2014, 39(1): 95-104 |
| [12] | 任廷鸿. 冲击载荷下疲劳损伤力学及锻锤基础的疲劳损伤分析[D]. 杭州: 浙江大学, 2006. REN Ting-hong. Analysis of Fatigue Damage Mechanics under Impact Load and Fatigue Damage of Hummer-foundation[D].Hangzhou:Zhejiang University, 2006. http://cdmd.cnki.com.cn/article/cdmd-10335-2007015463.htm |
| [13] | 姚兆明, 陈晓霞. 长期循环荷载下饱和软粘土安定性模型[J]. 土木建筑与环境工程学报, 2011, 33(3): 31-35 YAO Zhao-ming, CHEN Xiao-xia. Shakedown Model for Saturated Clay Behavior under Long-term Cyclic Loading[J]. Journal of Civil Architectural & Environmental Engineering, 2011, 33(3): 31-35 |
| [14] | 关虓, 牛荻涛, 王家滨, 等. 考虑塑性应变及损伤阈值的混凝土冻融损伤本构模型研究[J]. 防灾减灾工程学报, 2015, 35(6): 777-784 GUAN Xiao, NIU Di-tao, WANG Jia-bin, et al. Study on Freeze-thaw Damage Constitutive Model of Concrete Considering Plastic Strain and Damage Threshold[J]. Journal of Disaster Prevention and Mitigation Engineering, 2015, 35(6): 777-784 |
| [15] | 张向东, 李庆文, 李广华, 等. 原状非饱和风积土的结构性参数与强度指标关系的试验研究[J]. 公路交通科技, 2016, 33(1): 41-48, 56 ZHANG Xiang-dong, LI Qing-wen, LI Guang-hua, et al. Experimental Research on Relationship of Structural Parameters with Structural Strength Indexes of Intact Unsaturated Aeolian Soil[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 41-48, 56 |
| [16] | 任廷鸿, 张我华, 薛新华. 冲击载荷作用下土的疲劳损伤特性分析[J]. 水利学报, 2014, 45(5): 619-625 REN Ting-hong, ZHANG Wo-hua, XUE Xin-hua. Study on the Fatigue Damage Properties of Foundation Soil under Impact Loading[J]. Journal of Hydraulic Engineering, 2014, 45(5): 619-625 |
| [17] | 唐雪松, 郑健龙, 蒋持平. 连续损伤理论与应用[M]. 北京: 人民交通出版社, 2005: 1-8. TANG Xue-song, ZHENG Jian-long, JIANG Chi-ping. Continuum Damage Theory and Application[M]. Beijing: China Communications Press, 2005: 1-8. |
| [18] | 孙星亮, 汪稔, 胡明鉴. 冻土弹塑性各向异性损伤模型及其损伤分析[J]. 岩石力学与工程学报, 2005, 24(19): 119-123 SUN Xing-liang, WANG Ren, HU Ming-jian. An Elastoplastic Anisotropic Damage Model for Frozen Soil and Its Damage Analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(19): 119-123 |
 2017, Vol. 34
2017, Vol. 34
