扩展功能
文章信息
- 何忠明, 邓喜, 付宏渊, 曾铃
- HE Zhong-ming, DENG Xi, FU Hong-yuan, ZENG Ling
- 降雨工况下渗透力对粗粒土高路堤边坡稳定性的影响
- Influence of Seepage Force on Stability of Coarse Grained Soil High Embankment under Rainfall Condition
- 公路交通科技, 2017, 34(9): 14-21, 29
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(9): 14-21, 29
- 10.3969/j.issn.1002-0268.2017.08.003
-
文章历史
- 收稿日期: 2016-10-24
2. 长沙理工大学 交通运输 工程学院, 湖南 长沙 410114;
3. 长沙理工大学 土木与建筑学院, 湖南 长沙 410114
2. School of Transportation Engineering, Changsha University of Science and Technology, Changsha Hunan 410114, China;
3. School of Civil Engineering and Architectural, Changsha University of Science & Technology, Changsha Hunan 410114, China
粗粒土(粒径在0.075 mm≤d0≤60 mm范围内的质量占试样总质量的50%以上[1])因其具有孔隙率大、透水性强、抗压强度高、压实密度大等工程特性,在湖南高速公路高路堤的填筑施工中已得到广泛应用。但是根据陈晓斌[2]的调研结果可知,在湖南多雨地区,已运营的高速公路粗粒土高路堤边坡受降雨影响灾变明显。近年来广大学者针对降雨工况下,渗透力致使边坡失稳问题,做了一些研究:如李广信[3]指出了土骨架和渗透力的定义,为降雨入渗过程粗粒土骨架受力分析提供了理论依据。陈祖煜[4]提出并论证了在计算边坡稳定性时,采用水、土合算,水、土分算两种方法得到的结果较为一致,也从侧面反映了以粗粒土骨架为研究对象来分析渗透力对边坡稳定性影响方法的可行性。连继峰,刘子振,付宏渊等[5-8]分析了渗透力、有效应力作用下,降雨入渗对边坡稳定性影响。宋子亨,马年祖[9-10]研究发现基质吸力的存在对土体抗剪强度具有一定提高。综上所述,现有学者关于渗透力对边坡稳定性影响的有限元分析方面尚存在一些不足:一方面,重复考虑了孔隙水压力变化和渗透力对边坡稳定性的影响;另一方面,单一考虑静孔隙水压力、基质吸力变化对边坡稳定性的影响,不能完全反映雨水在边坡内部入渗过程中,渗透力作用方向对边坡稳定性的影响,尤其是对于透水性强的粗粒土,渗透力对粗粒土骨架力学性能影响更为明显。
因此,针对湖南地区的气候特点,以粗粒土骨架为研究对象,基于饱和-非饱和理论,采用seep模拟粗粒土高路堤边坡降雨工况下的渗流特性;应用FLAC3D中的fish语言将渗透力以体力的方式施加在边坡各节点上,分析水位线升降、基质吸力变化、重度变化影响下,渗透力对粗粒土高路堤边坡安全系数变化以及塑性区分布规律的影响,可为粗粒土高路堤边坡设计提供指导。
1 边坡渗流特性及稳定性分析理论 1.1 饱和-非饱和渗流理论粗粒土高路堤边坡的渗流问题,满足达西定律土体内非恒定渗流,其偏微分方程形式如式(1) 所示[10]:
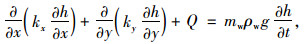
|
(1) |
式中,h为土体中的总水头;kx和ky为x和y方向的渗透系数;Q为源汇项;mw为比水容量;ρw为水的密度;g为重力加速度;t为时间。
非恒定渗流的初始条件为[11]:

|
(2) |
有限元方程求解可结合以下边界条件求解:

|
(3) |

|
(4) |
式中,S1为已知水头边界;S2为已知流量边界。
在缺乏试验成果的情况下,可采用经典的Van Genuchten模型,拟合粗粒土高路堤边坡的土水特征曲线。模型表达式为[12]:

|
(5) |

|
(6) |
式中,θ为土壤体积含水率;h为压力水头;θs和θr分别为粗粒土饱和体积含水量与残余体积含水量;α和n为经验拟合参数(或曲线形状参数),而m=1-1/n;Ks为饱和渗透系数;K(θ)为渗透系数随坡体内体积含水率的变化关系。
1.2 渗透力计算渗透力是指粗粒土高路堤边坡在降雨入渗过程中,雨水在坡体内部流动对粗粒土骨架所施加的力;渗透力除了拖曳力外,还有沿流向的巨大压力差[3]。因此仅通过研究降雨入渗前后静孔隙水压力变化,不能真正反映雨水入渗过程中,渗透力对边坡稳定性的影响。降雨入渗过程中雨水对粗粒土骨架作用效果如图 1所示。

|
| 图 1 渗透力作用示意图 Fig. 1 Schematic diagram of seepage force |
| |
渗透力计算如式(7)、(8) 表示[13]。由于边坡渗流过程中,内部渗流路径极为复杂且难以确定,因此文中采用geo-studio软件中的seep模块,模拟粗粒土高路堤边坡渗流过程中x,y两方向的渗流梯度;再将x,y两个方向渗流梯度乘以相应的水重度(γw),通过fish语言导入到FLAC3D中,其中渗透力的方向为x,y两个力合力的方向。

|
(7) |

|
(8) |
式中,F为渗透力; γw为水的重度; j为水力梯度; 
法国著名科学家库仑于1776年根据抗剪强度试验提出土的抗剪强度τf计算公式[14]:

|
(9) |
式中,c为黏聚力;σ′为剪切滑裂面的有效正应力;φ为内摩擦角。由于式(9) 仅考虑了饱和状态下土体的抗剪强度,未考虑非饱和状态下基质吸力对边坡稳定性的贡献,据此Fredlund等[15]根据非饱和土的双应力变量(σ-μa,μa-μw)理论提出了非饱和抗剪强度公式:

|
(10) |
式中,μa为边坡土体的进气值,由于考虑边坡孔隙与大气相连,μa =0;φb为基质吸力对内摩擦角的贡献,按经验取值φb=14°;μw为孔隙水压力。
1.4 边坡稳定性分析方法在边坡稳定性分析过程中,由于FLAC3D软件在边坡渗流计算时,软件会将负孔隙水压力全部归零,故在使用FLAC3D软件分析边坡流固耦合问题时,不能考虑基质吸力对粗粒土高路堤边坡稳定性的影响。因此,为充分反映雨水入渗过程中渗透力对边坡稳定性的影响,以粗粒土骨架为研究对象,采用geo-studio软件的seep模块计算边坡的渗流特性,然后将渗透力导入到FLAC3D中计算粗粒土高路堤边坡稳定性。
根据渗透力定义可知,渗透力是由水头损失产生,故当以粗粒土骨架为研究对象时,可仅考虑渗透力对边坡稳定性影响,不再重复考虑正孔隙水压力变化对边坡稳定性的影响。当以粗粒土骨架为研究对象,粗粒土骨架的静力平衡方程如式(11)、(12) 所示。边坡稳定性计算的具体流程图如图 2所示。

|
(11) |

|
(12) |

|
| 图 2 路堤边坡稳定性计算流程 Fig. 2 Calculation process of embankment slope stability |
| |
式中,Ga为粗粒土骨架水上部分自重;G′b为粗粒土骨架水下部分浮重;τ为粗粒土骨架抗剪强度;F为粗粒土骨架所受渗透力合力;γs为粗粒土饱和重度;γw为水的重度;V为水位线以下粗粒土体积。
2 边坡计算条件 2.1 计算模型粗粒土高路堤边坡依托工程位于湖南省郴州地区,起点桩号为K10+320,边坡高度为20 m。边坡分为两级,第1,2级边坡高度分别为8,12 m,坡率分别为1:1.5,1:1.75,降雨入渗过程如图 3所示。利用geo-studio软件中的seep模块建立相应的计算模型,为方便观察边坡表层基质吸力变化规律,在边坡坡面以下2 m布置5个监测点。计算模型如图 4所示,总节点数为5 124个,单元个数为3 228个。

|
| 图 3 降雨入渗过程 Fig. 3 Process of rainfall infiltration |
| |

|
| 图 4 路堤边坡有限元网格划分 Fig. 4 Finite element meshing of embankment slope |
| |
边界条件:坡脚左侧以及坡面为降雨入渗边界,边坡坡顶为封闭道路,设置为不透水边界,边坡底部设置为不透水边界。
2.2 计算参数查阅郴州地区气象资料可知,郴州历史上最大连续3日降雨量为357 mm。因此,文中考虑极端降雨工况下粗粒土高路堤边坡的稳定性,取降雨强度为1.38×10-6 m/s,通过室内试验,郴州地区粗粒土高路堤在标准压实度下饱和体积含水率为0.12,残余体积含水率为0.08,饱和渗透系数为1.02×10-6 m/s,并假设粗粒土高路堤填料为各向同性材料。由于通过室内试验测定粗粒土的土水特征曲线具有较大困难,故采用Van Genuchten模型拟合粗粒土渗透系数、体积含水率随基质吸力的变化规律;根据现有研究成果,粗粒土路堤边坡最大基质吸力不超过100 kPa,因此渗流分析过程中设置初始最大基质吸力为60 kPa[16]。拟合后的Van Genuchte关系曲线如图 5、图 6所示。

|
| 图 5 x方向渗透系数随基质吸力变化关系 Fig. 5 Relationship between permeability coefficient and matrix suction in x direction |
| |

|
| 图 6 含水率随基质吸力变化规律 Fig. 6 Relationship between water content and matrix suction in x direction |
| |
通过室内筛分试验、查阅相关文献、物理力学参数试验可知,郴州地区粗粒土的级配曲线变化关系如图 7所示,计算选用的粗粒土高路堤边坡的相关参数如表 1所示[17-18]。

|
| 图 7 粗粒土级配曲线 Fig. 7 Grading curves of coarse grain soil |
| |
| 岩性 | 饱和重度 γsat/ (kN·m-3) |
干重度 γd/ (kN·m-3) |
有效黏聚力c/ kPa |
有效内摩擦角 φ/(°) |
变形模量E/ MPa |
φb/ (°) |
泊松比μ |
| 粗粒土 | 22 | 19 | 35 | 32 | 25 | 14 | 0.35 |
由图 7可知,研究区内0.075 mm≤d0≤20 mm约占总量的55%,黏土含量为45%。
3 计算结果分析 3.1 边坡降雨入渗水位线分布规律图 8为粗粒土高路堤边坡降雨过程中和降雨停止后边坡的水位线变化规律。

|
| 图 8 高路堤边坡地下水位线分布规律 Fig. 8 Distributions of underground water table of high embankment |
| |
由图 8可知,降雨过程中粗粒土高路堤边坡首先在坡脚处到达饱和,并且随降雨历时增加,粗粒土高路堤边坡水位线逐渐抬升,当降雨历时60 h时,边坡水位线高度达到第1级平台坡脚处;此外,靠近边坡坡面处的水位线抬升速度明显快于道路中心线附近的水位线抬升速率;降雨停止后,边坡水位线逐渐下降,并且靠近边坡坡面处的水位线下降速率明显快于远离边坡坡面处的水位线下降速率。产生上述现象的原因为:粗粒土高路堤边坡采用Van Genuchten模型拟合渗透系数、体积含水率随基质吸力的变化关系,在Van Genuchten模型中渗透系数和体积含水率随基质吸力的增加逐渐减小,在坡脚处基质吸力较小,所以渗透系数较大,雨水入渗量较多,先达到饱和;随着降雨历时的增加,边坡坡面附近逐渐形成暂态饱和区, 渗透系数明显大于道路中心线附近的渗透系数,所以靠近坡面处的水位线抬升速率明显快于道路中心线附近的水位线抬升速率。
3.2 边坡降雨入渗基质吸力分布规律降雨过程中,边坡坡面监测点的基质吸力变化规律如图 9所示。

|
| 图 9 降雨过程中边坡监测点孔隙水压力分布规律 Fig. 9 Distribution of pore water pressure at measuring points during rainfall |
| |
由图 9可知,随降雨历时增加边坡基质吸力(即负孔隙水压力)逐渐消散并转变为正孔隙水压力,降雨停止后边坡内部正孔隙水压力逐渐减小,基质吸力逐渐恢复;此外,初始条件下监测点距离边坡水位线越近,其孔隙水压力越大。产生上述现象的原因为:随着降雨历时增加,粗粒土高路堤边坡内部水位线抬升,边坡坡面附近形成暂态饱和区,孔隙被入渗的雨水填充,最终基质吸力消散,转变为正孔隙水压力并逐渐增大;降雨停止后,雨水从边坡内部排出,基质吸力逐渐恢复。
3.3 边坡降雨入渗渗流速度分布规律根据渗透力定义可知,雨水入渗过程中渗流速度矢量大小及分布规律直接反映渗透力分布规律。因此,为揭示降雨过程中,入渗的雨水在粗粒土高路堤边坡中的渗流规律以及渗透力的分布规律,给出降雨24,72 h的渗流速度矢量分布,如图 10所示。

|
| 图 10 速度矢量分布规律 Fig. 10 Distribution of velocity vector |
| |
由图 10可知,0~24 h内降雨入渗主要分布在边坡坡脚以及边坡坡面表层附近,速率分布的面积较小,降雨72 h时雨水逐渐向边坡内部转移且降雨过程中部分雨水速度矢量指向坡面。产生上述现象的原因为:降雨0~24 h内坡脚先达到饱和,雨水主要汇聚在坡脚处,渗透系数较大,所以速度矢量主要分布在坡脚及边坡坡面表层附近;随降雨历时的增加,水位线逐渐抬升,暂态饱和区的面积逐渐增大,渗透系数逐渐增大,此外部分入渗的雨水在重力作用下从坡脚处排出,所以降雨72 h时,边坡速度矢量在边坡内部分布的面积较广,部分速度矢量箭头指向坡面。
3.4 边坡降雨入渗x方向渗流梯度分布规律由图 11可知,降雨36 h时,x方向渗流梯度等值线仅在坡脚处局部区域出现渗流梯度为负值,其余区域渗流梯度均为正值;降雨72 h时,靠近边坡内部的x方向渗流梯度等值线分布区域逐渐扩大,坡脚附近的x方向渗流梯度负值分布区域逐渐扩大,且该区域内的渗流梯度的绝对值逐渐增大。产生上述现象的原因为:边坡x方向渗流等值线以流入边坡为正,流出边坡为负。由图 10(a)可知,降雨初期雨水主要以入渗到边坡内部为主,仅有少量雨水从坡脚处排出,故仅在坡脚附近较小区域出现x方向渗流梯度为负值。由图 10(b)可知,当降雨72 h时,暂态饱和区逐渐向边坡内部扩展,渗透系数达到饱和渗透系数,雨水持续入渗到边坡内部,故靠近边坡内部x方向渗流梯度分布的区域逐渐扩大;同时,坡脚附近的暂态饱和区在重力作用下,入渗的雨水也不断从坡脚处排出,故坡脚处x方向渗流梯度负值分布区域逐渐扩大。

|
| 图 11 x方向渗流梯度 Fig. 11 Seepage gradients in x direction |
| |
3.5 导入渗流计算结果后的三维模型
将seep计算的渗流结果转化为渗透力,通过fish将基质吸力、重度修正、渗透力导入到FLAC3D中。受篇幅限制,仅给出了降雨72 h对应的基质吸力、重度、渗透力导入到FLAC3D模型中的示意图,如图 12~图 14所示。其中,考虑水位线以下浮力的影响,水位线以下粗粒土的重度采用有效重度。

|
| 图 12 导入基质吸力后的三维模型(单位:kPa) Fig. 12 Three-dimensional model after imputing matrix suction(unit:kPa) |
| |

|
| 图 13 修改密度后的三维模型(单位:kg·m-3) Fig. 13 Three-dimensional model after revising densitty (unit:kg·m-3) |
| |

|
| 图 14 导入渗透力后的三维模型 Fig. 14 Three-dimensional model after impuing seepage force |
| |
3.6 边坡降雨入渗塑性区分布规律
为真实反映降雨过程中及降雨停止后塑性区发展规律,图 15中塑性区为降雨影响新产生的塑性区,以前积累的塑性区未显示。考虑篇幅有限仅列出了降雨工况下,降雨36,72 h以及降雨停止后12,48 h的边坡塑性区发展变化分布图,如图 15所示。

|
| 图 15 高路堤塑性区分布规律 Fig. 15 Distribution of plastic zone of high embankment |
| |
由图 15可知,降雨过程中塑性区首先发生在第1级路堤边坡坡脚处并不断向第1级边坡坡脚附近延伸,当降雨历时72 h时,第2级边坡内形成较大面积的塑性贯通区;降雨停止后,塑性区的面积逐渐减小且发生在坡脚处。分析其原因为:降雨历时36 h时边坡水位线从坡脚处逐渐抬升,致使边坡坡脚处粗粒土重度增加,基质吸力减小,导致粗粒土的有效黏聚力减小;此外,边坡降雨过程中雨水首先在坡脚处汇聚,雨水汇聚过程中形成的渗透力使得边坡坡脚处易于发生塑性变形。降雨历时72 h,暂态饱和区不断向边坡内部扩展,x方向渗流梯度负值分布区域逐渐扩大,沿滑移方向的渗透力增大,即下滑力增大,故塑性区不断向边坡内部扩展。
3.7 边坡降雨入渗安全系数分布规律降雨工况下,计算得到的粗粒土高路堤边坡安全系数变化规律如图 16所示。

|
| 图 16 降雨过程中高路堤安全系数变化规律 Fig. 16 Distribution of safety factor of high embankment during rainfall |
| |
由图 16可知,降雨0~24 h内边坡安全系数先升高到1.8,降雨24~72 h内,边坡安全系数迅速下降,从1.8降到1.4;降雨停止12 h内,边坡安全系数持续降低,达到最低值1.31;降雨停止12~48 h内,边坡安全系数逐渐恢复到1.4。究其原因为:降雨0~24 h,地下水位线抬升较少,基质吸力减小较少并且此段时间内,雨水主要从坡脚处入渗到边坡内部,渗流产生的渗透力对边坡具有加固作用,所以安全系数先逐渐上升;24~72 h内,边坡坡面附近形成暂态饱和区,粗粒土渗透能力变强,雨水入渗量增大,水位线抬升速度较快,土体达到饱和,土体重度增大,边坡下滑力增大,基质吸力消散较快,导致粗粒土有效黏聚力减小并且雨水不断从坡脚处排出,渗流梯度负值分布的区域逐渐扩大,渗透力方向沿着边坡滑移方向,增大边坡下滑力,边坡塑性区向边坡内部发展,致使边坡安全系数下降的速率较快;降雨停止0~12 h后,雨水逐渐从边坡坡脚排出,渗流梯度为负值,渗透力方向沿着边坡滑移的方向,致使下滑力增大,边坡安全系数持续降低;降雨停止12~48 h后,水位线下降,基质吸力逐渐恢复,边坡安全系数逐渐恢复。
4 结论(1) 随降雨历时的增加,粗粒土高路堤边坡水位线逐渐抬升,靠近边坡坡面的水位线抬升的速率明显快于道路中心线附近的水位线抬升速率;降雨停止后,水位线逐渐下降。
(2) 降雨过程中随着水位线的抬升,粗粒土高路堤边坡基质吸力逐渐消散并逐渐转变为正孔隙水压力,降雨停止后基质吸力逐渐恢复。
(3) 随降雨历时增加,粗粒土高路堤边坡x方向渗流梯度在坡脚处逐渐出现负值且负值区域逐渐扩大,因此考虑渗透力来计算边坡稳定性,能更真实地反映雨水入渗过程中边坡稳定性的变化规律。
(4) 初始条件下粗粒土高路堤边坡塑性区主要发生在坡脚处,随降雨历时的增加,边坡塑性区逐渐向边坡内部发展;边坡安全系数先升高后逐渐降低;降雨停止后边坡塑性区主要发生在坡脚处,安全系数逐渐恢复,但有一定滞后性。
| [1] | JTG D30-2015, 公路路基设计规范[S]. JTG D30-2015, Specifications for Design of Highway Subgrades[S]. |
| [2] | 陈晓斌, 徐望国, 刘小平. 降雨入渗对粗粒土路堤变形与稳定性的影响[J]. 中南大学学报:自然科学版, 2011, 42(3): 765-771 CHEN Xiao-bin, XU Wang-guo, LIU Xiao-ping. Effect of Rainfall Infiltration on Additional Settlement and Stability Debasement of Granular Soil Fillings Embankment[J]. Journal of Central South University:Natural Science Edition, 2011, 42(3): 765-771 |
| [3] | 李广信. 论土骨架与渗透力[J]. 岩土工程学报, 2016, 38(8): 1522-1528 LI Guang-xin. On Soil Skeleton and Seepage Force[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(8): 1522-1528 |
| [4] | 陈祖煜. 土质边坡稳定性分析[M]. 北京: 中国水利水电出版社, 2003. CHEN Zu-yu. Stability Analysis of Soil Slopes[M]. Beijing: China Water & Power Press, 2003. |
| [5] | 连继峰, 罗强, 蒋良潍, 等. 顺坡渗流条件下土质边坡浅层稳定分析[J]. 岩土工程学报, 2015, 37(8): 1440-1448 LIAN Ji-feng, LUO Qiang, JIANG Liang-wei, et al. Shallow Stability Analysis of Soil Slopes under Seepage Parallel to Slope Surface[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1440-1448 |
| [6] | 刘子振, 言志信. 降雨入渗非饱和黏土边坡稳定性的极限平衡条分法研究[J]. 岩土力学, 2016, 37(2): 350-356 LIU Zi-zhen, YAN Zhi-xin. Limit Equilibrium Slice Method for Unsaturated Clay Slope under Rainfall Infiltration[J]. Rock and Soil Mechanics, 2016, 37(2): 350-356 |
| [7] | 汪丁建, 唐辉明, 李长冬, 等. 强降雨作用下堆积层滑坡稳定性分析[J]. 岩土力学, 2016, 37(2): 439-445 WANG Ding-jian, TANG Hui-ming, LI Chang-dong, et al. Stability Analysis of Colluvial Landslide due to Heavy Rainfall[J]. Rock and Soil Mechanics, 2016, 37(2): 439-445 |
| [8] | 付宏渊, 邱祥, 李光裕, 等. 降雨入渗条件下炭质泥岩路堤动态稳定性[J]. 长安大学学报:自然科学版, 2017, 37(1): 33-42 FU Hong-yuan, QIU Xiang, LI Guang-yu, et al. Dynamic Stability of Carbonaceous Mudstone Embankment under Rainfall Infiltration[J]. Journal of Chang'an University:Natural Science Edition, 2017, 37(1): 33-42 |
| [9] | 宋子亨, 杨强, 刘耀儒. 考虑孔隙水压力作用的岩土体弹塑性模型及其有限元实现[J]. 岩土力学, 2016, 37: 500-508 SONG Zi-heng, YANG Qiang, LIU Yao-ru. Elastoplastic Model for Geomaterial Considering Effect of Pore Water Pressure and Its Finite Elements Implementation[J]. Rock and Soil Mechanics, 2016, 37(S1): 500-508 |
| [10] | 马年祖, 建德琳, 代玉莉, 等. 山岭重丘区道路改扩建路基持续降雨渗流数值模拟[J]. 公路交通科技, 2016, 33(9): 31-37, 45 MA Nian-zu, JIAN De-lin, DAI Yu-li, et al. Numerical Simulation of Subgrade Persistent Rainfall Seepage of Reconstructed Highway in Mountainous and Heavy-hilly Area[J]. Journal of Highway and Transportation Research and Development, 2016, 33(9): 31-37, 45 |
| [11] | 付宏渊, 曾铃, 王桂尧. 降雨入渗条件下软岩边坡稳定性分析[J]. 岩土力学, 2012, 33(8): 2359-2365 FU Hong-yuan, ZENG Ling, WANG Gui-yao. Stability Analysis of Soft Rock Slope under Rainfall Infiltration[J]. Rock and Soil Mechanics, 2012, 33(8): 2359-2365 |
| [12] | 杨金, 简文星, 杨虎锋, 等. 三峡库区黄土坡滑坡浸润线动态变化规律研究[J]. 岩土力学, 2012, 33(3): 853-858 YANG Jin, JIAN Wen-xing, YANG Hu-feng, et al. Dynamic Variation Rule of Phreatic Line in Huangtupo Landslide in Three Gorges Reservoir Area[J]. Rock and Soil Mechanics, 2012, 33(3): 853-858 |
| [13] | 魏义长, 刘作新, 康玲玲, 等. 土壤持水曲线van Genuchten模型求参的Matlab实现[J]. 土壤学报, 2004, 41(3): 380-386 WEI Yi-chang, LIU Zuo-xin, KANG Ling-ling, et al. Parameters Estimation of Van Genuchten Model for Soil Water Retention Curves Using Matlab[J]. ACTA Pedologica Sinica, 2004, 41(3): 380-386 |
| [14] | 蒋中明, 龙芳, 熊小虎, 等. 边坡稳定性分析中的渗透力计算方法考证[J]. 岩土力学, 2015, 36(9): 2478-2486, 2493 JIANG Zhong-ming, LONG Fang, XIONG Xiao-hu, et al. Study of Calculation Methods of Acting Force of Seepage in Slope Stability Analysis[J]. Rock and Soil Mechanics, 2015, 36(9): 2478-2486, 2493 |
| [15] | 顾慰慈. 渗流计算原理及应用[M]. 北京: 中国建材工业出版社, 2000. GU Wei-ci. The Principle and Application of Seepage Calculation[M]. Beijing: China Building Materials Industry Press, 2000. |
| [16] | FREDLUND D G, MORGENSTERN N R, WIDGER R A. The Shear Strength of Unsaturated Soils[J]. Canadian Geotechnical Journal, 1978, 15(3): 313-321 |
| [17] | 宋焕宇. 粗粒土斜坡高路堤变形性状与稳定性研究[D]. 武汉: 华中科技大学, 2007. SONG Huan-yu. Study on Deformation Characteristics and Stability of High Embankment Filled by Coarse Grained Soils on Sloping Ground[D]. Wuhan:Huazhong University of Science and Technology, 2007. http://cdmd.cnki.com.cn/article/cdmd-10487-2009033682.htm |
| [18] | 曾铃, 付宏渊, 何忠明, 等. 饱和-非饱和渗流条件下降雨对粗粒土路堤边坡稳定性的影响[J]. 中南大学学报:自然科学版, 2014, 45(10): 3614-3620 ZENG Ling, FU Hong-yuan, HE Zhong-ming, et al. Impact of Rainfall on Stability of Granular Soil Embankment Slope Considering Saturated-unsaturated Seepage[J]. Journal of Central South University:Science and Technology Edition, 2014, 45(10): 3614-3620 |
 2017, Vol. 34
2017, Vol. 34
