扩展功能
文章信息
- 何丽丽, 郭庆林, 周小利, 原冬霞
- HE Li-li, GUO Qing-lin, ZHOU Xiao-li, YUAN Dong-xia
- 悬臂梁结构振动系统的鲁棒主动控制优化
- Robust Active Vibration Control Optimization of Cantilever Beam Structure
- 公路交通科技, 2017, 34(8): 145-151
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(8): 145-151
- 10.3969/j.issn.1002-0268.2017.08.020
-
文章历史
- 收稿日期: 2017-01-04
在航空航天领域和机械领域中,许多柔性机构或构件诸如飞机的壁板和机翼、太阳能帆板、大型精密天线、车辆悬架等,具有尺寸大、柔性高的特点,很容易受到气流、宇宙风、微粒子流、不平整路面等各种外力的扰动产生振动,而且结构振动自由衰减的速度很慢,对整个系统的安全性能,控制系统的可靠性和灵活性以及噪声污染方面有更高的要求,因此,各种振动主动控制方法已成为国内外学者研究的热点课题[1]。文献[2]针对车辆悬架为一非线性、时滞、不确定系统,设计了一种改进的主动悬架模糊PID控制器。在研究1/2车辆模糊控制半主动悬架的基础上,考虑发动机和人椅系统等因素,文献[3]建立了车椅人1/4车体4自由度车辆动力学模型,设计了自适应模糊PID控制器,结果表明,模糊PID控制器使车辆行驶的平顺性更好。近年来,将压电智能材料作为传感器/驱动器设计控制器为柔性结构的振动主动控制开辟了一条新的有效途径,压电智能材料以其优良的机电耦合特性被越来越多地应用于航空航天、机械结构的振动主动控制当中[4],文献[5]以压电柔性结构为研究对象,考虑了被控模态参数的不确定性,建立了结构的不确定线性分式模型,设计了一个对结构进行振动主动控制的动态输出反馈控制器。然而,基于模型降阶的控制器由于忽略了高频未建模动态的影响,有可能产生“溢出”问题从而导致闭环系统不稳定。因此,考虑高频未建模动态等不确定性问题影响的鲁棒控制方法受到很多专家学者的重视[6-8],传统的鲁棒控制方法得到的控制器性能在很大程度上取决于模型的准确程度[9-11],柔性结构由于模型阶次较高,文献[12]考虑了模态频率摄动对控制性能的影响, 提出了对模态参数摄动具有鲁棒性的独立模态鲁棒H∞控制;文献[13]基于ANSYS/APDL参数化语言编制了能够准确描述层合压电智能结构力-电耦合场的有限元数值模型,通过有限元数值模拟,研究了悬臂板自由端在瞬时荷载和简谐荷载作用下振动控制问题;文献[14]考虑了由于模型降阶引起的模型误差, 设计了一个鲁棒H∞控制器,然而其降阶模型的获得均是通过试验得到的,增加了很多人为因素和试验环境的影响,同时大大增加了控制成本投入。
文中基于ANSYS软件数值模拟得到了压电柔性悬臂梁结构的模态振型,与常用的柔性结构试验建模方法不同,有限元分析方法更为直接,避免了试验建模的繁琐性、复杂性及较高的成本投入。通过与理论结果相比较,说明其分析结果的正确性。然后,基于此模型,通过分析系统存在的模型不确定性以及选取适当的权函数,最终完成了柔性悬臂梁结构振动系统的鲁棒控制器设计。仿真结果表明,基于H∞控制理论的混合灵敏度分析方法的鲁棒控制器能有效抑制悬臂梁的振动,振动系统的动态性能及鲁棒性能均得到了极大改善。
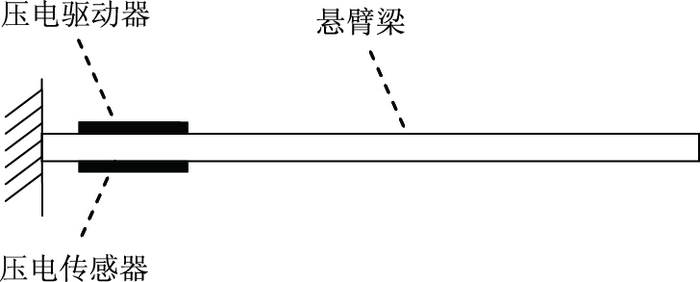
1 控制系统模型文中采用压电传感器和驱动器对称布置的原则,保证了控制系统的最小相位,能够避免由于模态截断导致的观测和控制的溢出,压电柔性悬臂梁的物理模型如图 1所示[15]。
|
| 图 1 压电柔性悬臂梁物理模型简图 Fig. 1 Schematic diagram of physical model of piezoelectric flexible cantilever beam |
| |
应用ANSYS软件建模并进行数值计算,其中,柔性悬臂梁采用SOLID45三维单元进行模拟,压电传感器和驱动器采用SOLID5三维单元进行模拟,有限元模型的边界条件为:一端为固定端约束,限制所有方位移动和转动作用,另一端自由。悬臂梁和压电元件各自的材料性质如表 1和表 2所示。
| 悬臂梁材料 | 密度/(kg·m-3) | 泊松比 | 弹性模量/(N·m-2) |
| SOLID45 | 2 743 | 0.270 0 | 7.5842×1010 |
| PZT-5H | 密度/
(kg·m-3) | 柔度系数/(×1010 N·m-2) | 相对介电常数 | 压电应力常数/(c·m-2) | ||||||||
| c11 | c12 | c13 | c33 | c44 | c66 | ε11S/ε0 | ε33S/ε0 | e33 | e31 | e15 | ||
| SOLID5 | 7 700 | 12.60 | 7.95 | 8.41 | 11.70 | 23 | 23.30 | 1 697.53 | 1 468.26 | 23.30 | -6.50 | 17 |
通过ANSYS软件模态分析,压电柔性悬臂梁结构的前3阶模态频率分别为:f1=2.977 5 Hz,f2=18.681 0 Hz,f3=52.580 0 Hz。用结构动力学瑞利法[16]计算得到的解析结果分别为:f1=2.971 2 Hz,f2=18.509 1 Hz,f3=52.091 0 Hz,解析结果与ANSYS软件分析结果比较,误差分别为:0.21%,0.92%,0.93%。可见,此结果与理论计算结果误差较低。压电柔性悬臂梁结构的前3阶模态振型如图 2所示。

|
| 图 2 柔性结构前3阶模态振型 Fig. 2 First 3 order mode shapes of flexible structure |
| |
2 H∞鲁棒控制 2.1 标准H∞控制器设计
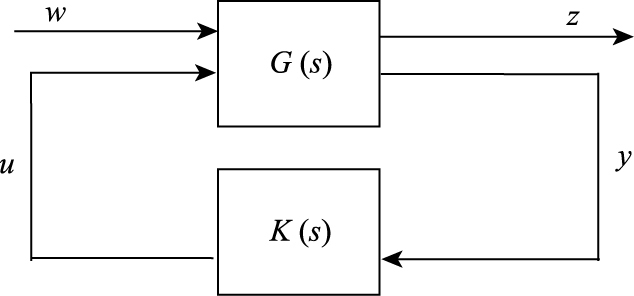
标准H∞控制器设计问题如图 3所示,其中,w∈Rp为外部输入信号,包括噪声、参考输入、干扰等,z∈Rm为被控输出信号,u∈Rr为控制信号,y∈Rq为4测量信号,G(s)为广义被控对象,包括实际对象和加权函数,K(s)为所设计的控制器[8]。
|
| 图 3 标准H∞控制问题 Fig. 3 Normal H∞ control problem |
| |
输入输出描述为:
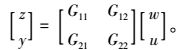
|
(1) |
输入输出对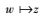
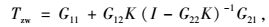
|
(2) |
则标准H∞控制问题就可以表述为:求取一正则控制器K,使闭环传递函数Tzw的H∞范数达到极小,即[17]:
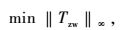
|
(3) |
式(3) 为H∞最优控制问题。若给定γ>0,求取镇定控制器K,使
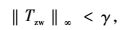
|
(4) |
则为H∞次优控制问题。
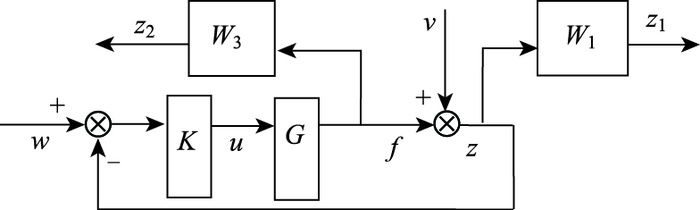
2.2 H∞混合灵敏度问题考虑如图 4所示的混合灵敏度优化问题,w为参考输入,v为扰动,z为系统输出,K为控制器,G为被控对象。对于这个系统,灵敏度函数S以及补灵敏度函数T分别定义为:
|
| 图 4 混合灵敏度优化问题 Fig. 4 Mixed sensitivity optimization problem |
| |
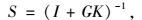
|
(5) |
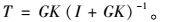
|
(6) |
灵敏度函数S(jω)的奇异值决定了扰动衰减特性,因为S(jω)实际上是扰动v到对象输出z的闭环传递函数。扰动衰减性能要求可以表述成:
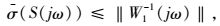
|
(7) |
式中,|W1-1(jω)|为期望扰动衰减因子,W1(jω)为鲁棒性能权函数。σ(S(jω))越小,反馈控制系统对外干扰信号的抵抗能力就愈强。
补灵敏度函数T(jω)的奇异值决定了系统中乘性摄动Δm的稳定裕量。假设系统存在如图 5所示的乘性摄动Δm(jω),并且用Δm(jω)的奇异值来定义Δm(jω)的大小,根据小增益定理,假设如图 5所示的系统,其中乘性摄动Δm是稳定的,并且Δm≠0,那么当这个系统变成不稳定时,最小的稳定Δm为:

|
| 图 5 系统中的乘性摄动 Fig. 5 Multiplicative perturbation of system |
| |
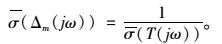
|
(8) |
从这个定理可以看出,σ(T(jω))越小,最小的引起系统不稳定的乘性摄动Δm越大,因此系统的稳定裕量也就越大。
同样地,可以通过奇异值不等式定义系统的稳定裕量为:
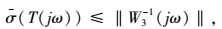
|
(9) |
式中W3(jω)为鲁棒稳定性权函数。
在选择权函数W1和W3时,需要注意的一点是,在Bode图中W1与0 dB线的交界频率必须充分地低于W3与0 dB线的交界频率。更确切地说,在设计考虑的频段内,选择的权函数必须满足:
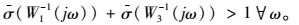
|
(10) |
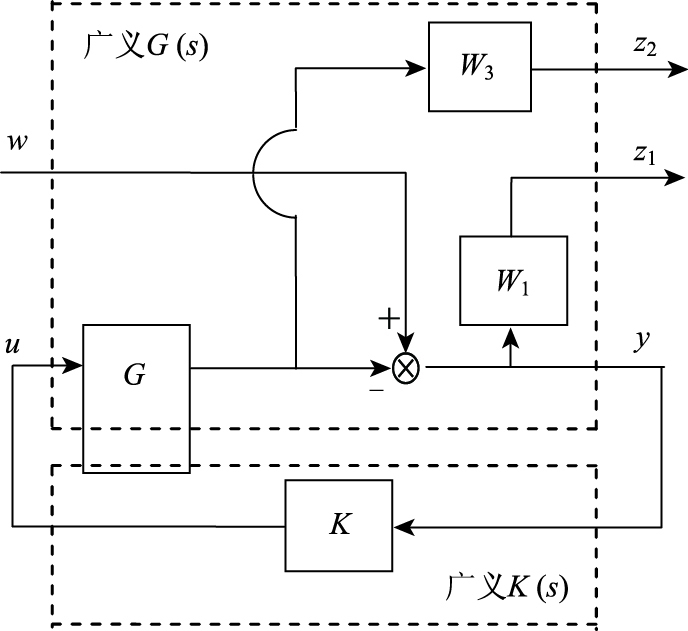
由于S+T=I,因此,在设计系统时,综合考虑灵敏度函数S和补灵敏度函数T,才能达到整体鲁棒稳定性的目的,由图 4可知,w到期望输出z1和z2的传递函数分别为W1S和W3T,把混合灵敏度优化问题转化为H∞标准问题模型如图 6所示[18]。
|
| 图 6 混合灵敏度优化的等价标准问题 Fig. 6 Equivalence standard problem of mixed sensitivity optimization |
| |
此时,输入输出对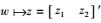
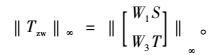
|
(11) |
由式(7) 和式(9) 可知,混合灵敏度方法实际上就转化成了H∞次优控制问题,即求取镇定控制器K,满足:
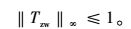
|
(12) |
也就是说,通过选择合适的W1和W3权函数,然后极小化闭环传递函数Tzw的H∞范数,求出鲁棒反馈控制器,使闭环系统的鲁棒性能达到期望指标。
2.3 鲁棒控制律的设计已有的研究表明[15],结构前3阶模态自由衰减很慢,故文中考虑前3阶的振动抑制问题。梁的截面宽乘高为0.025 4 m×0.000 8 m,梁的跨度为0.504 0 m,压电元件的宽乘高为0.025 4 m×0.000 2 m,跨度为0.025 4 m。压电元件布置在距离悬臂端0.132 0 m处。
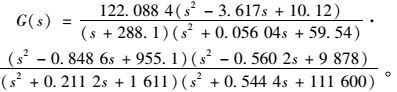
|
(13) |
基于以上ANSYS分析结果,为了描述柔性梁的前3阶模态,传递函数至少采用六阶模型,同时,考虑到剩余模态及外部扰动的影响,传递函数模型式(13) 取为七阶。
合适的权函数W1和W3的选择,很大程度上决定了H∞混合灵敏度设计方法的成功[18],因为W1和W3是代表期望设计指标的频域权函数,在低频到中频段极小化S有利于提高跟踪能力和扰动衰减能力。而由于传感器/驱动器噪声,未建模高阶动力学特性影响以及对象参数变化的存在,为了提高鲁棒稳定性则需要在高频段极小化T。
因此,文中经过筛选和经验选取了如下的鲁棒性能权函数和鲁棒稳定性权函数:
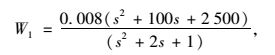
|
(14) |
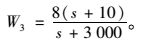
|
(15) |
W1和W3的幅频/相频图见图 7,从图中可以看出,鲁棒稳定性权函数W3(jω)的0 dB交界频率远大于柔性悬臂梁的3阶共振频率52.580 0 Hz,且在所有频率范围内权函数W3(jω)的幅值是递增的。

|
| 图 7 加权函数波德(幅频/相频)图 Fig. 7 Bode (magnitude/amplitude) diagram of weighting function |
| |
3 控制仿真
柔性结构本质上是一个无穷维分布参数系统,由于只考虑了前3阶振动模态,其余被忽略的高阶剩余模态构成了系统的不确定性,有可能导致基于降阶模型设计的控制器并不能真正适用于实际系统,这种基于H∞理论的混合灵敏度方法设计的鲁棒控制器,能够很好地消除溢出现象。
考虑从式(16) 得到的乘性摄动:
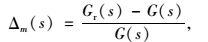
|
(16) |
式中,Gr(s)为实际被控对象;G(s)为名义被控对象。根据鲁棒控制的观点,在模型不确定性存在的情况下,权函数W3(jω)应该设计成在任意频率点均大于乘性摄动Δm(s),即:
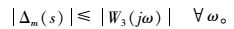
|
(17) |
一般而言,W3(jω)可以大致认为是频率ω的增函数,因此不确定性可随着频率的增加而增加。从图 7中可以看出文中设计的W3(jω)满足上述要求,故从理论上讲,文中所设计的控制器在上述不确定性存在的条件下,仍然能够维持闭环系统的稳定性。
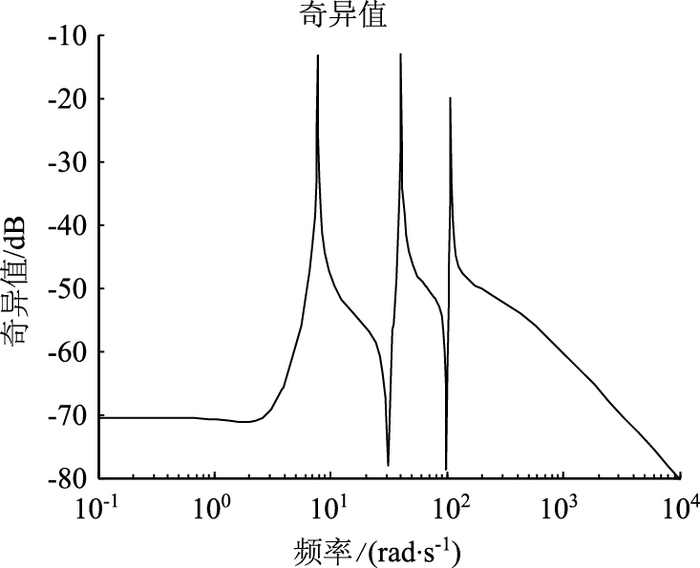
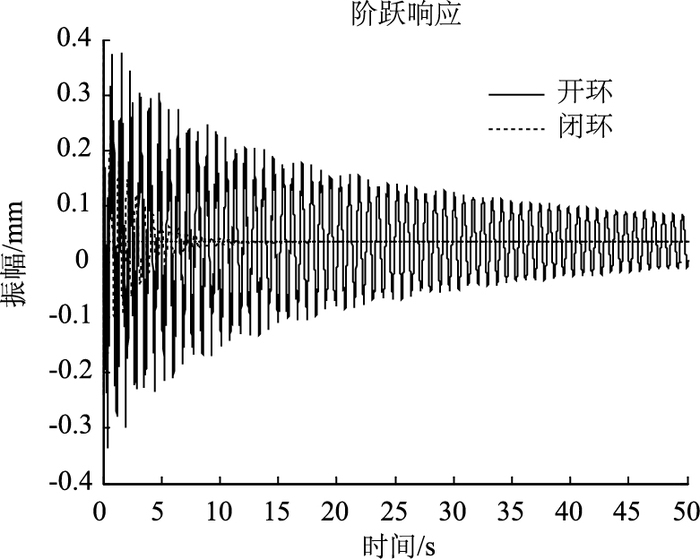
文中对此振动系统进行了控制仿真,从频率域上进行分析,其闭环传递函数的奇异值曲线见图 8。图 8表明,奇异值均在0 dB以下,这就证明式(12) 的不等式约束得到了满足, 同时表明文中选择的权函数有较强的抑制外扰能力。从时域上进行分析,振动系统的单位阶跃响应曲线见图 9。通过比较系统的开环和闭环响应可以看出,在H∞鲁棒控制器的作用下,闭环振动系统在10 s左右就衰减到最大幅值的5%以内,并且最终趋于稳定,同时,闭环系统在振幅趋于0之后相当长的时间里并没有出现溢出不稳定现象。这证明闭环系统的鲁棒性能也得到了很大的改善。
|
| 图 8 闭环传递函数奇异值 Fig. 8 Singular values of closed-loop transfer function |
| |
|
| 图 9 系统阶跃响应曲线 Fig. 9 Step response curve of system |
| |
4 结论
文中研究了柔性悬臂梁结构振动系统的鲁棒主动控制策略,基于ANSYS软件数值模拟得到压电柔性悬臂梁结构的模态振型。基于此模型,通过分析系统存在的模型不确定性以及选取适当的权函数,最终完成了柔性悬臂梁结构振动系统的鲁棒控制器设计。仿真结果表明,基于H∞控制理论的混合灵敏度分析方法的鲁棒控制器能有效抑制悬臂梁的振动,振动系统的动态性能及鲁棒性能均得到了极大改善。
| [1] | 马天兵. 压电智能结构振动主动控制关键技术研究[D]. 南京: 南京航空航天大学, 2014. MA Tian-bing. Research on Key Technologies of Active Vibration Control for Piezoelectric Smart Structures[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10287-1015951832.htm |
| [2] | 陈翔, 宋庆阳, 刘新成. 改进的模糊PID控制器对4自由度主动悬架振动控制的研究[J]. 公路交通科技, 2009, 26(2): 129-133 CHEN Xiang, SONG Qing-yang, LIU Xin-cheng. Research on Vibrating Control of 4-DOF Active Suspension with Improved Fuzzy PID Controller[J]. Journal of Highway and Transportation Research and Development, 2009, 26(2): 129-133 |
| [3] | 陈翔, 白月飞, 张林燕, 等. 考虑发动机与人椅系统的液压半主动悬架振动控制研究[J]. 公路交通科技, 2011, 28(1): 127-131, 137 CHEN Xiang, BAI Yue-fei, ZHANG Lin-yan, et al. Research on Vibrating Control of Hydraulic Semi-active Suspension Considering Engine and Passenger-seat System[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1): 127-131, 137 |
| [4] | 李生权, 季宏丽, 裘进浩. 基于压电智能结构状态估计误差补偿的自抗扰振动控制[J]. 机械工程学报, 2012, 48(5): 34-42 LI Sheng-quan, JI Hong-li, QIU Jin-hao. Active Disturbance Rejection Controller Based on State Estimation Error Compensation for Smart Piezoelectric Structure[J]. Journal of Mechanical Engineering, 2012, 48(5): 34-42 |
| [5] | 徐亚兰, 陈建军, 王小兵. 模型不确定压电柔性结构的多目标振动控制[J]. 应用力学, 2006, 23(3): 377-382, 508 XU Ya-lan, CHEN Jian-jun, WANG Xiao-bing. Multiobjective Vibration Control for Uncertain Flexible Structures[J]. Chinese Journal of Applied Mechanics, 2006, 23(3): 377-382, 508 |
| [6] | 徐亚兰, 陈建军, 王小兵. 模型不确定压电柔性结构的鲁棒振动控制[J]. 机械强度, 2006, 28(2): 185-189 XU Ya-lan, CHEN Jian-jun, WANG Xiao-bing. Robust Vibration Control for Uncertain Flexible Structures[J]. Journal of Mechanical Strength, 2006, 28(2): 185-189 |
| [7] | 周克敏, DOYLEJ C, GLOVERK. 鲁棒与最优控制[M]. 北京: 国防工业出版社, 2002. ZHOU Ke-min, DOYLE J C, GLOVER K. Robust and Optimal Control[M]. Beijing: National Defense Industry Press, 2002. |
| [8] | 彭程, 王永. 柔性梁降阶H∞控制实验研究[J]. 振动与冲击, 2007, 26(10) 64-67, 188-189 PENG Cheng, WANG Yong. An Experimental Study on Reduced Order H∞ Control of a Flexible Beam[J]. Journal of Vibration and Shock, 2007, 26(10) 64-67, 188-189 |
| [9] | MOREIRA F J O. DE FRANÇA ARRUDA J R, INMAN D J. Design of a Reduced Order H∞ Controller for Smart Structure Satellite Applications[[J]. Philosophical Transactions:Mathematical, Physical and Engineering Sciences, 2001, 359(1788): 2251-2269 |
| [10] | 赖胜, 王永, 孙德敏. 基于频域辨识模型的柔性板鲁棒振动主动控制[J]. 系统仿真学报, 2005, 17(4): 957-961 LAI Sheng, WANG Yong, SUN De-min. Robust Active Vibration Control for a Flexible Plate Based on Frequency Domain Identified Model[J]. Journal of System Simulation, 2005, 17(4): 957-961 |
| [11] | 胡如夫, 李普, 陈南, 等. 基于H∞的振动系统多输入多输出鲁棒控制仿真[J]. 东南大学学报:自然科学版, 2005, 35(6): 894-897 HU Ru-fu, LI Pu, CHEN Nan, et al. MIMO Robust Control Simulation for Vibration System Based on H∞ Scheme[J]. Journal of Southeast University:Natural Science Edition, 2005, 35(6): 894-897 |
| [12] | 林嗣廉, 徐博侯. 柔性结构振动的独立模态H∞控制[J]. 浙江大学学报:工学版, 2001, 35(1): 23-29 LIN Si-lian, XU Bo-hou. Independent Modal H∞ Control of Vibration Flexible Structures[J]. Journal of Zhejiang University:Engineering Science Edition, 2001, 35(1): 23-29 |
| [13] | 钱锋. 层合压电智能结构振动主动控制数值模拟及其优化[D]. 合肥: 合肥工业大学, 2011. QIAN Feng. Numerical Modelling and Optimization of Laminated Piezoelectric Smart Structure Active Vibration Control[D]. Hefei:Hefei University of Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10359-1011124241.htm |
| [14] | SANA S, RAO V S. Application of Linear Matrix Inequalities in the Control of Smart Structural Systems[J]. Journal of Intelligent Material System & Structures, 2000, 11(4): 311-323 |
| [15] | 张京军, 何丽丽, 王二成, 等. 压电智能结构振动主动控制传感器/驱动器的位置优化设计[J]. 工程力学, 2010, 27(1): 228-239 ZHANG Jing-jun, HE Li-li, WANG Er-cheng, et al. The Optimal Position Design of Sensors/Actuators in Active Vibration Control for Piezoelectric Intelligent Structures[J]. Engineering Mechanics, 2010, 27(1): 228-239 |
| [16] | 刘晶波, 杜修力. 结构动力学[M]. 北京: 机械工业出版社, 2005. LIU Jing-bo, DU Xiu-li. Structural Dynamics[M]. Beijing: China Machine Press, 2005. |
| [17] | 李蒙, 石泳, 刘莉. 基于鲁棒H∞的无人机飞行控制系统设计及实现[J]. 北京理工大学学报, 2016, 36(8): 807-812 LI Meng, SHI Yong, LIU Li. Development of UAV Autopilot Based on Robust H∞ Theory[J]. Transactions of Beijing Institute of Technology, 2016, 36(8): 807-812 |
| [18] | 李航. 基于漂浮式平台的海上风力发电机组变桨控制研究[D]. 沈阳: 沈阳工业大学, 2014. LI Hang. Pitch Control Study of Offshore Floating Wind Turbine[D]. Shenyang:Shenyang University of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10142-1014304688.htm |
 2017, Vol. 34
2017, Vol. 34
