扩展功能
文章信息
- 潘兵宏, 霍永富, 刘斌, 周海宇, 武生权
- PAN Bing-hong, HUO Yong-fu, LIU Bin, ZHOU Hai-yu, WU Sheng-quan
- 基于UCWin/Road仿真的高速公路出口预告标志前置距离研究
- Study on Advance Distance of Expressway Exit Guide Sign Based on UCWin/Road Simulation
- 公路交通科技, 2017, 34(8): 130-137
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(8): 130-137
- 10.3969/j.issn.1002-0268.2017.08.018
-
文章历史
- 收稿日期: 2016-10-24
2. 长安大学 特殊地区公路工程教育部重点实验室, 陕西 西安 710064
2. Key Laboratory for Special Area Highway Engineering of Ministry of Education, Xi'an Shaanxi 710064, China
随着国家基础建设的逐步推进,全国高速公路网也趋于完善。交通运输部数据显示,截止到2015年末,全国高速公路里程达到12.35万km。虽然路网得到不断完善,路网节点也更加密集,但高速公路互通式立交出口依然是交通事故高发地。国内外的事故统计表明,超过30%的高速公路事故发生于高速公路出入口及附近[1],其中出口的事故率更高,驾驶人因错过出口,采取倒车或强行变道驶出而导致的恶性事故也时有发生。这其中一个主要原因是高速公路出口前置预告指路标志(Advance Guide Sign,AGS)距离设置不合理,驾驶人不能从容变道驶出,从而导致事故。《交通工程手册》[2](以下简称《交通手册》)和《道路交通标志和标线》(GB 5768—2009)[3](以下简称《标志标线》)均规定高速公路出口预告标志分别设置在距减速车道渐变段起点2 km,1 km,500 m的地点和减速车道起点,这个距离与高速公路的设计速度和车道数无关,可能存在不合理之处。如何科学合理地设置高速公路出口标志的前置距离,特别是最后一块出口距离预告标志的位置,成为了出口标志设置亟待解决的问题之一。
目前对AGS距离的研究较多, SONG等[4]提出了基于平均速度曲线偏差率算法的标志设置距离方法,但该方法存在工作量大、不易实现的缺点。郭唐仪等[5]建立了AGS设置距离模型,但其模型中AGS基准点有误,且减速车道上的减速距离模型没有考虑匝道设计速度和驾驶行为,导致AGS计算距离过短。刘伟铭等[6]建立了基于车道变换模型的AGS设置模型,但其模型中车头时距采用M3模型,而高速公路互通式立交驶出段并不适用该模型。崔洪军等[7]建立了基于变道成功率的车辆间隔距离模型,但其模型中换道距离仅考虑了车辆转向角度,没有考虑车辆运行连续性及舒适性。
本研究从驾驶心理学原理和驾驶人对标志的响应特性出发,将准备驶出的驾驶人驾驶操作行为进行分段分析,并结合驶出驾驶人对标志的认读特点,考虑驾驶人的横向位置及变道特点,建立合理的AGS设置距离模型,并分析基于不同设计速度和车道数的AGS的合理设置距离。
1 计算模型分析《交通手册》中司机将标志的视认过程分为发现、判别、认读、理解、采取行动5个阶段。李爱增等[8]以交通心理学为基础,将驾驶人看到标志后的行为分为发现标志、读取标志、进行决策、实施操作4个阶段。本文从驾驶心理学原理和驾驶人对标志的响应特性出发,以驾驶人对交通标志所传递信息接收和处理的基本顺序为依据,将驾驶人行为过程分为5段,即:发现段、读取段、决策段、行动段、确认段(图 1)。

|
| 图 1 驾驶人行为过程 Fig. 1 Driver's behavior process |
| |
以双向四车道为例,最不利的情况是行驶中处于最内侧车道的车辆在A点处发现标志牌,到B点看清标志牌后开始读取标志牌信息,到C点读取完毕,B到C段距离为读取距离dr。根据标志牌信息判断应该采取变道驶出的行动,到D点开始采取行动,C到D段距离为决策距离dd。从D点开始驾驶人等待右侧车道车流出现可插入间隙,到E点找到可插入间隙并开始准备换道,D到E段距离为等待可插入间隙行驶距离dw。从E点开始换道,到F点变换到右侧车道,E到F段距离为换道行驶距离dh。F到G段距离为确认出口距离dc。图 1中B到K为视认距离L,K到G为AGS距离D,驾驶人至少在出口标志消失前应满足驾驶完成标志信息读取的距离,消失段距离为S,所以AGS距离D的计算模型如式(1) 所示:

|
(1) |
读取距离dr是指驾驶人看到出口标志牌后,开始读取信息,直到读取完成期间车辆行驶的距离。决策距离dd是指驾驶人读完出口相关信息后,思考如何采取措施行动期间车辆行驶的距离。在以上车辆行驶距离中,驾驶人注意力集中在标志牌上,对车辆一般不会采取减速或加速的措施,并且时间较短,所以可近似认为车辆处于匀速行驶状态,则读取距离dr和决策距离dd可以分别用式(2) 和式(3) 计算:

|
(2) |

|
(3) |
式中,vd为高速公路设计速度;tr为读取标志所需要的时间,一般取1~2 s[9],本文取2 s;td为决策需要思考的时间,一般取2~2.5 s[9],本文取2 s。
2.2 等待可插入间隙行驶距离有很多研究认为立交出口分流段车头时距服从M3分布[7],试验及理论均表明M3适用于拥挤流,如交通拥堵的城市道路,但对高速公路立交出口段并不适用。相关研究表明,在立交合流区200 m以外的车头时距服从三阶爱尔朗分布[10],而立交合流影响区和立交分流影响区较相似。大量研究表明[3],分流区紊流程度随距分流点距离的增加而减弱,稳流严重的区段从分流点到上游450 m,紊流的影响区段则可至上游1 000 m处。《公路工程技术标准》(JTG B01—2014)(以下简称《标准》)[11]规定,立交出口采用三级服务水平,此时交通流处于稳定流,而K阶爱尔朗分布适于自由流与拥挤流之间的稳定流描述,所以本文采用三阶爱尔朗车头时距模型。
在高速公路上,车辆到达服从泊松分布,交通流为稳定流时,车头时距服从K阶爱尔朗分布,当其用于单车道交通流时,理论上会得出大量的0~1.2 s的车头时距[12],但实际上不会出现这样的情况。因为车头时距应大于车身长度加一定安全距离。将三阶爱尔朗分布曲线从原点沿t轴右移τ(最小间隔长度),便得到了移位三阶爱尔朗分布曲线,在三级服务水平下,高速公路出口匝道分流区附近(大于200 m)符合移位三阶爱尔朗分布,由交通流理论可建立等待可插入间隙行驶距离模型。
K阶爱尔朗分布概率为:

|
(4) |
式中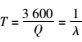
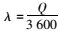
概率密度函数为:

|
(5) |
移位三阶爱尔朗分布车头时距大于等于t的概率为:

|
(6) |
式中, h为车头时距;t为时间;i取0, 1, 2;τ为目标车道上车辆车头时距的最小值,一般取1.5 s。
相应的概率密度为:

|
(7) |
可求任意一个被拒绝的间隔,其分布为:

|
(8) |
式中tc为车辆临界间隙,一般取3.5 s。
所以被拒绝的间隔平均长度h为:

|
(9) |
车辆拒绝m个不可接受间隙的概率为:

|
(10) |
拒绝间隔的平均个数n为:

|
(11) |
平均等待时间tw为:

|
(12) |
计算得到等待可插入间隙平均时间及距离如表 1所示。
| 主线运行速度/(km·h-1) | 120 | 100 | 80 |
| 每车道最大服务交通量/(pcu·h-1) 单位时间平均到达率/(pcu·s-1) | 1 650 0.458 | 1 600 0.444 | 1 500 0.417 |
| 等待可插入间隙平均时间/s 等待可插入间隙行驶距离/m | 7.864 262 | 7.276 202 | 6.243 139 |
2.3 换道行驶距离
车辆在高速公路出口段会有多次换道行为。笔者查阅大量文献,发现目前国内外常用的换道模型有以下几种:等速偏移模型、圆直模型、缓和曲线模型、正弦曲线模型、双曲正切曲线模型及多项式回归曲线模型等[13-14]。根据杨建国等[15]的研究成果可知,实际换道过程中应满足两条基本原则:第一,换道过程中,行车轨迹的曲率应连续变化,不会发生突变;第二,换道轨迹起终点的曲率最小为零。但上述模型均存在起终点曲率不为零或行车轨迹曲率突变,实际行车中不可能出现这些情况,因此上述模型均存在不足,不宜直接使用。
针对上述模型的不足,等速偏移换道模型和正弦曲线换道模型曲线上各个点的曲率连续变化,无曲率突变点;起终点曲率为零, 综合其优点,提出采用等速偏移正弦曲线换道模型[13],其表达式为:

|
(13) |
式中,W为两相邻行车道中线的距离;dh为换道所需纵向行驶距离;x为t时刻车辆行驶的距离,x=vt,式中由于t较小,所以v取主线设计速度。
将式(13) 对时间t求导,得到:

|
(14) |

|
(15) |

|
(16) |
车辆行驶过程中要保持安全舒适运行, 必须保证在任意t时刻满足:

|
(17) |

|
(18) |
式中,amax为最大允许横向加速度;αmax为最大允许横向加速度变化率。
求解式(17) 和式(18),得到换道行驶距离dh需满足:

|
(19) |
(1) 换道横移距离取值
1次换道横移距离等于1个车道宽度。车道宽度规定仅与设计速度有关,《公路路线设计规范》(JTG D20—2006)(以下简称《规范》)[16]中规定了高速公路不同设计速度下的车道宽度取值(表 2)。
(2) 换道过程中横向加速度取值
车辆在换道时的离心力为:

|
(20) |
式中,F为离心力;G为万有引力常量;v为汽车运行过程中的速度;R为汽车运行过程中的圆曲线半径; a为汽车运行过程中的横向加速度;重力加速度g=9.8 m/s2。
因为路面超高很小,所以车辆的横向力X满足:

|
(21) |
式中,ih为超高;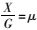
| 设计速度/(km·h-1) | 120 | 100 | 80 |
| 横向力系数 横向加速度/(m·s-2) | 0.11 0.882 | 0.12 0.98 | 0.13 1.078 |
(3) 换道过程中最大横向加速度变化率取值
横向加速度变化率是道路平、纵、横向综合作用的结果,其大小对行车舒适性影响很大。铁路上一般采用0.16~0.3 m/s3[17]。公路上因车辆尺寸较小,行驶更灵活,可采用较大的数值,美国高速公路一般采用0.61 m/s3,考虑超高的影响,修正后采用0.305 m/s3。日本[9]规定为0.5~0.75 m/s3。杨少伟等[18]采用0.5~0.6 m/s3。此外,大量研究表明,人体能承受的最大横向加速度变化率在0.4~1.0 m/s3[19],本文考虑到车道数变化处车辆运行速度略低,且为了保证车辆行驶的舒适性,因此最大横向加速度变化率取0.6 m/s3。
将参数代入式(19) 计算,可以得到不同速度下的车辆换道行驶距离(表 4)。
| 设计速度/(km·h-1) | 120 | 100 | 80 |
| 换道行驶距离/m | 210 | 175 | 140 |
2.4 确认出口距离
确认距离dc指车辆进行相关操作后驶入外侧车道并确认出口的安全距离。美国各州公路工作者协会建议,对所有车速在确定安全停车距离时,反应时间用2.5 s,在确定交叉口视距时,用2.0 s[20]。由于高速公路出口段车辆间的影响较大,为了避免驾驶人操作不便,防止驾驶人在此之前把出口标志上的内容看错,给驾驶人留有时间纠正错误,保证驾驶人安全,应限制汽车在确认段行驶时间不过短,最短应满足3 s行程,即:

|
(22) |
式中tc为确认段车辆行驶时间,本文取3 s。
2.5 标志视认距离 2.5.1 标志视认距离视认距离的大小与交通标志板上的照度、文字大小、驾驶人身体素质及车内亮度等[21]有关。天气对其影响较大,目前国内还缺乏考虑多种影响因素的研究模型和计算公式。本文采用《交通手册》的规定,在不同视力、不同速度、不同笔画数辨认率条件下的视认距离公式为:

|
(23) |
式中,d为视认距离;h为汉字高度;ac为绝对视力;c为汉字与视标的转换常数,一般取3.073 5。
《标志标线》规定指路标志汉字高度一般取值见表 5。
| 速度/(km·h-1) | 100~120 | 71~99 | 40~70 | <40 |
| 汉字高度/cm | 60~70 | 50~60 | 35~50 | 25~30 |
根据式(21) 计算得到不同字高、不同视力所需视认距离,见表 6。
| 视力/(°) | 不同汉字高度(cm)所需视认距离/m | ||
| 55 | 60 | 70 | |
| 1.5 | 185 | 201 | 235 |
| 1 | 123 | 134 | 157 |
| 0.7 | 86 | 94 | 110 |
2.5.2 标志消失距离
当汽车在标志一定距离前就看不到标志了,此距离称为消失距离。根据我国《标志标线》的规定,高速公路出口预告标志有两种设置方式(按显示位置分类),即:路侧式、车行道上方式。假设车辆处于最内侧车道,结合两种不同标志牌设置方式,由几何关系建立S的计算公式:

|
(24) |
式中,w为车道宽度;wy为硬路肩宽度;n为高速公路单向车道数;θ为驾驶人视角,直路侧式取10°[5], 车行道上方式取7°[2]。经计算得到不同车道数、不同设置方式的标志消失距离,如表 7所示。
| 设置方式 | 2车道 | 3车道 | 4车道 |
| 路侧式 | 49 | 70 | 91 |
| 车行道上方式 | 28 | 43 | 58 |
3 AGS合理设置距离
前面给出了单向2车道高速公路AGS距离的计算公式(式1)。对于单向车道数大于2的高速公路,确定AGS距离时,同样也要考虑车辆处于最不利的最内侧车道,此时,AGS距离只需要增加变换车道时的等待插入间隙行驶距离和换道行驶距离即可。则单向车道数大于等于2的高速公路AGS合理设置距离计算公式为:

|
(25) |
式中n为高速公路单向车道数。
将前述分析得到的5个行驶过程所对应的距离代入式(25),得到在驾驶人视力为1、标志牌采用路侧式或车行道上方式、不同车道数及不同设计速度条件下的AGS距离,如表 8所示。
| 单向车道数 | 2 | 3 | 4 | ||||||
| 设计速度/ (km·h-1) | 120 | 100 | 80 | 120 | 100 | 80 | 120 | 100 | 80 |
| dr/m | 67 | 56 | 44 | 67 | 56 | 44 | 67 | 56 | 44 |
| dd/m | 67 | 56 | 44 | 67 | 56 | 44 | 67 | 56 | 44 |
| dw/m | 262 | 202 | 139 | 262 | 202 | 139 | 262 | 202 | 139 |
| dh/m | 210 | 175 | 140 | 210 | 175 | 140 | 210 | 175 | 140 |
| dc/m | 100 | 83 | 67 | 100 | 83 | 67 | 100 | 83 | 67 |
| L/m | 157 | 134 | 123 | 157 | 134 | 123 | 157 | 134 | 123 |
| S/m | 49 (28) | 49 (28) | 49 (28) | 70 (43) | 70 (43) | 70 (43) | 91 (58) | 91 (58) | 91 (58) |
| AGS距离 计算值/m | 549 | 438 | 311 | 1 021 | 815 | 590 | 1 492 (1 493) | 1 179 (1 192) | 857 (869) |
| AGS距离 建议值/m | 550 | 440 | 320 | 1 030 | 820 | 600 | 1 500 | 1 200 | 870 |
| 注:括号内为标志牌采用车行道上方式时的取值, 无括号表明两种设置方式计算值相同。 | |||||||||
从表 8的计算结果可知,车道数对出口标志前置距离影响最大,而标志的设置方式对其影响较小。随着车道数的增加,高速公路AGS设置距离也相应增加。在驾驶人视力和标志牌设置方式都一定的情况下,车辆行驶速度对AGS设置距离有一定的影响,因此,为保证驾驶人安全舒适地驶离高速公路,应该按设计速度和车道数前置高速公路出口预告标志。
《标志标线》中规定高速公路出口预告标志应设置3块,当驾驶人因视线遮挡、没看清等因素错过前两块标志后,第3块(最靠近匝道出口的标志)应能给驾驶人提示前方信息,一旦错过它,驾驶人将错过正确出口,所以第3块是最重要的一块标志。表 8的AGS距离可作为第3块标志设置距离的理论依据,可解决《标志标线》中出口预告标志设置不合理、没有理论计算依据的问题。
由以上研究可知:
在实际高速公路出口预告标志设置时,第3块AGS标志应采用本文给出的建议值,前两块标志可在第3块AGS标志的基础上适当增加500 m或1 000 m,这样既能保证驾驶人视认连续性的要求,又能保证驾驶人从容换道驶离高速公路。
车道数越多,AGS距离越大,虽然满足最内侧车道上车辆的行驶要求,但是靠近外侧车道的车辆会因为前置距离过大,迟迟看不到出口而向内侧变换车道,产生无效换道行为,所以建议,AGS距离过大时可在第3块标志牌后增设相应标志牌。
4 仿真验证 4.1 仿真建模本文采用UCWin/Road进行建模,采用Forum8驾驶模拟器进行仿真。选取10名试验者,5名驾龄在2 a以上,5名驾龄在0~2 a。试验共建立10个模型,每个模型试验者驾驶1次,获取每次的心率数据和UC运行轨迹图,用心率指标来评价AGS距离对驾驶员的心、生理影响,用UC运行轨迹图来评价AGS距离的优劣。试验参数如表 9所示。
| 模型 | n=2 | n=3 | n=4 | ||||||
| 速度/
(km·h-1) | 120 | 100 | 80 | 120 | 100 | 80 | 120 | 100 | 80 |
| AGS距离/m | 550 | 440 | 320 | 1030 | 820 | 600 | 1500 | 1200 | 870 |
| 规范距离/m | 500 | 500 | 500 | 500 | 500 | 500 | 500 | 500 | 500 |
| 交通流量/
(pcu·h-1) | 1 650 | 1 600 | 1 500 | 1 650 | 1 600 | 1 500 | 1 650 | 1 600 | 1 500 |
| 试验者 | 共10名,5名驾龄在2 a以上,5名驾龄在0~2 a之间 | ||||||||
| 试验仪器 | Forum8驾驶模拟器、心率监测仪 | ||||||||
4.2 仿真结果
对180组心率数据进行分析可知,在n=2时,90%的试验者心率较平稳,AGS距离对试验者的影响较小;n=3,4,AGS小于600 m时,80%的试验者心率波动较大;AGS大于800 m时,65%的试验者心率波动较大;AGS大于1 200 m时,30%的试验者心率波动较大,AGS大于1 500 m时,5%的试验者心率波动较大。所以,在一定范围内,AGS距离越大,试验者心率波动越小,越符合驾驶员期望,AGS距离越合理。
对180组UC运行轨迹图分析可知,在n=2时,95%的试验者均可以成功驶出高速公路;n=3,4时,AGS距离为500 m的模型中,50%的试验者成功驶出高速公路;AGS距离为800~1 000 m的模型中,80%的试验者成功驶出高速公路;AGS距离为1 000~1 500 m的模型中,70%的试验者成功驶出高速公路。比较发现,500 m不能满足实际行车的需要;1 500 m和1 200 m会让驾驶员产生无效变道行为,成功驶出高速公路比例下降;600~1 000 m能满足驾驶员需求,成功驶出高速公路的比例最大。
所以仿真结果表明:仅双向四车道,《标志标线》规定的设置距离较合理;双向六车道及以上,《标志标线》规定的设置距离偏小。
5 结论(1) 基于驾驶心理学原理和驾驶人对标志的响应特性,将驶出高速公路驾驶人的操作行为过程分为5段:发现段、读取段、决策段、行动段、确认段。这些分段可保证驾驶人的安全舒适性,体现了以人为本的安全设施设计理念。
(2) 通过分析高速公路分流区交通运行状态,提出了采用移位三阶爱尔朗车头时距建立等待可插入间隙行驶距离计算模型,同时提出了基于车辆行驶连续性和舒适性的等速偏移正弦曲线车辆换道行驶距离计算模型。
(3) 建立了标志牌不同设置方式下的消失距离计算模型和AGS距离计算模型,并提出了AGS距离建议值,该建议值可作为设置第3块标志的理论支撑。结合现行《标志标线》的相关规定,同时保证驾驶人视认连续性,应在第3块标志之前设置两块标志,在其后按车道数不同而增设相应数量的标志。
(4) 本研究只考虑了小车的通行状况,对于大车比例较大的路段,没有考虑视线遮挡等情况。
| [1] | 张炜. 高速公路互通立交出口匝道安全设计与评价[D]. 南京: 东南大学, 2015. ZHANG Wei. Safety Design and Evaluation of Expressway Interchange Exit Ramp[D]. Nanjing:Southeast University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10286-1016754749.htm |
| [2] | 中国公路学会《交通工程》编委会. 交通工程手册[M]. 北京: 人民交通出版社, 2001. Traffic Engineering Editorial Board of China Highway Society. Traffic Engineering Handbook[M]. Beijing: China Communications Press, 2001. |
| [3] | GB5786-2009, 道路交通标志和标线[S]. GB5786-2009, Road Traffic Signs and Markings[S]. |
| [4] | SONG Y, LIU H, GE S. Quantitative Evaluation of the Position of an Interchange Advance Guide Sign Based on Traffic Simulation Technology[C]//14th COTA International Conference of Transportation Professionals. Changsha:ASCE, 2014:2653-2659. |
| [5] | 郭唐仪, 胡启洲, 姚丁元. 高速出口预告指路标志设置距离及其安全性能比较[J]. 公路交通科技, 2011, 28(12): 106-111 GUO Tang-yi, HU Qi-zhou, YAO Ding-yuan. Comparison of Placement Distances of Advance Guide Sign of Freeway Exit and Their Safety Performances[J]. Journal of Highway and Transportation Research and Development, 2011, 28(12): 106-111 |
| [6] | 刘伟铭, 邓如丰, 张阳, 等. 高速出口前置指路标志的安全距离设置模型[J]. 华南理工大学学报:自然科学版, 2013, 41(2): 37-43 LIU Wei-ming, DENG Ru-feng, ZHANG Yang, et al. Setting Model of Safe Distance of Advance Guide Signs at Highway Exits[J]. Journal of South China University of Technology:Natural Science Edition, 2013, 41(2): 37-43 |
| [7] | 崔洪军, 马新卫, 李霞, 等. 高速公路出口前置指示标志安全距离计算模型[J]. 公路交通科技, 2016, 33(4): 120-126 CUI Hong-jun, MA Xin-wei, LI Xia, et al. A Model for Calculating Advance Guide Sign's Reasonable Setting Location at Expressway Exit[J]. Journal of Highway and Transportation Research and Development, 2016, 33(4): 120-126 |
| [8] | 李爱增, 李文权, 王炜. 城市快速路出口标志位置设置研究[J]. 交通运输系统工程与信息, 2006, 6(5): 36-41 LI Ai-zeng, LI Wen-quan, WANG Wei. Research on Position of Traffic Sign on Urban Expressway Off-ramp[J]. Journal of Transportation Systems Engineering and Information Technology, 2006, 6(5): 36-41 |
| [9] | 日本道路工团. 日本高速公路设计要领[M]. 交通运输部工程管理司, 译. 西安: 陕西旅游出版社, 1991. Japan Highway Public Corporation. Expressway Design Essentials of Japan[M]. Project Management Division of Ministry of Transportation, translated. Xi'an:Shaanxi Tourism Press, 1991. |
| [10] | 刘志玮. 高速公路合流区交通模拟与评价研究[D]. 西安: 西北工业大学, 2004. LIU Zhi-wei. Study on Traffic Simulation and Evaluation of Expressway Traffic Zone[D]. Xi'an:Northwestern Polytechnical University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10359-2005011933.htm |
| [11] | JTGB01-2014, 公路工程技术标准[S]. JTGB01-2014, Technical Standard of Highway Enginee-ring[S]. |
| [12] | 孔令臣. 多车道高速公路互通式立交加减速车道长度及最小净距研究[D]. 西安: 长安大学, 2012. KONG Ling-chen. Study on Length of Acceleration and Deceleration Lanes and Minimum Distance of Multi Lane Expressway Interchange[D]. Xi'an:Chang'an University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10710-1013017489.htm |
| [13] | 杨志刚, 戚志锦, 黄燕. 智能车辆自由换道轨迹规划研究[J]. 重庆交通大学学报:自然科学版, 2013, 32(3): 520-524 YANG Zhi-gang, QI Zhi-jin, HUANG Yan. Trajectory Planning of Lane Changing for Intelligent Vehicles[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2013, 32(3): 520-524 |
| [14] | 李玮, 高德芝, 段建民. 智能车辆自由换道模型研究[J]. 公路交通科技, 2010, 27(2): 119-123 LI Wei, GAO De-zhi, DUAN Jian-min. Research on Lane Change Model for Intelligent Vehicles[J]. Journal of Highway and Transportation Research and Development, 2010, 27(2): 119-123 |
| [15] | 杨建国, 王金梅, 李庆丰, 等. 微观仿真中车辆换道的行为分析和建模[J]. 公路交通科技, 2004, 21(11): 93-97 YANG Jian-guo, WANG Jin-mei, LI Qing-feng, et al. Behavior Analysis and Modeling of Lane Change in Traffic Micro-simulation[J]. Journal of Highway and Transportation Research and Development, 2004, 21(11): 93-97 |
| [16] | JTG D20-2006. 公路路线设计规范[S]. JTG D20-2006. Design Specifications for Highway Alignment[S]. |
| [17] | 邢志辉. 道路线形舒适性中横向加速度变化率模型分析[J]. 河北工业大学学报:社会科学版, 2009, 24(2): 39-41 XING Zhi-hui. Model Analysis on Change Rate of Horizontal Acceleration in Line Shape Comfortableness of Road[J]. Journal of Hebei University of Technology:Social Science Edition, 2009, 24(2): 39-41 |
| [18] | 杨少伟. 道路勘测设计[M]. 3版. 北京: 人民交通出版社, 2009. YANG Shao-wei. Road Survey and Design[M]. 3rd ed. Beijing: China Communications Press, 2009. |
| [19] | 佘守宪, 赵雁. 加加速度(加速度的时间变化率):冲击、乘座舒适性、缓和曲线[J]. 物理与工程, 2001, 11(3): 7-12 SHE Shou-xian, ZHAO Yan. Jerk (the Time Rate of Change of Acceleration):Impact, Passenger's Comfor-tability, Transition Curve[J]. Physics and Engineering, 2001, 11(3): 7-12 |
| [20] | 任福田, 刘小明, 荣建. 交通工程学[M]. 北京: 人民交通出版社, 2008. REN Fu-tian, LIU Xiao-ming, RONG Jian. Traffic Engineering[M]. Beijing: China Communications Press, 2008. |
| [21] | 赵炜华, 王丽华, 叶飞, 等. 驾驶人所处环境照度对视认距离影响[J]. 交通信息与安全, 2013, 31(6): 11-16, 22 ZHAO Wei-hua, WANG Li-hua, YE Fei, et al. Impacts of Environmental Luminosity around Driver on Distance of Visual Cognition[J]. Traffic Information and Safety, 2013, 31(6): 11-16, 22 |
 2017, Vol. 34
2017, Vol. 34
