扩展功能
文章信息
- 徐洁琼, 姚佼, 倪枫
- XU Jie-qiong, YAO Jiao, NI Feng
- 城市干道的多时段协调控制优化
- Arterial Time-of-day Coordinated Control Optimization in Urban Area
- 公路交通科技, 2017, 34(8): 114-122, 129
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(8): 114-122, 129
- 10.3969/j.issn.1002-0268.2017.08.016
-
文章历史
- 收稿日期: 2016-10-12
自J. T. Morgan,J. D. C. Little等[1-2]建立最大绿波带宽混合整数线性规划MAXBAND模型以来,国内外学者对城市干道绿波协调控制优化的研究不断深入。卢守峰等[3]将交通流离散公式植入MAXBAND模型,以改善该模型中路段行驶时间简单取为样本车辆路段行驶时间算术平均值的不足。曹交交等[4]针对MAXBAND模型无法适应交通流的随机性和双向交通流的不均衡性的现状,建立了以干线双向绿波到达交叉口的时刻差值最小为目标的交通干线信号动态优化控制模型。Gartner等针对不同路段交通流量、通行条件以及带宽需求的不同,在MAXBAND模型的基础上提出了可变带宽的干道绿波协调控制模型——MULTIBAND模型,通过加入路网闭环约束条件,将模型的应用范围扩展到城市干道网区域协调控制,能基本适应交通信号协调控制的实时性要求[5-7]。虽然比MAXBAND更能发挥可变带宽协调控制的实时性优势,但MUTIBAND绿波带按中心线严格对称的特点和绿灯时段内的不合理位置,容易造成绿波不稳定。唐克双等[8]针对MULTIBAND模型的这一特点,提出了非对称式绿波,增加绿波带位置的约束,以提高绿波运行稳定性。然而,这并不能避免排队车辆较多的情况下对主路绿波的影响。无论是MAXBAND模型还是MULTIBAND模型,对模型参数准确度依赖较高,且并未针对每天不同时段交通流量变化的潮汐特点制订相应的信号优化方案,在交通控制上仍有改善空间。T. M. Brennan Jr.等[9]考虑到干道协调控制系统正常运行需要保证250个参数的正确性,容错率较低,建立了对协调控制系统正常工作进行监测与辅助的可视化工具,然而该工具尚未集成到控制系统中,不能为日常交通控制策略服务。
在干道协调控制优化模型的求解方面,卢凯等[10]提出了一种进口单独放行方式下的干道双向绿波协调控制数解算法,以保证不同干道行驶方向的理想绿波带宽度。卢顺达等[11]对经典的双向绿波图解法进行了优化,以提升绿波协调控制效果;宋晓鹏等[12]利用非支配排序遗传算法建立了城市干道动态绿波控制模型。但上述方法实行效率较低,不适合大范围地运用于我国城市交通控制当中。
目前最适宜我国交通发展现状的稳定控制方式当属多时段控制(TOD),近年来在TOD领域的研究中,J.Yang等[13]通过Kohenen聚类和K均值聚类在多时段方案切换时刻优化效率的比较,证明了K均值在聚类中的卓越效益,但K均值聚类需提前指定聚类个数及初始聚类中心,导致陷入局部最优。N. T. Ratrout[14]通过采用减法聚类和K均值聚类结合的方式寻找最优切换时刻,但对“噪声”较敏感。姚佼等以改进立方群准则作为聚类终止条件,运用Ward最小方差法及混合聚类算法进行了聚类分析[15-16],然而,以上方法只用于单点控制,对干道协调控制的适用性有待进一步研究。
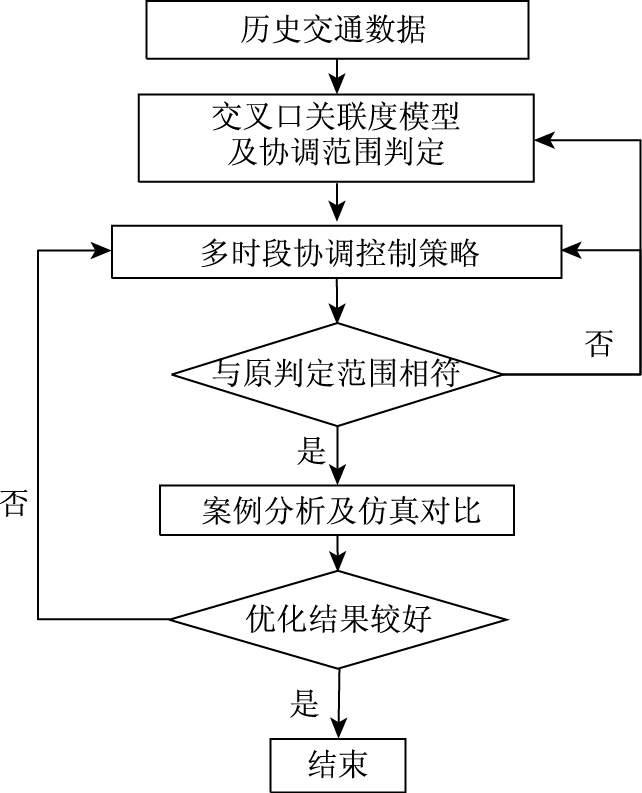
本研究基于干道交叉口关联度分析,对干道协调的边界进行划定,进而对协调范围内的交叉口流量分别进行混合聚类处理,基于其时序性规律,得到相应的多时段控制方案。此外,多时段控制方案的切换会对交通流带来干扰,即使信号控制方案的切换过渡对交通流造成的影响是短暂的,却可以使得控制系统性能急剧下降[17-18],并对信号控制效果产生一段时间的负面影响[19]。基于此项考虑,本文通过尽可能扩大协调控制带宽的方式,使干道行驶的车辆通过相邻交叉口遇到相同控制方案,减少干道车流进行信号过渡的次数。以干道车均延误最小、干道带宽最大为目标,建立模型,并用粒子群智能优化算法对其进行求解,得到普遍适用于我国城市交通现状且高效稳定的干道多时段协调控制优化方案。最后通过实际案例进行仿真验证,具体流程如图 1所示。
|
| 图 1 干道多时段协调控制策略流程图 Fig. 1 Flowchart of arterial road time-of-day coordinated control strategy |
| |
1 交叉口关联度计算 1.1 交叉口关联度模型
通过交叉口关联度计算,确定上下游交叉口之间的关联程度,并以此为依据,对目标干道是否进行协调及协调边界作出决断。
交叉口间的关联度可通过对Synchro内嵌模型[20]进行改进,如式(1) 所示:
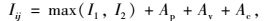
|
(1) |
式中,Iij为交叉口群连线间的关联度;I1为以自由行程时间为主要考量因素得到的关联系数;I2为以道路饱和程度为主要考量因素得到的关联系数;Ap为车辆到达离散程度调整系数;Av为道路流量调整系数;Ac为两交叉口信号周期调整系数。
式(1) 中各参数由式(2) 到式(13) 确定。I1的计算式为:
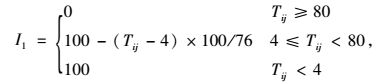
|
(2) |
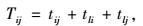
|
(3) |
式中,Tij为交叉口i到j的行程时间;tij为无排队长度情况下,车流从交叉口i到j的平均行程时间;tli,tlj分别为交叉口i和交叉口j的排队长度对行程时间的折算,计算方法为:
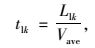
|
(4) |
式中,Llk为交叉口k的排队长度;Vave为该路段的平均行驶速度。
I2的取值为:
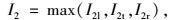
|
(5) |
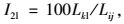
|
(6) |
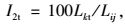
|
(7) |
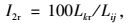
|
(8) |
式中,Lkl,Lkt,Lkr分别为k交叉口左转车道、直行车道和右转车道的排队长度;Lij为i与j交叉口的间距。
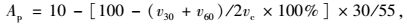
|
(9) |
式中,v30为每信号周期的30%内车辆到达密集程度最高时的车流量;v60为每信号周期的60%内车辆到达密集程度最高时的车流量;vc为每周期到达车流量。
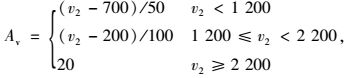
|
(10) |
式中v2为待考察交叉口之间路段的双向流量。
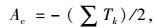
|
(11) |
式中,
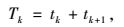
|
(12) |
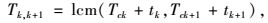
|
(13) |
Tk为k交叉口为协调而增加的最小信号周期差;Tk, k+1为k交叉口与k+1交叉口间协调后周期的最小公倍数;tk,tk+1分别为k交叉口与k+1交叉口为协调而增加的最小信号周期差。
1.2 基于关联度模型的协调控制边界范围确定若交叉口关联度系数Iij≤20则无需协调;Iij≥80则必须协调[20],当协调系数取值范围在20至80时,考虑多时段不同控制方案的特点,通过构建隶属度函数,对是否协调做出决策。
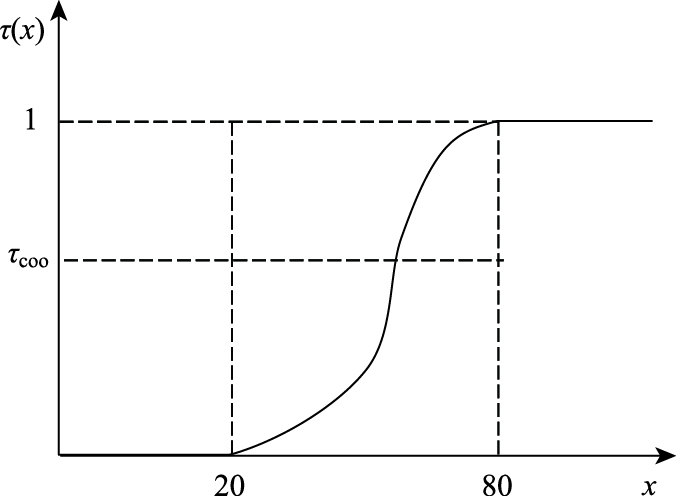
首先,设协调程度函数取值τ为连续值,论域为[0, 1]。由于交叉口关联度协调模型计算所得协调系数是由许多微小的独立随机因素影响的结果,根据中心极限定理可以将其视为正态分布[21-22],对传统隶属度函数[23]进行改进,构造的隶属度函数,如式(14) 和图 2所示。其中,x为1.1节关联度模型计算得到的协调系数,此处作为隶属度函数的自变量输入。
|
| 图 2 交叉口协调控制策略隶属度函数 Fig. 2 Membership function of intersection coordinated control strategy |
| |
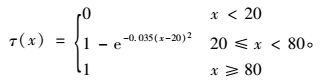
|
(14) |
对于协调与否的判断,相关研究表明,交通流量越大,协调控制的意义越大而且越必要[24]。因此,协调程度隶属度函数需设定一阈值τcoo,当隶属度τ(x)≥τcoo时,则可判定为协调[25],其定义如式(15) 所示:
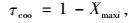
|
(15) |
式中,Xmaxi为多时段控制第i个方案运营期间两交叉口的最大饱和度。当流量随着多时段方案变化而增大时,τcoo的取值也越小。
确定具体的协调控制边界范围时,首先基于上述判断方法,将干道各交叉口的历史交通流量数据输入关联度模型。考虑到多时段协调控制可能会对干道协调范围内各交叉口的信号配时方案进行修改,之后的交叉口信号控制情况可能不再适合原协调范围,因此,需再次进行干道交叉口间关联度计算,并作出协调范围判定。若该范围有变,则对该交叉口关联度模型、多时段控制策略模型进行相应核查与修改,直至问题解决;若该范围保持不变,则协调范围判定结束。
2 干道多时段协调控制策略对需进行干道协调控制的各交叉口,首先分别进行快速聚类与系统聚类相结合的混合聚类多时段划分处理,得到各交叉口全天多时段控制方案。在此基础上,将干道关联交叉口的同方案时段作为同一方案带宽的划分依据,使得以平均车速行驶的车辆通过协调交叉口时,经历同一控制方案,此时对车流的扰动最小,控制效果也最好。进而将方案带宽最大与干道车均延误最小作为优化目标,采用多目标智能优化算法,得到使得干道扰动最小、控制效果最好的干道协调控制方案。
2.1 交叉口历史交通流量数据混合聚类对协调范围内各交叉口的历史交通流量数据进行混合聚类处理,将快速聚类前期收敛快和系统聚类精度高的特点有机结合,高效而精准地得到各交叉口全天24 h的多方案时段划分情况。具体而言,快速聚类步骤如下:
(1) 选取初始聚类个数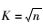
(2) 根据各初始类中的元素,分别计算各类的重心,作为初始凝聚点。
(3) 将所有样本按距离最近原则(本研究采用欧式距离)进行二次聚类,重新归入距离最小的类中,并以此时每类中所包含的新样本的均值作为该类的中心。
(4) 计算n个样本到新中心的距离,重复步骤(3) 再次归类。
(5) 重复步骤(3) 和(4),直到快速聚类结果不再变化,快速聚类部分结束,并将其最终分类结果作为系统聚类的初始类。
系统聚类的步骤如下:
(1) 选取Silhouette指标[27]作为系统聚类的终止条件,Silhouette指标最大值所对应的聚类个数即为最佳聚类个数。
(2) 依据各初始类的类间距离平方,对距离最近的两个类合并成一新类。
(3) 计算该类与其他类的类间距离。
(4) 重复系统聚类步骤(1) 和(2),继续对两个距离最近的类进行合并,每次减少1类,直至达到最佳聚类个数,混合聚类结束。
根据历史交通流量数据分类情况,结合交通流时序性规律,分别制订协调范围内相应时段的交通控制方案。
2.2 多目标协调控制优化模型由于信号控制方案频繁切换会对交通流造成扰动,不同交叉口方案切换的时刻差也可能引发蝴蝶效应,对流量较大的干道造成不利交通影响。不同交叉口方案切换的时刻差越少,对多时段控制协调控制而言,意味着干道车流行驶过程中遭遇的方案切换次数越少,并且全天总控制策略的方案带宽W最大。另一方面,城市干道在不同时间段车流量状况不同,交叉口环境状况不同,车辆平均延误最能反映交通控制策略对城市道路车辆的影响。因此,选取方案总带宽W和干道平均车辆延误D为干道多时段协调控制模型的目标函数:
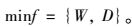
|
(16) |
根据不同时段的交叉口流量特点对多目标优化的带宽和延误权重进行考虑,即在高峰时期,主要考虑主干路通过能力尽可能大,即带宽的权重较大;在平峰和低谷时期,则主要考虑交叉口的车均延误,故延误的权重较大[24]。在假设通行能力不变的情况下,将饱和度作为两者权重的划分依据,即带宽的权重为:
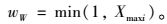
|
(17) |
延误的权重为:
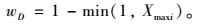
|
(18) |
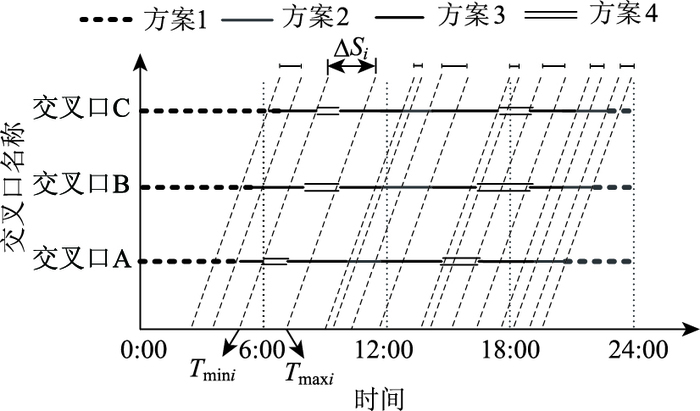
方案总带宽W计算方式如式(19) 至式(23) 和图 3所示:
|
| 图 3 控制方案带宽计算示意图 Fig. 3 Schematic diagram of calculating bandwidth of control scheme |
| |
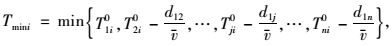
|
(19) |
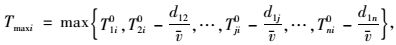
|
(20) |
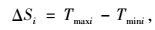
|
(21) |
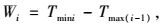
|
(22) |
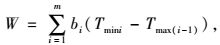
|
(23) |
式中,Wi为方案i的带宽;W为方案总带宽;bi为i方案时期的交通流量占全天交通总流量的比值,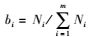
干道平均车辆延误的计算根据阿克赛力科以及罗伯逊的论述,在协调控制情况下采用过渡函数模型的方法[28],表示为:
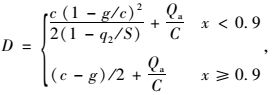
|
(24) |
式中,D为干道平均车辆延误;Qa为平均过饱和排队长度(包括车辆到达率随机波动构成的排队长度,排队状态下的车头间距取9 m[29];g为有效绿灯时间;c为信号周期时长;S为饱和流量;C为相位通行能力。
下游断面在第j个时间段的车流到达率为:
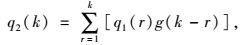
|
(25) |
式中,q2(k)为在时间段k到达下游交叉口停车线的车流流率;q1(r)为在时间段r上游停车线断面车流的驶出流率;g(k-r)为从上游停车线断面到下游某断面行驶时间为(k-r)的车辆概率分布函数,是一种变换了的正态分布函数,按式(26) 计算:
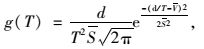
|
(26) |
式中,T为车辆行驶时间;d为下游某断面与上游停车线之间的距离;V为车流的平均行驶速度;S为车流中不同车辆所具有的行驶速度的标准差。
平均过饱和排队长度的计算式为:
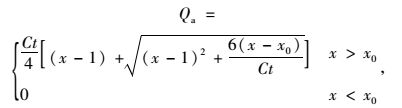
|
(27) |
式中,t为研究时段;x为该相位饱和度;x0为延误模型中给定的划分指标,取值为:
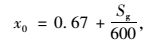
|
(28) |
式中Sg为绿灯时间通行车辆数。
2.3 模型求解显然,上述多时段干道协调优化模型为多目标优化问题,其中的子目标为“延误最小”和“方案带宽最大”,任一子目标的改善都可能引起另一子目标性能降低,使子目标都到达最优显然难以通过传统单目标优化方法实现。因此,此处选用多目标智能优化算法对以上多目标模型进行求解。
文中多时段协调优化模型为高维多目标模型,且考虑到需要输入和处理大量历史交通流量信息,因此,选用多目标粒子群算法(MOPSO)进行模型求解[30-31]。步骤如下:
(1) 初始化粒子群算法中的粒子数M。对每个粒子,依据优化前的多时段干道策略中的绿信比、相位差、方案切换时刻等确定其初始位置P0和零初始速度V0、初始化惯性因子ω、学习因子C1和C2、最大迭代次数Nmax,并据此计算每个粒子对于协调带宽及车均延误的目标向量。
(2) 将粒子群M中的部分粒子保存在外部粒子群中,这些粒子的位置即为非劣解。
(3) 将目标空间分割成若干储存空间,根据粒子所对应的目标向量确定每个粒子所在的存储空间。
(4) 为每个至少包含1个外部粒子群个体的存储空间定义适应度值(等于或大于1的数与格子内所包含的NP成员个数之比),然后对每个粒子,根据轮盘赌方法选择1个存储空间,并从中随机选择1个外部粒子群的个体作为粒子的局部最优解gbest。
(5) 更新粒子的全局最优解Pbest。根据粒子飞行过程中获得的新解与其自身最好位置Pbest比较,若新解支配了Pbest,则新解为新的Pbest;否则,Pbest保持不变;若新解与Pbest彼此不受支配,则从两者随机选择1个作为新的自身最好位置。
(6) 利用公式迭代更新所有粒子的位置和速度,则粒子i在第k+1次迭代后的速度Vik+1与位置Pik+1由其在第k次迭代后的速度Vik与位置Pik计算得到:
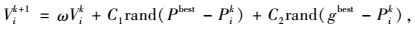
|
(29) |
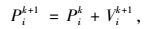
|
(30) |
式中,rand()函数取值为[0, 1]之间的随机数。
(7) 采用如下措施以避免粒子飞出搜索空间:一旦粒子飞出了某个决策变量的边界,该粒子停留在该边界上,同时改变飞行方向。
(8) 计算粒子群P中每个粒子的目标向量,继续迭代,如果适应值降低程度小于规定阈值[32],则停止搜索;否则,转到(6)。
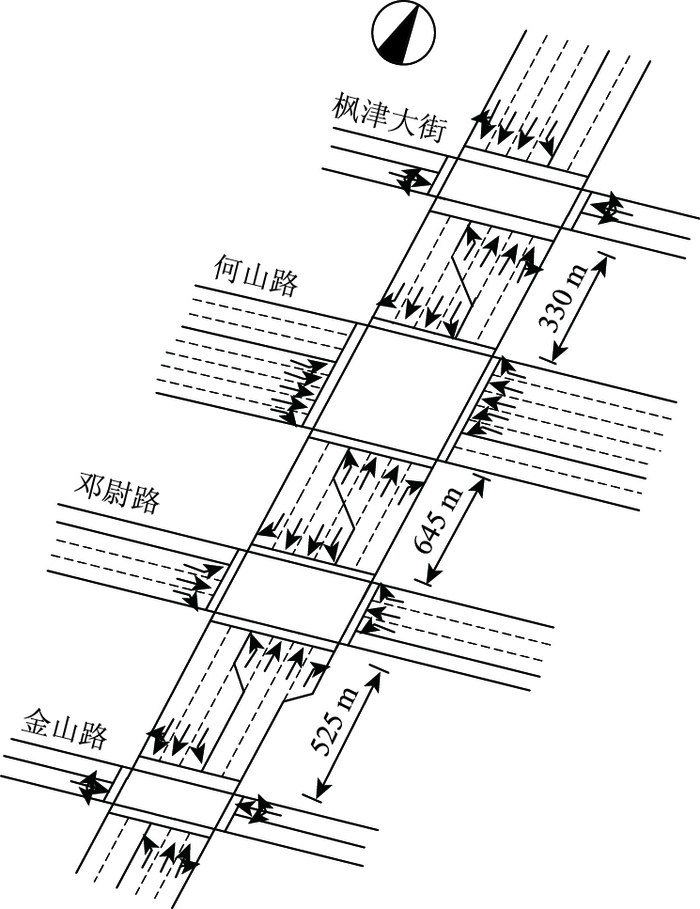
3 案例分析为对本研究的成果进行验证,选取江苏省苏州市虎丘区主干道滨河路上的枫津大街、何山路、邓尉路及金山路4个交叉口作为研究对象进行仿真,道路与交叉口空间布局如图 4所示。其交通流状态稳定,时段差异明显,适合进行多时段及协调控制。本研究基于2016-03-13至2016-04-13共19个工作日的24 h交通流量数据,数据精度为5 min。数据采集单元为流量线圈检测器,数据来源于苏州市智能交通管理指挥系统的自适应交通控制子系统。
该道路现状交通控制方式为系统线控,全天采用方案数为3,各交叉口方案切换时刻相同,具体配时如表 1所示。
| 编号 | 方案1 | 方案2 | 方案3 |
| 名称 | 晚低峰 | 平峰 | 早高峰、晚高峰 |
| 符号 |
 |  |
 |
| 时段 | 19:00—7:30 | 8:40—17:00 | 7:30—8:40 17:00—19:00 |
根据Silhouette指标值计算可得,交通控制方案数为3时可达到最优流量聚类效果。关联度指标计算情况及协调范围划分情况如表 2所示。
|
| 图 4 滨河路干道沿线交叉口布局 Fig. 4 Configuration of intersections along arterial road of Binghe Road |
| |
| 控制 策略 | 枫津大街-何山路 | 何山路-邓尉路 | 邓尉路-金山路 | ||||||
| 方案号 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 关联 指标 | 87 | 89 | 101 | 66 | 76 | 78 | 52 | 79 | 83 |
由表 2可知,由于滨河路交叉口关联紧密,关联度指标均大于80,故而应当全天进行协调控制。何山路-邓尉路路段全天时段,邓尉路-金山路路段方案1、方案2关联度系数未达80,此时的协调系数值由式(14) 计算而得均趋近于1,通过隶属度计算与比较可得,研究路段4个交叉口全天均应进行协调控制。
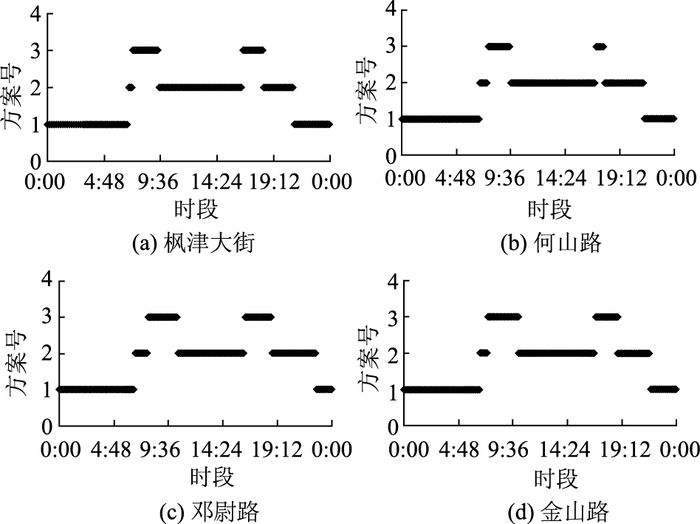
采用2.1节的混合聚类方法,基于交通流时序性特征对各交叉口控制方案进行划分,结果如图 5所示。
|
| 图 5 基于混合聚类的各交叉口多时段控制方案 Fig. 5 Time-of-day control scheme of intersections based on mixed clustering |
| |
在混合聚类多时段控制方案的基础上,对多时段协调控制优化模型进行求解。多目标粒子群算法中各参数取值[26]如表 3所示。
| 参数 | M | C1 | C2 | ω | Nmax |
| 取值 | 40 | 2 | 2 | 0.5 | 1 000 |
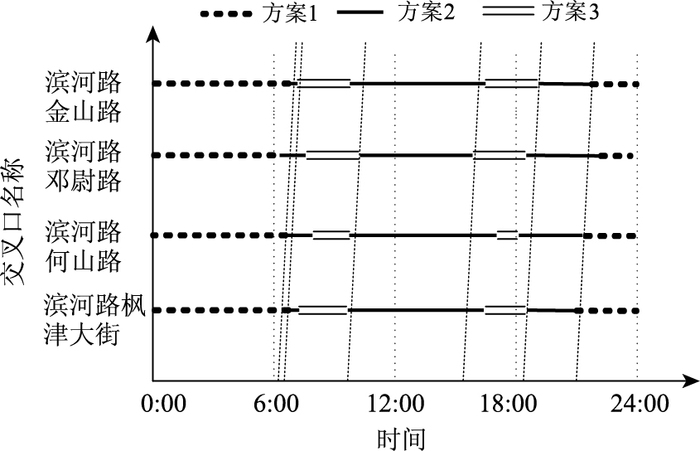
优化后的各交叉口协调控制方案如图 6所示。
|
| 图 6 干道协调优化模型求解的多时段控制方案 Fig. 6 Time-of-day control scheme solved by arterial road coordinated optimization model |
| |
综合以上结果,可以得到滨河路干道研究范围内4交叉口现状方案、混合聚类优化方案、多时段协调控制优化方案的运行时段,如表 4所示。
| 方案号 | 1 | 2 | 3 | |
| 时段 | 晚低峰 | 平峰 | 早高峰、晚高峰 | |
| 符号 |
|

|

| |
| 枫津 大街 | 现状 方案 | 19:00—7:30 | 8:40—17:00 | 7:30—8:40 17:00—19:00 |
| 聚类优 化方案 | 20:55—6:55 | 6:55—7:15 9:30—16:35 18:20—20:55 | 7:15—9:30 16:35—18:20 | |
| 协调优 化方案 | 21:40—6:55 | 6:55—7:25 9:45—16:45 17:40—21:40 | 7:25—9:45 16:45—17:40 | |
| 何山路 | 现状 方案 | 19:00—7:30 | 8:40—17:00 | 7:30—8:40 17:00—19:00 |
| 聚类优 化方案 | 21:20—6:55 | 6:55—7:40 9:35—17:05 17:50—21:20 | 7:40—9:35 17:05—17:50 | |
| 协调优 化方案 | 21:40—6:55 | 6:55—7:25 9:50—16:50 18:10—21:40 | 7:25—9:50 16:50—18:10 | |
| 邓尉路 | 现状 方案 | 19:00—7:30 | 8:40—17:00 | 7:30—8:40 17:00—19:00 |
| 聚类优 化方案 | 22:35—6:40 | 6:40—7:50 10:25—16:20 18:40—22:35 | 7:50—10:25 16:20—18:40 | |
| 协调优 化方案 | 21:40—7:00 | 7:00—7:25 9:55—16:50 17:50—21:40 | 7:25—9:55 16:50—17:50 | |
| 金山路 | 现状 方案 | 19:00—7:30 | 8:40—17:00 | 7:30—8:40 17:00—19:00 |
| 聚类优 化方案 | 21:40—6:45 | 6:45—7:25 10:05—16:45 18:45—21:40 | 7:25—10:05 16:45—18:45 | |
| 协调优 化方案 | 21:45—6:40 | 6:40—7:25 9:55—16:50 18:10—21:45 | 7:25—9:55 16:50—18:10 | |
可以看出,现状方案虽然全天为3个方案,但方案切换次数较少,早晚高峰与早晚低峰之间切换较为突兀。相比之下,聚类优化方案通过混合聚类处理,将早高峰前、晚高峰后与早晚高峰区别开,采用平峰期方案进行过渡,处理更为精细。多时段协调控制优化方案在聚类优化方案的基础上,将滨河路上的4个交叉口在方案切换时刻上进行协调控制,使得车流通过该道路4个交叉口时,最大可能地通过遇到相同控制方案,降低延误和遇到不同方案时对车流的扰动。
滨河路干道研究范围内4交叉口现状方案、混合聚类优化方案、多时段协调控制优化方案的控制效益如表 5所示。
| 控制 方案 | 方案号 | 时段 名称 | 带宽/
(5 min) | 总带宽/
(5 min) | 车均延 误/s | 总延 误/s |
| 现状控 制方案 | 1 | 晚低峰 | 149.55 | 38.81 | 7.64 | 27.32 |
| 2 | 平峰 | 99.55 | 18.86 | |||
| 3 | 早高峰、晚高峰 | 18.71 | 41.56 | |||
| 混合聚 类优化 控制方 案 | 1 | 晚低峰 | 97.00 | 31.73 | 7.64 | 24.47 |
| 2 | 早高峰前、平 峰、晚高峰后 | 35.82 | 16.33 | |||
| 3 | 早高峰、晚高峰 | 14.46 | 36.27 | |||
| 多时段 协调优 化控制 方案 | 1 | 晚低峰 | 107.10 | 39.19 | 7.40 | 23.87 |
| 2 | 早高峰前、平 峰、晚高峰后 | 45.02 | 16.34 | |||
| 3 | 早高峰、晚高峰 | 19.16 | 35.16 | |||
| 注:此处总带宽与总延误为与全天流量加权平均后的结果。 | ||||||
从表 5中可以看出,就全天多时段控制方案而言,经过混合聚类优化后的多时段控制方案车均总延误较现状方案下降10.43%,总带宽却减少18.24%;协调优化方案与现状方案相比,延误下降12.63%,总带宽增加0.98%;与混合聚类方案比较延误下降2.45%,总带宽增加23.51%。具体到各个不同时段:
(1) 早晚高峰时期延误优化效果较为明显,其中混合聚类优化方案使延误下降12.72%,协调优化方案较现状方案使延误下降15.40%,较混合聚类优化方案下降3.06%。主要原因是在控制方案数不变的情况下,聚类优化方案将全天时段划分更精细,增加了早高峰前和晚高峰后的时段划分,对这个时期进行单独考虑,使得高峰时期到低峰时期有自然过渡;而协调控制方案在此基础上通过优化干道相关交叉口的方案切换时刻,使车辆在同一方案下通过该道路,对高峰时期大流量车流扰动的冲击进一步降低。在带宽方面,由于混合聚类优化方案以每个交叉口的历史交通流量及交通时序规律进行控制方案划分,以本交叉口效益最优为前提,故而协调控制效果不够理想,使得带宽较现状方案减少22.72%;协调优化方案经过交叉口之间切换时刻的相互妥协,使现状方案带宽增加2.41%。
(2) 平峰及早高峰前、晚高峰后时期,在车均延误方面,混合聚类方案通过精确到5 min的控制划分方式,将相应信号控制方案发挥到最大效益,使得降低延误13.41%,而协调控制需要兼顾上下游交叉口全局,在平峰时期的控制效益稍逊于混合聚类方案,降低延误13.34%。而由于现状控制方案的方案切换较少,4个路口一刀切的模式虽然使得带宽增大,但对干道造成的扰动和延误较大。此时期的协调优化控制方案较混合聚类优化方案带宽增加25.68%。
(3) 晚低峰时期车流量较少,此时的延误主要来自于信号控制造成的车辆等待,混合聚类优化控制方案对流量少且分布差异不明显的情况优化效果不明显,而协调优化控制则通过对控制范围内交叉口的协调,使得车辆在通过4个交叉口的总等待时间减少,进而降低车均延误3.14%。此时协调优化控制方案与混合聚类优化控制方案相比,方案带宽增加10.41%。
4 结论城市干道多时段协调控制充分发挥多时段控制稳定性高且成本低的特点,使得协调控制在降低车辆停车率及频繁地方案切换造成扰动的同时,降低车均延误。本研究在交叉口关联度确定协调范围的基础上,首先运用混合聚类方式对协调范围内交叉口的历史交通流量进行快速高效的方案分类,进而以协调带宽和车均延误作为优化目标,运用多目标智能优化求解算法,得出干道多时段协调的最优控制方案。通过研究可得以下结论:
(1) 混合聚类优化方案可以有效降低车均延误,但由于其以车均延误降低为优化目标,可能导致车辆在干道行驶过程中,在不同交叉口遇到不同的控制方案,对车队造成扰动,不利于协调控制。
(2) 在混合聚类优化方案对干道上交叉口分别优化控制方案的前提下,协调控制优化方案进行协调控制优化,其结果表明,协调控制优化方案既能有效降低车均延误,又能保证协调带宽。
(3) 协调控制优化方案在高峰时期的控制效益改善程度优于非高峰时期。
由于时间及篇幅原因,本文未探讨过饱和情况下该信号优化策略的效果,且未对方案过渡时刻及其扰动所带来的延误进行具体计算,需在后续研究中进一步深入探讨。
| [1] | MORGAN J T, LITTLE J D C. Synchronizing Traffic Signals for Maximal Bandwidth[J]. Operations Research, 1964, 12(6): 896-912 |
| [2] | LITTLE J D C, KELSON M D, GARTNER N H. Maxband:A Program for Setting Signals on Arteries and Triangular Networks[J]. Transportation Research Record, 1981, 795: 40-46 |
| [3] | LIU X, DAI S, LU S. Revised MAXBAND Model for Bandwidth Optimization of Traffic Flow Dispersion[C]//ISECS International Colloquium on Computing, Communication, Control, and Management. Guangzhou:IEEE, 2008:85-89. |
| [4] | 曹交交, 韩印, 姚佼. 城市交通干线动态双向绿波优化控制模型[J]. 公路交通科技, 2015, 32(9): 115-120 CAO Jiao-jiao, HAN Yin, YAO Jiao. A Dynamic Dual-direction Green Wave Optimization Control Model for Urban Arterial Roads[J]. Journal of Highway and Transportation Research and Development, 2015, 32(9): 115-120 |
| [5] | GARTNER N H, ASSMANN S F, LASAGA F, et al. MULTIBAND:A Variable-bandwidth Arterial Progression Scheme[J]. Transportation Research Record, 1990, 1287: 212-222 |
| [6] | GARTNER N H, ASSMAN S F, LASAGA F, et al. A Multi-band Approach to Arterial Traffic Signal Optimization[J]. Transportation Research Part B:Methodological, 1991, 25(1): 55-74 |
| [7] | STAMATIADIS C, GARTNER N H. MULTIBAND-96:A Program for Variable-bandwidth Progression Optimization of Multiarterial Traffic Networks[J]. Transportation Research Record, 1996, 1554: 471-471 |
| [8] | 唐克双, 孔涛, 王奋, 等. 一种改进的多带宽干线协调控制模型[J]. 同济大学学报:自然科学版, 2013, 41(7): 1002-1008 TANG Ke-shuang, KONG Tao, WANG Fen, et al. A Modified MULTIBAND Model for Urban Arterial Coordinate Control[J]. Journal of Tongji University:Natural Science Edition, 2013, 41(7): 1002-1008 |
| [9] | BRENNAN T M, J r, DAY C M, STURDEVANT J R, et al. Visual Education Tools to Illustrate Coordinated System Operation[J]. Transportation Research Record, 2011, 2259: 59-72 |
| [10] | YOU X, LI L, MA W. Coordinated Optimization Model for Signal Timings of Full Continuous Flow Intersections[J]. Transportation Research Record, 2013, 2356: 23-33 |
| [11] | MA W, XIE H, LIU Y, et al. Coordinated Optimization of Signal Timings for Intersection Approach with Presignals[J]. Transportation Research Record, 2013, 2355: 93-104 |
| [12] | 卢凯, 徐建闽, 李轶舜. 进口单独放行方式下的干道双向绿波协调控制数解算法[J]. 中国公路学报, 2010, 23(3): 95-101 LU Kai, XU Jian-min, LI Yi-shun. Algebraic Method of Arterial Road Coordinate Control for Bidirectional Green Wave under Signal Design Mode of One-phase-one-approach[J]. China Journal of Highway and Transport, 2010, 23(3): 95-101 |
| [13] | YANG J, YANG Y. Optimization of Time of Day Break Points of Intersection Using Cluster Method[J]. International Journal of Advancements in Computing Technology, 2013, 5(6): 479-487 |
| [14] | RATROUT N T. Subtractive Clustering-based K-means Technique for Determining Optimum Time-of-day Breakpoints[J]. Journal of Computing in Civil Engineering, 2010, 25(5): 380-387 |
| [15] | 姚佼, 徐洁琼, 韩印. 基于聚类分析的城市交通TOD控制的优化方法研究[J]. 交通运输工程学报, 2014, 14(6): 110-116 YAO Jiao, XU Jie-qiong, HAN Yin. TOD Optimal Control Method of Urban Traffic Based on Clustering Analysis[J]. Journal of Traffic and Transportation Engineering, 2014, 14(6): 110-116 |
| [16] | 姚佼, 徐洁琼. 基于混合聚类的城市道路多时段控制研究[J]. 计算机应用研究, 2016, 33(11): 3274-3278 YAO Jiao, XU Jie-qiong. Mixed Clustering Based Time of Day Control Study in Urban Road[J]. Application Research of Computers, 2016, 33(11): 3274-3278 |
| [17] | COHEN D, HEAD L, SHELBY S. Performance Analysis of Coordinated Traffic Signals During Transition[J]. Transportation Research Record, 2007, 2035: 19-31 |
| [18] | LEE J, WILLIAMS B M. Development and Evaluation of a Constrained Optimization Model for Traffic Signal Plan Transition[J]. Transportation Research Part C:Emerging Technologies, 2009, 20(1): 185-198 |
| [19] | SHELBY S, BULLOCK D, GETTMAN D. Transition Methods in Traffic Signal Control[J]. Transportation Research Record, 2006, 1978: 130-140 |
| [20] | HUSCH D, ALBECK J. Synchro Studio 7 User Guide[M]. Sugar Land, US: Trafficware Ltd, 2006. |
| [21] | 茆诗松, 程依明, 濮晓龙, 等. 概率论与数理统计教程[M]. 2版. 北京: 高等教育出版社, 2011. MAO Shi-song, CHENG Yi-ming, PU Xiao-long, et al. Probability and Mathematical Statistics[M]. 2nd ed. Beijing: Higher Education Press, 2011. |
| [22] | 诸静. 模糊控制原理与应用[M]. 北京: 机械工业出版社, 1995. ZHU Jing. Fuzzy Control Theory and Application[M]. Beijing: China Machine Press, 1995. |
| [23] | 李士勇. 模糊控制[M]. 哈尔滨: 哈尔滨工业大学版社, 2011. LI Shi-yong. Fuzzy Control[M]. Harbin: Harbin Institute of Technology Press, 2011. |
| [24] | 张敏. 城市交通干线协调控制系统研究[D]. 广州: 华南理工大学, 2000. ZHANG Min. Research on Coordinated Control System of Urban Arterial[D]. Guangzhou:South China University of Technology, 2000. http://cdmd.cnki.com.cn/Article/CDMD-10216-1015901096.htm |
| [25] | 诸静. 模糊控制理论与系统原理[M]. 北京: 机械工业出版社, 2005. ZHU Jing. Fuzzy Control Theories and System Principle[M]. Beijing: China Machine Press, 2005. |
| [26] | 杨善林, 李永森, 胡笑旋, 等. K-means算法中的k值优化问题研究[J]. 系统工程理论与实践, 2006, 26(2): 97-101 YANG Shan-lin, LI Yong-sen, HU Xiao-xuan, et al. Optimization Study on k Value of K-means Algorithm[J]. Systems Engineering-Theory and Practice, 2006, 26(2): 97-101 |
| [27] | DUDOIT S, FRIDLYAND J. A Prediction-based Resampling Method for Estimating the Number of Clusters in a Dataset[J]. Genome Biology, 2002, 3(7): 129-137 |
| [28] | 王殿海, 严宝杰. 交通流理论[M]. 北京: 人民交通出版社, 2002. WANG Dian-hai, YAN Bao-jie. Traffic Flow Theory[M]. Beijing: China Communications Press, 2002. |
| [29] | SALTER R J. Highway Traffic Analysis and Design[M]. Washington, D.C.: ACMILIAN, 1989. |
| [30] | 肖晓伟, 肖迪, 林锦国, 等. 多目标优化问题的研究概述[J]. 计算机应用研究, 2011, 28(3): 805-809 XIAO Xiao-wei, XIAO Di, LIN Jin-guo, et al. Overview on Multi-objective Optimization Problem Research[J]. Application Research of Computers, 2011, 28(3): 805-809 |
| [31] | 雷德明, 严新平. 多目标智能优化算法及其应用[M]. 北京: 科学出版社, 2009. LEI De-ming, YAN Xin-ping. Multi Objective Intelligent Optimization Algorithm and Its Application[M]. Beijing: Science Press, 2009. |
| [32] | 蒋勇, 李宏, 焦永昌. 改进NSGA-Ⅱ终止判断准则[J]. 计算机仿真, 2009, 26(2): 196-200 JIANG Yong, LI Hong, JIAO Yong-chang. A New Termination Criterion of NSGA-Ⅱ[J]. Computer Simulation, 2009, 26(2): 196-200 |
 2017, Vol. 34
2017, Vol. 34
