扩展功能
文章信息
- 李祝龙, 李鹏飞, 梁养辉, 胡滨, 胡小兵
- LI Zhu-long, LI Peng-fei, LIANG Yang-hui, HU Bin, HU Xiao-bing
- 波纹钢管用作隧道逃生管道时的模拟分析
- Simulation Analysis of Corrugated Steel Pipe Used as Tunnel Escape Pipe
- 公路交通科技, 2017, 34(8): 105-113
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(8): 105-113
- 10.3969/j.issn.1002-0268.2017.08.015
-
文章历史
- 收稿日期: 2016-11-22
2. 中交第一公路勘察设计研究院有限公司, 陕西 西安 710064
2. CCCC First Highway Consultants Co., Ltd., Xi'an Shaanxi 710064, China
根据《公路隧道施工技术规范》中划分的围岩分级可知,Ⅲ、Ⅳ、Ⅴ级围岩必须使用隧道逃生装置[1]。根据美国矿山安全健康局有关隧道逃生通道研究资料显示,隧道施工的过程中会修建一些逃生装置,在逃生装置内放上食物、手电、呼吸器等,为隧道施工人员逃生提供帮助[2-3]。目前我国也开始研究隧道逃生管道,当面临“关门塌方”时,一方面施工作业人员可以进入逃生管道中躲避,可以有效防止二次伤害;另一方面,救援人员实施援救的过程中,可以通过敲击逃生管道判断隧道里面情况,而且当逃生管道变形不大的情况下,被困人员可以顺利从逃生管道中逃出[4]。
现在国内的隧道逃生管道一般采用直径为800 mm的圆钢管,管节长度为15 m,壁厚7 mm,管节间可采用直径大于逃生管道直径的套管连接。逃生管道在二衬台车移动就位过程中,临时拆移时应逐节拆除,逐节拆除、移动一般需要机械配合。由于设置逃生管道的繁琐性和机械配合及干扰施工等原因,加之管理措施不到位,许多隧道施工均未设置逃生管道[5-6]。针对上述分析,采用适应地形和变形、抗坍塌冲击、便于拆卸安装的拼装式波纹钢管逃生通道,其技术优点包括以下这3个方面:(1) 由于管道为波纹形,可以抵抗一定塌方体的冲击荷载,可以在一定斜坡时防止管道滑移,直径为1 000 mm的钢管壁厚可以降低至5 mm以下[7];(2) 采用片状管片拼装,不需要套管连接,不需要机械配合,1~2名工人可以完成拆卸、拼装及管道周转等工序,且效率高;(3) 片状管片便于储存、运输和周转使用,大大节约工程费用[8-9]。
我国在隧道逃生管道方面研究极少,经验十分缺乏,本文采用有限元软件建立波纹钢管和圆钢管模型,对坍塌岩石体垂直落在逃生管道上的情形进行动态模拟分析,通过分析不同管材不同条件下碰撞过程产生的应力变化和凹陷值,为隧道逃生管道方面的研究提供一定的参考。
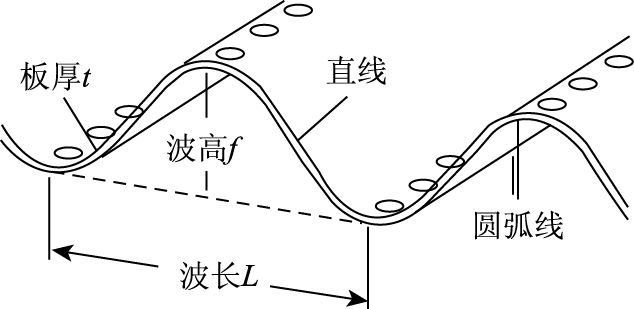
1 算例概况 1.1 模型基本信息使用有限元建立模型应具有代表性并且模型不宜过大[10],所建三维实体模型为有垫层波纹钢管和圆钢管模型两种,模型长度均为6 m,波纹钢管和圆钢管均选壁厚为5 mm和10 mm的两种,直径均为1 m,所采用波纹钢管材料参数为:波长×波高为150 mm×50 mm(见图 1),隧道一般塌方在500~1 000 m2,大塌方面积在1 000 m2以上[11-13],经换算简化模型,塌方体采用直径为0.8 m的球体垂直落下。
|
| 图 1 波形示意图 Fig. 1 Schematic diagram of waveform |
| |
1.2 单元选取
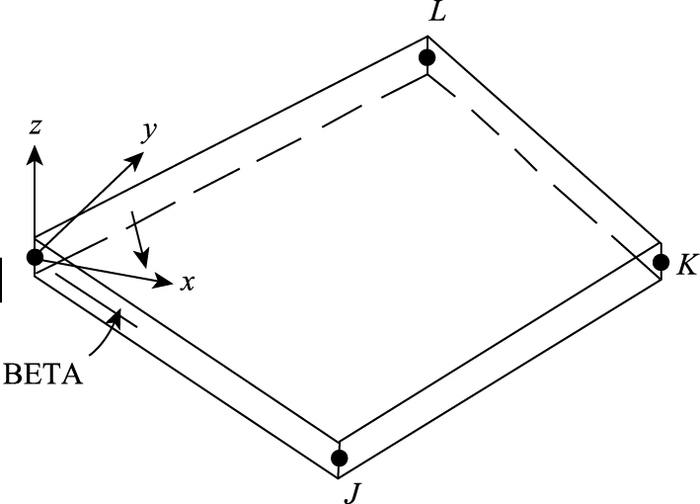
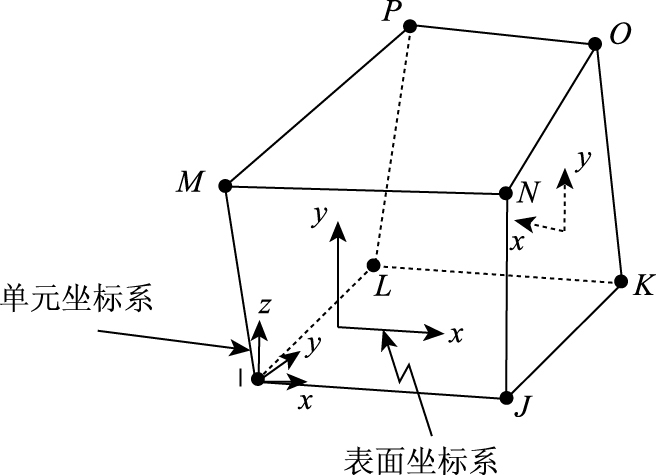
选取shell63四节点壳单元(shell63是既具有弯曲能力又具有膜力,可以承受平面内荷载和法向荷载,每个节点具有6个自由度,沿节点坐标系X, Y, Z方向的平动和沿节点坐标系X, Y, Z轴的转动的单元,如图 2所示)建立波纹钢管模型[14],选取solid45八节点实体单元(solid45是通过8个节点来定义,每个节点有3个沿着x,y,z方向平移的自由度的单元,如图 3所示)建立岩石体和垫层土体。采用积分法计算波纹钢管的截面特性参数:截面面积As=6.213 mm2/mm;截面转动惯量I=1 848.4 mm4/mm。波纹钢管、圆钢管、岩石体和垫层材料等相关参数按表 1设置。波纹钢管的单元形状取四边形,垫层单元取六面体,岩石单元取四面锥体,在允许计算的误差范围内,尽量减少单元数目,防止计算过于复杂。网格划分的顺序可以采用先划分波纹钢管单元,再划分岩石体及垫层土体单元。
|
| 图 2 shell63单元示意图 Fig. 2 Schematic diagram of Shell 63 unit |
| |
|
| 图 3 solid45单元示意图 Fig. 3 Schematic diagram of solid45 unit |
| |
| 材料 | 弹性模量/
MPa | 密度/
(kg·m-3) | 泊松比 | 切线模量/
GPa | 屈服强度/
MPa |
| 波纹钢管 | 210×103 | 7 850 | 0.3 | 6.1 | 235 |
| 圆管 | 210×103 | 7 850 | 0.3 | 2 | 200 |
| 岩石体 | 20 | 1 940 | 0.29 | 0.01 | 1 |
| 垫层土体 | 35 | 2 600 | 0.26 | 0.016 | 1 |
1.3 边界条件
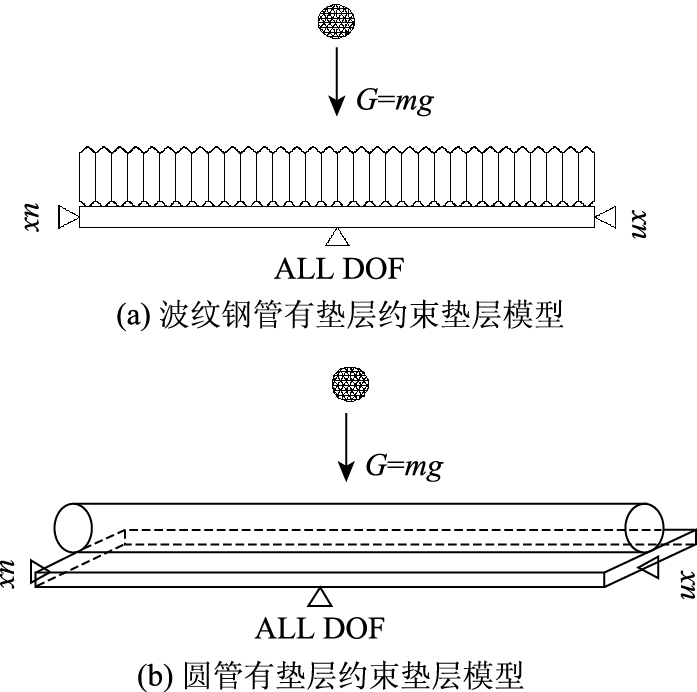
模型经过反复调节,以下约束条件为最靠近理论状况的合适条件:底面的水平和竖向位移以及扭转自由度施加ALL DOF约束(X,Y,Z 3个方向所有自由度全部约束),垫层土体施加水平位移约束ux,岩石采用自由落下无水平竖向约束(如图 4所示)。
|
| 图 4 边界条件施加示意图 Fig. 4 Schematic diagrams of boundary condition |
| |
1.4 基本假定
本文主要研究荷载对象为塌方岩石体,在对隧道逃生波纹钢管进行动态有限元模拟计算过程中,隧道塌方岩石为自由落体,塌方体简化为球体,无任何约束。
本文在全局坐标系下进行建立三维实体模型,坐标轴按照笛卡尔坐标系,有如下假定:
(1) 大断面隧道施工过程中造成的垮塌面近似认为岩石球体自由落体砸下;
(2) 按照国内隧道设计标准《公路隧道设计规范》(JTG D70—2004) 和《公路隧道设计细则》(JTG/T D70—2010),按照双孔隧道,采用直角边墙净空高度为6.17 m,仰拱厚度40~65 cm[15-16],考虑隧道塌方体从距波纹钢管顶7 m高处垂直落下[17];
(3) 假定岩石在砸向波纹钢管的过程中,不发生水平位移,前后不滑左右不滚,能量完全都被波纹钢管吸收;
(4) 假定岩石在撞击波纹钢管的过程中,波纹钢管的竖向位移与垫层土体一致。
2 不同厚度波纹钢管撞击有限元结果分析利用动态有限元分析软件对冲击试验进行三维仿真模拟分析,仿真模型由以下部分构成:落石、波纹钢管以及垫层,其中落石和垫层采用六面体八节点实体单元,波纹钢管采用壳单元壁厚分别为5 mm和10 mm。在有限元中定义材料的属性参数见表 1。在动态有限元模拟分析模型中设置落石碰撞波纹钢管的作用时间为0.2 s,时间步数100,岩石共划分2 048个八节点实体单元,波纹钢管共划分8 424个四节点壳体单元,垫层共划分1 600个八节点实体单元。
隧道顶部岩石块体自由落下时,速度可由能量守恒公式确定:
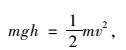
|
(1) |
式中,m为岩石质量;g为重力加速度;h为落石下落高度;v为落石碰撞结构物时的瞬间速度。
通过上述公式(1) 可以将模型进行简化,我们采用落石从隧道洞顶自由下落高度为7 m,落石撞击波纹钢管的速度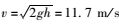
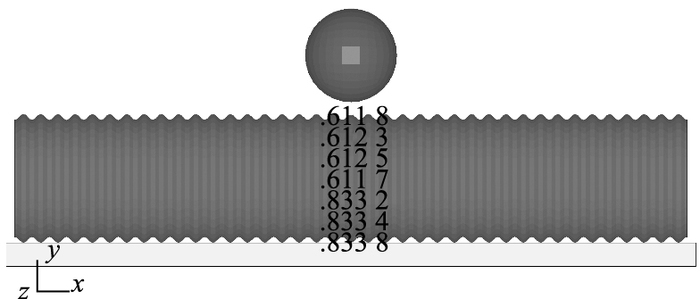
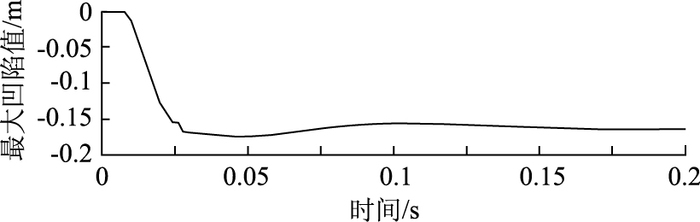
波纹钢管Y方向上提取点位置如图 5所示,对应断面位置如图 6所示。波纹钢管厚度分别为5 mm和10 mm,对其分别研究。图 7和图 8给出了中间断面作用3.56×104 J能量时最大凹陷点的时程曲线,冲击过程后半部分主要为波纹钢管的弹性恢复部分。从有限元后处理模拟图中可以看出冲击过程结束后,波纹钢管产生振动,这与实际工程中的波纹钢管的振动现象吻合。
|
| 图 5 波纹钢管Y方向上提取点位置图 Fig. 5 Positions of extraction points in Y direction of corrugated steel pipe |
| |
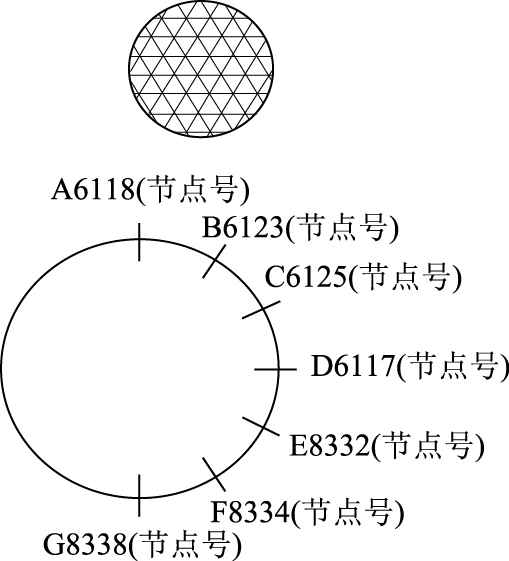
|
| 图 6 波纹钢管Y方向上断面提取点位置图 Fig. 6 Positions of cross-section extraction points in Y direction of corrugated steel pipe |
| |
|
| 图 7 壁厚为5 mm的波纹钢管Y方向最大凹陷变形的时程曲线 Fig. 7 Time history curve of maximum depression in Y direction of corrugated steel pipe with wall thickness of 5 mm |
| |
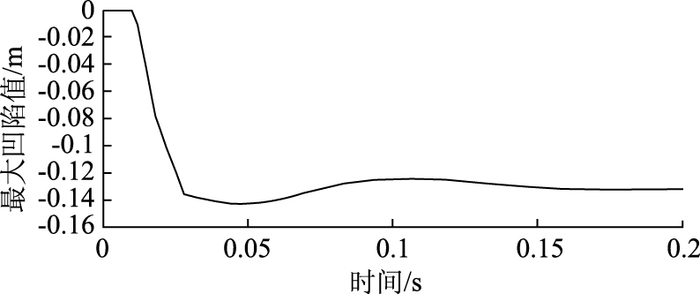
|
| 图 8 壁厚为10 mm的波纹钢管Y方向最大凹陷变形的时程曲线 Fig. 8 Time history curve of maximum depression in Y direction of corrugated steel pipe with wall thickness of 10 mm |
| |
由图 7和图 8分析知:岩石垂直砸向波纹钢管的冲击时间都为8 ms,岩石和波纹钢管撞击接触的时间都约为15 ms,此段接触过程为能量的转换过程,岩石的重力势能转化为钢材的内能,从而使波纹钢管发生凹陷变形,壁厚较厚的波纹钢管承受岩石撞击变形的抵抗力较好,波纹管出现最大凹陷变形之后会出现部分弹性恢复部分,且此部分恢复变形较小。管壁较厚的变形较小,符合撞击规律。由图 9分析知,厚度为5 mm的波纹钢管Y方向上的最大凹陷值为174 mm,厚度为10 mm的波纹钢管Y方向上的最大凹陷值为143 mm,沿着Y方向继续向下,凹陷变形越来越小,凹陷值的变化出现细微的波动。这种变化与钢的材料性质有关(刚度越大,凹陷值的恢复能力越小;韧性越大,凹陷值恢复能力越大)。
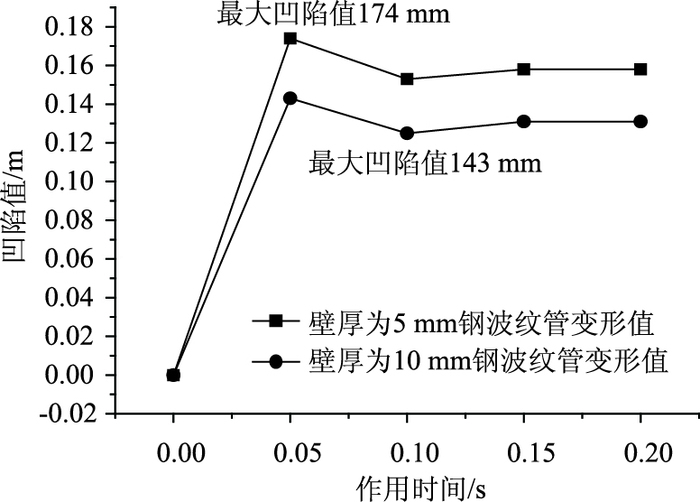
|
| 图 9 波纹钢管不同壁厚凹陷值与撞击时间关系曲线 Fig. 9 Curves of depression vs. impact time of corrugated steel pipe with different wall thicknesses |
| |
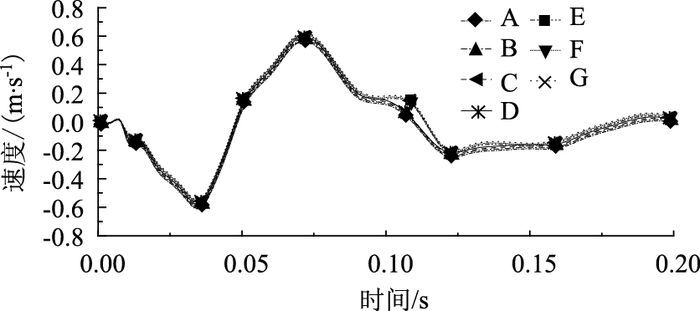
由图 10和图 11所知:波纹钢管在受到岩石的撞击过程中,撞击点下方的速度-时间曲线变化规律基本一致;从波动图中可以看出,随着时间的延长波峰波谷越来越平缓,渐渐速度趋于零,说明波纹钢管在受到冲击的过程中,动能转换成内能,部分内能在转换成动能,最终速度变为零。
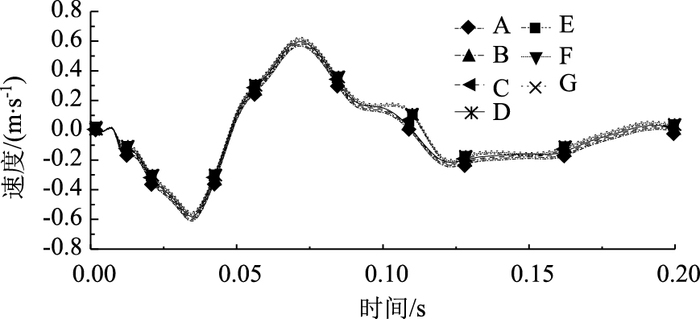
|
| 图 10 壁厚为5 mm的波纹钢管Y方向上所取点的速度-时间曲线 Fig. 10 Velocity-time curve in Y direction of corrugated steel pipe with wall thickness of 5 mm |
| |
|
| 图 11 壁厚为10 mm的波纹钢管Y方向上速度-时间曲线 Fig. 11 Velocity-time curve in Y direction of corrugated steel pipe with wall thickness of 10 mm |
| |
2.2 波纹钢管X方向上凹陷变形情况
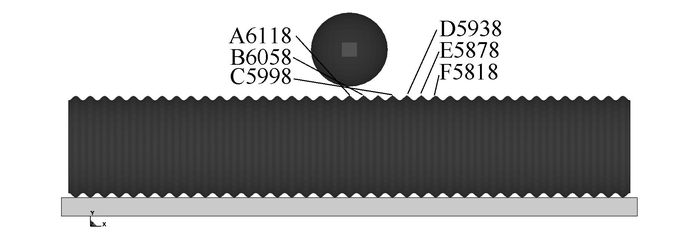
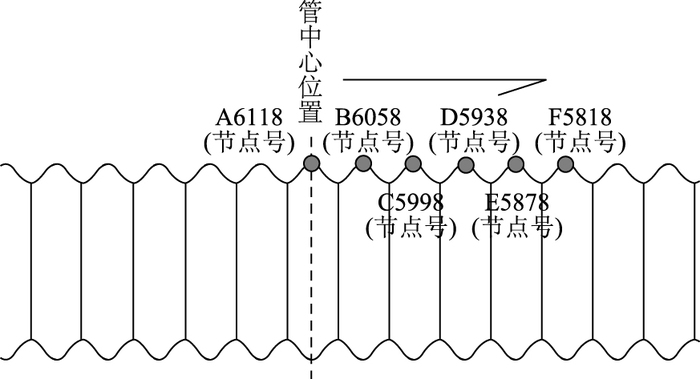
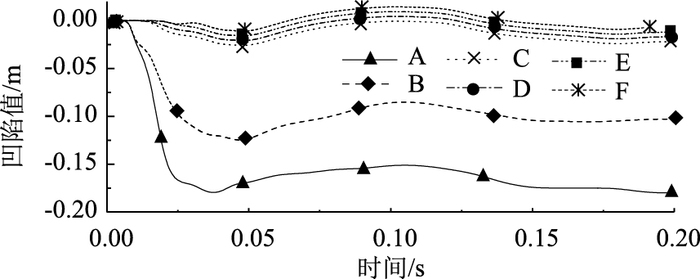
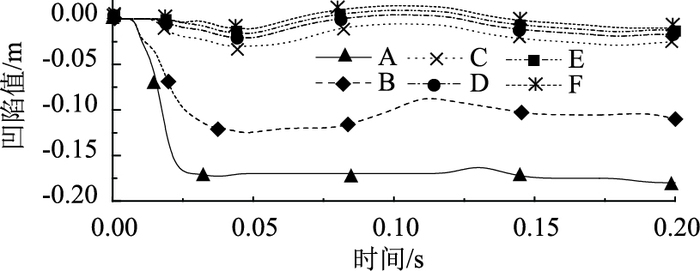
波纹钢管X方向上提取点位置如12所示,对应断面位置如图 13所示。从图 14可知:波纹钢管X方向的最大值凹陷值出现在岩石的垂直方向上,最大凹陷值为174 mm,X方向上第二波峰上去的点的凹陷值为117 mm,随着距离最大凹陷值越远的部分,凹陷值渐渐趋于零,且出现波动现象。从图 15可知:波纹钢管X方向的最大值凹陷值出现在岩石的垂直方向上,最大凹陷值为143 mm,X方向上第二波峰上去的点的凹陷值为110 mm,随着距离最大凹陷值越远的部分,凹陷值渐渐趋于零,且出现波动现象。
|
| 图 12 波纹钢管X方向上提取点位置图 Fig. 12 Positions of extraction points in X direction of corrugated steel pipe |
| |
|
| 图 13 波纹钢管X方向上断面取点位置图 Fig. 13 Positions of cross-section extraction points in X direction of corrugated steel pipe |
| |
|
| 图 14 壁厚为5 mm的波纹钢管X方向上凹陷变形的时程曲线 Fig. 14 Time history curve of depression in X direction of corrugated steel pipe with wall thickness of 5 mm |
| |
|
| 图 15 壁厚为10 mm的波纹钢管X方向上凹陷变形的时程曲线 Fig. 15 Time history curve of depression in X direction of corrugated steel pipe with wall thickness of 10 mm |
| |
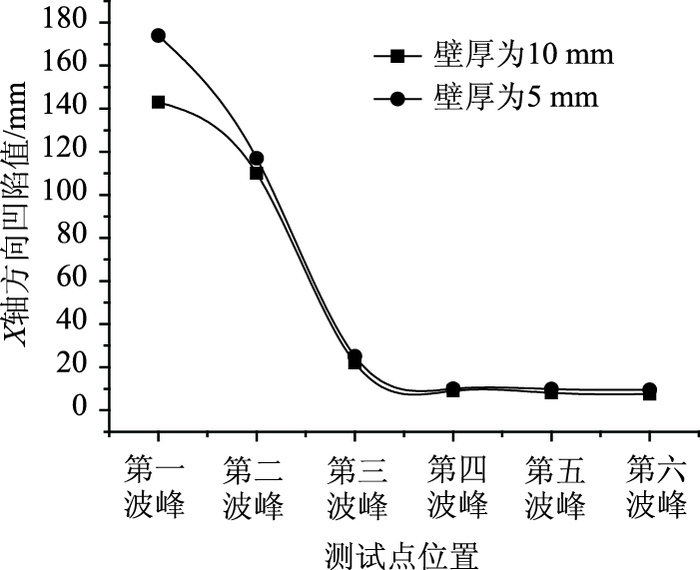
由图 16分析知,随着离撞击点位置越来越远,出现的凹陷值的变化会越来越小,最后趋于稳定;从分析图上可以看出,凹陷值变化最大的部分即为波纹钢管受到撞击的部位,随之凹陷值变化会急剧减小,但是会慢慢减为零,这也符合钢材的材料特性,在撞击的位置出现塑性变形,远离撞击点的位置,由于还在弹性阶段会慢慢恢复变形。
|
| 图 16 不同位置凹陷变形对比分析图 Fig. 16 Comparison of depressions at different positions |
| |
2.3 波纹钢管加速度变化情况
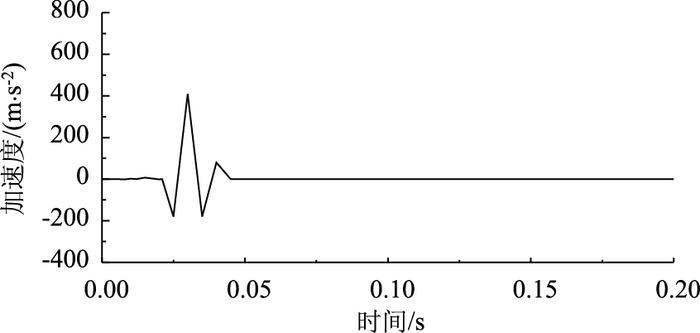
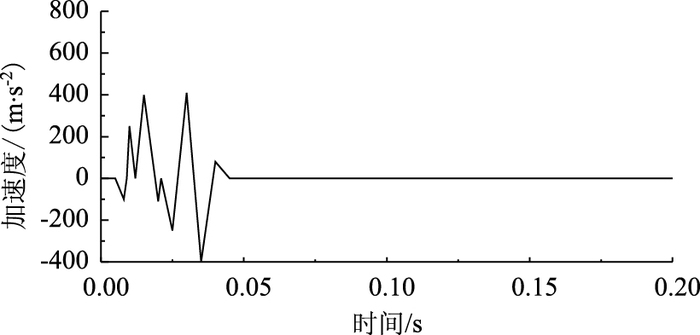
由图 17和图 18可知:壁厚为5 mm和10 mm的波纹钢管在受到岩石的撞击过程中,只有撞击过程才产生加速度的变化,岩石在与波纹钢管碰撞之前以及作用力之后加速度基本为零,且作用时间与凹陷变形的时间一致;但是厚度为5 mm的波纹钢管加速度最大绝对值比厚度为10 mm的大,说明较厚的波纹钢管能够更好地抵抗岩石体对管道的撞击,管道的变形较小。
|
| 图 17 壁厚为5 mm的波纹钢管各点的加速度变化曲线 Fig. 17 Acceleration curves of corrugated steel pipe with wall thickness of 5 mm |
| |
|
| 图 18 壁厚为10 mm各点的加速度变化曲线 Fig. 18 Acceleration curves of corrugated steel pipe with wall thickness of 10 mm |
| |
3 不同厚度有垫层圆管撞击有限元分析
岩石和垫层采用采用六面体八节点实体单元,圆管采用四节点壳体单元,壁厚分别取5和10 mm,在有限元中定义材料的属性参数见表 1。模型采用碰撞作用时间为1 s,时间步数100,岩石共划分864个八节点实体单元,圆管共划分270个四节点壳体单元,垫层共划分1 064个八节点实体单元。岩石为球体,直径为0.8 m,质量为520 kg,球体竖向距离圆管7 m,球砸向圆管的速度为11.7 m/s.
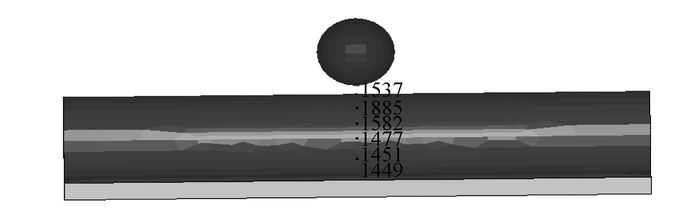
3.1 圆管Y方向上凹陷变形情况圆管Y方向上提取点位置如图 19所示,对应的断面位置如图 20所示。分别研究圆管厚度分别为5 mm和10 mm。图 21和图 22给出了中间断面作用3.56×104 J能量时最大凹陷点的时程曲线,冲击过程后半部分主要为波纹钢管的弹性恢复部分。从有限元后处理模拟图中可以看出冲击过程结束后,圆管产生振动,这与现场观察到的圆管的振动现象吻合。
|
| 图 19 圆管Y方向上提取点位置图 Fig. 19 Positions of extraction points in Y direction of round steel pipe |
| |
|
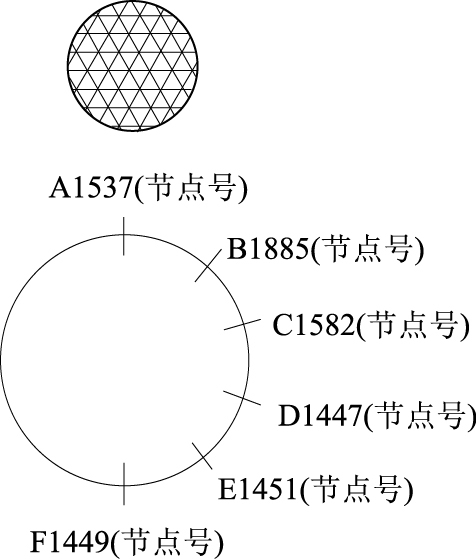
| 图 20 圆管Y方向上断面提取点位置图 Fig. 20 Positions of cross-section extraction points in Y direction of round steel pipe |
| |
|
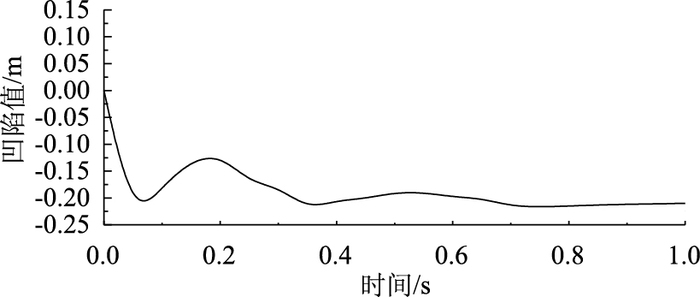
| 图 21 壁厚为5 mm的圆管Y方向最大凹陷变形的时程曲线 Fig. 21 Time history curve of maximum depression in Y direction of round steel pipe with wall thickness of 5 mm |
| |
|
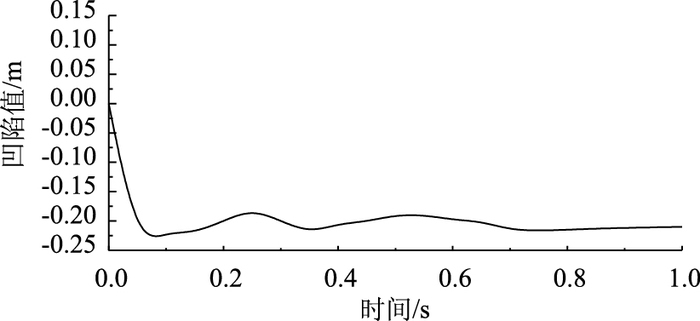
| 图 22 壁厚为10 mm的圆管Y方向最大凹陷变形的时程曲线 Fig. 22 Time history curve of maximum depression in Y direction of round steel pipe with wall thickness of 10 mm |
| |
从图 21和图 22对比分析可知:壁厚为5 mm圆管最大变形为214 mm,壁厚为10 mm圆管最大变形为199 mm,壁厚越厚最大变形值小,结构更偏于安全。
由图 21和图 22得出相同规律:岩石砸向圆管的冲击时间都约为8 ms,岩石和圆管撞击接触的时间都约为15 ms,此段接触过程为能量的转换过程,岩石的重力势能转化为钢材的内能,从而使圆管发生凹陷变形,壁厚较厚的圆管承受岩石撞击变形的抵抗力较好,波纹管出现最大凹陷变形之后会出现部分弹性恢复部分,且此部分恢复变形较小。
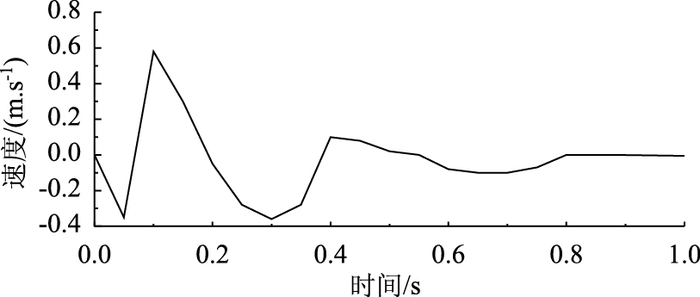
由图 23和图 24对比分析知:圆管在受到岩石的撞击过程中,撞击点下方的速度-时间曲线变化规律基本一致,从波动图中可以看出,随着时间的延长波峰波谷越来越平缓,渐渐速度趋于零,说明波纹钢管在受到冲击的过程中,动能转换成内能,部分内能在转换成动能,最终速度变为零。
|
| 图 23 壁厚为5 mm的圆管Y方向上所取点的速度-时间曲线 Fig. 23 Velocity-time curve in Y direction of round steel pipe with wall thickness of 5 mm |
| |
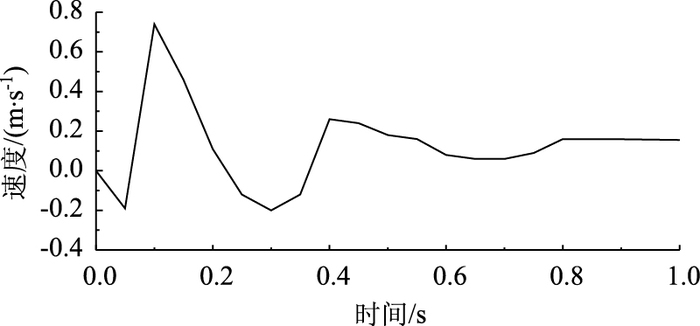
|
| 图 24 壁厚为10 mm的圆管Y方向上速度-时间变化曲线 Fig. 24 Velocity-time curve in Y direction of round steel pipe with wall thickness of 10 mm |
| |
3.2 圆管X方向上凹陷变形情况
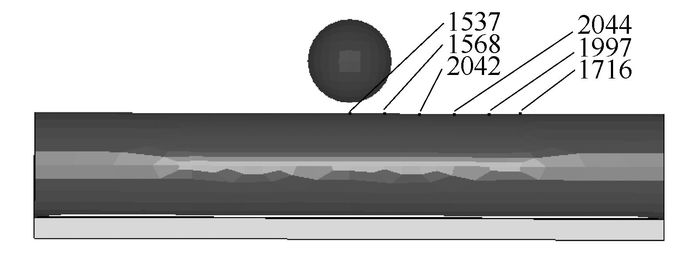
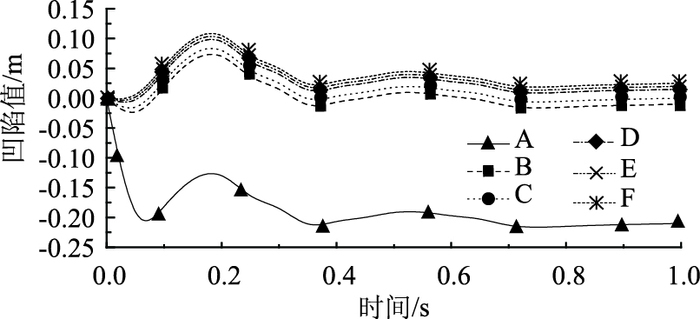
圆管X方向上提取点位置如图 25所示,对应断面位置如图 26所示。从图 27可知:圆管X方向的最大值凹陷值出现在岩石的垂直方向上,最大凹陷值为221 mm,随着距离最大凹陷值越远的部分,凹陷值渐渐趋于零,且出现波动现象,随着时间的延长,凹陷值的变化最后曲线趋于直线。
|
| 图 25 圆管X方向上提取点位置图 Fig. 25 Positions of extraction points in X direction of round steel pipe |
| |
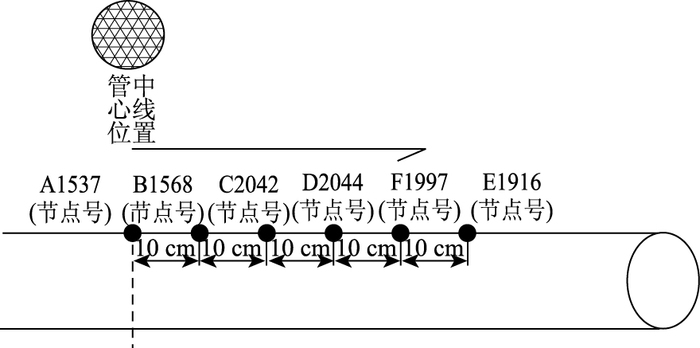
|
| 图 26 圆管X方向上断面提取点对应位置图 Fig. 26 Positions of cross-section extraction points in X direction of round steel pipe |
| |
|
| 图 27 壁厚为5 mm的圆管X方向上凹陷值变化的时程曲线 Fig. 27 Time history curve of depression in X direction of round steel pipe with wall thickness of 5 mm |
| |
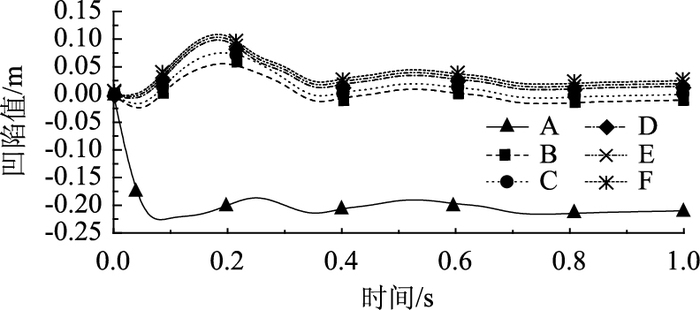
从图 28可知:圆管X方向的最大值凹陷值出现在岩石的垂直方向上,最大凹陷值为200 mm,随着距离最大凹陷值越远的部分,凹陷值渐渐趋于零,且出现波动现象,凹陷值变化最后趋于直线。
|
| 图 28 壁厚为10 mm的圆管X方向上凹陷值变化的时程曲线 Fig. 28 Time history curve of depression in X direction of round steel pipe with wall thickness of 10 mm |
| |
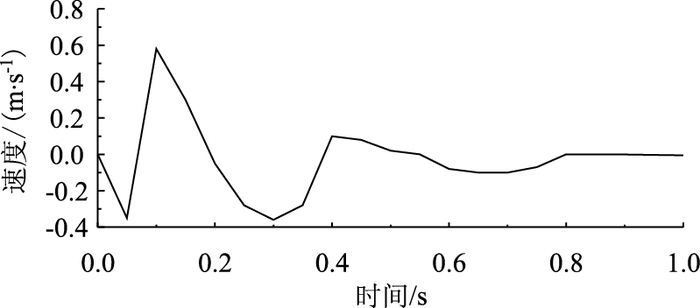
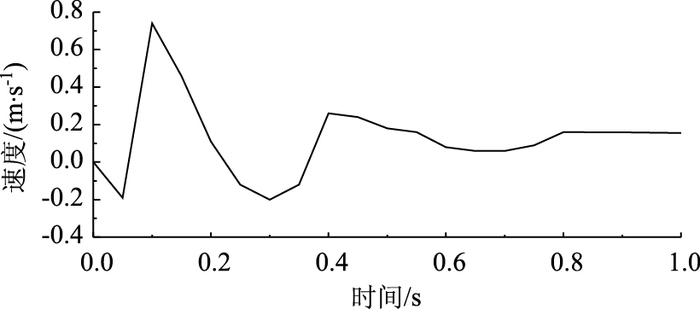
由图 29和图 30对比分析知:圆管在受到岩石的撞击过程中,撞击点下方的速度-时间曲线变化规律基本一致,从波动图中可以看出,随着时间的延长波峰波谷越来越平缓,渐渐速度趋于零,说明圆管在受到冲击的过程中,动能转换成内能,部分内能在转换成动能,最终速度变为零。
|
| 图 29 壁厚为5 mm的圆管X方向上所取点的速度-时间变化曲线 Fig. 29 Velocity-time curve in X direction of round steel pipe with wall thickness of 5 mm |
| |
|
| 图 30 壁厚为10 mm的圆管X方向上所取点的速度-时间变化曲线 Fig. 30 Velocity-time curve in X direction of round steel pipe with wall thickness of 10 mm |
| |
3.3 圆管加速度变化情况
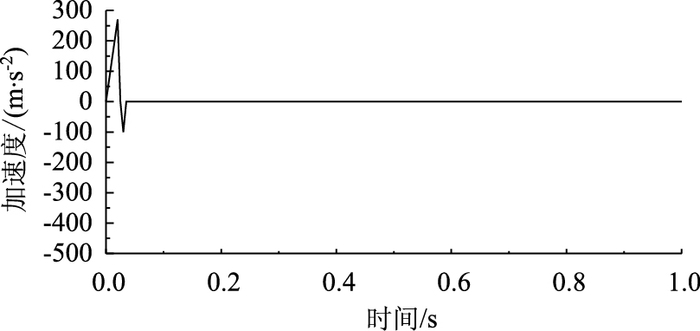
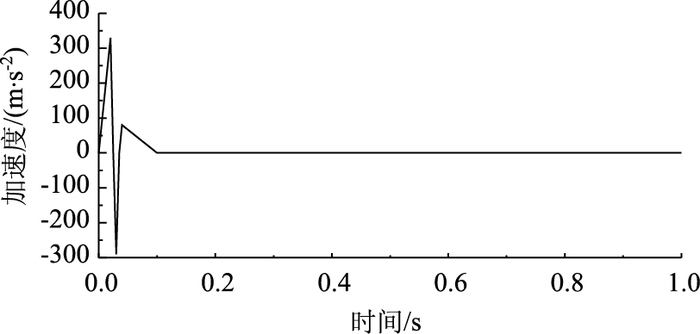
由图 31和图 32可知:壁厚为5和10 mm的圆管在受到岩石的撞击过程中,只有撞击过程才产生加速度的变化,岩石在与圆钢管碰撞之前以及作用力之后加速度基本为零,且作用时间与凹陷变形的时间一致。与图 17和图 18相比,相同厚度的圆管比波纹钢管作用时间较短,说明岩石对圆管作用较为集中短暂,波纹钢管能够更好地分散猛烈的撞击;圆管比波纹钢管产生加速度的时间早,说明圆管遇到撞击后更易变形。
|
| 图 31 壁厚为5 mm的圆管各点的加速度变化曲线 Fig. 31 Acceleration curve of round steel pipe with wall thickness of 5 mm |
| |
|
| 图 32 壁厚为10 mm各点的加速度变化曲线 Fig. 32 Acceleration curve of round steel pipe with wall thickness of 10 mm |
| |
4 结论
(1) 结合当前我国现场施工情况,模拟逃生管道受到岩石撞击,变形规律符合施工现场情况,说明依靠有限元软件进行实体建模分析、预测是可行的。
(2) 目前隧道逃生管道较多采用直径80 cm的圆管,壁厚6~8 mm,结合国内隧道塌方,通过动态有限元模拟圆管在受到撞击的过程中产生的凹陷变形,比较波纹钢管在受到岩石撞击的过程中所产生的凹陷变形,得出直径1 m,壁厚为5 mm和壁厚10 mm的波纹钢管凹陷变形分别为174 mm和143 mm,直径1 m,壁厚为5 mm和壁厚10 mm圆管最大变形分别为214 mm和199 mm,波纹钢管凹陷变形较圆管分别小40 mm和56 mm,相同管径下,随着壁厚的增加,波纹钢管的优势就越明显。
(3) 波纹钢管和圆管在受到岩石的撞击过程中,速度-时间变化曲线规律一致,说明钢材受到冲击产生变形过程中能量的转化速度基本一致,由速度-时间变化曲线图可知,波纹钢管在受到岩石的撞击过程中,可以避免峰值过大而且结构更加稳定。
(4) 在受到撞击时波纹钢管相对圆钢管变形虽然较小,安装和移动较方便,但是也存在波纹管比圆钢管造价要高的问题,例如通过减小其壁厚或加入合金材料但抵抗变形的能力不变等方法来降低造价的问题是值得继续探究的。
| [1] | JTG F60-2009, 公路隧道施工技术规范[S]. JTG F60-2009, Technical Specifications for Construction of Highway Tunnel[S]. |
| [2] | 邹文斌. 公路隧道施工围岩安全信息监控与预警研究[D]. 长沙: 中南大学, 2010. ZOU Wen-bin. Monitoring and Early Warning of Rock Security Information for Highway Tunnel Construction[D].Changsha:Central China University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10533-2010188958.htm |
| [3] | HUNGR O, MORGAN G C, KELLERHALS R. Quantitative Analysis of Debris Torrent Hazards for Design of Remedial[J]. Canadian Geotechnical Journal, 2011, 21(4): 663-677 |
| [4] | 张臻. 公路隧道逃生方案研究[D]. 西安: 长安大学, 2009. ZHANG Zhen. Study on Highway Tunnel Escape Plan[D]. Xi'an:Chang'an University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-11941-2009210029.htm |
| [5] | 杨飚, 庄富盛. 新型隧道逃生管道设计模拟及现场试验研究[J]. 公路交通技术, 2013(2): 111-114 YANG Biao, ZHUANG Fu-sheng. Simulation and On-site Experimental Research of New Escape Pipeline Design in Tunnels[J]. Technology of Highway and Transport, 2013(2): 111-114 |
| [6] | 张浩. 隧道安全防护措施探讨[J]. 铁道工程学报, 2009, 127(4): 35-38 ZHANG Hao. Exploration on the Security Measure for Railway Tunnel[J]. Journal of Railway Engineering Society, 2009, 127(4): 35-38 |
| [7] | 陈伟健, 汪永兰. 公路波纹钢管涵洞设计计算[J]. 交通标准化, 2014, 42(23): 95-100 CHEN Wei-jian, WANG Yong-lan. Design and Calculation of Highway Corrugated Steel Pipe Culverts[J]. Transportation Standardization, 2014, 42(23): 95-100 |
| [8] | 李祝龙. 公路波纹钢管涵洞设计与施工技术[M]. 北京: 人民交通出版社, 2007. LI Zhu-long. Highway Corrugated Steel Pipe Culvert Design and Construction Technology[M]. Beijing: China Communications Press, 2007. |
| [9] | 刘成志. 钢波纹管涵洞在公路建设中应用技术分析[J]. 公路交通技术, 2009(4): 103-105 LIU Cheng-zhi. Technical Analysis of Application of Corrugated Steel Tube Culvert in Highway Construction[J]. Technology of Highway and Transport, 2009(4): 103-105 |
| [10] | 何思明, 沈均, 吴永. 滚石冲击荷载下棚洞结构动力响应[J]. 岩土力学, 2011, 32(3): 781-788 HE Si-ming, SHEN Jun, WU Yong. Rock Shed Dynamic Response to Impact of Rock-fall[J]. Rock and Soil Mechanics, 2011, 32(3): 781-788 |
| [11] | 王艳丽, 李祝龙, 吴大中. 钢波纹管涵洞的薄壳效应[J]. 公路交通科技, 2008, 25(5): 86-90 WANG Yan-li, LI Zhu-long, WU Da-zhong. Thin Shell Effect of Corrugated Steel Culvert Performance[J]. Journal of Highway and Transportation Research and Development, 2008, 25(5): 86-90 |
| [12] | BEBEN D. Corrugated Steel Plate Culvert Response to Service Train Loads[J]. Journal of Performance of Constructed Facilities, 2012, 28(2): 376-390 |
| [13] | 杨明辉, 方天云, 赵明华, 等. 高填方段波纹管涵垂直土压力试验及计算[J]. 公路交通科技, 2014, 31(4): 33-38 YANG Ming-hui, FANG Tian-yun, ZHAO Ming-hua, et al. Test and Calculation of Vertical Earth Pressure on Corrugated Pipe Culvert under High Embankment[J]. Journal of Highway and Transportation Research and Development, 2014, 31(4): 33-38 |
| [14] | 李祝龙, 刘百来, 李自武. 钢波纹管涵洞力学性能现场试验研究[J]. 公路交通科技, 2006, 23(3): 79-82 LI Zhu-long, LIU Bai-lai, LI Zi-wu. Field Mechanical Performance Test of Corrugated Steel Culvert[J]. Journal of Highway and Transportation Research and Development, 2006, 23(3): 79-82 |
| [15] | 张善元, 路国运, 程国强, 等. 圆管及内充压力介质管道撞击大变形与破坏[J]. 力学进展, 2004, 34(1): 23-31 ZHANG Shan-yuan, LU Guo-yun, CHENG Guo-qiang, et al. The Advances of Research on the Impact Damage and Failure of Empty and Half-filled Tubes[J]. Advances in Mechanics, 2004, 34(1): 23-31 |
| [16] | 胡浩军, 狄先均, 李家泰, 等. 隧道逃生管道设计中的圆管冲击计算[J]. 现代隧道技术, 2008(增1): 272-274 HU Hao-jun, DI Xian-jun, LI Jia-tai, et al. Pipe Shock Calculations in Tunnel Escape Piping Design[J]. Modern Tunnel Technology, 2008(S1): 272-274 |
| [17] | 张瑜, 丁庆荣, 狄先均, 等. 隧道逃生管道的冲击实验与仿真模拟[J]. 华中科技大学学报:城市科学版, 2010, 27(2): 87-89 ZHANG Yu, DING Qing-rong, DI Xian-jun, et al. Impact Experiment and Computer Simulation of Tube for Design of Escape Passage in Tunnel Construction[J]. Journal of Huazhong University of Science and Technology:Urban Science Edition, 2010, 27(2): 87-89 |
 2017, Vol. 34
2017, Vol. 34
