扩展功能
文章信息
- 金佳旭, 许彬, 董天文, 郎俊彪
- JIN Jia-xu, XU Bin, DONG Tian-wen, LANG Jun-biao
- 路桥结合部位水毁破坏规律研究
- Study on Flood Damage Rule of Road-bridge Binding Site
- 公路交通科技, 2017, 34(8): 98-104
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(8): 98-104
- 10.3969/j.issn.1002-0268.2017.08.014
-
文章历史
- 收稿日期: 2016-12-19
2. 东北大学 资源与土木工程学院, 辽宁 沈阳 110006
2. School of Resources and Civil Engineering, Northeastern University, Shenyang Liaoning 110006, China
“水毁”,即指因暴雨、洪水造成路基、路面、桥涵及其他设施的损毁。每年都有公路水毁现象的发生,轻者路基路面损坏而影响公路通行能力,重者桥梁冲毁致使交通中断,由此造成的损失相当严重,引起了社会各界的广泛关注。刘伟军[1]主要针对公路水毁的成因和治理措施作出了简要阐述;罗青等[2]基于国内外研究现状,从路基水毁特征和水毁类型出发,建立了边坡的有限元分析模型,研究发现,高速公路的边坡失稳主要出现在沟谷沿河路段,以及跨河大桥的桥头处;高永明等[3]基于公路路基水毁相关研究资料和野外现场调查结果,考虑水毁承载体和破坏机理,从边坡防护和路基排水两个角度,提出了公路路基水毁的防治对策;王继宏[4]详细阐述了各类水毁发生的原因以及对各类水毁的防治措施,指出公路水毁要以预防为主;胡建刚等[5]对公路的水毁破坏形式进行了分析归纳,结合路基工程类型和工程实例,提出了防治对策;马保成[6]提出了沿河公路、小桥涵和沟谷泥石流水毁易发地段的超前识别判据及路线危险性分段方法,实现了路线沿河公路水毁灾害的预判并建立了沿河公路水毁灾害危险度计算方法;国内众多研究者对我国山区公路工程水毁灾害[7-10]的研究成果丰富了水毁破坏治理理论[11-13]。此外,国外诸多学者针对公路工程水毁问题,做出了大量的研究并取得了一定成就[14-20]。
目前,有关路桥结合部位水毁破坏规律的研究涉及较少。公路工程水毁具有鲜明的区域性特点,有针对性地对辽宁区域某路桥结合部位水毁破坏进行实地考察,采用正交设计方法设计模型试验,并结合ADINA有限元数值计算,对多因素条件下水毁破坏规律进行研究分析,进一步揭示水毁破坏规律。
1 路桥结合部位水毁破坏模型试验 1.1 相似比确定模型试验是岩土工程的主要研究方法之一,其中,各物理参数相似比的确定可以使原型的物理规律在模型上得到正确的反映。流体运动中,原型和模型之间需要满足几何相似、运动相似、动力相似。本模型试验综合考虑制作模型的费用和难易程度、试验周期、数据测量的精确程度以及试验设备等条件,并经过相似性分析,最终确定模型试验的几何相似常数为Cl=25,且主要控制模型几何相似和运动相似,而运动相似中主要考虑流体流速相似。以Fr相似准则为基础推导出流体流速相似比,按公式(1) 计算得流体流速相似常数为Cv=5。于是,本模型试验几何相似比和流体流速相似比分别为25和5。
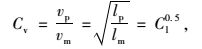
|
(1) |
式中, Cv为流体流速相似常数;vp和vm分别为流体原型和模型的流速;lp和lm分别为流体原型与模型的几何尺寸;Cl为模型几何相似常数。
根据辽宁区域某河段调查实测水文资料,结合上述相似比,得原型和模型有关参数见表 1所示。
| 流体流速/(cm·s-1) | 桥台高度/cm | ||
| 枯水水位 | 洪水水位 | ||
| 原型 | 119.0~208.0 | 50.0~68.0 | 500 |
| 模型 | 23.8~41.6 | 10.0~13.6 | 20 |
模型试验中结构体迎水面水流流速不应小于枯水水位流速最小值10.0 cm/s,且最大流速不应小于洪水水位流速最大值41.6 cm/s。根据模型试验结构体迎水面流速测试仪显示,迎水面水流流速介于43.0~68.0 cm/s之间,符合模型试验相似准则。
1.2 试验设备及工况本模型试验采用自行设计研发的公路桥台水毁模型试验系统装置,该系统主要包括槽体、水位控制系统、水流循环系统、动力系统和流速测试仪。试验中,为控制水槽中的水位高度,在水槽前后分别设置有通过水位控制系统控制的水闸,为了减小回流,出水口设置成60°斜向的水闸;水流循环系统是将由出水口流出槽体的水通过水泵运送方式重新运输到槽体的进水口;动力系统提供闸门高度和坡角等影响因素的变化情况。如此,此套试验装置系统通过一键式按钮的方法对不同工况进行模拟。
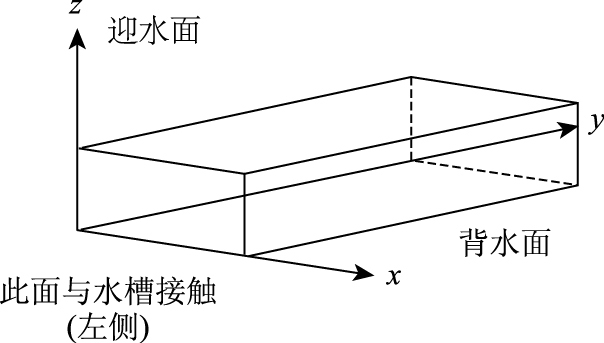
根据正交试验设计方法,本模型试验拟采用8种工况,以控制桥台伸入流体长度、倾角、坡比及防护技术,为了便于观测和阐述试验现象,建立模型三维坐标系,见图 1所示。分析各种因素影响下桥台水毁破坏的规律,各工况详见表 2。
|
| 图 1 模型坐标系 Fig. 1 Coordinate system of model |
| |
| 工况 | 模型长度/cm | 模型高度/cm | 水位/cm | 模型倾角/
(°) | 模型端头形状 | 流体进口位置 流速/(cm·s-1) | 冲刷时 间/s | 防护技术 | 坡比 |
| 1# | 20 | 20 | 15 | 90 | 矩形 | 80.0 | 900 | 无 | 0 |
| 2# | 40 | 20 | 15 | 90 | 矩形 | 80.0 | 900 | 无 | 0 |
| 3# | 60 | 20 | 15 | 90 | 矩形 | 80.0 | 900 | 无 | 0 |
| 4# | 40 | 20 | 15 | 45 | 矩形 | 80.0 | 900 | 无 | 0 |
| 5# | 40 | 20 | 15 | 135 | 矩形 | 80.0 | 900 | 无 | 0 |
| 6# | 40 | 20 | 15 | 90 | 矩形 | 80.0 | 900 | 无 | 1:1.5 |
| 7# | 40 | 20 | 15 | 90 | 矩形 | 80.0 | 900 | 注浆层 | 0 |
| 8# | 40 | 20 | 15 | 90 | 矩形 | 80.0 | 900 | 围堰 | 0 |
1.3 试验结果与分析
通过模型试验,对不同工况条件下所获得的试验结果进行分析,以揭示路桥结合部位水毁破坏规律。
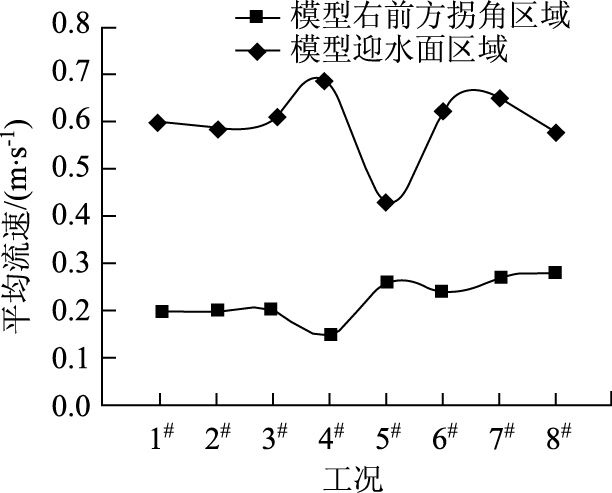
在模型迎水面和模型右前方拐角区域内任意坐标处测定水流速度,分别各测3次,各自取平均值,可得关系曲线图,详见图 2所示。
|
| 图 2 工况1#~8#条件下模型迎水面和模型右侧拐角区域水流平均流速关系曲线 Fig. 2 Average velocity relation curves of water flow about regions of surface and right corner of model under working conditions of 1#~8# |
| |
结合表 2和图 2分析可知:由于水流运行过程中存在能量损失,水流流速从流体进口位置至模型迎水面各区域过程中,流速均有所减小;工况1#~3#条件下,模型迎水面各区域的平均流速基本保持一致;而工况4#和5#条件下,其平均流速发生了显著变化,且模型前方迎水面和模型右前方拐角区域的平均流速大小呈反向趋势;工况6#~8#条件下,其平均流速变化情况亦较为稳定,只是在工况6#和7#条件下其平均流速稍有突变。由此表明:控制模型长度的变化对模型迎水面各区域流速的影响相对较小;模型倾角的设置差异对此流速影响非常显著;此外,模型坡比不同、有无防护技术或防护技术不一时,此流速亦存在较大差异。
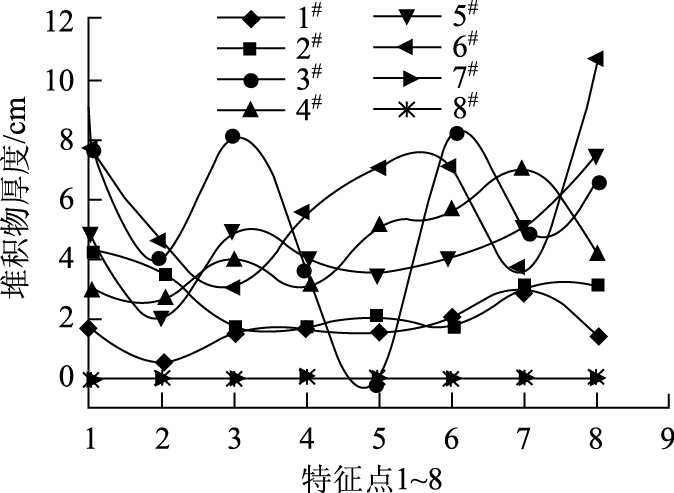
水流对模型冲刷之后,模型下方周围堆积物分布形态通过所选取的特征点处堆积物厚度来拟合,每个模型共设8个特征点,特征点的选取以图 1所建立的三维空间坐标系为参考坐标系。工况1#~8#条件下模型经水流冲刷后周围堆积物分布形态详见图 3所示。
|
| 图 3 各工况特征点1~8处堆积物厚度 Fig. 3 Deposit thickness at characteristic points 1-8 under different working conditions |
| |
结合表 2和图 3分析可知:工况1#~8#条件下,模型下方周围堆积物形态表现为峰和谷,且峰和谷的走向因模型长度、倾角、坡比及防护技术的差异而呈现出不同的趋势;工况1#和2#条件下,两者堆积物厚度较小、不集中,并基本保持一致,且峰谷陡降趋势较平稳、起伏低;工况3#~5#条件下,堆积物厚度较高且分布极不均匀,其中,工况3#条件下堆积物形成的峰谷陡降程度极为显著;工况6#条件下,堆积物厚度较大,分布几乎集中于模型迎水面前方中部;而工况7#和8#条件下,堆积物厚度为零。
由此表明:模型控制长度尺寸越大,堆积物分布形态越不稳定、厚度起伏大;模型倾角对堆积物分布形态的影响程度以90°为特征值,大于或小于此特征值时堆积物体积量较大且分布愈不均匀,当倾角为135°时此现象尤为显著;设有坡比的模型周围堆积物虽较厚,但体积量少且集中;采取防护技术措施可对模型起到完全防冲刷破坏作用。
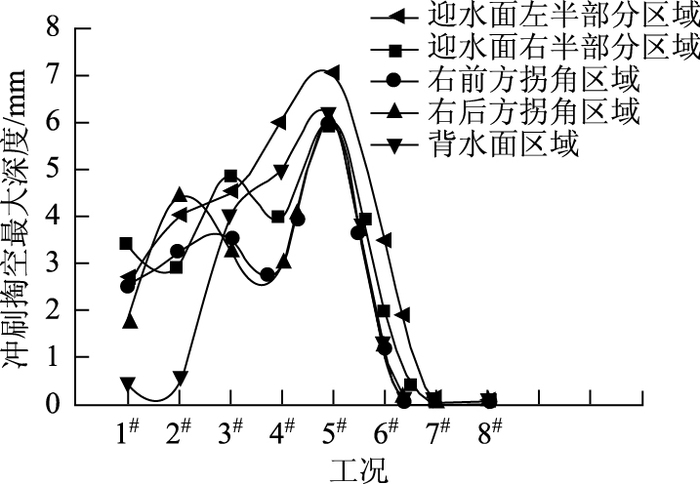
经水流冲刷,模型前方迎水面区域、模型右前方和右后方拐角区域、模型背水面区域会形成一系列近似圆弧凹凸形面,测定各工况条件下前述各区域经水流冲刷后冲刷掏空最大深度,详见图 4。
|
| 图 4 各工况相应区域冲刷掏空最大深度 Fig. 4 Maximum scour depths in corresponding regions of different working conditions |
| |
结合表 2和图 4分析可知:工况1#~8#中,模型经水流冲刷之后,在各区域形成掏槽,冲刷掏空深度分布并不均匀;工况1#~3#条件下,冲刷掏空最大深度总体呈现逐渐增大的变化趋势,工况4#和5#冲刷掏空现象相比略显微弱,且工况5#条件下模型各区域被水流冲刷掏空形成的最大深度比其他工况显著;工况6#~8#条件下,此现象逐渐衰弱,直至工况7#和8#条件下,模型冲刷掏空已不存在;工况1#~8#条件下,冲刷掏空最大深度出现在模型迎水面左半部分区域。
由此表明:在模型尺寸、倾角、坡比及防护技术影响下,模型各区域冲刷掏空现象呈现出各自的特征;模型倾角为135°时,冲刷掏空破非常显著,整个模型近乎完全被掏空,模型岩土材料坍塌形成大量堆积物,因此,在实际工程中,应适当控制桥台倾角大小;模型迎水面与水流冲击直接作用,破坏较其他区域更为显著,实际工程中,应合理设置坡比或采用防护技术等措施对桥台迎水面进行防护。
从试验结果可以看出:不论是采取模拟注浆层隔水防护,还是采取模拟石笼(围堰)防冲刷防护,都能在一定的作用上起到保护路桥结合部位的作用。而对于工程中现有的使用浆砌片石锥坡进行防冲刷破坏虽起到一定作用,但由于片石间水泥砂浆开裂、片石脱落、片石与下部岩土体材料不能有效地结合为一体等缘故,浆砌片石并不能最大限度地发挥防冲刷破坏作用,实际过程中,应对采取何种防护技术措施予以高度的重视。
在设定的冲刷时间内观察整个试验过程中各工况条件下模型水毁破坏现象,以此对试验结束后模型破坏程度进行评价,概括详见表 3。
| 工况 | 破坏现象 | 破坏程度 |
| 1# | 迎水面水位高度下方形成近似圆弧凹凸形面破坏,凸形面出现在两个凹形面中间,岩土体从模型壁掉下向前方平移一段距离,背水面尽是水浸泡而破坏 | 一般破坏 |
| 2# | 与1#相似,但迎水面右半部分某处破坏高度高于水位高度,且绝大部分岩土体被冲刷至右后方拐角区域 | 一般破坏 |
| 3# | 迎水面全部形成破坏,凹凸形面交替连续排布,右侧垮落较大,背水面破坏很严重且不规则 | 大量破坏 |
| 4# | 迎水面破坏现象十分明显,水位高度上方某些部位岩土体垮落,迎水面右半部分区域破坏后呈直线型面,背水面伴有裂隙,有回流和乱流现象 | 大量破坏 |
| 5# | 迎水面全部形成破坏,现象非常明显,形成坡度均匀的脊,右侧及背水面全部垮落,垮落掉块堆积物形成洼且堆积面积较大 | 完全破坏 |
| 6# | 迎水面水位高度下方右侧靠近中部掏空深度相对较深,右侧及背水面均由水浸泡而形成棱状,岩土体被冲刷后绝大部分集中堆积 | 轻微破坏 |
| 7# | 模型保持完好状态 | 未破坏 |
| 8# | 模型表面仅仅有小部分沙脱落,可忽略 | 未破坏 |
2 路桥结合部位水毁破坏有限元分析 2.1 有限元模型的建立
利用ADINA岩土工程有限元分析软件计算,桥台冲刷水毁问题设定为流固耦合(ADINA-FSI)分析,采用FCBI-C单元算法和流场复合积分算法,相互作用的结构模型和流体模型耦合问题通过迭代FSI耦合方法处理。桥台岩土材料遵循Mohr-Coulomb准则,流体采用3Dfluid单元、六面体单元网格,结构体采用3Dsolid单元、四面体单元网格。结构模型采用动力学隐式计算、自动时间步且时间步设置为800步。结构模型底面和根部为全约束,前后两侧、端部以及液面没过桥台时的顶面为流固耦合边界;流体模型底面为wall边界、顶面为自由边界,流体与结构体接触面采用滑动边界。数值计算材料参数见表 4。
| 材料名称 | 密度/(kg·m-3) | 黏度 | 泊松比 | 体积弹性模量/Pa | 弹性模量/Pa | 黏聚力/Pa | 内摩擦角/(°) |
| 桥台 | 1 800 | — | 0.22 | — | 2.56E+007 | 5 000 | 27 |
| 流体 | 1 000 | 0.001 | — | 2.56E+009 | — | — | — |
2.2 数值计算工况
在数值计算中,以桥台伸入流体长度、倾角及坡比为控制变量,共设置6种数值计算工况(见表 5)。
| 工况 | 模型长度/cm | 模型高度/cm | 水位/cm | 模型倾角/(°) | 模型端头形状 | 水流流速/(cm·s-1) | 水流冲刷时间/s | 防护技术 | 桥台坡比 |
| 1# | 20 | 20 | 15 | 90 | 矩形 | 1.5E+4 | 20 | 无 | 0 |
| 2# | 40 | 20 | 15 | 90 | 矩形 | 1.5E+4 | 20 | 无 | |
| 3# | 60 | 20 | 15 | 90 | 矩形 | 1.5E+4 | 20 | 无 | |
| 4# | 40 | 20 | 15 | 45 | 矩形 | 1.5E+4 | 20 | 无 | |
| 5# | 40 | 20 | 15 | 135 | 矩形 | 1.5E+4 | 20 | 无 | |
| 6# | 40 | 20 | 15 | 90 | 矩形 | 1.5E+4 | 20 | 无 | 1:1.5 |
2.3 数值计算结果与分析
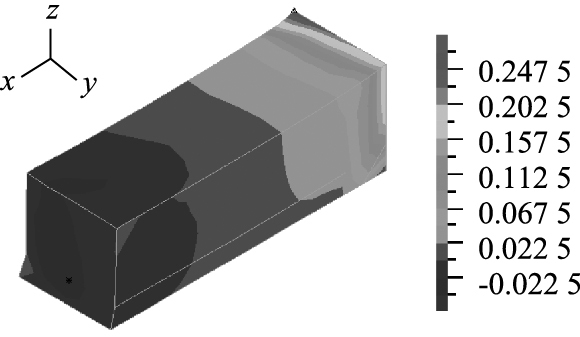
数值计算工况1#条件下,绕流现象较小,结构体迎水面上部自由顶点位移较大,固定的底部和后端发生较大的塑性变形,最大塑性应变接近0.18。数值计算工况2#条件下,漫堤和绕流现象以及结构体迎水面对垂直方向水流的阻挡作用均加强,迎水面上部接近于中部的位移较大,最大塑性应变接近0.30。数值计算工况3#条件下,结构体迎水面水流速度较水流进口初速度降低了约50%,但漫堤和绕流现象更为强烈,水流对前端冲刷破坏加强,迎水面上部接近于中部的位移很大,最大塑性应变(见图 5所示)接近0.32,且提升幅度减小。
|
| 图 5 数值计算工况3#塑性应变云图 Fig. 5 plastic strain nephogram of numerical calculation under working condition 3# |
| |
由此分析表明:在水流作用下结构体力学破坏基本近似于悬臂梁结构;模型结构体冲刷破坏现象是固定的底部和后端产生较大的拉应力而致;当结构物圧缩流体导致过水断面减小时,水流对结构物整体破坏较大。
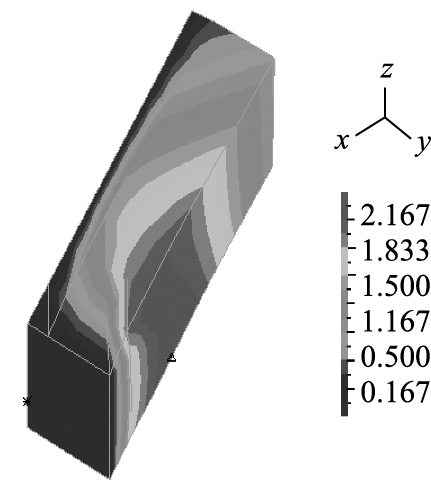
数值计算工况4#条件下,结构体背水面下部形成较大的位移(见图 6所示),背水面前端和下部固定端产生较大的塑性变形,绕流冲刷现象加强,背水面角部先破坏并逐步发展到中部。数值计算工况5#条件下,绕流范围减小,模型结构体表面静水压力提高,迎水面中部首先出现掏空,背水面表面出现冲刷,且位移显著。
|
| 图 6 数值计算工况4#位移云图(单位:cm) Fig. 6 displacement nephogram of numerical calculation under working condition 4#(unit:cm) |
| |
由此分析表明:设有倾角的模型改变了迎水面的水流方向;对比数值计算工况2#和4#可知,工况4#结构体前墙外侧水流流速出现较小的水力梯度,流速变化相对稳定,迎水面前墙角位水流出现分流;对比数值计算工况4#和5#可知,工况5#靠近结构体前墙外侧水流流速较大,结构体迎水面流速方向变为近135°,流速较进口流速降低30%左右,但背水面流速与水流进口流速接近,具备形成局部湍流或环流的可能。
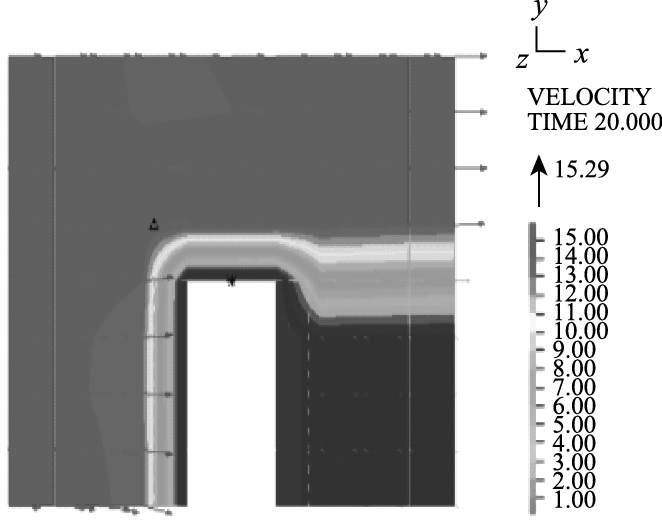
数值计算工况6#条件下,坡比为1:1.5的迎水面和背水面使水流流速产生有效的分解,流场矢量云图(见图 7所示)中明显出现沿坡面的速度矢量,冲刷主要发生在坡面中部;对比数值计算工况2#和6#可知,相同流速和冲刷时间下,工况6#条件下结构体位移非常小。由此分析表明:在坡面具有良好的防冲刷技术构造时,梯形截面式结构体具有较强的抗冲刷能力。
|
| 图 7 数值计算工况6#流场矢量云图 Fig. 7 Flow field vector nephogram of numerical calculation under working condition 6# |
| |
3 模型试验结果与数值计算结果对比分析
模型试验中,由测定的水流平均速度曲线(见图 2所示)及观测的模型破坏现象(见表 3所示)分析可知:模型倾角的设置差异对模型迎水面水流流速影响非常显著;此外,模型伸入流体长度越长模型结构体破坏越明显。而由数值计算分析可知:当结构物圧缩流体导致过水断面减小时,水流对结构物整体破坏较大;此外,设有倾角的模型改变了迎水面的水流方向从而使流速发生显著变化。模型试验结果与数值计算结果相吻合。
模型试验中,由测定的堆积物分布和厚度(见图 3所示)、模型冲刷掏空最大深度(见图 4所示)及观测的模型破坏现象(见表 3所示)分析可知:设有坡比的模型堆积物分布几乎集中于模型迎水面前方中部,且冲刷掏空最大深度较小;模型伸入流体长度越长,堆积物形成的峰谷陡降趋势越显著,且冲刷掏空最大深度越深;此外,模型倾角为135°时,堆积物体积量非常大,冲刷掏空最大深度显著,背水面垮落破坏极其严重。而由数值计算分析可知:设有坡比的模型使水流产生了有效的分解,沿坡面出现速度矢量(见图 7所示),冲刷主要发生在坡面中部;模型伸入流体长度越长,绕流漫堤现象及阻水作用越强,结构体塑性应变(见图 5所示)和位移越大,冲刷破坏越剧烈;此外,设有倾角的模型结构体背水面破坏严重,位移显著(见图 6所示)。模型试验结果与数值计算结果相吻合。
4 结论在前人研究成果的基础上,通过Fr相似准则,采用正交试验设计方法,进行模型试验,利用ADINA有限元数值计算软件建立了路桥结合部位水毁破坏三维有限元模型,着重研究了模型伸入流体长度、倾角、坡比及有无防护措施对模型水毁破坏的影响程度。得到以下结论:
(1) 模型伸入流体长度分别为20、40和60 cm工况条件下,水流冲刷或浸泡作用对模型结构体造成的破坏程度逐渐加深,且长度为60 cm时模型结构体大量破坏。
(2) 模型倾角设计为45°, 90°和135°时,倾角为135°所对应的模型结构体受水流冲刷后形成的堆积物体积量大且分布不集中,冲刷掏空深度显著,模型近乎完全破坏。
(3) 模型坡比为1:1.5时,坡面能使水流流速产生有效分解,具有较强的抗冲刷能力;采取注浆层或围堰防护措施可对模型结构体起到完全的保护作用。
(4) ADINA有限元数值计算结果与模型试验结果较为相近,两者相吻合,为路桥结合部位水毁破坏研究提供重要参考。
| [1] | 刘伟军. 关于公路水毁的成因分析及防治措施探讨[J]. 江西建材, 2016(13): 208-209 LIU Wei-jun. Discussion on Cause Analysis and Prevention Measures of Highway Flood Damage[J]. Jiangxi Building Materials, 2016(13): 208-209 |
| [2] | 罗青, 熊建安. 路基水毁特征及边坡稳定性有限元分析[J]. 交通建设与管理, 2014(24): 83-85 LUO Qing, XIONG Jian-an. Finite Element Analysis on Characteristics of Roadbed Flood Damage and Slope Stability[J]. Transportation Construction & Management, 2014(24): 83-85 |
| [3] | 高明永, 田伟平, 王栋. 路基水毁灾害原因分析及防治措施研究[J]. 华东公路, 2012(2): 38-40 GAO Ming-yong, TIAN Wei-ping, WANG Dong. Roadbed Disasters Cause Analysis and Prevention Measures[J]. East China Highway, 2012(2): 38-40 |
| [4] | 王继宏. 浅议公路水毁的成因与防治[J]. 甘肃科技纵横, 2009, 38(1): 168-169 WANG Ji-hong. Discussion on Causes and Prevention of Highway Water Damage[J]. Scientific & Technical Information of Gansu, 2009, 38(1): 168-169 |
| [5] | 胡建刚, 张亮, 苟睿, 等. 公路水毁的破坏型式、成因及防治对策初步研究[J]. 公路交通科技, 2005, 22(增1): 26-29 HU Jian-gang, ZHANG Liang, GOU Rui, et al. The Destroy Type, Origin and Controlling Measurement of Water Damage of Highway[J]. Journal of Highway and Transportation Research and Development, 2005, 22(S1): 26-29 |
| [6] | 马保成. 公路水毁灾害识别技术研究[D]. 西安: 长安大学, 2011. MA Bao-cheng. Research on Highway Flood Disaster Identification Technology[D]. Xi'an:Chang'an University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10710-1012142429.htm |
| [7] | 孙有财. 浅谈山区公路水毁的防治技术[J]. 科技创新与应用, 2015(6): 157 SUN You-cai. Talking about Control Technology of Mountainous Highway Washout[J]. Technology Innovation and Application, 2015(6): 157 |
| [8] | 齐洪亮, 田伟平, 李家春. 山区沿河路基水毁灾害风险定量评价方法[J]. 自然灾害学报, 2014, 23(2): 271-277 QI Hong-liang, TIAN Wei-ping, LI Jia-chun. Quanti-tative Risk Assessment of Subgrade Flood-damage Along River in Mountainous Areas[J]. Journal of Natural Disasters, 2014, 23(2): 271-277 |
| [9] | 李俊, 刘鹏. 山区公路路基水毁类型划分[J]. 华东公路, 2016(1): 69-72 LI Jun, LIU Peng. Division of Subgrade Flood Damage Type in Mountain Area[J]. East China Highway, 2016(1): 69-72 |
| [10] | 周美林, 肖政, 蒋昌波. 沿河公路丁坝群水毁防护平面二维水流数值模拟研究[J]. 水运工程, 2007(8): 17-20 ZHOU Mei-lin, XIAO Zheng, JIANG Chang-bo. Numeral Simulation of Planar 2-D Flow with Spur-dikes Protecting Riverside Subgrade[J]. Port & Waterway Engineering, 2007(8): 17-20 |
| [11] | 沈水进, 孙红月, 朱汉华. 台风暴雨引发公路水毁规律分析及防灾对策[J]. 公路工程, 2011, 36(6): 6-10, 21 SHEN Shui-jin, SUN Hong-yue, ZHU Han-hua. Law Analysis and Control Measures of Highway Flood Hazard Caused by Typhoon Rainstorm[J]. Highway Engineering, 2011, 36(6): 6-10, 21 |
| [12] | 李宾. 国道217线天山公路冲刷模型试验及应用[J]. 公路工程, 2015, 40(1): 96-101, 106 LI Bin. The Erosion Model Test and Application of Tianshan Road of G217[J]. Highway Engineering, 2015, 40(1): 96-101, 106 |
| [13] | 马年祖, 建德琳, 代玉莉, 等. 山岭重丘区道路改扩建路基持续降雨渗流数值模拟[J]. 公路交通科技, 2016, 33(9): 31-37, 45 MA Nian-zu, JIAN De-lin, DAI Yu-li, et al. Numerical Simulation of Subgrade Persistent Rainfall Seepage of Reconstructed Highway in Mountainous and Heavy-hilly Area[J]. Journal of Highway and Transportation Research and Development, 2016, 33(9): 31-37, 45 |
| [14] | YOUSSEF M A, PRADHAN B, HASSAN A M. Flash Flood Risk Estimation Along the St.Katherine Road, Southern Sinai, Egypt Using GIS Based Morphometry and Satellite Imagery[J]. Environmental Earth Sciences, 2011, 62(3): 611-623 |
| [15] | KHAN MI U, MESBAH M, FERREIRA L, et al. Assessment of Flood Risk to Performance of Highway Pavements[C]//Proceedings of the Institution of Civil Engineers-Transport. New South Wales:Thomas Telford Ltd, 2017:1-10. |
| [16] | DAS T, IDRIS I I, BASAK B, et al. Key Factors Affecting Highway Freight Transportation Disruptions at Post Disaster Phase[C]//Australasian 38th Transport Research Forum (ATRF). Melbourne:[s. n.], 2016. |
| [17] | LU D H, TIGHE S L, XIE W C. Pavement Fragility Modeling Framework and Build-in Resilience Strategies for Flood Hazard, 17-01735[R]. Washington, D. C.:Transportation Research Board, 2017. |
| [18] | GILLESPIE N, UNTHANK A, CAMPBELL L, et al. Flood Effects on Road-stream Crossing Infrastructure:Economic and Ecological Benefits of Stream Simulation Designs[J]. Fisheries, 2014, 39(2): 62-76 |
| [19] | LEESON D, FULMER C, HERON K. Flood Resilient Bridge Design:Case Studies from Challenging Design Environments[C]//Austroads 9th Bridge Conference. Sydney:Austroads, 2014:1-13. |
| [20] | BRIAUD J L, MADDAH L. Minimizing Roadway Embankment Damage From Flooding, Project 20-05(Topic 46-16)[R]. Washington, D.C.:Transportation Research Board, 2016. |
 2017, Vol. 34
2017, Vol. 34
