扩展功能
文章信息
- 王皓磊, 邵旭东
- WANG Hao-lei, SHAO Xu-dong
- 带加劲肋钢-混凝土组合蜂窝梁开孔腹板的抗剪性能
- Shearing Performance of Perforated Web in Steel-concrete Composite Castellated Beam with Reinforced Webs
- 公路交通科技, 2017, 34(8): 66-75
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(8): 66-75
- 10.3969/j.issn.1002-0268.2017.08.010
-
文章历史
- 收稿日期: 2016-05-26
2. 湖南大学 土木工程学院, 湖南 长沙 410082
2. School of Civil Engineering, Hunan University, Changsha Hunan 410082, China
带加劲肋钢-混凝土组合蜂窝梁是一种新型的桥梁结构形式[1],其箱梁腹板成排开孔,结构通透,造型新颖,抗弯刚度大于扩张前截面[2-3],截面效率高;采用圆形孔,避免孔角较大的应力集中[2-5];在孔洞间设置竖向加劲肋,能有效防止腹板的屈曲失稳[5],提高承载能力。其结构形式如图 1所示。

|
| 图 1 带加劲肋钢-混凝土组合蜂窝梁构造图 Fig. 1 Structure of steel-concrete composite castellated beam with reinforced webs |
| |
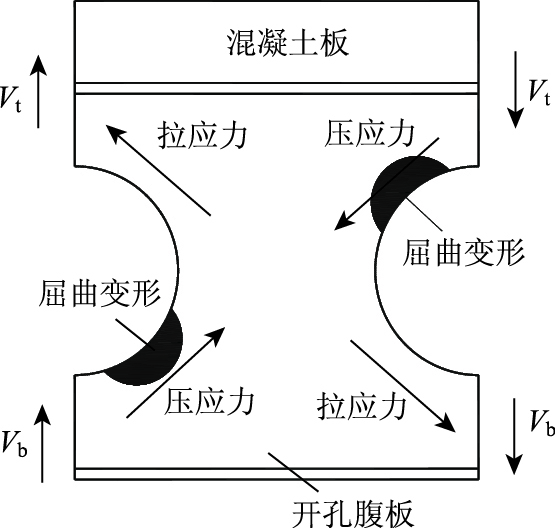
组合蜂窝梁腹板成排开孔后,主要削弱了其抗剪强度和抗剪稳定性。各孔洞之间的实腹截面, 在荷载相对较小时便有可能发生屈曲[6-8],为防止屈曲过早产生,在实腹板处设置竖向加劲肋,将腹板分为若干区格是十分必要的,如图 1所示。文献[5]的研究表明,布置竖向加劲肋是防止孔洞间腹板屈曲的一种有效措施。在剪力次弯矩的作用下,竖向加劲肋之间的开孔腹板孔洞边缘形成压应力和拉应力交替分布的峰值区域,受力和可能的屈曲模式如图 2所示,显然其剪切屈曲模式有别于钢实腹板。对实腹板抗剪承载能力的计算时,最常用的是拉力场理论[9-13],其认为腹板的抗剪承载能力由弹性屈曲荷载和张力场提供的承载力组成。对于组合蜂窝梁的开孔腹板,由于孔洞的存在,腹板屈曲后的拉力场被破坏,用该理论求解已不适用,且目前尚无合适的计算公式。同时鉴于开孔结构本身的复杂性,本研究将采用有限元方法对开孔腹板的抗剪性能进行研究。
|
| 图 2 开孔腹板受力简图 Fig. 2 Force diagram of perforated web |
| |
1 开孔腹板弹性剪切屈曲分析
板件抵抗屈曲的能力采用力的形式进行表示[13],即:
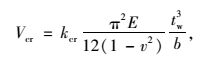
|
(1) |
式中,kcr为板的弹性屈曲系数;b, tw为板的高度和厚度;E, v为弹性模量、泊松比。
组合梁的钢腹板,通常认为其左右两边简支于横向加劲肋,上下两边简支或固支于上下翼缘。对于四边简支的实腹板,其弹性屈曲系数为:
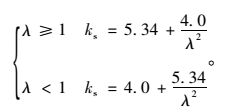
|
(2) |
左右两边简支,上下两边固支的实腹板,其弹性屈曲系数为:
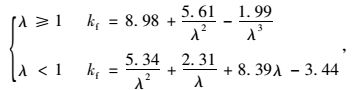
|
(3) |
式中λ为板的宽高比,λ=a/b。
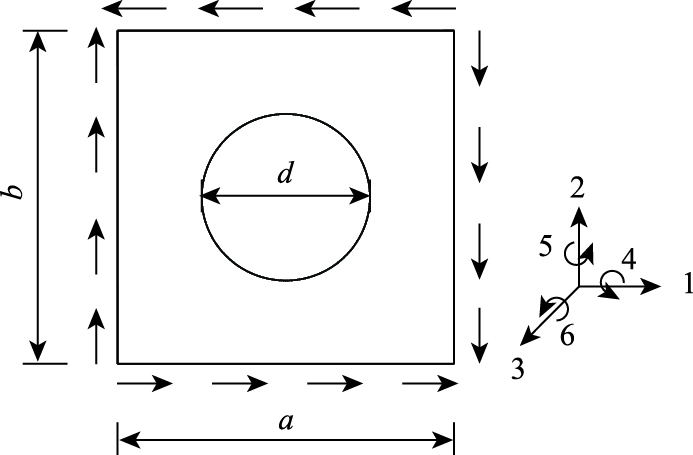
1.1 分析模型有限元模型和加载方式如图 3、图 4所示。开孔腹板采用4节点shell63单元模拟,材料参数为:弹性模量E=210 GPa,泊松比ν=0.3。采用映射网格分网,网格的密度保证分析结果具有足够的精度。荷载施加在板的4个边界节点上。分析模型中开孔板的边界条件分别为:(1) 四边简支时,约束每条边上节点的平动自由度3、左上角节点的平动自由度1、左下角节点的平动自由度1和2;(2) 两边简支,两边固支时,约束每条边上节点的平动自由度3、上下边的转动自由度4、左上角节点的平动自由度1、左下角节点的平动自由度1和2。

|
| 图 3 有限元模型(a/b=1.0, d/b=0.5) Fig. 3 Finite element model |
| |
|
| 图 4 有限元模型的荷载及约束条件 Fig. 4 Loading and constraint condition of FE model |
| |
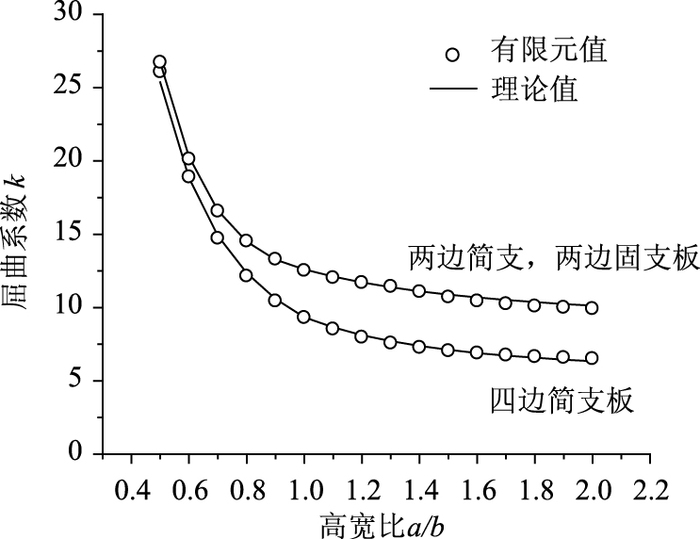
进行相关计算前首先对相同约束条件下的未开孔矩形板进行弹性屈曲分析,以验证上述分析模型的正确性。同时,按式(2) 和式(3) 分别计算得到矩形板的剪切屈曲系数,二者计算结果如图 5所示。
|
| 图 5 矩形板的剪切屈曲系数 Fig. 5 Shear buckling coefficients of rectangular flat-plate |
| |
从图 5可以看出,有限元分析结果与理论值吻合良好,说明计算模型是正确可行的。
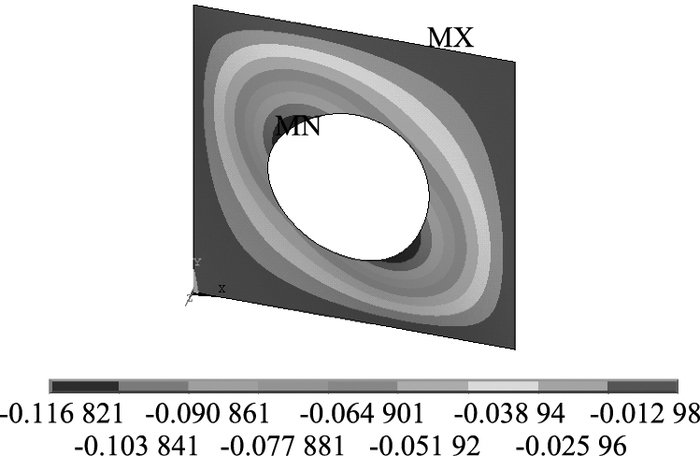
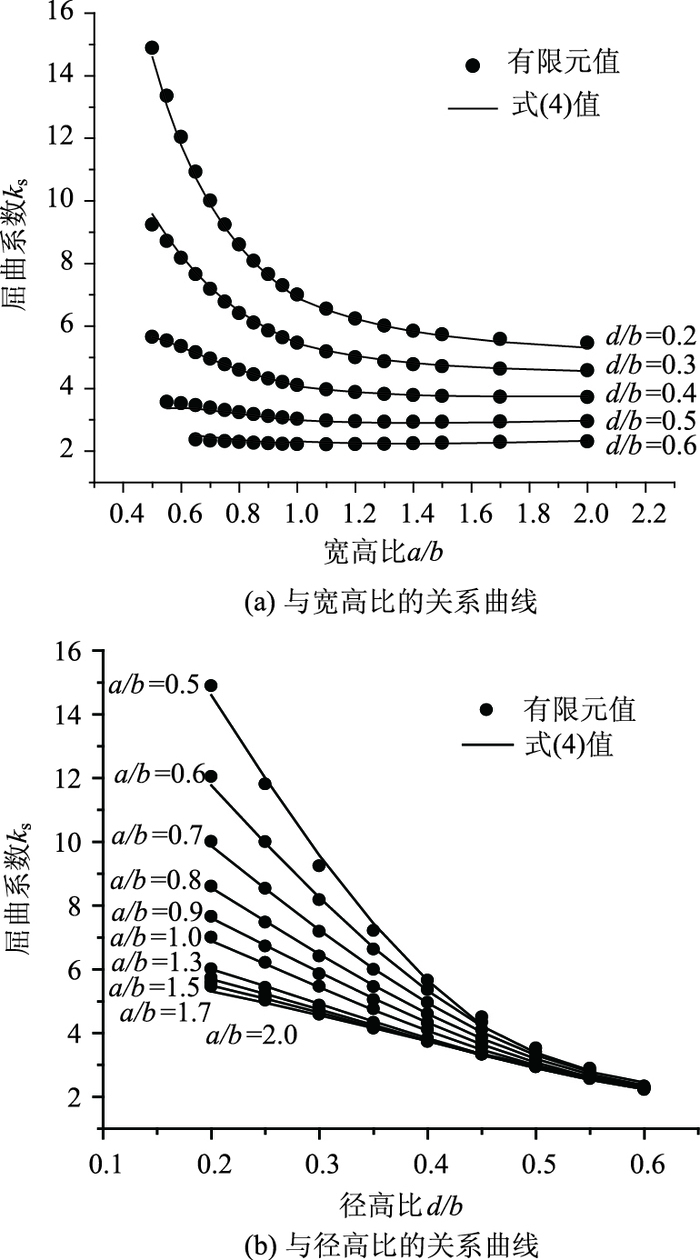
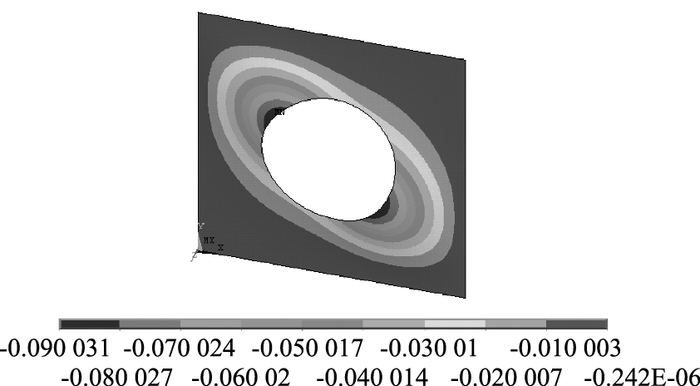
1.2 四边简支开孔板在四边简支开孔板分析模型中,板厚度取为tw=3 mm,高度取为b=450 mm,b保持不变,宽高比a/b从0.5变化至2 (即板的长度a在225~900 mm间变化),径高比d/b从0.2变化至0.6 (即直径d在90~270 mm间变化)。四边简支开孔板的典型屈曲波形如图 6所示,由计算得到的屈曲荷载值根据式(1) 反算得开孔板的剪切屈曲系数ks,ks随宽高比a/b以及径高比d/b的变化规律如图 7、图 8所示。可以看出,ks随a/b和d/b的增大而减小,当a/b增加至1.5~2.0时,ks已基本趋于一致。
|
| 图 6 四边简支开孔腹板-阶屈曲波形(单位:m)(a/b=1.0, d/b=0.5) Fig. 6 First-order buckling mode shape of quadrilateral simply supported perforated web (unit:m) (a/b=1.0, d/b=0.5) |
| |
|
| 图 7 四边简支开孔板剪切屈曲系数的关系曲线 Fig. 7 Curves of shear buckling coefficient for quadrilateral simply supported perforated web |
| |
|
| 图 8 两边简支、两边固支开孔腹板一阶屈曲波形(单位:m) (a/b=1.0, d/b=0.5) Fig. 8 First-order buckling mode shape of two-side simply supported and two-side fixed perforated web(unit:m) (a/b=1.0, d/b=0.5) |
| |
在式(2) 中引入系数ρs对径高比和宽高比进行修正,并令α=d/b,则四边简支开孔腹板的剪切屈曲系数ks可表示为:
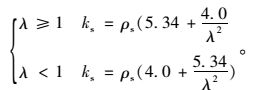
|
(4) |
通过数据拟合得到ρs可表达为:
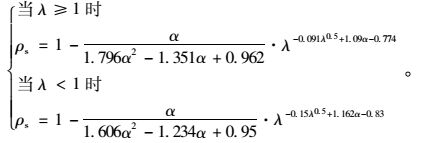
|
(5) |
当径高比α=0时,式(4) 还原为未开孔矩形板剪切屈曲系数计算式(2)。
图 7表明式(4) 计算值与有限元值吻合良好。
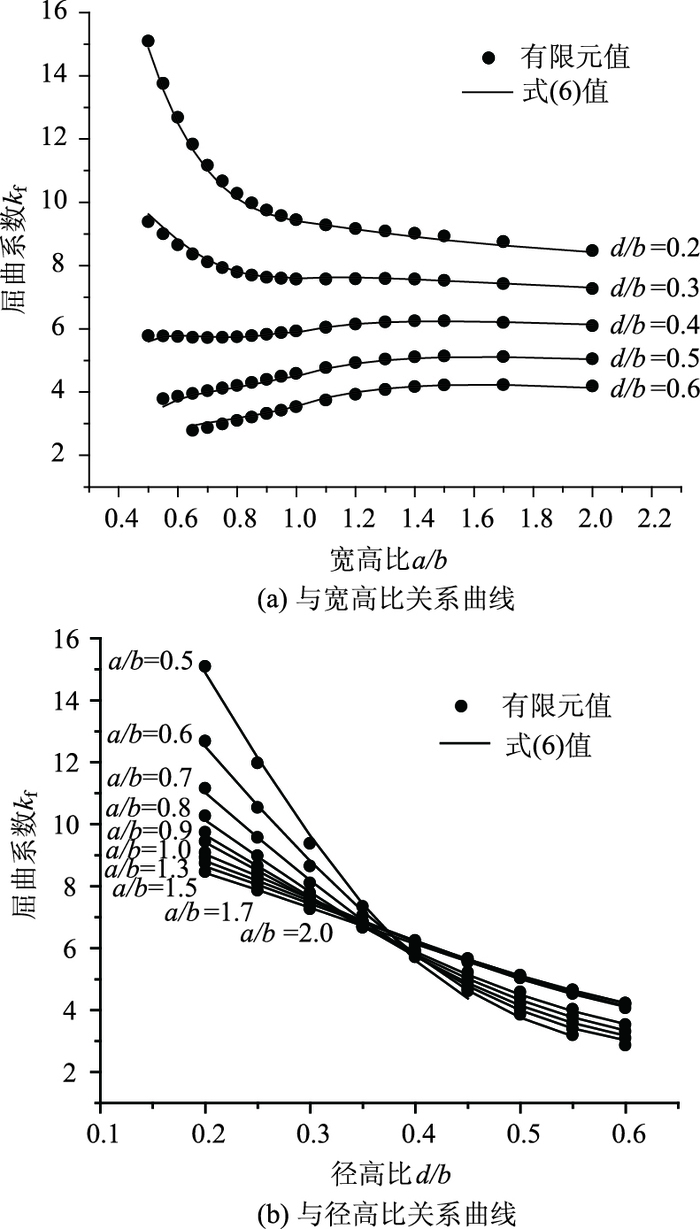
1.3 两边简支、两边固支开孔板组合梁的混凝土翼缘和钢翼缘约束了开孔腹板的转动,其刚度较大时,开孔腹板的上下边可视为固支,两侧仍可视为简支于加劲肋。在两边简支、两边固支开孔板分析模型中,板厚度tw=3 mm,高度b=450 mm,b保持不变,宽高比a/b从0.5变化至2 (即板的长度a在225~900 mm间变化),径高比d/b从0.2变化至0.6 (即直径d在90~270 mm间变化)。两边简支、两边固支开孔板的典型屈曲波形见图 8,由计算得到的屈曲荷载值根据式(1) 反算得开孔板的剪切屈曲系数kf,kf随宽高比a/b以及径高比d/b的变化规律见图 9。可以看出,kf的变化规律与ks相似。
|
| 图 9 两边简支,两边固开孔板剪切屈曲系数的关系曲线 Fig. 9 Relation curves of shear buckling coefficient for two-side simply supported and two-side fixed perforated web |
| |
同样,引入系数ρf对径高比和宽高比进行修正,两边简支、两边固支开孔腹板的剪切屈曲系数kf的计算公式为:
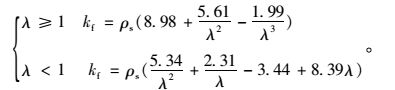
|
(6) |
修正系数ρf通过数据拟合得到:
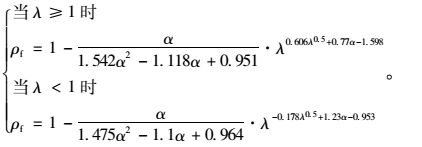
|
(7) |
当径高比α=0时,式(6) 还原为未开孔矩形板剪切屈曲系数计算式(3)。
由图 9可以看出式(6) 计算值与有限元值吻合良好。
而实际上,翼缘对腹板的约束介于简支和固支之间,可引入约束系数β=bftf3/btw3表征翼缘对腹板的约束程度,则考虑了翼缘约束程度的开孔腹板屈曲系数kcr即可按式(8) 计算[14]:
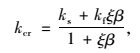
|
(8) |
式中,ks为四边简支开孔腹板的剪切屈曲系数,按式(4) 计算;kf为两边简支、两边固支开孔腹板的剪切屈曲系数, 按式(6) 计算;ξ为腹板宽高比的影响系数。
通过对不同β值时504个分析模型的计算,经过数据拟合,ξ可表达为:
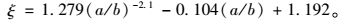
|
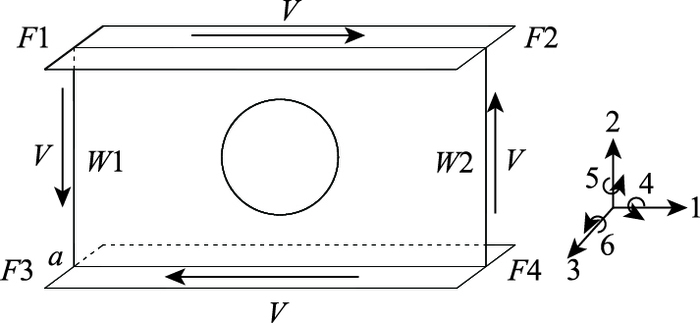
如图 1所示组合蜂窝梁的结构形式,腹板相邻孔洞之间设置有一定间距的竖向加劲肋。一般认为竖向加劲肋刚度足够大,腹板开始发生屈曲变形时,加劲肋不发生变形[15-16]。因此,采用图 10所示模型分析开孔腹板的抗剪极限承载能力。
|
| 图 10 开孔腹板抗剪承载能力分析模型 Fig. 10 Analytic model of shearing resistance of perforated web |
| |
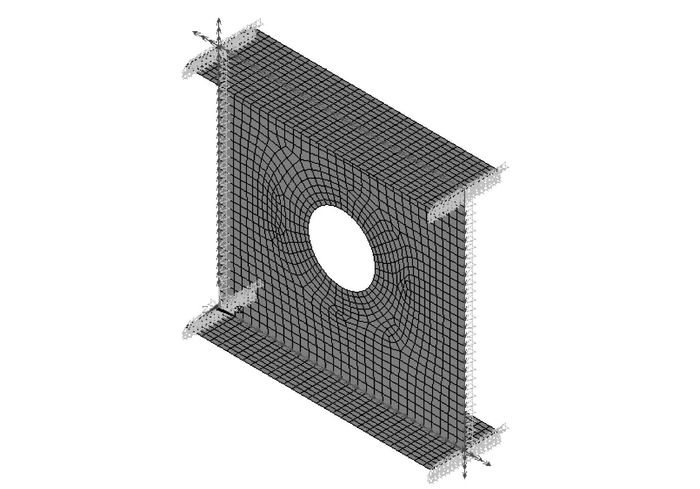
有限元分析时,采用四节点壳单位shell181模拟模型的翼缘和腹板,模型边界条件为:开孔腹板两对边W1和W2简支,约束其平动自由度3;约束翼缘F1,F2,F3和F4的平动自由度2,3和转动自由度5;约束角点a的平动自由度1。在腹板四边节点上施加荷载,有限元模型如图 11所示。
|
| 图 11 开孔腹板抗剪承载能力有限元模型 Fig. 11 Finite element model for calculating shearing resistance of perforated web |
| |
2.2 开孔腹板的抗剪极限承载能力
考虑几何和材料双重非线性,采用图 10、图 11有限元模型对开孔腹板的抗剪承载能力进行分析,计算中取特征值屈曲一阶模态作为变形形态,暂时不考虑初始缺陷的影响,即在模型中引入初始缺陷幅值b/30 000(远小于规范限值)使得模型产生面外变形。模型的几何尺寸和材料参数:腹板高b=450 mm,翼缘bf/b=0.3,翼缘约束参数β=30,泊松比μ=0.3,弹性模量E=210 GPa。分析变量为:宽高比a/b,径高比d/b,腹板纤细比b/tw和屈服应力fy。
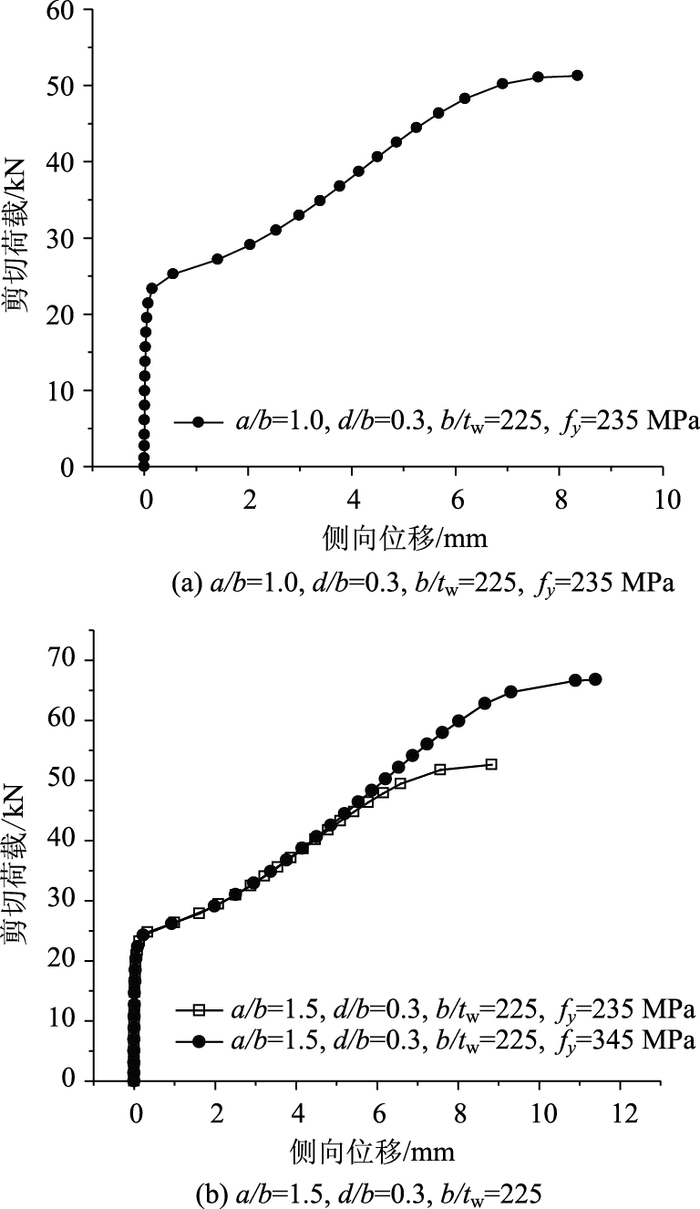
图 12给出了开孔腹板破坏时典型的剪切荷载-侧向位移曲线,其中侧向位移为剪切荷载作用下发生最大侧向变形节点的位移值。由图 12可知,虽然腹板由于孔洞的存在破坏了拉力场,但开孔腹板仍可发展一部分屈曲后强度,剪力作用下开孔腹板承载能力由两部分组成:弹性屈曲荷载Vcr和屈曲后强度Vpb。开孔腹板的弹性屈曲荷载Vcr可按式(1) 计算。对于图 12(a)所分析模型,可计算得:ks=5.45,kf=7.61,ξ=2.37,kcr=7.58,则Vcr=25.6 kN,与曲线中有限元结果吻合良好。各模型计算结果如表 1所示。
|
| 图 12 开孔腹板抗剪承载能力 Fig. 12 Shearing resistance of perforated web |
| |
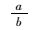 |
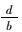 |
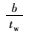 |
fy/
MPa |
Vpb/
kN |
Vpb/
kN |
Vu=Vcr+
Vpb/kN | |
| FEM | 式(8) | ||||||
| 0.7 | 0.3 | 300 | 235 | 11.1 | 11.6 | 16.2 | 27.3 |
| 0.7 | 0.3 | 225 | 235 | 27.1 | 27.4 | 17.3 | 44.5 |
| 1 | 0.3 | 300 | 235 | 10.3 | 10.8 | 20.8 | 31.1 |
| 1 | 0.3 | 225 | 235 | 24.5 | 25.6 | 26.7 | 51.3 |
| 1 | 0.5 | 300 | 235 | 6.6 | 6.7 | 13.8 | 20.4 |
| 1 | 0.5 | 225 | 235 | 15.2 | 15.9 | 17 | 32.2 |
| 1.5 | 0.3 | 300 | 235 | 10.3 | 10.8 | 21.1 | 31.4 |
| 1.5 | 0.3 | 225 | 235 | 24.7 | 25.7 | 28 | 52.6 |
| 1.5 | 0.3 | 225 | 345 | 24.7 | 25.7 | 42.1 | 66.8 |
| 1.5 | 0.5 | 300 | 235 | 7.4 | 7.8 | 15.3 | 22.7 |
| 1.5 | 0.5 | 225 | 235 | 17.5 | 18.4 | 19.3 | 36.8 |
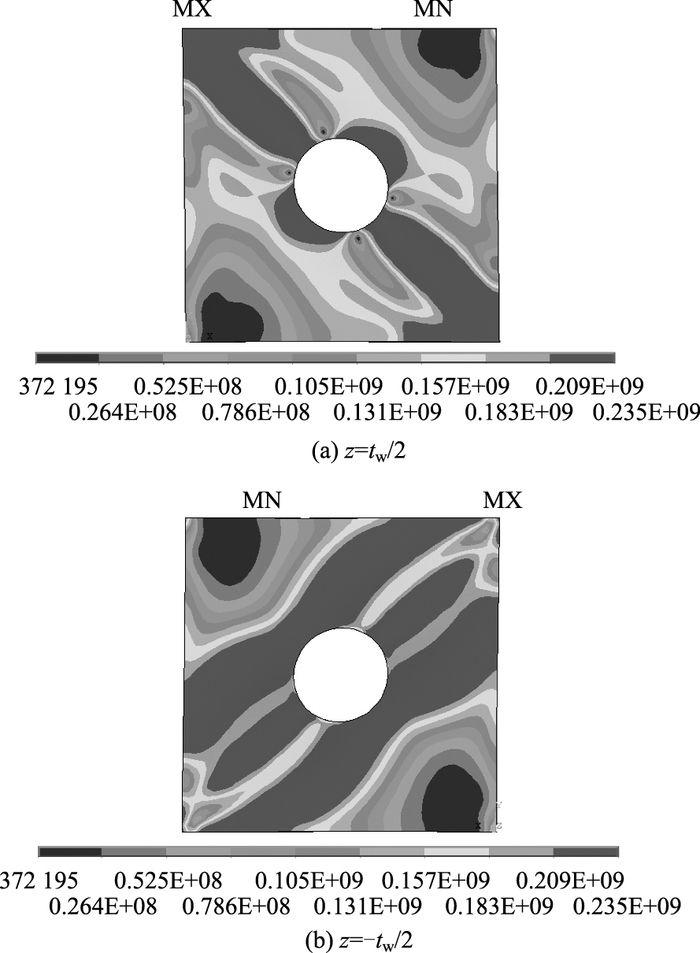
开孔腹板发生弹性屈曲后,随着荷载的增加,开始发展屈曲后强度,在这一过程中,腹板斜向拉力与由于面外变形所引起的弯曲应力不断增大,拉力带范围内钢腹板材料逐渐屈服,与未开孔腹板不同,由于应力集中的影响,开孔腹板孔洞周围材料也随之屈服。图 13给出了开孔腹板破坏时,腹板材料屈服区域在两侧的分布,由图可知由于弯曲应力的影响,屈服区域在腹板两侧的分布并不一致。
|
| 图 13 开孔腹板破坏时屈服区域(单位:Pa) (a/b=1.0, d/b=0.3, b/tw=225, fy=235 MPa) Fig. 13 Yield zone of perforated web at failure (unit:Pa) (a/b=1.0, d/b=0.3, b/tw=225, fy=235 MPa) |
| |
为进一步量化弹性屈曲荷载Vcr和屈曲后荷载Vpb对开孔腹板抗剪承载能力的贡献,采用不同的变量值,对开孔腹板的抗剪承载能力进行了更为广泛的有限元分析,分析模型的几何尺寸和材料参数取为:考虑到翼缘对腹板的屈曲后承载能力影响很小[14, 16],翼缘尺寸统一取为宽bf=0.3b=135 mm,约束参数β=30,腹板高b=450 mm,翼缘宽bf=0.3b=135 mm,翼缘约束参数β=30,宽高比a/b=0.7,1,1.5,径高比d/b=0.3,0.4,0.5,腹板纤细比b/tw=130~400,屈服应力fy=235,345 MPa,泊松比μ=0.3,弹性模量E=210 GPa,初始缺陷幅值为b/30 000。相应的计算结果如表 2~表 5所示。
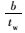 |
fy/
MPa |
Vp/
kN |
Vu/
kN |
Vcr/
kN |
Vpb=Vu-
Vcr /kN | 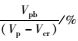 |
| 100 | 235 | 196.1 | 189.1 | — | — | — |
| 130 | 235 | 150.8 | 123.7 | 109.3 | 14.4 | 34.7 |
| 160 | 235 | 122 | 77.2 | 64.1 | 13.1 | 22.6 |
| 180 | 235 | 109 | 64 | 50.7 | 13.3 | 22.8 |
| 200 | 235 | 98.1 | 54.2 | 37.9 | 16.3 | 27.1 |
| 200 | 345 | 144 | 70.8 | 37.9 | 32.9 | 31 |
| 225 | 235 | 87.2 | 44.8 | 26.5 | 18.3 | 29.9 |
| 250 | 235 | 78.5 | 37.8 | 19.4 | 18.4 | 31.2 |
| 300 | 235 | 65.4 | 28 | 11.4 | 16.6 | 30.7 |
| 300 | 345 | 96 | 36.6 | 11.4 | 25.2 | 29.8 |
| 350 | 235 | 56.7 | 22.2 | 6.8 | 15.4 | 30.9 |
| 400 | 235 | 48 | 16.9 | 4.3 | 12.6 | 28.9 |
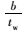 |
fy/
MPa |
Vp/
kN |
Vu/
kN |
Vcr/
kN |
Vpb=Vu-
Vcr /kN | 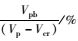 |
| 90 | 235 | 217.9 | 209.1 | — | — | — |
| 112 | 235 | 178.7 | 166.9 | — | — | — |
| 130 | 235 | 148.2 | 123.4 | 107.2 | 16.2 | 39.5 |
| 150 | 235 | 130.8 | 100.6 | 84.2 | 16.4 | 35.2 |
| 150 | 345 | 192 | 126 | 84.2 | 41.8 | 38.8 |
| 170 | 235 | 113.3 | 79.7 | 57.9 | 21.8 | 39.4 |
| 200 | 235 | 98.1 | 62.6 | 37.7 | 24.9 | 40.8 |
| 225 | 235 | 87.2 | 51.3 | 24.5 | 26.8 | 42.8 |
| 250 | 235 | 78.5 | 42.9 | 18.6 | 24.3 | 40.6 |
| 300 | 235 | 65.4 | 31.4 | 9.7 | 21.7 | 39 |
| 350 | 235 | 56.7 | 24.6 | 6.3 | 18.3 | 36.3 |
| 400 | 235 | 48 | 18.4 | 3.1 | 15.3 | 34.1 |
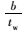 |
fy/
MPa |
Vp/
kN |
Vu/
kN |
Vcr/
kN |
Vpb=Vu-
Vcr /kN | 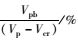 |
| 100 | 235 | 167.2 | 178 | — | — | — |
| 125 | 235 | 133.8 | 122.3 | 114.5 | 7.8 | 40.4 |
| 140 | 235 | 119.3 | 100.8 | 89.4 | 11.4 | 38.1 |
| 160 | 235 | 104.1 | 80.9 | 63.9 | 17 | 42.3 |
| 160 | 345 | 152.8 | 100.4 | 63.9 | 36.5 | 41.1 |
| 180 | 235 | 92.9 | 66.4 | 45.6 | 20.8 | 43.9 |
| 200 | 235 | 83.6 | 55.3 | 33.5 | 21.8 | 43.5 |
| 225 | 235 | 74.3 | 45.2 | 24 | 21.2 | 42.1 |
| 250 | 235 | 66.9 | 37.8 | 17.9 | 19.8 | 40.4 |
| 300 | 235 | 55.8 | 27.8 | 10.5 | 17.3 | 38.2 |
| 350 | 235 | 48.3 | 21.8 | 6.4 | 15.4 | 36.7 |
| 400 | 235 | 40.9 | 16.4 | 3.5 | 12.9 | 34.5 |
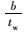 |
fy/
MPa |
Vp/
kN |
Vu/
kN |
Vcr/
kN |
Vpb=Vu-
Vcr /kN | 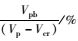 |
| 90 | 235 | 151.8 | 146.5 | — | — | — |
| 125 | 235 | 109.3 | 82.4 | 72.2 | 10.2 | 27.5 |
| 150 | 235 | 91.1 | 61.2 | 49.5 | 11.7 | 28 |
| 150 | 345 | 133.7 | 80.8 | 49.5 | 31.3 | 37.2 |
| 170 | 235 | 78.9 | 48.9 | 34.3 | 14.6 | 32.7 |
| 200 | 235 | 68.3 | 38.7 | 21.2 | 17.5 | 37.2 |
| 225 | 235 | 60.7 | 32.1 | 15.1 | 17 | 37.3 |
| 250 | 235 | 54.7 | 27.3 | 11.4 | 15.9 | 36.8 |
| 250 | 345 | 80.2 | 36.6 | 11.4 | 25.2 | 36.6 |
| 300 | 235 | 45.5 | 20.7 | 6.7 | 14 | 36 |
| 350 | 235 | 39.5 | 16.7 | 4.3 | 12.5 | 35.5 |
| 400 | 235 | 33.4 | 12.9 | 2.6 | 10.3 | 33.4 |
考虑非弹性屈曲的作用,定义非弹性屈曲荷载Vcrin为:
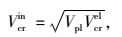
|
(9) |
式中Vcrel为弹性屈曲荷载。
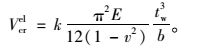
|
(10) |
Vpl为比例极限,Vpl=0.8Vp,Vp为开孔腹板塑性抗剪强度,按如下方法求得:
直径为d的圆孔可等效为0.45d×0.9d的矩形孔[17-18],如图 14 (a)所示。腹板受剪时,开孔腹板上、下T截面分别受到剪力Vt,Vb和剪力次弯矩Mt,Mb的共同作用,正应力分布如图 14(b)所示,假定剪力沿腹板均匀分布,钢腹板在正应力σw和剪应力τw共同作用下达到屈服,符合Von Mises屈服准则,即:
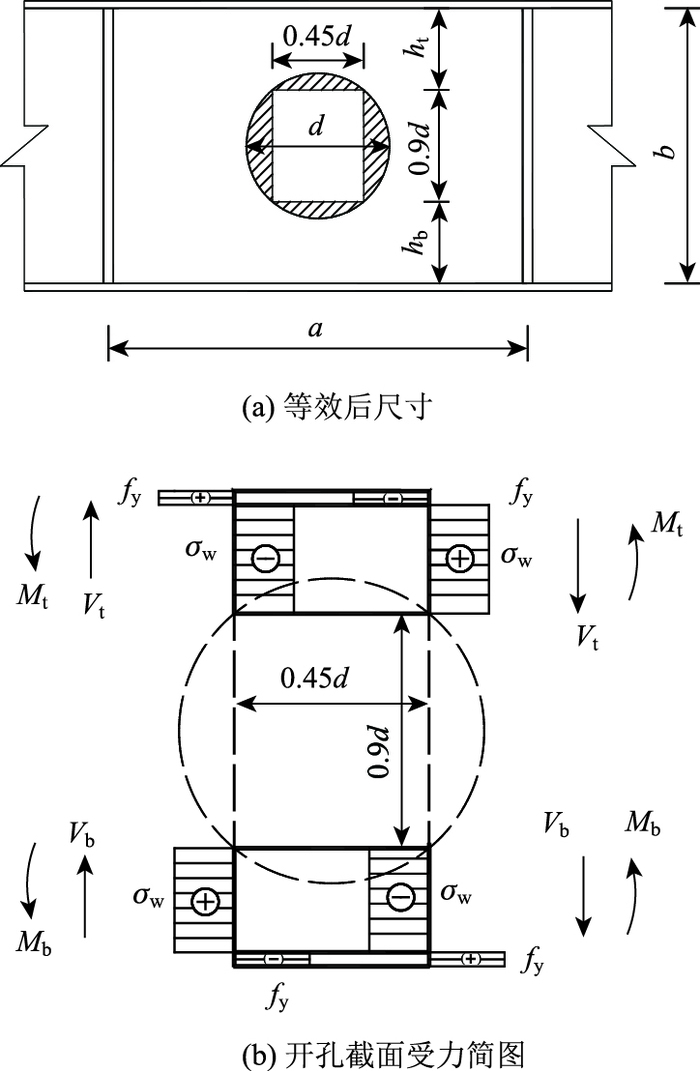
|
| 图 14 Vp计算示意图 Fig. 14 Schematic diagram for calculating Vp |
| |
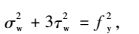
|
(11) |
式中fy为钢腹板的屈服强度。
认为上下翼缘板尺寸相对于腹板为小量,则对于下T截面,τwb=Vb/(hbtw),对下翼缘取矩可得:
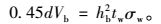
|
(12) |
联立式(11)、(12) 可得:
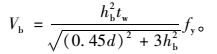
|
(13) |
同样的,对上T截面,亦有:
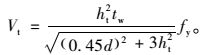
|
(14) |
若孔洞在腹板上无偏心,即ht=hb=h,则开孔腹板塑性抗剪强度为:
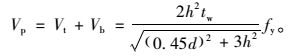
|
(15) |
定义开孔腹板的竖向开孔率为γ,由图 14可知, γ=0.9d/b,则γ′=1-γ为开孔截面处未削弱部分与整个截面的比率。
令Vcrel=Vpl,代入式(11) 和式(15),可得:
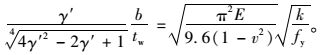
|
(16) |
将各材料参数代入式(16),有:
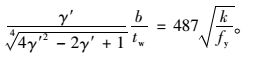
|
(17) |
令Vcrin=Vp,代入式(9) 和式(15),可得:
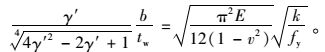
|
(18) |
将各材料参数代入式(18),有:
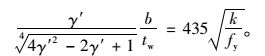
|
(19) |
由表 2~表 5可以看出,开孔腹板的屈曲后强度与其塑性极限荷载和弹性屈曲荷载的差值存在一定的比例关系,由各表计算结果可以偏安全地取比例系数为0.3,即有如下关系:
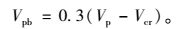
|
(20) |
开孔腹板的抗剪承载能力Vu为:
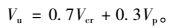
|
(21) |
定义参数υ为开孔腹板弹性屈曲强度与塑性强度的比值,即υ=Vcr/Vp,则式(21) 可写为:
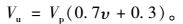
|
(22) |
当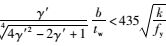
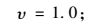
|
当
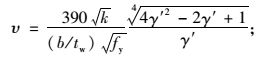
|
当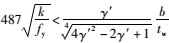
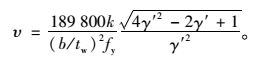
|
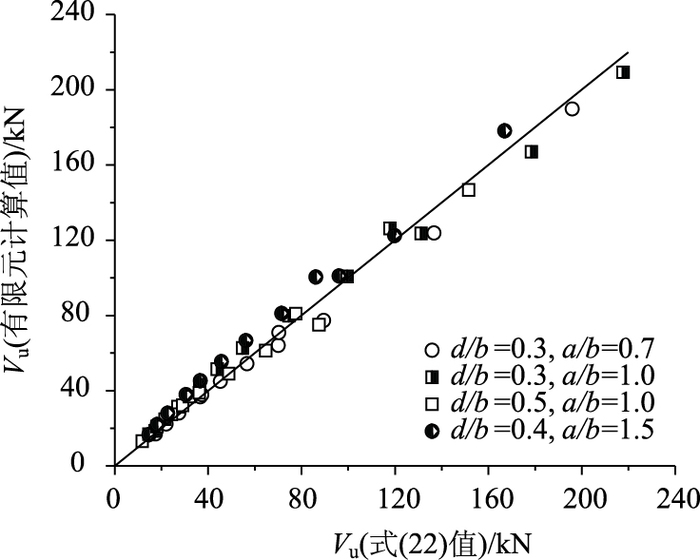
图 15给出了式(22) 计算值与有限元计算值的比较,从图可以看出,式(22) 与有限元结果较为吻合,且大部分计算结果偏安全。
|
| 图 15 式(22) 与FEM计算结果比较 Fig. 15 Comparison between calculation results by eq. 22 and FEM |
| |
2.3 初始几何缺陷的影响
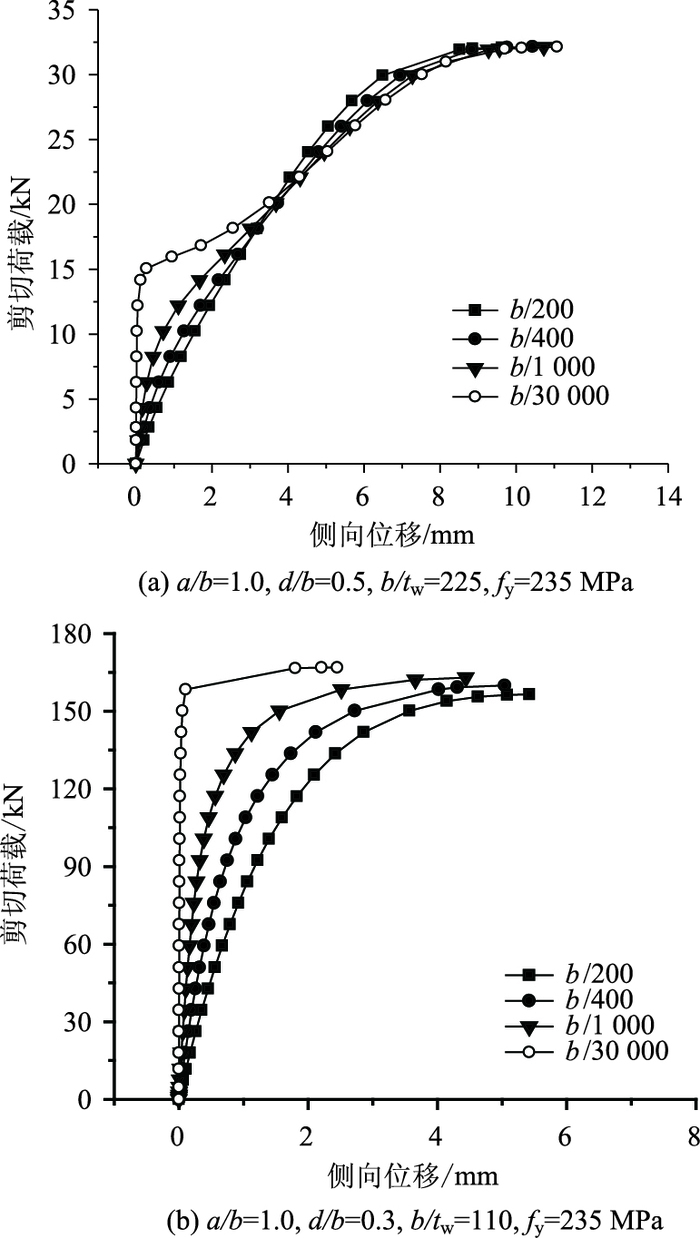
前述计算中,开孔板的初始几何缺陷取值很小,均为b/30 000,可认为无几何缺陷,为考察初始几何缺陷对开孔板抗剪承载能力的影响,对模型施加不同的初始几何缺陷进行计算,分析模型的几何尺寸和材料参数与2.2节一致,初始几何缺陷幅值逐级取为b/30 000,b/1 000,b/400,b/200。不同初始几何缺陷下的荷载-侧移曲线(P-δ)如图 16所示,横坐标取腹板最大侧向位移点处的平面外位移。
|
| 图 16 不同初始几何缺陷时的荷载-位移曲线 Fig. 16 Load-displacement curves with different initial geometrical imperfections |
| |
由图 16可知,对腹板高厚比相对较大的模型,不同初始几何缺陷对曲线的形式有较大影响,而极限荷载相差很小, 如图 16(a)所示;腹板高厚比相对较小时,开孔腹板的抗剪承载力会随着初始几何缺陷的增大而有一定的减小,但幅值不大,如图 16(b)所示, 初始几何缺陷为b/30 000和b/200时,相应的极限荷载分别为166.9,156.5 kN,下降约6.2。综上所述,初始几何缺陷对开孔腹板的抗剪承载能力影响较小。
3 结论(1) 各种边界条件下的开孔腹板,其屈曲模态表明,在剪力作用下开孔腹板均在孔洞边缘发生局部屈曲,该区域是组合蜂窝梁受力的薄弱环节,在设计中应予以加强。
(2) 通过大量的有限元数值分析,得到了不同边界条件下开孔腹板的剪切屈曲系数计算公式,公式具有较高的精度,可用于开孔腹板的剪切屈曲计算。
(3) 开孔腹板由于孔洞的存在,屈曲后拉力场被破坏,但仍可发展一部分屈曲后强度,其极限抗剪承载力可表示为弹性屈曲强度与屈曲后强度之和,屈曲后强度可表示为开孔腹板塑性强度的30%,对比验证表明,该计算方法与有限元计算结果基本吻合,且总体偏于安全,能够满足工程精度的要求。
(4) 不同的初始几何缺陷对开孔腹板荷载-位移曲线形式有较大影响,但对其抗剪承载能力影响很小。
| [1] | 湖南大学桥梁研究所. 钢-混凝土组合蜂窝连续梁桥方案设计(首创桥型)[R]. 长沙: 湖南大学, 2008. Bridge Engineering Institute of Hunan University. Scheme Design for Steel-concrete Composite Continuous Castellated Beam (Originated Bridge-type)[R]. Changsha:Hunan University, 2008. |
| [2] | 王皓磊, 邵旭东, 刘春. 带加劲肋钢-混凝土组合蜂窝梁承载能力试验[J]. 中国公路学报, 2013, 26(2): 110-118 WANG Hao-lei, SHAO Xu-dong, LIU Chun. Experiment on Bearing Capacity of Steel-concrete Composite Castellated Beams with Reinforced Rib[J]. China Journal of Highway and Transport, 2013, 26(2): 110-118 |
| [3] | 苏益声, 王良才. 圆孔蜂窝梁及其强度计算[J]. 广西大学学报:自然科学版, 1993, 18(3): 63-69 SU Yi-sheng, WANG Liang-cai. The Strength Calculation of the Circular Hole Castellated Beam[J]. Journal of Guangxi University:Natural Sciences Edition, 1993, 18(3): 63-69 |
| [4] | 邹锦华, 魏德敏, 苏益声, 等. 蜂窝梁的简化计算及其试验对比[J]. 华南理工大学学报, 2005, 33(1): 47-51 ZOU Jin-hua, WEI De-min, SU Yi-sheng, et al. Reduced Calculation and Its Experimental Comparison for Castellated Beams[J]. Journal of South China University of Technology, 2005, 33(1): 47-51 |
| [5] | 邵旭东, 刘俊珂. 计入加劲肋的圆孔蜂窝组合梁强度简化计算[J]. 湖南大学学报:自然科学版, 2009, 36(9): 7-11 SHAO Xu-dong, LIU Jun-ke. Reduced Reduced Computation of the Strength of Circular Hole Castellated Composite Beams with Stiffened Webs[J]. Journal of Hunan University:Natural Sciences Edition, 2009, 36(9): 7-11 |
| [6] | ZAAROUR W. Web Buckling in Thin Webbed Castellated Beams[J]. Journal of Structural Engineering, 1995, 122(8): 860-866 |
| [7] | DEMIRDJIAN S, REDWOOD R. Castellated Beam Web Buckling in Shear[J]. Journal of Structural Engineering, 1998, 124(10): 1202-1207 |
| [8] | DEMIRDJIAN S. Stability of Castellated Beam Webs[D]. Montreal:McGill University, 1999. |
| [9] | BASLER K. Strength of Plate Girders in Shear[J]. Journal of Structural Division, 1961, 128(7): 151-180 |
| [10] | BASLER K. Strength of Plate Girders under Combined Bending and Shear[J]. Journal of Structural Division, 1961, 87(7): 181-197 |
| [11] | GB 50017-2003, 钢结构设计规范[S]. GB 50017-2003, Code for Design of Steel Structure[S]. |
| [12] | American Institute of Steel Construction. Load and Resistance Factor Design Specification, for Structural Steel Buildings[S]. Chicago:AISC, 1999. |
| [13] | 陈骥. 钢结构稳定理论与设计[M]. 北京: 科学出版社, 2003: 1-25. CHEN Ji. Stability of Steel Structures Theory and Design[M]. Beijing: Science Press, 2003: 1-25. |
| [14] | 任涛. 工字梁腹板在局部承压和剪力作用下的弹性屈曲及极限承载力[D]. 杭州: 浙江大学, 2005. REN Tao. Elastic Buckling and Ultimate Strength of Web Plates in Ⅰ-girders under Patch Loading and Shear[D]. Hangzhou:Zhejiang University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10335-2005086976.htm |
| [15] | LEE S C, DAVIDSON J S, YOO C H. Shear Buckling Coefficients of Plate Girder Web Panels[J]. Computers and Structures, 1996, 59(5): 789-795 |
| [16] | LEE S C, YOO C H. Strength of Plate Girder Web Panels under Pure Shear[J]. Journal of Structural Engineering, 1998, 125(2): 184-194 |
| [17] | LAWSON R M, LIM J, HICKS S J, et al. Design of Composite Asymmetric Cellular Beams and Beams with Large Web Openings[J]. Journal of Constructional Steel Research, 2006, 62(6): 614-629 |
| [18] | CHUNG K F, LAWSON R M. Simplified Design of Composite Beams with Large Web Openings to Eurocode 4[J]. Journal of Constructional Steel Research, 2001, 57(2): 135-164 |
 2017, Vol. 34
2017, Vol. 34
