扩展功能
文章信息
- 唐亮, 凌立鹏, 高原
- TANG Liang, LING Li-peng, GAO Yuan
- 基于轮式滚动加载的正交异性钢桥面板疲劳试验设计
- Design of Fatigue Test for Orthotropic Steel Deck Based on Wheel Running Loading
- 公路交通科技, 2017, 34(8): 57-65, 75
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(8): 57-65, 75
- 10.3969/j.issn.1002-0268.2017.08.009
-
文章历史
- 收稿日期: 2016-06-20
2. 中交公路长大桥建设国家工程研究中心有限公司, 北京 100088
2. CCCC Highway Bridges National Engineering Research Centre CO., Ltd., Beijing 100088, China
自20世纪50年代问世以来,正交异性钢桥面板(下面简称“钢桥面板”)凭借重量轻、承载能力强、施工速度快的优势,成为国内外大中跨度钢桥广泛采用的桥面结构形式。然而由于钢桥面板直接承受车辆轮荷载的反复作用,且焊接构造及应力状况复杂,导致钢桥面板疲劳问题十分突出,自英国Severn桥渡(1966年建成通车)于1971年首先发现钢桥面板疲劳裂纹以来,各国均出现了大量的钢桥面板疲劳开裂事例,目前仍没有很好的解决办法[1-4]。钢桥面板的疲劳问题已成为影响钢桥安全及耐久运营的突出问题之一。
究其原因,除车辆超载、制造施工质量差、沥青桥面铺装易损等因素外,钢桥面板自身抗疲劳设计方法的不完善,特别是各构造接头疲劳强度试验确定方法的不完善也是重要原因。
英国Severn桥渡发现钢桥面板疲劳裂纹后,为了改进结构的功效和为钢桥面板的疲劳设计提供指导原则,在ECSC(European Coal and Steel Community,欧洲煤钢共同体)的长期资助下,德国、比利时、法国、意大利、荷兰和英国等国研究中心开展了长达30 a的“Measurement and interpretation of dynamic loads in bridges”专项联合攻关,在钢桥面板疲劳荷载及应力反应、主要构造的疲劳抗力及优化等方面进行了大量的实桥测试及室内模型疲劳试验,建立了目前世界上最完整、最系统的钢桥面板各构造焊接接头的疲劳试验数据库[5],欧洲规范Eurocode[6-7]、美国规范AASHTO LRFD[8]等均是以此为基础制订了有关正交异性钢桥面板的相关条款。此外,美国、日本、中国也结合国内钢桥面板使用及疲劳病害情况开展了有针对性的研究[9-16],进一步规范了钢桥面板的设计和制造。
从试验方法上看,由于受试验装备水平及经费所限,早期欧洲进行的钢桥面板构造细节疲劳试验基本均采用小型试件,见图 1,相比实际桥面结构,由于边界约束不足,小型试件中可引入的残余应力非常有限;此外,在疲劳加载方式上,欧洲进行的试验基本均为固定点加载,无法模拟车辆荷载通过时在钢桥面板各构造细节处产生的非成比例的多轴疲劳效应。这些因素均造成疲劳试验结果偏于乐观。
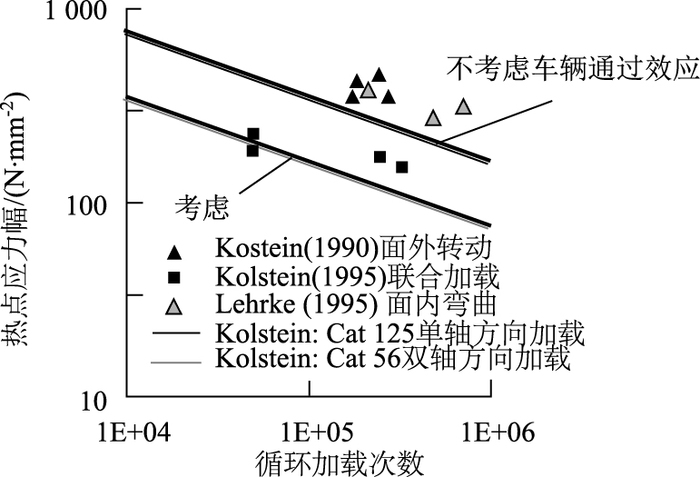
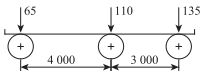
部分试验研究已经表明[18],车辆荷载通过效应对桥面板疲劳性能影响显著。如对于钢桥面板U肋-横隔板连接接头的U肋壁板水平裂纹C.6(见图 2),在不考虑车辆通过效应的情况下,试验测试的疲劳强度可以达到欧洲规范125级,但考虑后试验测试结果只能达到欧洲规范56级,疲劳抗力大大降低,如图 3所示。
|
| 图 2 U肋与横隔板连接处的裂纹类型 Fig. 2 Crack patterns near U-rib-to-diaphragm joints |
| |
能模拟车辆荷载通过效应的加载装置是研究钢桥面板等桥面结构疲劳性能的核心设备,加载长度短、加载速率快的轮荷重走行试验机还没有定型产品,只有日本个别研究单位有几台。利用国内首台自主研发的桥面结构专用轮式滚动疲劳加载装置,以广东虎门二桥坭洲水道桥为依托工程,研究基于轮式滚动加载的正交异性钢桥面板疲劳试验设计问题。
1 专用轮式滚动疲劳加载装置简介为攻克车辆荷载通过效应模拟加载技术难题,满足桥面结构疲劳试验高次数、大轮载、高频率、低成本的要求,公路长大桥建设国家工程研究中心自主研发了国内首台桥面结构用轮式滚动疲劳加载装置,见图 4。国内外现有类似设备指标对比情况见表 1。

|
| 图 4 轮式滚动疲劳加载装置 Fig. 4 Wheel running fatigue loading equipment |
| |
| 使用单位 | 最大 轮载 /kN | 加载 频率/ (往复· min-1) | 加载 长度/m | 试件最大尺寸 (宽×长×高) /m3 |
| 日本土木研究所 | 490 | 34.7 | ±0.5~±1.5 | 3×4.5×0.35 |
| 高速道路総合技術研究所 | 490 | 30 | ±1.5 | 7×15×(1.5~4) |
| 横河ブリッジ | 196 | 17 | ±1.0 | 4.8×12×(1.2~1.7) |
| 石川島播磨重工業 | 490 | 30 | ±0.5~±1.5 | 5.3×4.5×0.35 |
| 大阪大学 | 294 | 28 | ±1.0 | 2×3 |
| G & U技術研究センター | 200 | — | ±2.25 | 1.5×3×0.4 |
| 寒地土木研究所 | 300 | 24 | ±1.0 | — |
| 公路长大桥国家中心 | 490 | 35 | ±0.5~±2.0 | 5×12×1.5 |
该系统采用伺服作动器对行走单元施加垂直载荷,同时通过变频电机驱动行走单元作水平方向的往复运动,可连续无间断对桥面试件进行动载测试。系统主要由竖向加载系统、行走导向系统、反力支撑系统、行走单元及其他辅助机构组成,主要特点如下:
(1) 竖向加载系统为电液伺服系统,负责行走单元对结构试件进行加载,载荷在0~500 kN范围内无级可调,加载模式可为恒力载荷、正弦波、方波、斜波、三角波、随机波等,加载频率可达3 Hz,加载精度为±2.0%;此外行走单元可为橡胶轮或钢轮,可形成单轴单轮组、单轴双轮组、双轴双轮组。因此,实现了多种轮载加载模式和组合样式,而且加载频率高、精度高、轮载大。
(2) 行走导向系统为电机驱动系统,通过曲柄连杆机构负责驱动行走单元水平往复运动,行走单元运动频率不低于35往复/min,在试件长度方向作用行程±2.0 m,具有运动频率高、加载范围大的优点。
(3) 反力支撑系统设垂直升降机构和水平移位机构,使行走单元可在试件宽度方向±1 m范围内、在试件竖直方向距地面1.0~2.5 m范围内任意位置自锁;另外地面设置了18 m长×6 m宽的反力槽道。因此,实现了行走单元对试件长、宽、高3个方向宽范围的加载能力。
(4) 本系统适用于桥面结构、桥面(或路面)铺装结构、桥梁伸缩装置等多种结构,适用范围广,而且便于使用和维修、经济性好。
专用轮式滚动疲劳加载装置的成功研制,对增强我国钢桥抗疲劳技术研发能力,形成具有自主知识产权的桥面系耐久保障技术及产品,提升我国钢桥建造和养护维修技术水平,降低桥梁全寿命周期成本具有十分积极的促进作用。
2 模型结构设计 2.1 虎门二桥钢箱梁节段有限元模型本文以广东虎门二桥坭洲水道桥钢箱梁节段为参考模型进行分析,该结构在我国采用很多,具有广泛的代表性。
虎门二桥坭洲水道桥为主跨1 688 m双塔双跨悬索桥,跨径布置为(658+1 688+522) m。矢跨比为1:9.5,主缆横桥向中心间距为42.1 m,吊索顺桥向标准间距为12.8 m。钢箱梁梁高4 m;标准梁段长12.8 m,设置四道实腹式横隔板,间距3.2 m;顶板U肋上口宽300 mm,下口宽170 mm,高280 mm,U肋中心距600 mm;底板U肋上口宽240 mm,下口宽500 mm,高260 mm,U肋中心距1 000 mm。顶板在外侧重车道厚18 mm,内侧快车道厚16 mm,U肋板厚8 mm,底板厚10 mm,斜底板厚10 mm,底板U肋板厚6 mm;标准横隔板厚10 mm,吊索处增加为14 mm。
计算中以标准梁段为对象进行分析。为降低计算规模,采用了如图 5所示的一半结构模型。该模型在纵桥向为包括5个横隔板的4跨结构,模型两端横隔板为吊索处的横隔板。

|
| 图 5 扁平钢箱梁节段模型 Fig. 5 Segmental model of flat steel box girder |
| |
为尽可能反映钢桥面板在实际结构中的受力特点,有限元模型边界约束按如下方式施加:在道路中心线截面采用X向对称约束;在端横隔板截面,约束钢箱及纵肋的纵向(Z向)平动自由度及绕竖轴(Y向)和横轴(X向)的转动自由度,以近似反映端横隔板为桥跨内的横隔板,而不是边界上的支承横隔板;在端横隔板截面,约束钢箱腹板的竖向(Y向)平动自由度,以近似反映斜拉索的约束作用。根据Saint-Venant原理,采用上述边界条件,只要距边界一定距离,则与实桥中的钢桥面板受力不会产生较大偏差。
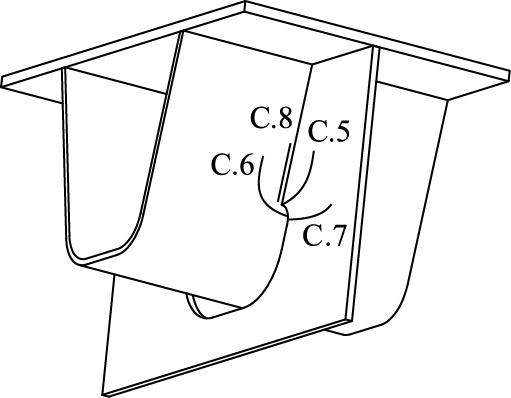
参考《公路桥涵设计通用规范》(JTG D60—2015) 中的车辆轴载样式进行加载,加载分为双轮轴载和单轮轴载两种,轮距1 800 mm,其中双轮轴重140 kN,双轮着地宽度和长度为600 mm×200 mm;单轮轴重30 kN,单轮着地宽度和长度为300 mm×200 mm,如图 6所示。未考虑桥面铺装层的荷载分布作用。
|
| 图 6 轴载样式(单位:mm) Fig. 6 Patterns of axle loads(unit:mm) |
| |
根据行车道划分及结构特点,分析中关注横隔板为+Z方向第3道横隔板,关注U肋为从桥梁中心线开始计的第4个U肋,其位于内侧快车道,见图 5。轴载在纵桥向可以移动,相对于关注横隔板,包括轴载纵向位置LLWL=-6 400,3 200,…,0,…,3 200,6 400 mm等位置,其中Z=-3 200,0,3 200 mm分别为+Z方向第2,3,4道横隔板位置。
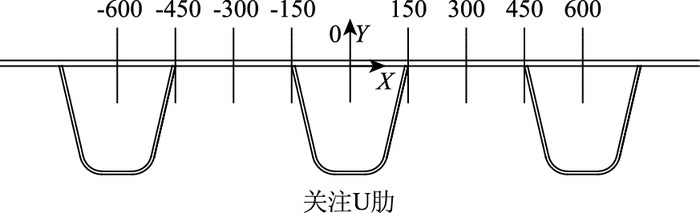
轴载在横桥向参考行车道划分进行布置:轴载在横桥向布置于内侧快车道,一侧车轮中心相对于关注U肋按如图 7所示的方式布置,包括轴载横向位置TLWL=-600,-450,…,0,…,450,600 mm等位置。
|
| 图 7 轴载横向位置(单位:mm) Fig. 7 Transverse positions of axle loads(unit:mm) |
| |
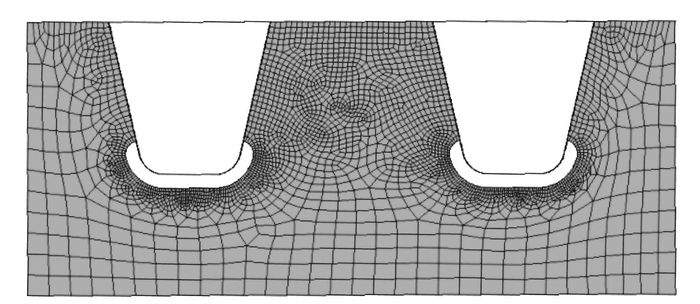
采用壳单元对结构剖分,计算在通用有限元程序ANSYS平台上进行。所用单元类型为8节点曲壳单元SHELL93,在所关心截面附近,有限元网格尺寸减小为4 mm,局部有限元网格划分见图 8。单元尺寸敏感性测试表明,对于所用的单元类型,U肋与横隔板相交处附近单元尺寸由10 mm减小为4 mm,对计算结果影响在1%以内,已收敛。
|
| 图 8 局部有限元网格 Fig. 8 Local FE mesh |
| |
2.2 试验模型选取
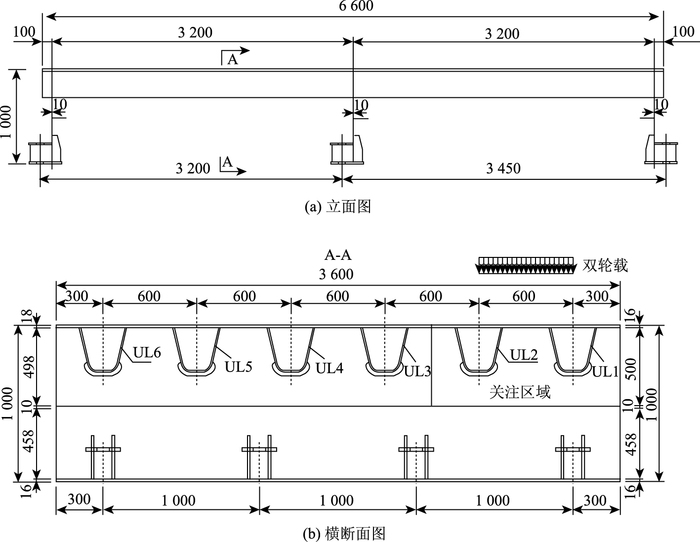
为获得钢箱梁桥面系统各连接处附近实际的应力分布,同时有效控制试件的规模和加载吨位,以虎门二桥标准梁段为对象,初步设计了如图 9所示试验模型:纵桥向采用了(3.2+3.2) m的纵向2跨结构,横桥向包括6个U肋。顶板厚16 mm和18 mm,U肋厚8 mm,横梁腹板厚10 mm,其他主要尺寸与虎门二桥相同。
|
| 图 9 模型尺寸(单位:mm) Fig. 9 Model dimensions(unit:mm) |
| |
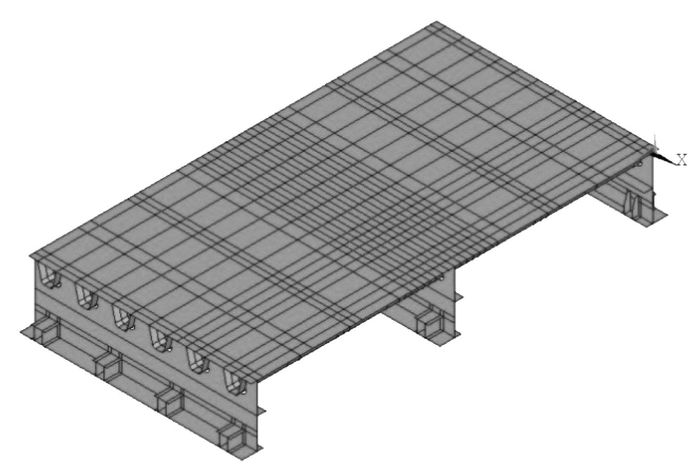
根据图 9所示的试验模型,建立了如图 10所示的有限元模型。计算中约束所有横梁下翼缘和锚箱上翼缘自由度。
|
| 图 10 计算模型 Fig. 10 Calculated model |
| |
分析中关注横隔板取中间横隔板,关注U肋取靠自由边外侧2个U肋,如图 9所示。加载采用双轮载,轮重70 kN,双轮胎着地宽度和长度为600 mm×200 mm,不考虑桥面铺装层的荷载分布作用。轮载在横向布置于相邻关注U肋中心,如图 9所示;轮载在纵桥向可以移动,相对于关注横梁,包括LLWL=-3 200,-1 600,…,0,…,1 600,3 200 mm等位置,其中LLWL=-3 200,0,3 200 mm分别为+Z方向第1,2,3道横隔板位置。
2.3 计算结果对比分析在对钢箱梁节段模型和试验模型计算结果对比的过程中,关注的疲劳敏感部位热点包括横隔板弧形切口周边热点FB、U肋与横隔板连接焊缝端部热点RF、顶板与U肋连接焊缝端部热点RD、U肋-横隔板-顶板三者相交处热点RDF,如图 11所示。
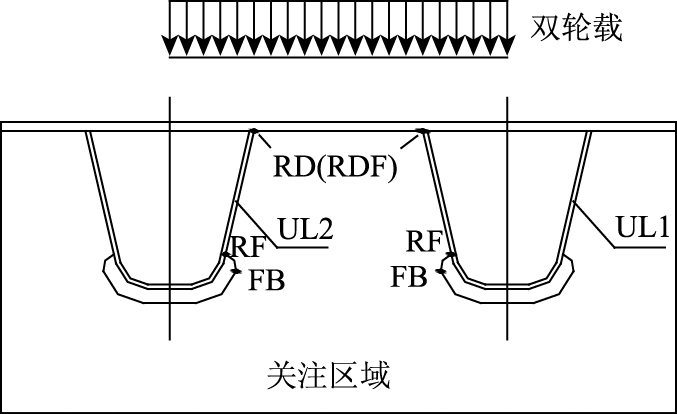
|
| 图 11 疲劳敏感部位热点位置 Fig. 11 Positions of hot points near fatigue-prone details |
| |
重点关注的疲劳裂纹类型及其控制应力如下:
(1) 横隔板弧形切口周边热点FB的裂纹C.7,其控制应力为横隔板表面切向应力St’_top;
(2) 横隔板弧形切口端部热点RF的裂纹C.5,其控制应力为横隔板表面切向应力St’_top;
(3) U肋壁板热点RF的水平裂纹C.6,其控制应力为U肋外表面切向应力St_top;
(4) U肋壁板热点RF的竖向裂纹C.8,其控制应力为U肋外表面纵向应力Sz_top;
(5) 横隔板处顶板热点RDF的裂纹DPS01,其控制应力为顶板下表面横向应力Sx_bot;
(6) 顶板热点RD处的裂纹C.1和C.2,其控制应力为顶板下表面横向应力Sx_bot;
(7) U肋壁板裂纹C.3,其控制应力为U肋外表面切向应力St_top;
(8) 焊缝裂纹C.4,其控制应力为U肋内表面切向应力St_bot。
其中(1)~(5) 为U肋与横隔板交叉部位的裂纹形式,(6)~(8) 为顶板与U肋交叉部位的裂纹形式,如图 2和图 12所示。
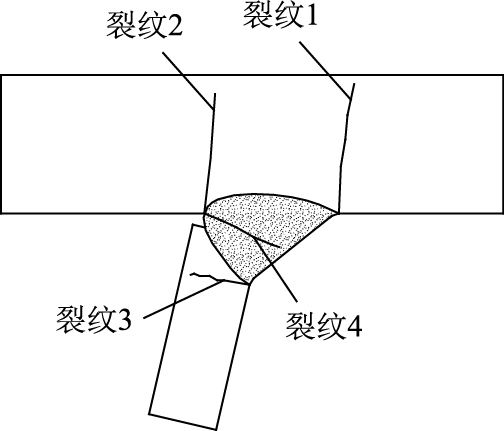
|
| 图 12 顶板与U肋连接处的裂纹类型 Fig. 12 Crack patterns near deckplate-to-U-rib joint |
| |
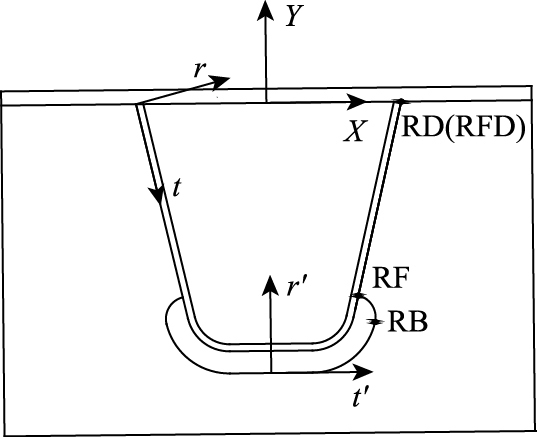
为方便起见,分析中所用局部坐标系如图 13所示:
|
| 图 13 局部坐标系定义 Fig. 13 Definition of local coordinate system |
| |
(1) X-Y直角坐标系,坐标原点位于U肋中心,用于描述顶板应力状态;
(2) t-r曲线坐标系,坐标原点位于U肋底部中心,用于描述U肋应力状态;
(3) t′-r′曲线坐标系,坐标原点位于横隔板弧形切口底部中心,用于描述横隔板弧形切口的应力状态。
计算结果表明:采用双轮载横向布置于外侧两U肋中心的加载模式,外侧两U肋附近,特别是轮载直接作用下的构造细节可有效加载;对于横隔板弧形切口周边热点FB、U肋与横隔板连接焊缝端部热点RF、顶板与U肋连接焊缝端部热点RD、U肋-横隔板-顶板三者相交处热点RDF等疲劳敏感部位热点,试验模型外侧两U肋在热点附近的应力状态与钢箱梁节段模型基本相同,试验模型结构形式和边界条件是合理的。
图 14给出了UL1肋壁板热点RF应力影响线。UL2肋和其他裂纹控制应力也有类似的结果。
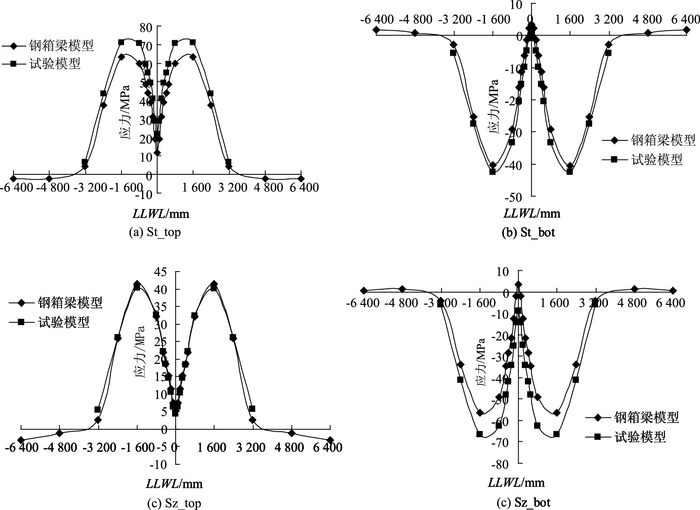
|
| 图 14 UL1肋壁板热点RF应力影响线 Fig. 14 Influence lines of stresses at hot point RF in web of rib UL1 |
| |
3 轮式滚动试验疲劳荷载分析
为试验验证虎门二桥钢桥面板各疲劳易损部位设计寿命期内的抗疲劳安全性,还需通过疲劳累积损伤理论合理确定试验疲劳荷载方案。主要研究过程如下:
(1) 根据《广东虎门二桥工可研究阶段公路桥梁车辆荷载专题研究》,并考虑我国车辆荷载现状及发展趋势,确定实桥疲劳荷载谱,包括5种车型,见表 2。
(2) 利用虎门二桥钢箱梁节段有限元模型,计算实桥钢桥面板在典型双轮轴载和单轮轴载作用下疲劳敏感部位的应力影响面。图 15给出了在双轮轴载下的U肋壁板热点RF应力St_top影响面。对于其他疲劳裂纹控制应力也可计算得到类似的结果。
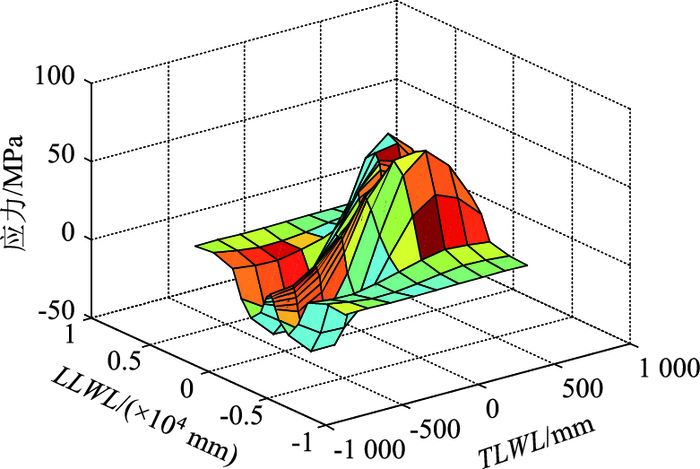
|
| 图 15 U肋壁板热点RF应力St_top影响面 Fig. 15 Stress influence surface of St_top at hot point RF in web of U-rib |
| |
(3) 计算实桥钢桥面板各细节控制应力在不同车型作用下的应力历程,包括如图 7所示的9种轮载横向位置。图 16给出了在设计疲劳荷载谱各车型作用下,轴载横向位置TLWL=300 mm时的U肋壁板热点RF应力St_top历程。
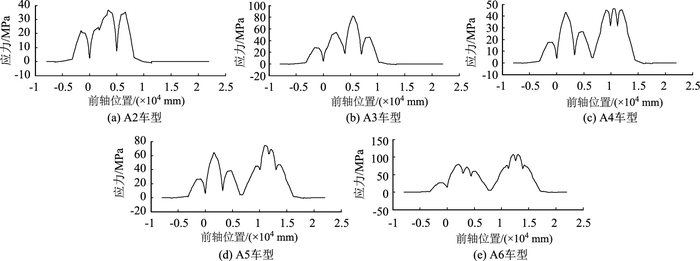
|
| 图 16 U肋壁板热点RF应力St_top历程 Fig. 16 Stress histories of St_top at hot point RF in web of U-rib |
| |
采用雨流计数法计算应力谱,根据Miner疲劳损伤累积理论转化为每种车型通过1次的等效应力幅,按下式计算:
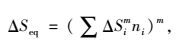
|
(1) |
式中,ΔSi和ni分别为每种车型通过1次所产生的应力幅及作用次数,由雨流计数法计算得到;m为该构造细节S-N曲线斜率的负倒数,对于焊接结构一般取3。
在此基础上,结合交通量预测计算实桥各构造细节在设计寿命期内的疲劳累积损伤,按式(2) 计算:
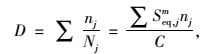
|
(2) |
式中,ΔSeq, jm为第j种车型通过1次所产生的等效应力幅,按式计算;nj为在设计寿命期内第j种车型的交通量;C为该构造细节S-N曲线特征常数。
(4) 根据专用轮式滚动疲劳加载装置性能参数,分别计算橡胶轮双轴加载和钢轮单轴加载下试验模型各细节的应力历程;然后计算试验模型各细节在试验轴载通过1次所产生的等效应力幅ΔSeqt,由疲劳累积损伤等效可得:
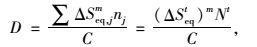
|
(3) |
式中,Nt为试验轴载累计作用次数。
由式(3) 整理可得:
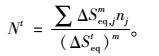
|
(4) |
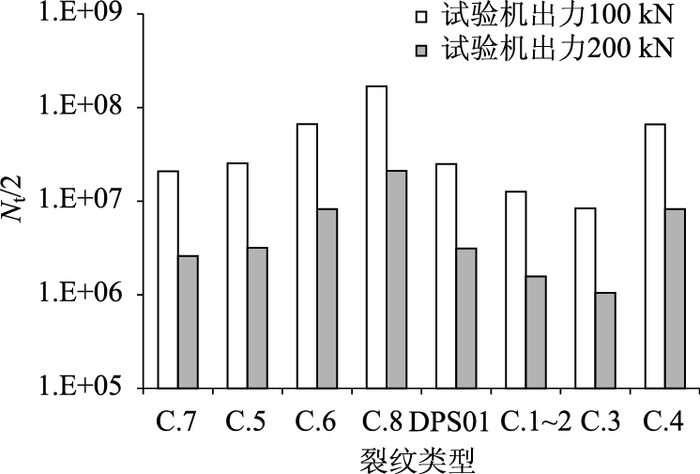
由此,可计算试验模型在双轴荷载作用下各构造细节的等效作用次数,见图 17。根据专用轮式滚动疲劳加载装置的性能指标,采用橡胶轮双轴加载,双轴间距1.4 mm,纵向运动范围±2 m,为避免在高轮载作用下橡胶轮出现爆胎,试验机最大出力200 kN。由图可见,在此荷载水平下,为检验主要构造细节在设计寿命期内的疲劳耐久性,试验轮载往复作用次数(Nt/2) 最大需达到2 000万次以上(对应U肋壁板热点RF的竖向裂纹C.8),即使对于经常出现的U肋壁板热点RF的水平裂纹C.6,往复作用次数也需要达到800万次以上,试验时间过于漫长。
|
| 图 17 双轴荷载等效作用次数 Fig. 17 Equivalent loading numbers of dual-axle load |
| |
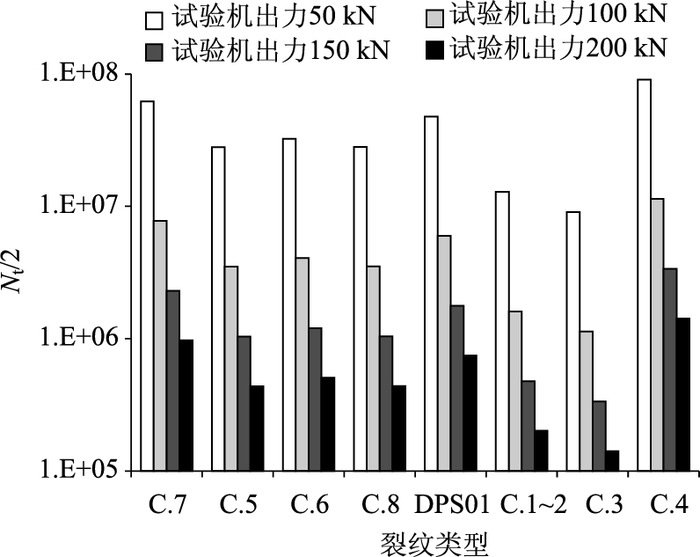
对于单轴加载的情况,可以采用钢轮,试验机最大出力可达500 kN。图 18给出了试验模型在单轴荷载作用下各构造细节的等效作用次数。由图可见,在试验机出力150 kN荷载水平下,试验轮载往复作用次数最大337万次(对应顶板与U肋间的焊缝裂纹C.4),与橡胶轮双轴加载相比,试验次数大大减少;当试验机出力200 kN时,试验轮载往复作用次数只需142万次。考虑到试验时间成本、实际轴载水平、业内习惯等因素,因此确定本试验采用钢轮单轴加载,试验机出力200 kN。
|
| 图 18 单轴荷载等效作用次数 Fig. 18 Equivalent loading numbers of single-axle load |
| |
需要指出的是,采用Miner疲劳损伤累积理论,在试验轮载往复运动的一个周期,单方向施加轮载(即滚轮向一侧运动时施加轮载,滚轮向另一侧运动时空载)对各构造细节引起的疲劳损伤刚好等于双方向施加轮载(即滚轮在往复运动中始终施加轮载)效应的一半,这表明采用Miner疲劳损伤累积理论并不能区别轮载施加方向的影响,这个问题还需要更多的试验研究。
4 试验加载规则基于轮式滚动加载的正交异性钢桥面板疲劳试验可分三阶段进行加载:
第一阶段:静载工况。采用轮式滚动疲劳加载装置进行慢速加载,以获得各主要疲劳易损部位的应力影响线,建立荷载作用与效应的对应关系,研究控制疲劳裂纹萌生和发展的关键点应力历程及受力机理。
第二阶段:设计寿命期疲劳性能验证试验工况。通过与实桥钢桥面板各细节的疲劳累计损伤等效,确定试验加载轴类型、加载水平以及对应各细节的等效作用次数;以此为参照,开展轮式滚动疲劳加载,以验证实桥钢桥面板各细节设计寿命期内的抗疲劳安全性。
第三阶段:破坏性疲劳强度试验工况。第二阶段试验完成后,根据试验进行情况,采用原荷载或增大荷载继续轮式滚动疲劳加载,获得典型疲劳易损部位的疲劳强度。
在测试方案中,除横隔板开孔周围测点采用距离开孔边缘5 mm布置外,其余测点均按距离焊趾10 mm进行布置,一方面可以有效避免焊接结构温度应力、几何尺寸等带来的影响,另一方面便于与基于热点应力法的精细实体有限元分析进行相互校正,如图 19所示。

|
| 图 19 测点位置 Fig. 19 Measuring point position |
| |
在整个试验过程中,每加载25万次将停机进行静载试验,采集测点应变数据并考察其变化是否异常,试验次数超过100万次后每加载50万次,依据《焊缝无损检测磁粉检测》(GB/T 26951—2011) 和《焊缝无损检测超声检测技术、检测等级和评定》(GB/T 11345—2013) 等进行1次磁粉和超声探伤,检查模型各关键部位是否出现开裂或异常。试件出现疲劳裂纹后,将持续监测裂纹发展过程。
5 结论本文利用国内首台自主研发的桥面结构专用轮式滚动疲劳加载装置,以广东虎门二桥坭洲水道桥为依托工程,研究了基于轮式滚动加载的正交异性钢桥面板疲劳试验设计问题。首先,根据实桥交通需求分析,合理确定实桥疲劳荷载谱;其次,计算实桥钢桥面板在疲劳荷载谱各车型作用下的应力历程,采用雨流计数法计算应力谱,根据Miner疲劳损伤累积理论转化为每种车型通过1次的等效应力幅,结合交通量预测计算实桥各构造细节在设计寿命期内的疲劳累积损伤;最后,根据专用轮式滚动疲劳加载装置性能参数,分别计算橡胶轮双轴加载和钢轮单轴加载下试验模型各细节的等效应力幅,通过与实桥钢桥面板各细节的疲劳累计损伤等效,从而确定试验加载轴类型、加载水平以及对应各细节的等效作用次数。研究成果对指导正交异性钢桥面板疲劳试验设计有重要参考意义。
| [1] | DE JONG F B P. Overview Fatigue Phenomenon in Orthotropic Bridge Decks in the Netherlands[C]//Proceedings Orthotropic Bridge Decks. Sacramento, US:ASCE, 2004:489-512. |
| [2] | WOLCHUK R. Lessons from Weld Cracks in Orthotropic Decks on Three European Bridges[J]. Journal of Structural Engineering, 1990, 116(1): 75-84 |
| [3] | WOLCHUK R. Steel Orthotropic Decks Development in the 1990s[J]. Transportation Research Record, 1999, 1688: 30-37 |
| [4] | JONG F B P D, KOLSTEIN M H, BIJLAARD F S K. Research Project TU Delft; Behavior Conventional Bridge Decks & Development of Renovation Techniques[C]//Proceedings Orthotropic Bridge Decks. Sacramento, USA, 2004:594-615. |
| [5] | KOLSTEIN M H. European Research on the Improvement of the Fatigue Resistance and Design of Steel Orthotropic Bridge Decks[C]//Proceedings Orthotropic Bridge Decks. Sacramento, US:ASCE, 2004:466-488. |
| [6] | EN 1993-1-9 Eurocode 3:Design of Steel Structures-Part 1-9:Fatigue[S]. |
| [7] | EN 1993-2 Eurocode 3:Design of Steel Structures-Part 2:Steel Bridges[S]. |
| [8] | AASHTO 2012. AASHTO LRFD Bridge Design Specifications[S]. |
| [9] | TSAKOPOULOS P A, FISHER J W. Full-scale Fatigue Tests of Steel Orthotropic Decks for the Williamsburg Bridge[J]. Journal of Bridge Engineering, 2003, 8(5): 323-333 |
| [10] | TSAKOPOULOS P A, FISHER J W. Full-scale Fatigue Tests of Steel Orthotropic Deck Panel for the Bronx-Whitestone Bridge Rehabilitation[J]. Bridge Structures, 2005, 1(1): 55-66 |
| [11] | CONNOR R J, FISHER J W. Consistent Approach to Calculating Stresses for Fatigue Design of Welded Rib-to-web Connections in Steel Orthotropic Bridge Decks[J]. Journal of Bridge Engineering, 2006, 11(5): 517-525 |
| [12] | SIM H B, UANG C M, SIKORSKY C. Effects of Fabrication Procedures on Fatigue Resistance of Welded Joints in Steel Orthotropic Decks[J]. Journal of Bridge Engineering, 2009, 14(5): 366-373 |
| [13] | CHOI J H, KIM D H. Stress Characteristics and Fatigue Crack Behaviour of the Longitudinal Rib-to-cross Beam Joints in an Orthotropic Steel Deck[J]. Advances in Structural Engineering, 2008, 11(2): 189-198 |
| [14] | XIAO Z G, YAMADA K, YA S, et al. Stress Analyses and Fatigue Evaluation of Rib-to-deck Joints in Steel Orthotropic Decks[J]. International Journal of Fatigue, 2008, 30(8): 1387-1397 |
| [15] | YA S, YAMADA K. Fatigue Durability Evaluation of Trough to Deck Plate Welded Joint of Orthotropic Steel Deck[J]. Structural Engineering and Earthquake Engineering, 2008, 25(2): 33-46 |
| [16] | 唐亮, 黄李骥, 刘高, 等. 正交异性钢桥面板足尺模型疲劳试验[J]. 土木工程学报, 2014, 47(3): 112-122 TANG Liang, HUANG Li-ji, LIU Gao, et al. Fatigue Experimental Study of a Full-scale Steel Orthotropic Deck Model[J]. China Civil Engineering Journal, 2014, 47(3): 112-122 |
| [17] | MADDOX S J. The Fatigue Behaviour of Trapezoidal Stiffener to Deck Plate Welds in Orthotropic Bridge Decks, Supplementary Report 96UC[R]. Berkshire, UK:Transport and Road Research Laboratory, 1974. |
| [18] | KOLSTEIN M H. Fatigue Classification of Welded Joints in Orthotropic Steel Bridge Decks[D]. Delft:Delft University of Technology, 2007. |
 2017, Vol. 34
2017, Vol. 34