扩展功能
文章信息
- 孙聪, 方四发, 尹华锋, 肖铭钊, 邓利明
- SUN Cong, FANG Si-fa, YIN Hua-feng, XIAO Ming-zhao, DENG Li-ming
- 基于等面积正多边形逼近形式的边坡上限有限元法
- Upper Bound FE Method for Slope Analysis Based on Equal Area Regular Polygon Approximation Form
- 公路交通科技, 2017, 34(8): 44-49
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(8): 44-49
- 10.3969/j.issn.1002-0268.2017.08.007
-
文章历史
- 收稿日期: 2015-12-02
2. 武汉市市政路桥有限公司, 湖北 武汉 430015
2. Wuhan Municipal Road and Bridge Co., Ltd., Wuhan Hubei 430015, China
边坡的稳定性分析一直是岩土工程领域重要的研究课题。目前常用的几类边坡稳定性分析方法有极限平衡法、强度折减有限元法和极限分析法。极限平衡法[1-3]虽然抓住了边坡稳定破坏的主要矛盾,但其为了使不静定问题转化成静定问题,引入了过多假设,且无法考虑应力-应变关系,把不确定性全部加在了条间力上,最终得到的解既不是上限解也不是下限解;强度折减有限元法可以弥补极限平衡法的各种不足,其理论体系更为严格,能够全面满足静力许可、应变协调和应力-应变本构关系,但是,目前对于边坡何时达到极限状态的判定标准还没有统一的结论[4-5],是以计算不收敛还是塑性区贯通为判据尚存争议。
事实上,工程中对于边坡最关心的问题是它是否稳定、安全程度如何以及潜在滑动面和破坏模式是什么样子,我们并不需要知道边坡每个高斯点的应力应变的具体量值是多少。对于此类问题,极限分析法为我们提供了很好的解决方案,从极大和极小值出发,运用下限法和上限法,分别放松边坡内力和位移的约束,从两个方向逼近极限解。由于速度场相对于应力场更容易构建,且极限分析上限法在得到边坡安全系数的同时,可以给出边坡的临界破坏模式,因此相较于下限法具有更广阔的应用空间。
塑性极限分析方法首创于20世纪20年代。Drucker、Prager、Greenberg等[6-7]把静力场和速度场结合起来提出了极值理论,建立了完整的塑性极限分析理论;Chen[8]将滑坡体视为刚塑性体,滑动面仅限于对数螺旋线,提出了一种用于求解二维边坡旋转破坏的上限解方法;陈祖煜等[9]以极限分析上限理论体系为基础,推出了基于斜条分思想的斜条分上限解法;Sloan等学者[10-11]将土力学中的极限分析与有限元法相结合,解决了数值极限分析法存在的一系列困难,为极限分析在大规模复杂条件下的工程应用打下了基础,此后的大部分学者在极限分析方面的研究均是沿着这一思路展开的。国内学者中,王均星[12]、殷建华[13]、杨峰[14-15]、高连生[16]等人均从不同角度对此进行过研究。
目前的上限有限元法中,对于摩尔库伦屈服圆的线性化全是基于外切多边形进行逼近,这种情况下,只有当多边形的边数p足够多时(一般p≥15),才能达到较好的收敛效果,这就大大增加了优化变量数,影响计算效率。其实,从本质上来看,只要所求的极限荷载是从上方收敛的,就是它的一个上限解,从这点出发,我们放松单元内任一点需严格满足上限性质的约束,采用等面积正多边形的形式来逼近摩尔库伦屈服圆,得到新的线性流动方程。虽然采用等面积正多边形逼近屈服圆时不满足任一点均位于屈服面外的上限要求,但这并不影响整体系统解的上限性质,且在较少的多边形边数时可达到较好的收敛效果。
1 上限法原理上限定理可以表述为:一个受力物体,在满足相容条件和速度边界条件的变形模式下,由虚功原理计算得到的荷载,不小于真实的破坏荷载,相应的速度场则被称为运动许可速度场。
上限定理就是在所有运动许可速度场下寻找的外荷载T的最小值。
为了方便起见,把外荷载T写成已知荷载T的倍数,也即λT, λ为比例因子,则上线定理变为一个等价的规划问题:

|
(1) |
对于平面应变问题,以拉应力为正,摩尔库伦屈服函数准则可表示为:
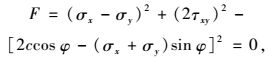
|
(2) |
式中,c和φ分别为黏聚力和摩擦角;σx, σy, τxy分别为不同方向的应力值;F为屈服函数。
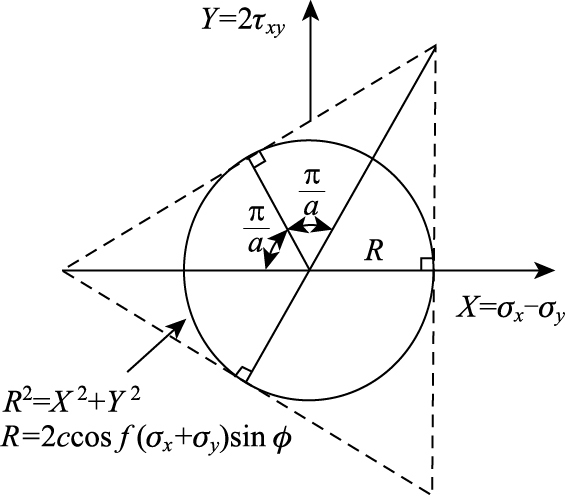
如果以σx-σy为X轴,2τxy为Y轴建立坐标系,那么式(2) 可以表达为一个圆,圆心位于原点,半径R为2ccosφ-(σx+σy)sin φ,如图 1所示,图中a为外切多边形边数。
|
| 图 1 外切多边形逼近摩尔库伦屈服圆(a=3) Fig. 1 Circumscribed polygon approximating Mohr-Coulomb yield circle |
| |
传统做法是利用外切多边形逼近来将上述屈服函数线性化[10],每条边的方程为:

|
(3) |
式中,

|
(4) |
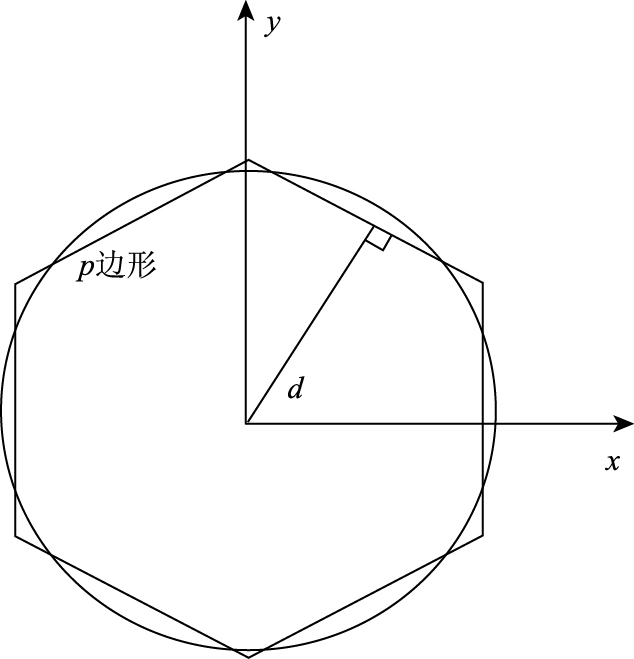
在此,我们来求等面积多边形逼近形式的每条边的方程,如图 2所示,为等面积正p边形。
|
| 图 2 等面积正p边形 Fig. 2 Homalographic regular polygon with p sides |
| |
很容易证明,当正p边形面积和半径为R的圆面积相等时,多边形的中心到任意一边的距离为:
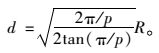
|
(5) |
因此,用d代替式(3) 中的R即可得到等面积正多边形逼近摩尔库伦屈服圆的每条边的方程:
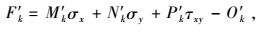
|
(6) |
式中,
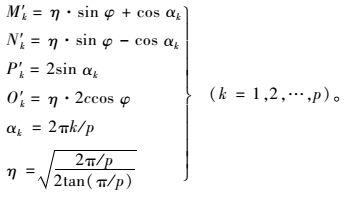
|
(7) |
极限分析上限法要求计算区域内的速度场满足速度相容条件及塑性相关联流动法则,对于平面应变条件下的理想刚塑性体,相关联流动法则表示为:
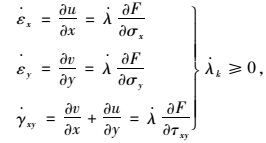
|
(8) |
式中,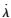
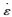
将线性化的摩尔库伦屈服函数式(6) 代入式(8),即可得到满足相关联流动法则的线性化塑性应变率表达式:
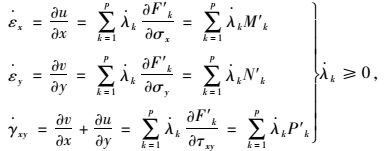
|
(9) |
式中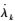
文中对于计算区域采用四边形单元[15]离散,四边形单元与三角形单元的最大不同就是形函数是非线性的,无法直接运用线性规划进行求解,对于此问题,我们只需通过对单元建立积分意义上的协调方程的弱形式即可,具体过程见文献[17]。
四边形单元内速度离散模式为:
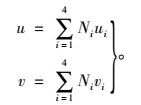
|
(10) |
将式(10) 代入式(9),并写成矩阵的表达形式,可以得到每个四边形单元内部的塑性流动约束条件:
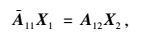
|
(11) |
式中,

|
(12) |
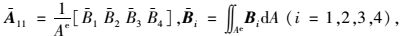
|
(13) |
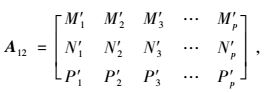
|
(14) |
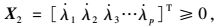
|
(15) |
式中Bi和Ae分别为应变矩阵和单元面积。
3 其他约束方程 3.1 速度间断线上塑性流动约束方程对摩尔库伦准则,当速度间断线上的塑性流动满足相关联流动法则时,则存在以下关系式:
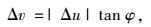
|
(16) |
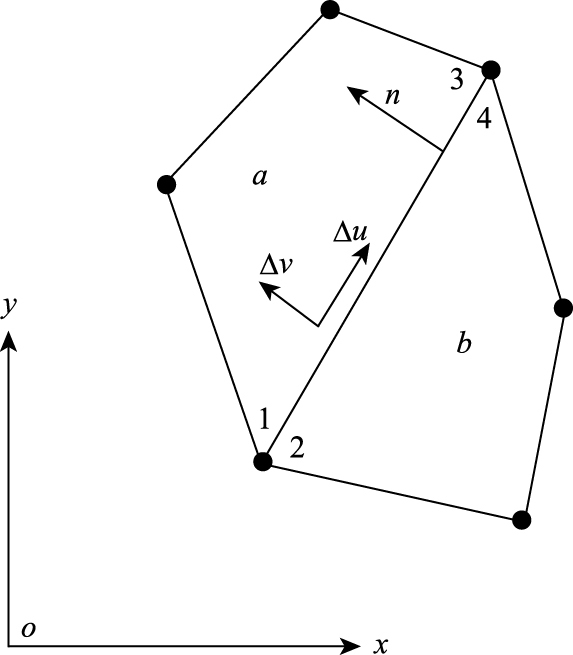
式中,Δv和Δu分别为速度间断线上任一点的法向和切向的相对速度,即相应的速度间断值,见图 3。
|
| 图 3 四边形单元速度间断线 Fig. 3 Velocity discontinuity line on quadrilateral element |
| |
按照文献[11]中的方法,对每对速度间断点引入一对非负变量u+和u-,令:
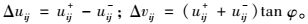
|
(17) |
因此,对于每条速度间断线,需要施加的塑性流动方程为:
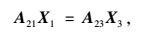
|
(18) |
式中,

|
(19) |
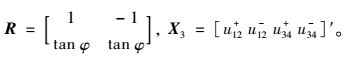
|
(20) |
设n为一速度边界的法向量,nx和ny为其分量,已知该边界上的切向和法向速度分别为u和v,则该边界上的节点i的速度分量需满足:
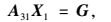
|
(21) |
式中,
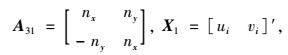
|
(22) |
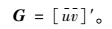
|
(23) |
(1) 单元内耗散功率
对于每个四边形单元,其内部相应的耗散能为:
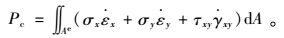
|
(24) |
将式(9) 代入并写成矩阵形式为:
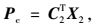
|
(25) |
式中,
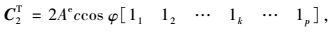
|
(26) |
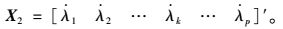
|
(27) |
(2) 间断线上功能耗散
在每条速度间断线上,由塑性剪切所产生的耗散能为:
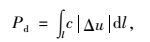
|
(28) |
式中l为间断线长度,令|Δu|=u++u-,代入式(28) 并写成矩阵形式可得:
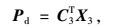
|
(29) |
式中,

|
(30) |
(3) 外部功率
外部功率是指节点荷载(外荷载等效移植)在节点速度上做的功,写成矩阵形式为:
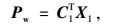
|
(31) |
式中,X1=[u1 v1 … um vm]′为节点速度向量; C1T= [px1 py1 … pxm pym]为节点荷载向量,m为节点总数。
4 线性规划模型在得到了所有约束条件后,通过虚功方程即可形成最后的优化函数,优化变量为单元节点速度分量、速度间断线辅助变量以及单元塑性乘子。
参考文献[18],我们可以通过对强度参数进行调整,来使超载系数逼近于1,从而得到不易直接求解的强度折减系数。由于我们求解的只是破坏时结构的破坏形式,它仅与X1的相对大小有关,因此令:

|
(32) |
此时,上限有限元法的数学模型为:
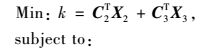
|
(32) |
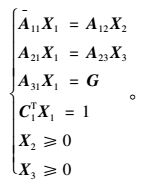
|
(33) |
文中算例是借助于matlab自编程序求解的。本算例取自文献[18],为一均质黏土边坡,坡比1:2,坡高10 m,材料的重度γ=20 kN/m3,内摩擦角φ=20°,黏聚力c= 10 kPa。边坡只受重力作用,边界条件为底部双向约束,两侧法向约束。网格划分如图 4所示。

|
| 图 4 边坡网格划分 Fig. 4 Meshing of slope |
| |
对本算例,当多边形边数采用6,8,12,15和25时,分别用外切多边形和等面积多边形逼近摩尔库伦屈服圆计算得到的安全系数见表 1和图 5。
| 边数p | 6 | 8 | 12 | 15 | 25 |
| Fs(外切逼近) | 1.583 | 1.512 | 1.432 | 1.410 | 1.406 |
| Fs(等面积逼近) | 1.435 | 1.418 | 1.412 | 1.406 | 1.405 |

|
| 图 5 安全系数与多边形边数p的关系 Fig. 5 Relation between safety factor and sides p of regular polygon |
| |
从图 5可以看到,采用等面积正多边形逼近摩尔库伦屈服圆很好地继承了上限有限元安全系数从上方逼近的性质,且收敛速度更快,在p=8时,即可达到很好的收敛精度,而对于外切多边形逼近形式达到相似的收敛度需要p=15左右,这大大地影响了计算效率。对本算例,用有限元强度折减法[18]和极限平衡法[19]得到的结果分别是1.40和1.380,这与文中方法在p=25时的安全系数1.405相近,说明了方法的可靠性。图 6为p=15时,边坡极限状态的速度场,从图中可明显看出滑动模式,可以为边坡支护提供帮助。

|
| 图 6 边坡极限状态速度场 Fig. 6 Velocity fields of slope in limit state |
| |
6 结论
文中引入等面积多边形到边坡上限分析法。针对传统的外切多边形逼近摩尔库伦屈服圆计算效率过慢、待优化变量过多的缺点,放松边坡内任一点均需严格满足上限性质的要求,提出了基于等面积多边形逼近形式的上限有限元法,推导出了相应的流动约束方程。
该方法很好地继承了上限法从上方收敛的性质,且具有更快的收敛速度,在多边形边数较少时就能达到很好的收敛效果,求解规模较少,可大规模提高计算效率,建议在工程应用中推广。
| [1] | BISHOP A W. The Use of the Slip Circle in the Stability Analysis of Slopes[J]. Geotechnique, 1955, 5(1): 7-17 |
| [2] | SPENCER E. A Method of Analysis of the Stability of Embankments Assuming Parallel Inter-slice Forces[J]. Geotechnique, 1967, 17(1): 11-26 |
| [3] | SARMA S K. Stability Analysis of Embankments and Slopes[J]. Journal of the Geotechnical Engineering Division, 1979, 105(12): 1511-1524 |
| [4] | 孙聪, 李春光, 郑宏, 等. 基于软化本构的有限元强度折减法[J]. 岩石力学与工程学报, 2014, 33(10): 2147-2153 SUN Cong, LI Chun-guang, ZHENG Hong, et al. Finite Element Method of Strength Reduction with Softening Constitutive Model[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(10): 2147-2153 |
| [5] | 周翠英, 刘祚秋, 董立国, 等. 边坡变形破坏过程的大变形有限元分析[J]. 岩土力学, 2003, 24(4): 644-647, 652 ZHOU Cui-ying, LIU Zuo-qiu, DONG Li-guo, et al. Large Deformation FEM Analysis of Slopes Failure[J]. Rock and Soil Mechanics, 2003, 24(4): 644-647, 652 |
| [6] | DRUCKER D C, GREENBERG H J, PRAGER W. The Safety Factor of an Elastic-Plastic Body in Plane Strain[J]. Journal of Applied Mechanics, 1951, 18: 371-378 |
| [7] | DRUCKER D C, PRAGER W, GREENBERG H J. Extended Limit Design Theorems for Continuous Media[J]. Quarterly of Applied Mathematics, 1952, 9(4): 381-391 |
| [8] | CHEN W F, LIU X L. Limit Analysis in Soil Mechanics[M]. Amsterdam: Elsevier Science, 1990. |
| [9] | 陈祖煜. 土力学经典问题的极限分析上、下限解[J]. 岩土工程学报, 2002, 24(1): 1-11 CHEN Zu-yu. Limit Analysis for the Classic Problems of Soil Mechanics[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(1): 1-11 |
| [10] | LYAMIN A V, SLOAN S W. Upper Bound Limit Analysis Using Finite Element and Linear Programming[J]. International Journal for Numerical Analytical Methods in Geomechanics, 2002, 26(2): 61-77 |
| [11] | SLOAN S W, KLEEMAN P W. Upper Bound Limit Analysis Using Discontinuous Velocity Fields[J]. Computer Methods in Applied Mechanics and Engineering, 1995, 127(1): 293-314 |
| [12] | 王均星, 王汉辉, 张优秀, 等. 非均质土坡的有限元塑性极限分析[J]. 岩土力学, 2004, 25(3): 415-421 WANG Jun-xing, WANG Han-hui, ZHANG You-xiu, et al. Plastic Limit Analysis of Heterogeneous Soil Slope Using Finite Elements[J]. Rock and Soil Mechanics, 2004, 25(3): 415-421 |
| [13] | 殷建华, 陈健, 李焯芬. 岩土边坡稳定性的刚体有限元上限分析法[J]. 岩石力学与工程学报, 2004, 23(6): 898-905 YIN Jian-hua, CHEN Jian, LEE C F. Upper Limit Analysis of Stability of Rock and Soil Slopes Using Rigid Finite Elements[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(6): 898-905 |
| [14] | 杨峰, 阳军生, 张学民. 基于线性规划模型的极限分析上限有限元的实现[J]. 岩土力学, 2011, 32(3): 914-921 YANG Feng, YANG Jun-sheng, ZHANG Xue-min. Implementation of Finite Element upper Bound Solution of Limit Analysis Based on Linear Programming Model[J]. Rock and Soil Mechanics, 2011, 32(3): 914-921 |
| [15] | 杨峰, 颜宾宾, 张箭, 等. 基于刚体平动运动单元上限有限元的毛洞隧道稳定性分析[J]. 公路交通科技, 2015, 32(12): 108-113 YANG Feng, YAN Bin-bin, ZHANG Jian, et al. Analysis of Unlined Tunnel Stability Based on FE Upper Bound of Rigid Translatory Moving Element[J]. Journal of Highway and Transportation Research and Development, 2015, 32(12): 108-113 |
| [16] | 高连生, 赵炼恒, 李亮, 等. 带台阶的多级边坡稳定性上限分析[J]. 公路交通科技, 2014, 31(6): 1-10 GAO Lian-sheng, ZHAO Lian-heng, LI Liang, et al. Analysis on Upper Bound of Stability of Multi-stage Slope with Benches[J]. Journal of Highway and Transportation Research and Development, 2014, 31(6): 1-10 |
| [17] | 孙聪, 李春光, 郑宏, 等. 基于四边形网格的边坡上限有限元法[J]. 岩石力学与工程学报, 2015, 34(1): 114-120 SUN Cong, LI Chun-guang, ZHENG Hong, et al. Upper Bound Limit Analysis of Slopes Using Quadrilateral Finite Elements[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 114-120 |
| [18] | 李国英, 沈珠江. 下限原理有限单元法及其在土工问题中的应用[J]. 岩土工程学报, 1997, 19(5): 84-89 LI Guo-ying, SHEN Zhu-jiang. Lower Bound Finite Element Method and Its Application in Geotechnical Problems[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(5): 84-89 |
| [19] | GRIFFITHS D V. Slope Stability Analysis by Finite Elements[J]. Géotechnique, 1999, 49(3): 387-403 |
 2017, Vol. 34
2017, Vol. 34
