扩展功能
文章信息
- 许海亮, 何炼, 何兆才, 安栋
- XU Hai-liang, HE Lian, HE Zhao-cai, AN Dong
- 考虑路面不平整度因素的车路耦合系统非线性数值模型
- A Nonlinear Numerical Model of Vehicle-pavement Coupled System Considering Pavement Roughness
- 公路交通科技, 2017, 34(8): 23-28
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(8): 23-28
- 10.3969/j.issn.1002-0268.2017.08.004
-
文章历史
- 收稿日期: 2017-04-06
车辆与道路的相互作用问题,包括车辆和道路两个系统的研究。车辆在路面不平整度的激励下产生振动,这种振动反过来又作用于道路结构,引起道路结构的变形,进而又加剧了车辆的振动,因此必须把车路作为一个大的系统进行研究[1-5]。对于车路耦合随机振动方面的研究主要采用如下几种方式:(1) 利用车辆模型,研究路面随机不平整度激励下车辆的振动,并计算出车辆对路面结构的动力荷载,再以该荷载来研究路面结构的响应[6-7];(2) 直接假定某种波动荷载为模拟的车辆荷载进行道路结构的动力响应研究[8-9];(3) 建立车路耦合线弹性模型,利用随机振动相关理论采用频域分析方法对问题进行研究[10-11]。
方法(1)、(2) 都将车辆和道路系统分离进行研究,没有完全反映出车路耦合振动的实际状况;方法(3) 一般利用线弹性模型,在频域内对问题进行研究,通过建立激励和响应间的对应关系,得到响应的频谱,从而可以考察系统振动的频率分布及变化规律,通过响应的频谱密度还可以得到描述响应的概率特征值,从概率角度得到问题的描述。但是方法(3) 还存在不足:利用线性模型得到的频域分析结果都是中心化的,也就是说得到的结果是由单纯的随机振动引起,不包含车辆在平衡位置时的变形,因此对于振动响应的描述并不全面;虽然通过对频率响应的逆变化可以得到振动的时域表达,但是得不出道路某一断面的振动特性。
针对上述方法研究中的不足,为了更为全面地研究车路耦合随机振动问题,文中利用Ansys有限元数值模拟方法,建立车路耦合系统的非线性数值模型,在时域范畴内,对问题进行研究。
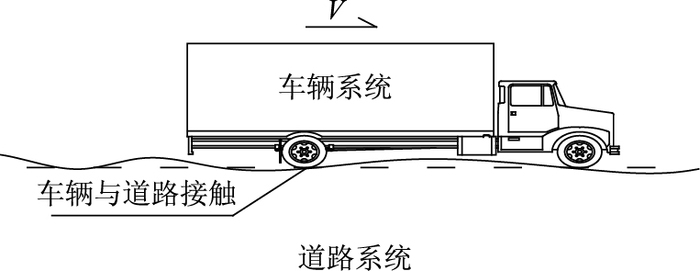
1 车路耦合系统非线性数值模型的建立车路耦合系统非线性模型的建立包括3大部分:车辆系统、道路系统以及车辆与道路的接触,如图 1所示。
|
| 图 1 车路耦合系统非线性模型 Fig. 1 Nonlinear model of vehicle-pavement coupled system |
| |
对于车路耦合模型的每一部分来说,都包含大量的非线性因素,如车辆中的摩擦减震器,道路系统中的黏塑性变形以及轮胎和路面的接触等。为了避免考虑太多非线性因素而给问题的数值求解收敛带来困难,文中模型中只考虑了车辆与道路的接触非线性问题,建立了系统的二维数值模型。
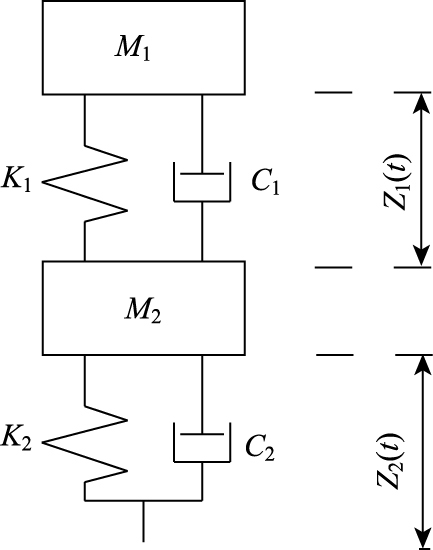
1.1 车辆系统数值模型文中研究问题的重点在于车辆-道路耦合系统中道路的结构响应问题,为突出主要问题,避免问题过于复杂而使求解变得困难,在非线性振动模型中车辆仍采用1/4车辆模型,据相关的国内外研究资料表明[7, 12],该车辆模型在相关的研究中应用较为广泛,能满足计算精度需求。车辆模型如图 2所示。
|
| 图 2 四分之一车辆模型 Fig. 2 Quarter vehicle model |
| |
图中, M1为悬挂系统(车架、载重)的质量;M2为非悬挂系统(轮胎、轮轴)的质量;K1为悬挂系统刚度;K2为非悬挂系统刚度;C1为悬挂系统阻尼;C2为非悬挂系统阻尼;Z1为悬挂系统与非悬挂系统的相对位移;Z2为非悬挂系统与路面的相对位移。
根据图 2所示,采用质量单元MASS21和弹簧阻尼单元COMBIN14来模拟车辆力学模型:采用两个质量单元来分别模拟车辆的悬挂系统质量和非悬挂系统质量;采用两个弹簧阻尼单元来模拟两个系统间及车辆与道路间的弹簧、阻尼。
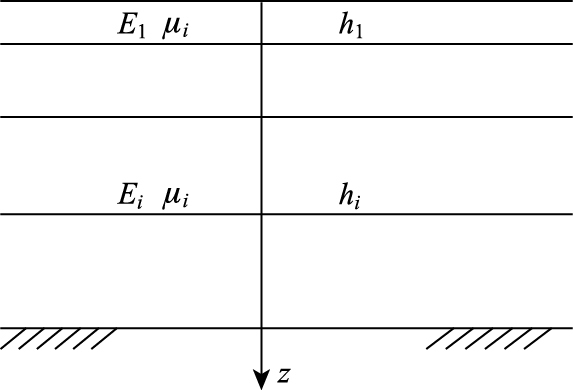
1.2 道路系统数值模型目前沥青混凝土路面应用较为广泛,因此文中所研究的道路结构模型针对沥青混凝土路面结构进行建立。沥青混凝土路面通常是由多层材料组成,如图 3所示。
|
| 图 3 道路结构力学模型 Fig. 3 Mechanical model of pavement structure |
| |
图 3中,根据道路结构设计组成,路面分上面层、中面层、下面层3个层次建模,路基分为基层、垫层和土路基3个层次建模。层间作用考虑为连续无滑动。道路结构取用二维实体结构单元PLANE42和PLANE2进行。图中E为弹性模量;μ为泊松比;h为厚度。
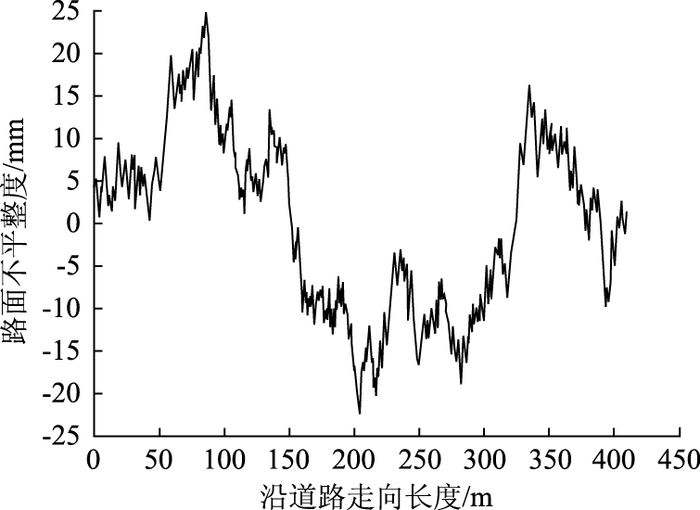
1.3 路面不平整度的时域仿真对于频域分析方法,路面不平整度的功率谱可以直接输入到系统的振动方程,对响应进行求解。而对于时域内的非线性模型,由于需要在时域内进行计算,路面不平整度需要被表达成空间形式。文中利用道路不平整度频谱进行Fourier逆变换得到时域模拟的路面不平整度数值,该方法主要思想是:根据路面不平整度功率谱分别求出频谱的幅值和随机相位,然后再通过傅立叶逆变换(IFFT)得到路面不平顺的时域模拟样本[13-14]。图 4为利用该方法得到的A级路面不平整度时域仿真结果示意图。同理可得到B级、C级等不同级别的路面不平整度仿真数值。
|
| 图 4 A级路面的不平整度时域曲线 Fig. 4 Roughness time-domain curve of Level A pavement |
| |
1.4 路面不平整度仿真数值的输入
如果采用ANSYS软件提供的通用前处理模块按照不平整度的空间形式建模,其工作量是巨大的,对问题的分析研究完成起来是很困难。面对这一困难,文中利用ANSYS软件提供的二次开发平台,利用APDL参数化设计语言编写了相应程序,根据得到的路面不平整度时域仿真数据可快捷地完成对路面不平整度空间形式的建模,大大提高了分析效率。
1.5 车路耦合关系数值模型的建立文中在建立车路耦合关系模型中采用了动点激振模型,将车辆作用力分布在长度为0.2 m的线荷载上,选用单元CONTA48进行描述车辆与路面的接触和跳起。同时利用一个密度为0,刚度无限大的平面模型将车辆的点荷载转换为线荷载,以更好地模拟轮胎与路面间的垂向作用力。为保持车辆匀速行驶,模型中没有考虑轮胎与路面间摩擦力的影响。
1.6 车路耦合模型边界条件及单元划分道路模型尺寸的确定必须考虑以下因素:在长度方向上能够满足车辆模型按某一速度运行一段时间,在深度方向上必须大于车辆荷载的影响范围,并且模型的计算规模不要过大,综合考虑上述各种因素,确定道路模型的尺寸分别为:长度方向40 m,深度方向3 m。长度方向40 m可以基本保证按车辆常用速度有1 s以上的运行时间,现有的研究资料表明,深度方向取3 m也可以保证大于车辆动荷载在道路内的作用范围。道路模型的边界条件都定为固定约束,建立车路耦合非线性二维模型如图 5所示。

|
| 图 5 车路耦合非线性数值模型 Fig. 5 Nonlinear numerical model of vehicle-pavement coupled system |
| |
对模型进行单元划分后,共生成9 458个单元,12 967个节点。模型计算过程中,车辆模型在道路表面以某一设定速度匀速运动。
计算过程中为消除车辆和道路结构在计算初始由于本身重力作用产生的变形和振动影响,计算设置了3 s时长的振动稳定期,经对各种工况试算,3 s时长完全满足各种工况的振动稳定要求。
2 车路耦合系统非线性模型的验证文中建立的车路耦合非线性模型能够反映路面不平整度这一随机变量对车路耦合振动的影响。考虑到路面不平整度的随机性,模型的计算结果很难与现场实测数据进行具体的对比验证,鉴于此,对于车路耦合非线性模型的验证采用如下两种方式进行:(1) 通过与有限元静力数值计算结果对比,以验证动力模型计算结果数值的可靠性;(2) 通过与现场实测振动波形的总体振动趋势对比,以验证动力模型反映振动趋势的正确性。
2.1 与有限元静力数值模型计算结果对比道路结构的有限元静力数值计算目前应用很广泛,计算结果普遍被人们所接受,计算正确性也得到了人们的认可[15-16]。文中采用A级路面不平整度条件下车辆低速行驶的动力数值计算结果和相同荷载、相同道路参数下的静力数值计算结果进行对比。动力计算中选择A级路面和车辆低速行驶,目的是尽可能减少不平整度对振动系统的影响,使动力计算结果与静力具有一定的可比性。
动力与静力计算中,路面结构设计组成和材料参数如表 1所示(参数的选取参考了相关文献确定)。
| 结构层名称 | 厚度/cm | 弹性模量/
MPa | 泊松比 | 密度/
(kN·m-3) | |
| 面层 | 上面层 | 4 | 1 200 | 0.25 | 2.0 |
| 中面层 | 5 | 1 150 | 0.25 | 2.0 | |
| 下面层 | 7 | 1 100 | 0.25 | 2.0 | |
| 基层 | 40 | 900 | 0.3 | 1.9 | |
| 垫层 | 20 | 600 | 0.35 | 1.9 | |
| 路基 | 224 | 25 | 0.42 | 1.9 | |
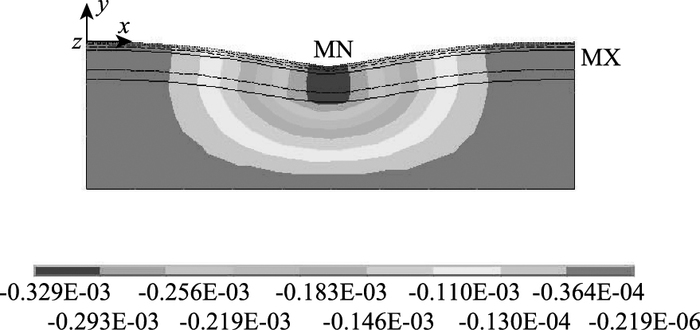
静力计算中车辆荷载取14 715 N。计算结果位移云图如图 6所示。
|
| 图 6 静力计算位移云图(单位:m) Fig. 6 Displacement nephogram under static loading(unit:m) |
| |
通过静力有限元计算,路面最大位移为0.329 mm。在动力计算中M1取1 350 kg,M2取150 kg,K1取1.5×105 N/m,K2取4.5×105 N/m,C1取4.5×103(N·s)/m,C2取1.5×103(N·s)/m,v取10 m/s(36 km/h),重力加速度取9.81。
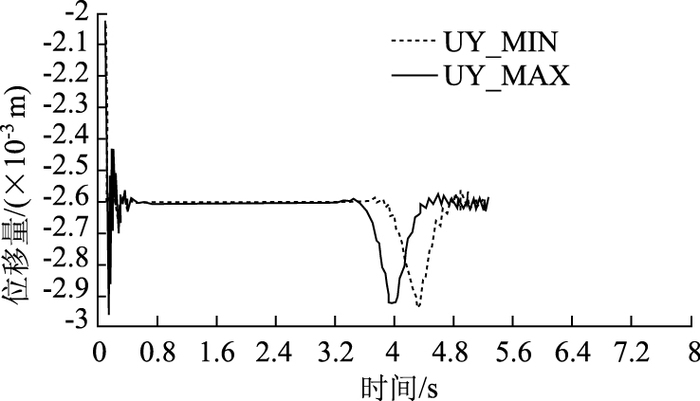
考虑随机动荷载作用下的路面位移是一变量,为能与静力结果准确进行对比,图 7绘出了计算过程中变形最大和最小节点的位移-时程曲线。
|
| 图 7 路面变形最大和最小节点的位移-时程曲线 Fig. 7 Displacement-time curves of maximum and minimum nodes of pavement deformation |
| |
整理数据后,可以得到,动力计算中路面最大位移变量是0.333 mm,最小位移变量是0.327 mm,两者与静力计算结果0.329 mm都比较接近,说明动力计算结果正确。
2.2 与已有的现场试验结果进行变化趋势对比文献[17]和文献[18]均对车辆行驶过程中路面的动力响应作了现场测试,以文献[17]中提到的现场测试为例。
文献[17]中,路面动位移响应试验采用891-Ⅱ型拾振器(中国地震局工程力学研究所)固定在待测路面附近,用于测量车辆通过时路面产生的动位移响应。
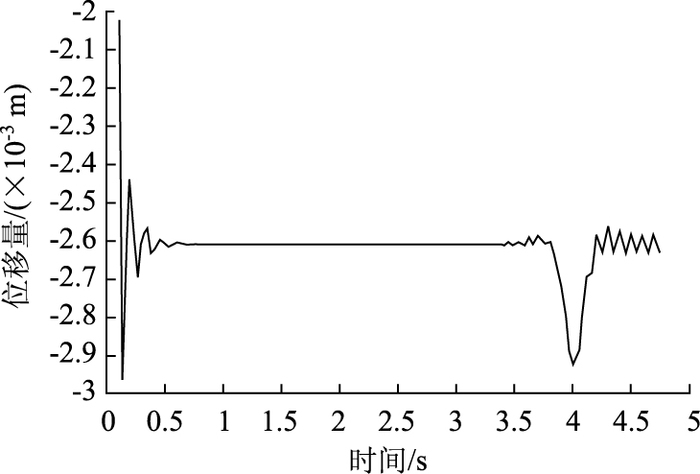
图 8为利用非线性模型,在A级路面v=60 km/h车速条件下计算得到的路面位移响应时程曲线。
|
| 图 8 v=60 km/h时路面动位移响应时程曲线 Fig. 8 Displacement-time curve of pavement dynamic displacement response when v=60 km/h |
| |
可以看出非线性模型计算所得时程曲线与实测曲线总体趋势一致,整个过程均大致分为3个阶段,暂称为:车辆临近、车辆进行和车辆离去。对于路面某一定点处的位移响应来说,车辆行驶临近时就已经产生位移振动,车辆驶离后,路面仍会保持一段时间的位移振动,这是静力模型计算所反映不出来的。虽然总体趋势一致,但实测波形与计算模拟波形还是存在一些差别,分析原因:(1) 受试验测量条件限制,现场试验采集点距车辆行驶点存在一定距离,并非车辆行驶点振动波形。(2) 车辆实际行驶中,车辆轮胎具有一定的滤波效应,这一点数值模型与实际情况有较大差别。通过对比,虽然存在一定的差别,但可以发现非线性模型与实测资料总体趋势能较好地符合,这验证了非线性模型建立的正确性。
3 车路耦合非线性数值模型算例应用考虑到我国运营道路的路面不平整度绝大部分分布在A, B, C三级,因此在路面不平整度对道路结构振动的影响研究中,路面不平整度时域模型只采用A, B, C三级,模型其他各参数取值同前。
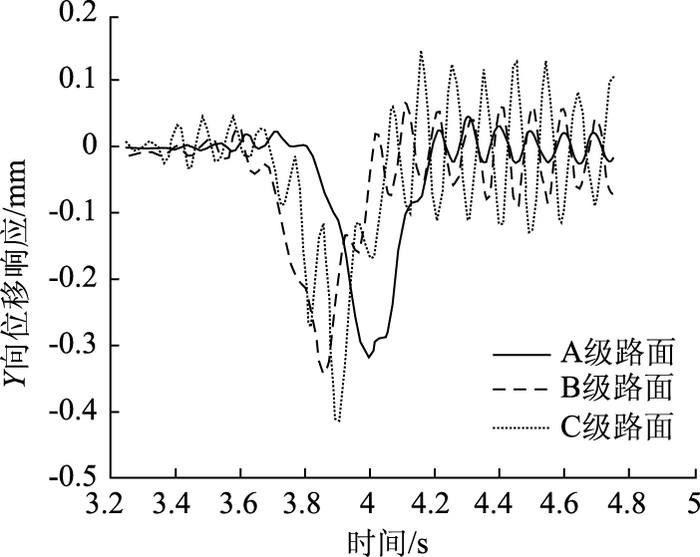
由图 9可以看出,路面平整度越差产生的振动位移也越大,C级路面下的最大位移量是A级路面的1.31倍,而在车辆离去阶段C级路面下的位移量是A级路面下的2~3倍。但路面高频部分振动频率受不平整度的影响不大。
|
| 图 9 不同路面不平整度条件下路面位移时程响应对比图(v=70 km/h) Fig. 9 Comparison of pavement displacement time history responses under different pavement roughnesses (v=70 km/h) |
| |
4 结论
(1) 建立了车路耦合非线性数值模型,经验证该模型能够很好地反映车路耦合系统的振动情况。
(2) 模型可以实现模拟车辆行驶和车轮的跳起,但没有考虑车路之间的摩擦力以及车辆轮胎的滤波效应,需要在今后的工作中进一步完善。
(3) 利用车路耦合非线性数值模型研究了不同路面不平整度情况下路面结构的振动情况,发现路面平整度越差产生的振动位移也越大,以算例为例C级路面下的最大位移量是A级路面的1.31倍,而在车辆离去阶段C级路面下的位移量是A级路面下的2~3倍,但路面高频部分振动频率受不平整度的影响不大。
| [1] | 何兆益, 刘炳森, 杜子学, 等. 重型车辆与路面耦合作用的仿真分析研究[J]. 公路交通科技, 2009, 26(3): 22-26 HE Zhao-yi, LIU Bing-sen, DU Zi-xue, et al. Analysis of Coupling Vibration Caused by Heavy-duty Vehicles and Road Pavement[J]. Journal of Highway and Transportation Research and Development, 2009, 26(3): 22-26 |
| [2] | 罗红, 梁波, 吴志华, 等. 半车车辆-道路耦合动力分析模型的研究与应用[J]. 应用数学和力学, 2014(7): 737-749 LUO Hong, LIANG Bo, WU Zhi-hua, et al. Study and Application of a 4-DOF 1/2 Vehicle-road Coupling Dynamic Model[J]. Applied Mathematics and Mechanics, 2014(7): 737-749 |
| [3] | 刘波, 王有志, 安俊江, 等. 车辆-路面空间耦合振动模型及其动力响应分析[J]. 山东大学学报:工学版, 2014(3): 83-89 LIU Bo, WANG You-zhi, AN Jun-jiang, et al. The Spatial Model of Vehicle-pavement Coupling Vibration and Its Dynamic Responses Analysis[J]. Journal of Shandong University:Engineering Science Edition, 2014(3): 83-89 |
| [4] | 仇敏玉, 俞亚南. 车辆荷载下地基数值模型的边界影响分析[J]. 公路交通科技, 2010, 27(1): 39-42, 49 QIU Min-yu, YU Ya-nan. Effect of Artificial Boundary on Numerical Model of Foundation under Vehicle Loads[J]. Journal of Highway and Transportation Research and Development, 2010, 27(1): 39-42, 49 |
| [5] | 倪富健, 王燕芳, 马翔. 城市道路交叉口沥青路面受力分析[J]. 公路交通科技, 2010, 27(7): 41-45 NI Fu-jian, WANG Yan-fang, MA Xiang. Mechanical Analysis of Asphalt Pavement in Urban Intersections[J]. Journal of Highway and Transportation Research and Development, 2010, 27(7): 41-45 |
| [6] | MIKHAIL M Y. Three Dimensional Mechanistic Analysis of Vehicle-pavement Interaction[D]. Phoenix:Arizona State University, 1996. http://environmental.cee.illinois.edu/node/72 |
| [7] | 孙璐, 邓学钧. 速度与车辆动态特性对于车路相互作用的影响[J]. 土木工程学报, 1997, 30(6): 34-40 SUN Lu, DENG Xue-jun. The Influences of Speed and Dynamic Characteristics of Truck on Vehicle-pavement Interactions[J]. China Civil Engineering Journal, 1997, 30(6): 34-40 |
| [8] | 张艳美. 高速公路路基的动力特性研究[D]. 兰州: 兰州铁道学院, 2001. ZHANG Yan-mei. Research on Dynamic Characteristics of Expressway Subgrade[D].Lanzhou:Lanzhou Railway Institute, 2001. http://cdmd.cnki.com.cn/Article/CDMD-10533-2010185865.htm |
| [9] | 陈华. 交通荷载作用下公路路基的动力有限元分析[D]. 兰州: 兰州理工大学, 2004. CHEN Hua. Dynamic Finite Element Analysis of Highway Subgrade under Traffic Load[D]. Lanzhou:Lanzhou University of Technology, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10731-2004102053.htm |
| [10] | 银花, 李懿. 车辆-沥青路面耦合系统相互作用研究[J]. 振动与冲击, 2013, 32(20): 107-112 YIN Hua, LI Yi. Interaction in a Vehicle Asphalt Pavement Coupled System[J]. Journal of Vibration and Shock, 2013, 32(20): 107-112 |
| [11] | 许海亮, 袁勇, 屈铁军, 等. 考虑路面不平整度因素的车路耦合振动模型的建立[J]. 振动与冲击, 2014, 33(19): 152-156 XU Hai-liang, YUAN Yong, QU Tie-jun, et al. Dynamic Model for a Vehicle-pavement Coupled System Considering Pavement Roughness[J]. Journal of Vibration and Shock, 2014, 33(19): 152-156 |
| [12] | 邓学均, 孙璐. 车辆-地面结构系统动力学[M]. 北京: 人民交通出版社, 1998. DENG Xue-jun, SUN Lu. Dynamics of Vehicle-pavement Structure System[M]. Beijing: China Communications Press, 1998. |
| [13] | 陈果. 车辆-轨道耦合系统随机振动分析[D]. 成都: 西南交通大学, 2000. CHEN Guo. Analysis of Random Vibration of Vehicle-track Coupling System[D].Chengdu:Southwest Jiaotong University, 2000. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013197985.htm |
| [14] | 王亚, 陈思忠, 郑凯锋. 时空相关路面不平度时域模型仿真研究[J]. 振动与冲击, 2013, 32(5): 70-74 WANG Ya, CHEN Si-zhong, ZHENG Kai-feng. Simulation Research on Time Domain Model of Road Roughness with Time-space Correlation[J]. Journal of Vibration and Shock, 2013, 32(5): 70-74 |
| [15] | 陆辉, 孙立军. 轮载作用下沥青路面三维非线性有限元分析[J]. 土木工程学报, 2004, 37(7): 64-67, 96 LU Hui, SUN Li-jun. Analysis on Asphalt Pavement under Tyre Load by Three-dimensional Finite Element Method[J]. China Civil Engineering Journal, 2004, 37(7): 64-67, 96 |
| [16] | 郝大力, 王秉纲. 路面结构动力响应分析[J]. 长安大学学报:自然科学版, 2002, 22(3): 9-12 HAO Da-li, WANG Bing-gang. Dynamic Response of Pavement Structure[J]. Journal of Chang'an University:Natural Science Edition, 2002, 22(3): 9-12 |
| [17] | 陈静. 车辆与路面相互作用的基础研究[D]. 长春: 吉林大学, 2002. CHEN Jing. Research on Vehicle-pavement Interaction Basis[D]. Changchun:Jilin University, 2002. http://cdmd.cnki.com.cn/Article/CDMD-10533-2008166156.htm |
| [18] | 朱孔源. 车辆-柔性路面力学相互作用系统的研究[D]. 北京: 中国农业大学, 2001. ZHU Kong-yuan. Study on Interaction between Vehicle and Flexible Pavement System[D].Beijing:China Agricultural University, 2001. http://cdmd.cnki.com.cn/Article/CDMD-10019-2001011673.htm |
 2017, Vol. 34
2017, Vol. 34
