扩展功能
文章信息
- 胡立伟, 李林育, 王淼, 佘天毅
- HU Li-wei, LI Lin-yu, WANG Miao, SHE Tian-yi
- 基于台架试验的长下坡路段满载中型货车制动风险阈值研究
- Study on Braking Risk Threshold Value for Full-loaded Medium Trucks on Continuous Long and Steep Downhill Sections Based on Bench Test
- 公路交通科技, 2017, 34(7): 135-144, 152
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(7): 135-144, 152
- 10.3969/j.issn.1002-0268.2017.07.019
-
文章历史
- 收稿日期: 2016-03-07
危急情况下汽车的制动器能否在极短时间内使车速迅速下降,并且在制动过程中保持方向的稳定性,已成为货运车辆在驾驶过程中危及道路交通安全的重要因素[1]。在山区长下坡路段,货车制动频繁,其制动器由于温度过高会产生“热衰退”现象而导致制动失灵[2]。因此,近年来很多汽车都利用辅助制动器作为补充制动措施,以防止行车制动器出现部分或完全失效。尽管如此,货车事故率依然居高不下[3]。对此,国外的学者很早就开始了在鼓式制动器的温升特性及制动性能方面的研究。J.Voldrich[4],A. Yevtushenko等[5]通过有限元分析软件对鼓式制动器进行了热力耦合分析,并进一步指出制动器热问题的根源在于温度场-应力场耦合效应。Z. Olesiak等[6]分析了制动过程中制动器的温度变化与磨损变化情况,最终得到制动器温升数学模型与磨损量数学模型。
目前国内学者徐银桥[7]、陈兴旺[8]、赵凯辉等[9]利用制动器台架试验对鼓式制动器开展了研究,但多集中在利用台架试验数据做辅助对比验证,进而确定整车道路试验或者软件仿真模型的准确性。王静[10]、纪王芳等[11]也通过台架试验从温升与能量的关系、制动器的结构设计、材料选型等方面开展了对制动器性能的研究。
综上所述,在制动器温度变化领域的研究中,国内外学者虽然通过大量的台架试验并结合辅助分析软件模拟研究了温升特性及制动效能,但在山区长下坡路段的制动风险阈值方面研究较少。本文正是基于中型货车鼓式制动器惯性台架试验,模拟中型载重货车长下坡路段持续制动工况下的热衰退试验。根据试验数据关系图,通过最小二乘逼近求出制动次数和温度的二维关系模型,进而预测出温度上升趋势,找出失效温度阈值及与之对应的最大临界制动次数,同时应用TableCurve2D软件对最小二乘拟合的方程进行模型的回归分析、参数检验、趋势预测,并基于试验数据在TableCurve2D下实现傅里叶多项式、切比雪夫多项式和有理方程的拟合建模与预测,通过拟合优度、标准误差、最大绝对误差、F值及P值的对比,筛选出拟合精度高且具有良好连续性、光滑性和保形性的曲线,最后通过改进的二项式系数法确定每个预测模型权系数,建立组合预测模型,获得制动风险阈值,并用留一交叉验证法确定预测模型的稳健性及预测结果的可靠性。
1 试验方案设计及数据收集 1.1 试验方案设计根据《商用车辆行车制动器技术要求及台架试验方法》(QC/T 239—2015)[12]以及相应的技术规程,构建汽车制动器试验台架,通过实验室台架试验对汽车制动系进行测试分析,研究制动器温度变化规律及其影响因素,探讨制动器温度与制动效能的关系,为汽车制动系温度报警决策算法提供依据。
试验样品:TD485后制动器总成3件。样品要求:全新完整的制动器产品,气压鼓式制动器需提供制动鼓、制动蹄、凸轮轴、凸轮轴支架、调整臂、制动气室等;制动衬片应保证同一批次。
试验台转动惯量的确定:车辆总质量加上旋转部分当量修正值,然后把相当于该质量的转动惯量按各轴制动力分配比分配,表达式为:
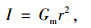
|
(1) |
式中,I为转动惯量计算值;Gm为将汽车满载总质量按制动力分配比设计值分配给被试制动器所对应车轮承受的那部分质量,当同一制动器用于不同车型时,取最大值;r为车轮滚动半径。
试验样品有关参数见表 1。
| 参数名称 | 数值 |
| 整车满载质量Ga/kg | 16 910 |
| 整车空载质量G0/kg | 11 920 |
| 最高车速Vmax/(km·h-1) | 90 |
| 车轮滚动半径r/mm | 540 |
| 前后轴制动力比β | 4:6 |
| 额定制动管路压力Pe/MPa | 0.8 |
| 满载试验转动惯量Ia/(kg·m2) | 1 596 |
| 超载试验转动惯量Ic/(kg·m2) | 3 500 |
按照试验要求的车速,预先计算出试验台安装制动鼓轴的相应转速值,具体计算式为:
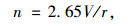
|
(2) |
式中,n为试验转速;V为试验车速;r为车轮滚动半径。
根据《商用车辆行车制动器技术要求及台架试验方法》[12]的要求,分别以40,50,60,70 km/h的初速度v0,控制制动管路压力使制动减速度为0.07g、首次拖磨制动初温≤60 ℃,每次拖磨12 s,频率为1次/min,各进行60次拖磨制动,试验过程中关闭风机。按以上方案重复做10次,获取10组试验样本,每次制动时记录制动管路压力、输出制动力矩、制动鼓温度、制动衬片温度、并确定各车速下制动力矩急剧变化时的温度、次数,即衰退率首次大于25%的临界点。
1.2 试验数据收集管路压力P、制动温度T等信号通过安装在管路和制动器上的传感器进行测量,制动力矩MB由固定安装在制动装置上的扭矩传感器收集,所有传感器信号由数据采集系统传入计算机分析系统。本试验将采用3种温度测量方法:(1) 将温度传感器安装在制动蹄片上,用制动蹄片的温度值来反映制动鼓的温度值;(2) 采用非接触式红外温度传感器对制动鼓外表面进行温度测量;(3) 将温度传感器埋入制动鼓中,进行直接测量。取3种测量方法的算术平均值作为测量结果。
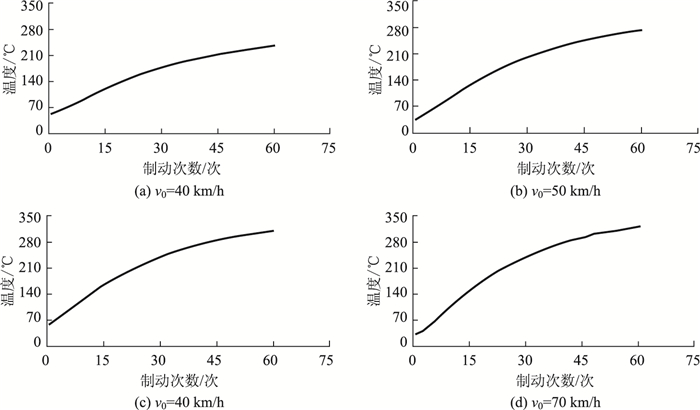
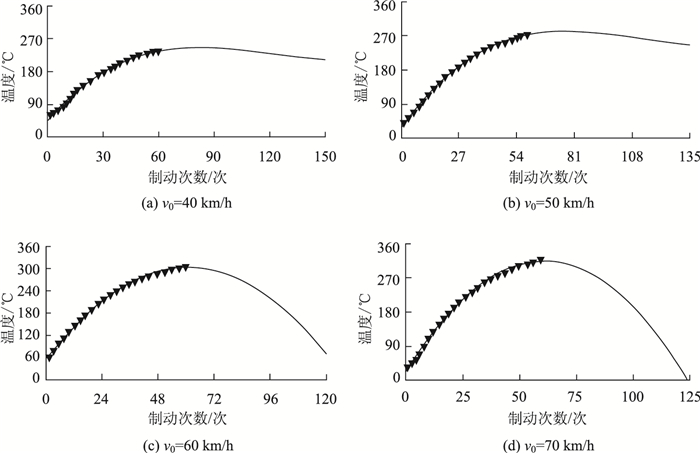
2 满载中型货车长下坡路段鼓式制动器温度变化特性分析 2.1 鼓式制动器温度变化规律根据模拟长下坡路段满载中型货车制动鼓热衰退试验的数据结果,绘制4组制动鼓温度变化值T与制动次数N之间的关系图(见图 1),为模型形式的选择提供必要的依据。由该图分析可知,T与N的趋势预测曲线可能存在多项式的关系(假设为多项式)。因此,初步决定的模型基本形式为:
|
| 图 1 不同制动初速度下温度与制动次数关系 Fig. 1 Relationship between temperature and braking number at different initial braking speeds |
| |
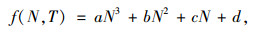
|
(3) |
式中,a,b,c,d为待定回归系数,T和N表示制动鼓温度与制动次数。
2.2 鼓式制动器温度变化拟合建模分析采用最小二乘逼近对试验数据进行曲线拟合,设函数T=S*(N)与试验数据得到的离散点集{(Ni, Ti), i=1, …, 60}拟合,若记误差δi=S*(Ni)-Ti(i=1, …, 60),δ=(δ1, δ2, …, δ60)T,设Φ0(N), Φ1(N), …, Φn(N)为C[1,N](N≤m)上的线性无关函数族,在函数族Φ=span{Φ0(N), Φ1(N), …, Φn(N)}中找一函数S*(N),使误差平方和最小,即:
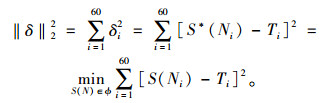
|
(4) |
设S*(N)=aN3+bN2+cN+d,将其代入式(4) 得:
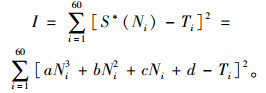
|
(5) |
分别在等式两边对待定参数a,b,c,d求偏导,并令其等于零,得:
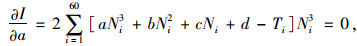
|
(6) |
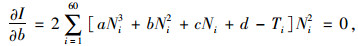
|
(7) |
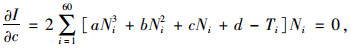
|
(8) |
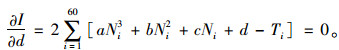
|
(9) |
将试验数据代入以上4个偏导公式中,即可求得拟合的多项式曲线。根据最小二乘逼近,拟合出温度T与制动次数N的关系(见表 2),在温度下降拐点得到制动鼓失效温度即危险温度阈值,同时得到与之对应的临界最大制动次数。
| 试验条件 | 拟合公式 (x:制动次数,y:温度/℃) |
参数值 | 临界最大 制动次数 |
危险温度阈 值/℃ |
| v0=40 km/h | y=a+bx+cx2+dx3① | a=45.551 2,b=5.873 5,c=-0.053 9,d=0.000 1 | 82 | 246.335 2 |
| v0=50 km/h | a=26.822 5,b=7.948 4,c=-0.078 1,d=0.000 2 | 78 | 281.392 7 | |
| v0=60 km/h | a=54.480 2,b=8.154 5,c=-0.066 9,d=0.000 0 | 61 | 302.910 2 | |
| v0=70 km/h | a=20.905 7,b=9.680 2,c=-0.079 5,d=0.000 0 | 61 | 315.503 2 |
应用TableCurve2D软件对最小二乘拟合的方程进行模型的回归分析、参数检验、趋势预测,并在TableCurve2D下进行傅里叶多项式、切比雪夫多项式及有理方程的拟合建模及分析。制动鼓温度的拟合曲线方程及模型分析概述见表 3~表 10。
| 试验条件 | 拟合公式(x:制动次数,y:温度/℃) | 危险温度 阈值/℃ |
临界最大制 动次数/次 |
| v0=40 km/h (满载) |
傅里叶多项式: y=a+bcos x+csin x+dcos(2x)+esin(2x)+fcos(3x)+gsin(3x),a=174.636 2, b=-91.051 7, c=-14.397 8, d=-26.473 4, e=20.632 4, f=0.956 8, g=7.089 6② | 266.455 0 | 77 |
| 切比雪夫多项式:y=a+bT1(t)+cT2(t)+dT3(t),a=161.202 6, b=91.320 6, c=-17.563 6, d=0.947 4,Tn(x)=cos(n·arccos x),-1≤x≤1③ | 246.335 2 | 82 | |
| 有理方程:y=(a+cx0.5)/(1+bx0.5+dx), a=33.476 0, b=-0.167 9, c=7.849 9, d=0.011 7④ | 239.198 0 | 73 |
| 方程序号 | 拟合优度 | 校正决定系数 | F值 | P值 | 标准误差 | 最大绝对误差 |
| ① | 0.998 866 | 0.998 784 | 16 442.333 5 | 0 | 1.897 7 | 7.029 0 |
| ② | 0.999 857 | 0.999 838 | 61 955.491 1 | 0 | 0.691 6 | 1.863 9 |
| ③ | 0.998 866 | 0.998 784 | 16 442.333 5 | 0 | 1.897 7 | 7.029 0 |
| ④ | 0.998 100 | 0.997 961 | 9 804.118 3 | 0 | 2.456 6 | 9.426 5 |
| 试验条件 | 拟合公式(x:制动次数,y:温度/℃) | 危险温度 阈值/℃ |
临界最大制 动次数/次 |
| v0=50 km/h (满载) |
傅里叶多项式: y=a+bcos x+csin x+dcos(2x)+esin(2x)+fcos(3x)+gsin(3x),a= 173.786 1, b=120.774 8, c=18.365 8, d=-16.768 6, e=31.100 7, f=3.720 7, g=5.182 2② | 282.668 8 | 69 |
| 切比雪夫多项式:y=a+bT1(x)+cT2(x)+dT3(x),a=178.381 8, b=117.429 7, c=-24.774 7, d=1.484 5,Tn(x)=cos(n·arccos x),-1≤x≤1③ | 281.392 7 | 78 | |
| 有理方程:y=(a+cx0.5+ex+gx1.5)/(1+bx0.5+dx+fx1.5+hx2),a=30.489 1, b=-0.467 2, c=-8.793 3, d=0.103 2, e=2.746 0, f=-0.010 1, g=-0.115 2, h=0.000 4④ |
281.328 1 | 74 |
| 方程序号 | 拟合优度 | 校正决定系数 | F值 | P值 | 标准误差 | 最大绝对误差 |
| ① | 0.999 573 | 0.999 542 | 43 705.984 7 | 0 | 1.517 0 | 2.738 4 |
| ② | 0.999 892 | 0.999 877 | 81 692.400 9 | 0 | 0.776 5 | 2.789 7 |
| ③ | 0.999 573 | 0.999 542 | 43 705.984 7 | 0 | 1.501 1 | 4.707 1 |
| ④ | 0.999 876 | 0.999 856 | 59 809.135 8 | 0 | 0.840 2 | 3.041 2 |
| 试验条件 | 拟合公式(x:制动次数,y:温度/℃) | 危险温度 阈值/℃ |
临界最大制 动次数/次 |
| v0=60 km/h (满载) |
傅里叶多项式: y=a+bcos x+csin x+dcos(2x)+esin(2x)+fcos(3x)+gsin(3x),a=189.565 0, b=-130.501 4, c=49.101 3, d=-5.378 0, e=39.555 2, f=6.907 8, g=3.213 0② | 310.876 2 | 66 |
| 切比雪夫多项式:y=a+bT1(x)+cT2(x)+dT3(x)+eT4(x)+fT5(x),a=211.912 9, b=121.560 4, c=-28.910 7, d=2.790 0, e=0.450 2, f=-0.391 7,Tn(x)=cos(n·arccos x),-1≤x≤1③ | 311.113 0 | 67 | |
| 有理方程:y=(a+cx0.5)/(1+bx0.5+dx),a=29.937 5, b=-0.160 6, c=16.142 4, d=0.012 5④ | 310.058 1 | 72 |
| 方程序号 | 拟合优度 | 校正决定系数 | F值 | P值 | 标准误差 | 最大绝对误差 |
| ① | 0.999 241 | 0.999 201 | 37 539.911 7 | 0 | 2.057 3 | 5.047 4 |
| ② | 0.999 967 | 0.999 963 | 269 327.308 8 | 0 | 0.443 6 | 2.618 6 |
| ③ | 0.999 932 | 0.999 925 | 159 812.603 8 | 0 | 0.630 9 | 2.798 4 |
| ④ | 0.999 560 | 0.999 528 | 42 401.254 1 | 0 | 1.580 8 | 7.309 0 |
| 试验条件 | 拟合公式(x:制动次数,y:温度/℃) | 危险温度 阈值/℃ |
临界最大 制动次数 |
| v0=70 km/h (满载) |
傅里叶多项式: y=a+bcos x+csin x+dcos(2x)+esin(2x)+fcos(3x)+gsin(3x), a=210.089 0, b=-146.475 9, c=10.396 5, d=-32.534 1, e=37.012 6, f=2.552 9, g=10.924 5② | 338.239 7 | 73 |
| 切比雪夫多项式: y=a+bT1(x)+cT2(x)+dT3(x)+eT4(x)+fT5(x)+ gT6(x)+hT7(x),a=208.022 4, b=143.444 9, c=-33.531 1, d=2.240 9, e=2.139 8, f=-2.338 9, g=1.489 3, h=-0.425 1,Tn(x)=cos(n·arccos x),-1≤x≤1③ | 325.811 6 | 66 | |
| 有理方程:y=(a+cx+ex2+gx3)/(1+bx+dx2+fx3+hx4), a=29.244 1, b=-0.009 8, c=6.422 4, d=0.001 1, e=0.176 9, f=-1.625 2e-05, g=-0.002 6, h=5.493 4e-08④ | 329.149 9 | 70 |
| 方程序号 | 拟合优度 | 校正决定系数 | F值 | P值 | 标准误差 | 最大绝对误差 |
| ① | 0.998 780 | 0.998 715 | 23 333.378 8 | 0 | 3.094 9 | 5.855 1 |
| ② | 0.999 877 | 0.999 861 | 71 875.129 4 | 0 | 1.018 6 | 2.568 1 |
| ③ | 0.999 909 | 0.999 895 | 81 957.484 6 | 0 | 0.883 2 | 2.631 4 |
| ④ | 0.999 591 | 0.999 526 | 18 136.128 1 | 0 | 1.877 2 | 5.436 7 |
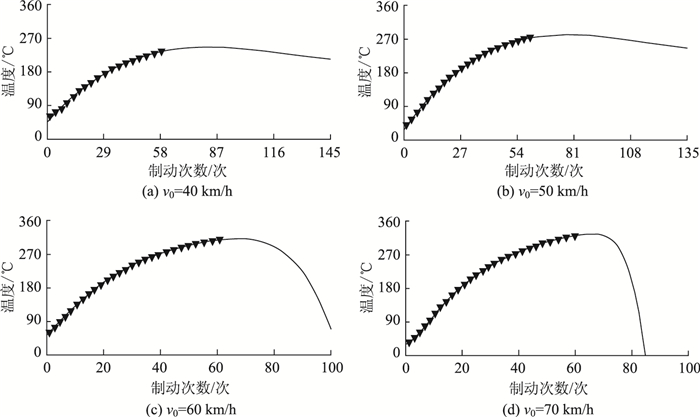
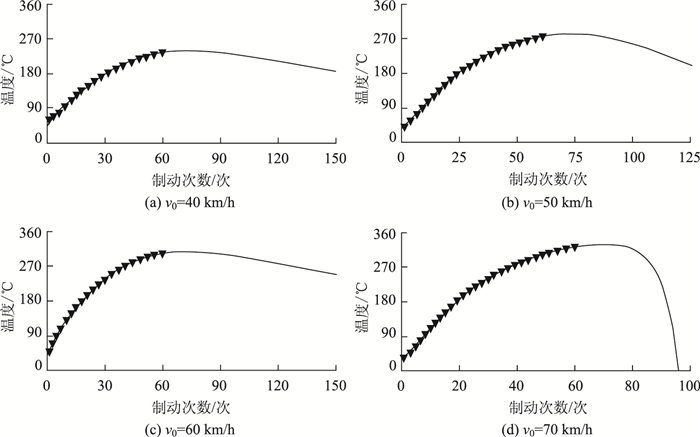
在TableCurve2D下,对最小二乘法模型、傅里叶多项式模型、切比雪夫多项式模型、有理方程模型进行未来趋势预测,其拟合曲线趋势预测结果(如图 2~图 5所示)。根据TableCurve2D软件对最小二乘拟合的方程进行模型的回归分析结果可以看出,4种不同初始速度下其拟合优度指数均约为0.99,说明假定的模型对数据有较好的解释能力,并且随着模型拟合优度的升高,其标准误差会减小,说明其对数据拟合得越好。从制动鼓温度曲线拟合的3种复杂多项式模型(傅里叶多项式、切比雪夫多项式、有理方程)中可以看出其P值≤0.05,可以被认为是具有统计学意义或者显著性差异,并且拒绝原假设(原假设认为制动鼓温度与制动次数没有关系,二者的均值相同等)。可以看出,4种拟合曲线不间断,说明其连续性较好。拟合曲线没有明显突变,图像光滑圆润,即具有较好的光滑性。
|
| 图 2 最小二乘法模型拟合曲线趋势预测 Fig. 2 Fitting curve trend prediction by Least square model |
| |
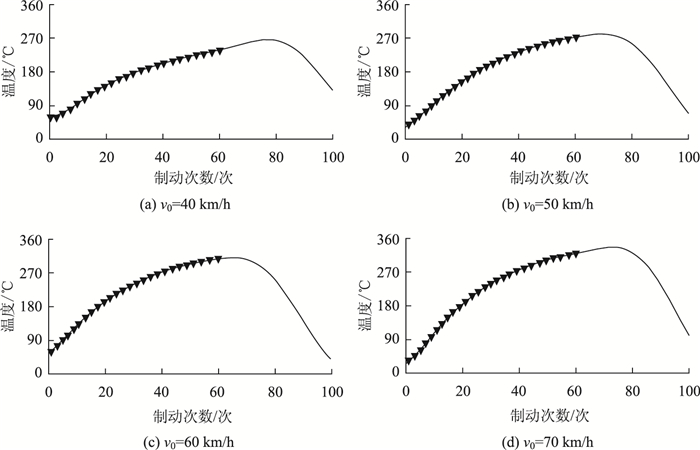
|
| 图 3 傅里叶多项式模型拟合曲线趋势预测 Fig. 3 Fitting curve trend prediction by Fourier polynomials model |
| |
|
| 图 4 切比雪夫多项式模型拟合曲线趋势预测 Fig. 4 Fitting curve trend prediction by Chebyshev polynomials model |
| |
|
| 图 5 有理方程模型拟合曲线趋势预测 Fig. 5 Fitting curve trend prediction by Rational equation model |
| |
为客观评价以上4个模型的拟合精度及对未来趋势的预测水平,文中拟采用平均绝对百分误差(MAPE)[13]作为评价精度指标,MAPE定义如下:
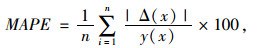
|
(10) |
式中, Δ(x)为预测残差;y(x)为试验观测值。MAPE精度评价分级见表 11[14]。通过试验观测值与各模型的预测结果,计算得到各模型的MAPE,结果见表 12。可以看出,不同初设条件下4种预测模型的MAPE均小于10,属于高精度拟合模型。
| MAPE | 拟合等级 | MAPE | 拟合等级 |
| <10 | 高精度拟合 | 20~50 | 可行的拟合 |
| 10~20 | 好的拟合 | >50 | 不可行的拟合 |
| 制动初速度/ (km·h-1) |
最小二乘法 模型 |
傅里叶多项 式模型 |
切比雪夫多 项式模型 |
有理方程 模型 |
| 40 | 1.26 | 0.36 | 1.27 | 1.64 |
| 50 | 1.01 | 0.35 | 1.03 | 0.37 |
| 60 | 0.99 | 0.15 | 0.27 | 0.80 |
| 70 | 1.83 | 0.53 | 0.37 | 1.19 |
| 制动初速度/ (km·h-1) |
最小二乘法 模型 |
傅里叶多项 式模型 |
切比雪夫多 项式模型 |
有理方程 模型 |
| 40 | 201.669 9 | 25.352 1 | 201.670 3 | 337.958 6 |
| 50 | 126.184 6 | 31.956 8 | 126.185 0 | 36.707 2 |
| 60 | 241.261 4 | 10.430 3 | 21.490 6 | 139.946 7 |
| 70 | 545.965 2 | 54.994 7 | 40.560 7 | 183.236 0 |
| 初设 条件 |
组合预测模型 | 危险温 度阈值/ ℃ |
临界最 大制动 次数/次 |
| v0= 40 km/h |
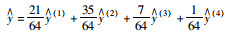 |
257.23 | 80 |
| v0= 50 km/h |
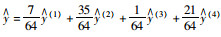 |
282.07 | 72 |
| v0= 60 km/h |
 |
310.74 | 69 |
| v0= 70 km/h |
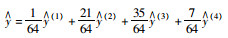 |
330.09 | 67 |
2.3 危险温度阈值及临界最大制动次数
为避免单一预测模型预测结果的片面性,综合考虑4个预测模型的4种不同预测结果,将4种预测模型以恰当的权重进行组合,提高预测精度及可靠性,建立组合预测模型:
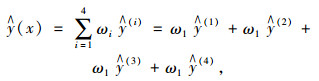
|
(11) |
式中,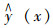
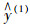
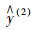
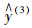
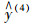
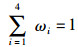
本文采用改进的二项式系数法确定单一预测模型的权系数[15-16]:
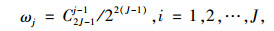
|
(12) |
式中,C2J-1i-1为二项式系数;i按照平方和误差(SSE)由大到小降序排列,因此权重与SSE为反序的关系,SSE按式(13) 计算,计算结果见表 13。
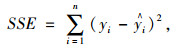
|
(13) |
式中,yi为试验值;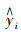
当v0=40 km/h时,按平方和误差降序排列,其模型顺序为:有理方程模型、切比雪夫多项式模型、最小二乘法模型、傅里叶多项式模型;当v0=50 km/h时,按平方和误差降序排列,其模型顺序为:切比雪夫多项式模型、最小二乘法模型、有理方程模型、傅里叶多项式模型;当v0=60 km/h时,按平方和误差降序排列,其模型顺序为:最小二乘法模型、有理方程模型、切比雪夫多项式模型、傅里叶多项式模型;当v0=70 km/h时,按平方和误差降序排列,其模型顺序为:最小二乘法模型、有理方程模型、傅里叶多项式模型、切比雪夫多项式模型。由此得到组合预测模型,并求得危险温度阈值及临界最大制动次数,结果见表 14。
2.4 模型验证交叉验证(Cross-validation)主要用于建模应用中模型的内部检验。在给定的建模样本中,选取大部分样本用于建模,剩下的小部分样本利用刚建立的模型进行预测,并求这小部分样本的预测误差,计算它们的平方和,通过有效重复地利用试验数据,充分显示了交叉验证法在模型选择和评估方面的优势[17]。通过交叉验证可得到高预测精确度和低预测误差的结果[18]。鉴于预测模型外部验证(山区长大下坡路段实车试验)的危险系数较高,文中采用留一交叉验证法通过内部效度对预测模型进行检验:将10组样本数据切割成2个互补的子集,其中抽取9组样本作为训练集,并取9组样本的均值用于建模,剩余的1组作为测试集用于验证预测模型的有效性。为了减少交叉验证结果的可变性,对10组样本数据集进行10次不同的划分,得到10组不同的互补子集,进行多次交叉验证,保证每个样本数据都被用于验证预测模型的有效性而且仅被预测验证了1次;通过计算出每个样本的验证误差的平方和(Predicted Error Sum of Squares,PRESS),筛选出PRESS最小的模型作为理想预测模型。
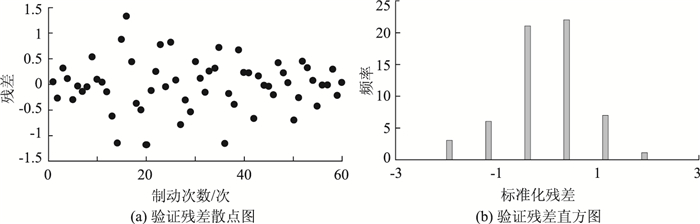
文中拟合建模所得的预测模型正是通过上述过程对10组样本数据进行筛选,最终确定了1个样本全集,其中9组样本的均值用作本次建模的基础试验数据,剩余1组作为测试集,检验组合预测模型的可行性和稳定性。组合预测模型的验证误差散点图及验证残差直方图如图 6~图 9所示。
|
| 图 6 验证残差散点图及验证残差直方图(v0=40 km/h) Fig. 6 Scattergram and histogram of validating residual error (v0=40 km/h) |
| |
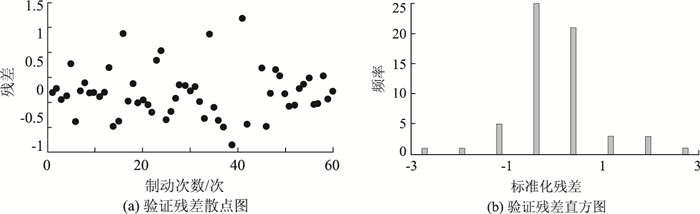
|
| 图 7 验证残差散点图及验证残差直方图(v0=50 km/h) Fig. 7 Scattergram and histogram of validating residual error (v0=50 km/h) |
| |
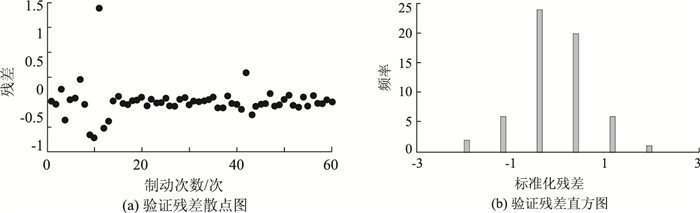
|
| 图 8 验证残差散点图及验证残差直方图(v0=60 km/h) Fig. 8 Scattergram and histogram of validating residual error (v0=60 km/h) |
| |
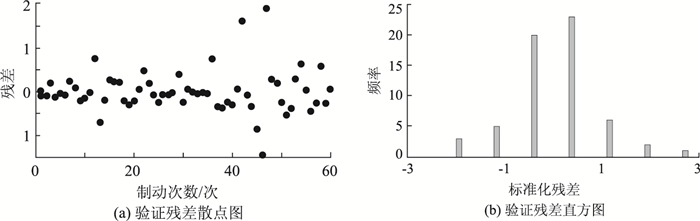
|
| 图 9 验证残差散点图及验证残差直方图(v0=70 km/h) Fig. 9 Scattergram and histogram of validating residual error (v0=70 km/h) |
| |
在残差散点图中,大多数的残差点较均匀地落在(-2, +2) 的水平带之间,且不带有任何系统趋势,完全随机地分布在该带状区域,说明对样本数据拟合良好,所建立的组合预测模型是稳定的。从标准化的验证残差直方图中可以看到4个直方图的形态基本符合正态分布,则可大体认为数据的残差是符合正态分布的,这表明组合预测模型是合理可行的。
3 结果分析初速度v0=40 km/h时,制动鼓的失效温度为257.23 ℃,其对应的最大临界拖磨制动次数为80次,即当中型货车在长下坡路段连续拖磨制动次数超过80次时,制动鼓会随着温度的迅速下降而开始失效;初速度v0=50 km/h时,制动鼓的失效温度为282.07 ℃,其对应的最大临界拖磨制动次数为72次,即当中型货车在长下坡路段连续拖磨制动次数超过72次时,制动鼓会随着温度的迅速下降而开始失效;初速度v0=60 km/h时,制动鼓的失效温度为310.74 ℃,其对应的最大临界拖磨制动次数为69次,即当中型货车在长下坡路段连续拖磨制动次数超过69次时,制动鼓会随着温度的迅速下降而开始失效;初速度v0=70 km/h的时,制动鼓的失效温度为330.09 ℃,其对应的最大临界拖磨制动次数为67次,即当中型货车在长下坡路段连续拖磨制动次数超过67次时,制动鼓会随着温度的迅速下降而开始失效。但在实际预测工作中,通过单存量的数学分析会忽视非量因素的影响而对预测结果造成偏差,所以实践工作中,必须定性与定量相结合,以定性为指导,定量计算为手段,才能更好地把握货车制动鼓的温升规律,并做出恰当的风险预测。
从各预测模型的图形趋势可以分析得出,用同一种预测模型进行预测,随着制动初速度的增大,其制动鼓温度就越易接近临界点,在其越过拐点后,曲线下降趋势越明显,这表明随着制动初速度增大,制动鼓越易达到失效状态,当其达到失效状态后,其失效的剧烈程度也会随着初速度的增大而加深,表现为制动鼓从开始部分失效到完全失效的过程会缩短。
4 结论制动鼓的“热衰退”现象是高原山地地区交通运输的重要安全隐患之一。文中通过实验室台架模拟试验,测试长下坡路段满载中型货车制动系统温度变化过程,分析不同制动初始速度下鼓式制动器温度变化规律并建立了组合预测模型,并得到如下结论:
(1) 在文中的试验条件下,制动初速度为40,50,60,70 km/h时,制动鼓发生“热衰退”的危险温度阈值分别为257.23,282.07,310.74,330.09 ℃,其对应的最大临界拖磨制动次数依次为80,72,69,67次。试验结果表明,随着初速度的不断增大,车辆的动能就会增大,在坡度大小相同的情况下转化为制动鼓的热能就越多,表现为制动器的失效温度值越高,但其最大临界制动次数却减小,说明制动初速度越大,越容易达到失效状态,当制动鼓发生“热衰退”现象后,其制动效能下降速率也会随着初速度的增大而增大,因此货车在长下坡路段应该保持低速行驶,以保障行车安全。
(2) 为避免单一预测模型的片面性,综合考虑每个预测模型的预测结果,通过改进的二项式系数法,科学地给各单一预测模型分配权重系数。由验证残差图可以看出,不同初速度下,组合预测模型的最大绝对误差小于2,均小于各相应的单一模型预测模型的最大绝对误差,从而减小了预测中的个别偶然误差,这表明科学的组合预测模型能更好地适应实际预测,提高预测的精度和可靠性。
| [1] | 雷正保, 乔维高, 姜华平. 交通安全概论[M]. 北京: 人民交通出版社, 2010. LEI Zheng-bao, QIAO Wei-gao, JIANG Hua-ping. Introduction to Traffic Safety[M]. Beijing: China Communications Press, 2010. |
| [2] | 靳恩勇, 杜博英. 长大下坡货车制动器温度模型[J]. 公路交通科技, 2011, 28(2): 133-136 JIN En-yong, DU Bo-ying. Prediction Model of Brake Temperature of Truck on Long and Steep Downgrade[J]. Journal of Highway and Transportation Research and Development, 2011, 28(2): 133-136 |
| [3] | 史培龙, 余强, 余曼, 等. 重型商用汽车长下坡制动器升温模型研究[J]. 公路交通科技, 2016, 33(1): 147-152 SHI Pei-long, YU Qiang, YU Man, et al. Research on Brake Heating Model for Heavy-duty Truck on Long Downhill[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 147-152 |
| [4] | VOLDRICH J. Frictionally Excited Thermo-elastic Instability in Disc Brakes:Transient Problem in the Full Contact Regime[J]. International Journal of Mechanical Sciences, 2007, 49(2): 129-137 |
| [5] | YEVTUSHENKO A, KUCIEJ M. Temperature and Thermal Stresses in a Pad/Disc during Braking[J]. Applied Thermal Engineering, 2010, 30(4): 354-359 |
| [6] | OLESIAK Z, PYRYEV Y. YEVTUSHENKO A. Determination of Temperature and Wear during Braking[J]. Wear, 1997, 210(1/2): 120-126 |
| [7] | 徐银桥. 轻型载货汽车持续制动性能研究[D]. 南京: 南京理工大学, 2016. XU Yin-qiao. Research on Continuous Braking Performance of Light Truck[D]. Nanjing:Nanjing University of Science and Technology, 2016. http://d.wanfangdata.com.cn/Thesis/Y683360 |
| [8] | 陈兴旺. 鼓式制动器制动温度场的研究[D]. 西安: 长安大学, 2006. CHEN Xing-wang. Research on Temperature Field of Brake Drum[D]. Xi'an:Chang'an University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-11941-2006163517.htm |
| [9] | 赵凯辉. 汽车制动器热衰退性能及相关制动安全检测研究[D]. 西安: 长安大学, 2010. ZHAO Kai-hui. Research on Heat Fading of Automobile Brake and Related Brake Safety Inspection[D]. Xi'an:Chang'an University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-11941-2010220150.htm |
| [10] | 王静. 鼓式制动器温升特性台架试验研究[D]. 西安: 长安大学, 2007. WANG Jing. Experimental Study on Temperature Rise Performance of Drum Brake[D]. Xi'an:Chang'an University, 2007. http://d.wanfangdata.com.cn/Thesis/Y1527708 |
| [11] | 纪王芳. 载重汽车行车制动器制动性能的研究[D]. 合肥: 合肥工业大学, 2009. JI Wang-fang. Research on Braking Performance of Service Brakes of Trucks[D]. Hefei:Hefei University of Technology, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10359-2009154823.htm |
| [12] | QC/T 239-2015, 商用车辆行车制动器技术要求及台架试验方法[S]. QC/T 239-2015, Specifications and Bench Test Methods for Commercial Vehicle Service Brake[S]. |
| [13] | 费业泰. 误差理论与数据处理[M]. 北京: 机械工业出版社, 2000. FEI Ye-tai. Error Theory and Data Processing[M]. Beijing: Mechanical Industry Press, 2000. |
| [14] | 赵洪宾. 给水管网系统理论与分析[M]. 北京: 中国建筑工业出版社, 2003. ZHAO Hong-bin. Theory and Analysis of Water Supply Network System[M]. Beijing: China Architecture & Building Press, 2003. |
| [15] | 毛开翼. 关于组合预测中的权重确定及应用[D]. 成都: 成都理工大学, 2007. MAO Kai-yi. Determination and Application of Weight in Combination Forecast[D]. Chengdu:Chengdu University of Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10616-2007142633.htm |
| [16] | 李进. 基于模型优选的风电功率融合预测模型[D]. 太原: 太原理工大学, 2013. LI Jin. Prediction Model for Wind Power Fusion Based on Model Optimization[D]. Taiyuan:Taiyuan University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10112-1013354096.htm |
| [17] | 范永东. 模型选择中的交叉验证方法综述[D]. 太原: 山西大学, 2013. FAN Yong-dong. A Summary of Cross-validation in Model Selection[D]. Taiyuan:Shanxi University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10108-1013325855.htm |
| [18] | 李燕. 基于交叉验证的基本解法求复杂区域边界值问题[D]. 太原: 太原理工大学, 2015. LI Yan. Method of Fundamental Solution with LOOCV for Boundary Value Problems in Complicated Domains[D]. Taiyuan:Taiyuan University of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10112-1015661937.htm |
 2017, Vol. 34
2017, Vol. 34
