扩展功能
文章信息
- 鲍婷婷, 陈建良
- BAO Ting-ting, CHEN Jian-liang
- 交通预测信息对路网流量演化稳定性影响分析
- Analysis on Effect of Traffic Predictive Information on Road Network Traffic Volume Evolution Stability
- 公路交通科技, 2017, 34(7): 121-129
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(7): 121-129
- 10.3969/j.issn.1002-0268.2017.07.017
-
文章历史
- 收稿日期: 2016-09-26
随着现代科技特别是电子通讯技术的发展,智能交通系统(Intelligent Transport Systems, ITS)在世界范围内得到快速的普及应用,用以改善和解决当今存在的诸多城市交通问题。先进的出行者信息系统(Advanced Traveler Information Systems, ATIS)作为ITS的一个核心部分,通过实时向出行者发布交通信息,诱使他们避开拥堵路段而转向通畅的替代路径,从而节约个体出行者的出行时间和费用成本,并从路网整体层面减缓拥堵的形成。显然,为研究ATIS对城市交通的效果,首先需要分析交通信息对出行者选择行为的影响。
交通信息对出行者行为的综合影响可以从出行目的地选择、出行方式选择、出发时间选择及出行路径选择4个方面加以考虑[1, 2]。本研究主要侧重于出行者的路径选择行为分析。在这方面,国内外学者有了广泛的研究工作[3-8]。在现有文献中,交通信息对出行者路径选择行为的效用主要在路网流量均衡状态这一前提假设下进行分析。实际上,城市交通系统不可避免受到OD交通量波动、交通事故、自然灾害等诸多因素的影响,因此,现实的路网流量很难维持在稳定的均衡态,而更多地处于动态波动的非均衡演化过程。“稳定性”概念衡量的是交通系统在受到各种随机因素的影响后,从非均衡状态恢复到稳定均衡状态的能力。考虑到当前很多交通系统规划、设计方案及管理措施都是根据均衡状态这一前提制定的,一个不稳定的交通网络意味着以上方案和措施的效果都会大打折扣,因此对交通系统稳定性的研究具有重要的实用价值和现实意义。
逐日动态演化模型作为交通流量分配的一般性方法,能很好地模拟出路网流量在时间轴上的动态波动过程[9-13]。当前,国内外已有一些研究工作将交通信息对出行者行为的影响考虑进路网交通逐日动态演化过程中。H. J. Huang等[14]在构建的动态模型框架下,分析了出行者对路径选择和对ATIS信息服从率的逐日变动及对ATIS设备购买率的逐年演化过程。G. E. Cantarella[15]针对单一出行者,采用类似的逐日动态模型模拟总用户盈余(Total User Surplus)的演化过程,以此评价ITS对城市交通的效果。刘天亮等[16]在ATIS历史交通信息的影响下,明确考虑了出行者风险规避和认知更新行为,建立了出行者日常择路行为演进模型并分析了其稳定性。郭仁拥等[17]认为ATIS的历史交通信息会存在滞后性问题,因此出行者会根据自己的认识对获取到的交通信息进行一定的调整得到出行者的决策出行费用。刘诗序等[18-19]采用Agent仿真思想,研究了特定的交通信息条件下出行者逐日路径选择行为与系统演化的稳定性,通过对前两天的路径实际发生时间取平均值作为ATIS的路径预测时间信息。
以上研究工作中都未涉及严格意义上的交通预测信息。ATIS在执行交通信息预测的过程中,往往包含了多轮反馈-修正过程,其核心目的是使得ATIS预测的路径出行时间与实际发生的路径行走时间尽量取得一致。这样的反馈-修正机制在一些文献中(如文献[20])也被称为ATIS的预期路线诱导(Anticipatory Route Guidance)问题。ATIS预测性信息能有效地均衡路网流量分布和缓解交通拥堵,同时能避免历史交通信息条件下潜在的出行者过激反应、聚集反应等问题[21]。ATIS提供预测信息的其中一大挑战是保证交通信息的一致性问题:使预测的路径时间与由其影响下实际出行者经历的路径时间保持一致。这需要ATIS能准确预测出行者的路径选择行为。正是由于交通预测信息所包含的复杂性,其对出行者路径选择动态演化的影响作用在目前的文献中还很少得到研究。G. N. Bifulco等[22]将ATIS考虑进路网流量逐日动态演化模型,重点分析了一致性预测信息对路网流量演化收敛性和稳定性的影响。X. M. Lou等[23]在一类离散确定型逐日动态模型中明确考虑了ATIS的一致性预测信息对出行者路径动态调整行为的影响,他们的研究结论表明准确性高的交通预测信息有助于增强路网交通流动态演化的稳定性。
本研究根据非线性动态系统理论,构建一个确定性路网流量逐日演化模型来模拟两类出行者(装备ATIS和未装备ATIS)的路径选择动态调整过程,在此基础上提出一种解析型方法,研究一致性预测信息对路网流量演化稳定性的影响。以一个包含两条平行路径的典型路网为对象进行模型和方法的阐述,该路网被广泛使用于以往文献中[9, 18-19, 24]。在构建的演化模型中,ATIS的交通信息预测过程可看作是一个不动点问题(Fixed Point Problem, FPP),因此预测信息影响下出行者的路径选择结果可通过求解该FPP获得。本研究证明了逐日演化模型的不动点等价于随机用户均衡(Stochastic User Equilibrium, SUE)状态,并证明了在一定条件下该均衡状态满足存在性和唯一性要求。同时,推导出网络交通流演化的渐进稳定性条件。在此基础上,比较分析了交通预测信息对增强路网流量演化稳定性的效果。
2 路网流量逐日演化模型 2.1 出行者经验学习和路径选择过程分析个体出行者关于路径时间的学习更新和路径选择的动态调整是建立路网交通流量演化模型的基础。对未装备ATIS设备的出行者而言,他们对各条备选路径的感知出行时间主要通过对以往出行经验的学习得到。具体而言,出行者进行第t天的路径选择并完成当天的出行后,得到最新一天的出行经验并根据一定的学习机制将其用于更新以往(第t天)的路径感知出行时间,出行者根据更新后的感知结果做出第t+1天的路径选择。
对装备ATIS的出行者而言,他们对备选路径时间费用的感知不再依赖于自身的经验学习,而是通过ATIS的交通信息直接获取。需要注意的是,当ATIS提供的是预测信息时,需要包含一个反馈-调整机制,以满足路径时间预测值与实际值之间的一致性要求。图 1描述了两类出行者在经验学习和路径选择调整过程中的相互作用。

|
| 图 1 出行者经验学习、路径选择逐日演化过程 Fig. 1 Travelers' experience learnings and route choices day-to-day evolution process |
| |
2.2 未装备ATIS的出行者动态模型
考虑由两条平行路径组成的交通网络,如图 2所示,每天的OD交通需求为n。设ATIS设备的市场占有率(即配备ATIS的出行者占总出行者数量的比例)为ρ,则每天未装备ATIS的出行交通量为(1-ρ)n。定义x1(t), x2(t)表示路径1和2在第t天的交通量;C1(t), C2(t)表示未装备ATIS出行者在第t天对路径1和2的感知出行时间;g1(·), g2(·)表示路径1和2的时间阻抗函数。假设各条路径的时间阻抗仅与本路径上的交通流量有关,则路径1和2在第t天的实际出行时间分别为g1(x1(t)), g2(x2(t))。

|
| 图 2 交通网络示意图 Fig. 2 Schematic diagram of traffic network |
| |
为体现出行者对以往出行经验的动态学习更新行为,一种可行的方法是采用指数平滑滤波[10]方法。一方面,该方法简洁直观,符合图 1所示的出行者经验学习行为。另一方面,该方法的数学形式简单,仅包含了单一的学习偏好参数,这种简单性便于数学模型的推导处理以及模型后续的参数校正。另外,指数平滑滤波在当前文献中也得到了比较广泛的应用,并取得了行之有效的结果,这为该方法在论文中的应用提供了理论基础。根据指数平滑滤波法,出行者在第t+1天对路径的感知出行时间可表示为第t天路径感知出行时间和实际发生时间的加权和:
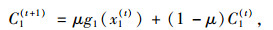
|
(1) |
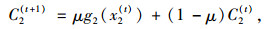
|
(2) |
式中,参数μ(0 < μ≤1) 体现了出行者对前一天路径实际时间和感知时间的偏好,μ值越大,说明出行者更依赖于实际的路径出行时间对路径感知进行更新。
通过出行经验的更新学习,出行者选择感知时间最小的路径完成新一天的出行。在实际情形中,不同出行者之间的感知结果无法达到完全一致,存在一定的感知误差。为此,可以采用Logit随机模型体现出行者每天的路径选择结果。定义p1(t), p2(t)分别表示未装备ATIS的出行者在第t天分别选择路径1和2的概率,根据Logit公式,有:
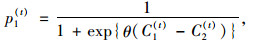
|
(3) |
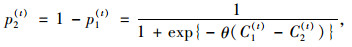
|
(4) |
式中参数θ(θ>0) 体现出行者对路径时间的感知误差程度,θ越大,误差越小。当θ→∞,Logit型随机用户均衡(SUE)趋向于确定用户均衡(Deterministic User Equilibrium, DUE)流量分配。
2.3 装备ATIS的出行者动态模型假设ATIS发布的预测信息满足一致性要求,即预测的路径时间与即将发生的实际路径时间一致。定义S1(t), S2(t)分别表示装备有ATIS的出行者在第t天接收到的关于路径1和2的预测出行时间,在预测信息一致性假设下,S1(t), S2(t)可分别表示为:
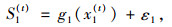
|
(5) |

|
(6) |
式中ε1和ε2分别为ATIS预测信息从发布到出行者接收过程中所引入的随机误差项。假设ε1和ε2相互独立且服从均值为0的Gumbel分布,则装备ATIS的出行者的路径选择结果同样服从Logit随机均衡模型。定义q1(t), q2(t)分别为装备ATIS的出行者在第t天分别选择路径1和2的概率,公式为:

|
(7) |

|
(8) |
其中参数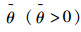
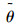
需要注意的是,在式(7)~(8) 中,出行者路径选择概率q1(t),q2(t)取决于当天路径流量分布x1(t)和x2(t),而这又反过来受到q1(t)和q2(t)的影响,因为路网流量是由两类出行者的路径选择结果共同形成的,即:
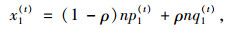
|
(9) |
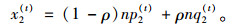
|
(10) |
未装备ATIS的出行者路径选择概率p1(t)和p2(t)可以通过式(3)~(4) 直接确定,则式(7)~(10) 共同定义了一个从(q1(t), q2(t))到它自身的映射,这等价于一个建立在(q1(t), q2(t))上的FPP。
实际上,q1(t)和q2(t)可看作是由FPP式(7)~(10) 所确定的关于p1(t)和p2(t)的隐函数。因此,在根据式(3)~(4) 计算得到p1(t)和p2(t)后,装备ATIS的出行者在第t天的路径选择结果可通过求解该FPP得到。
2.4 包含两类出行者的动态演化模型网络流量逐日演化模型可通过集合前面介绍的两类出行者动态行为得到。定义函数:
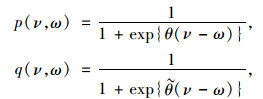
|
(11) |
式中ν和ω分别为任意两条路径的出行时间。
逐日动态交通流演化模型可表示为:
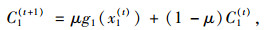
|
(12) |
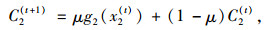
|
(13) |
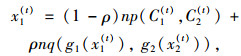
|
(14) |
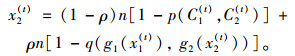
|
(15) |
由2.3节的分析可知,式(14)~(15) 构成了一个(x1(t), x2(t))的FPP,其中x1(t)和x2(t)可看成是关于C1(t)和C2(t)的隐函数。具体的函数关系可通过求解该FPP得到。令G1(·), G2(·)分别表示x1(t)和x2(t)关于C1(t)和C2(t)的函数关系,即:
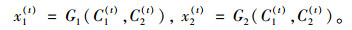
|
(16) |
将x1(t)和x2(t)代入式(12)~(13),得到等价的交通流逐日演化模型为:
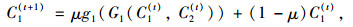
|
(17) |
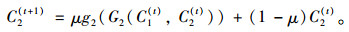
|
(18) |
可以看到,本文所建立的网络交通流演化模型可通过前一天路径感知费用(C1(t), C2(t))到后一天路径感知费用(C1(t+1), C2(t+1))之间的递推关系进行描述。
3 均衡点的存在性、唯一性和稳定性 3.1 模型不动点与流量均衡状态文中所建立的网络交通流量演化模型的不动点与流量均衡状态之间的关系由如下定理给出。
定理1 若逐日演化模型(17)~(18) 的不动点存在,则它等价于包含两类出行者的SUE状态。
证明 模型(17)~(18)(或等价的(12)~(15))的不动点可通过稳定条件C1(t+1)=C1(t)=C1*和C2(t+1)=C2(t)=C2*得到。上标*表示各变量对应的不动点。将上述稳定条件代入式(12)~(13),有C1*=g1(x1*), C2*=g2(x2*)。进一步根据式(14)~(15) 可得到:
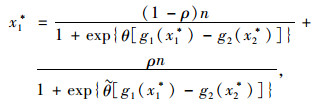
|
(19) |
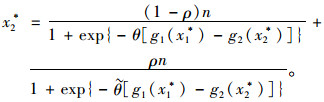
|
(20) |
式(19)~(20) 确切描述了路网中包含两类出行者的SUE状态,定理1得证。
由于模型的不动点与流量均衡状态之间的等价性,因此文中也称之为均衡点。
3.2 均衡点的存在性和唯一性假设1 路径的出行时间阻抗关于路径流量连续可微。
假设2 路径的出行时间阻抗关于路径流量严格单调递增。
定理2 (均衡点存在性)若路径时间阻抗函数满足假设1,则动态模型(17)~(18) 至少存在一个均衡点。
证明 根据Logit路径选择模型,函数p(·), q(·)满足连续性条件。结合假设1,很容易保证由方程(14), (15) 确立的隐函数G1(·)和G2(·)存在且连续。设路径时间阻抗可行集为C,给定路径时间初始值C1(0)和C2(0),集合C是非空有界闭凸集。因此,在均衡点处,动态模型(17)~(18) 本质上是非空闭凸集C到自身的连续映射。根据Brouwer不动点定理,动态模型(17)~(18) 至少存在一个均衡点。
定理3 (均衡点唯一性)若路径时间阻抗函数同时满足假设1和假设2,则动态模型(17)~(18) 存在唯一的均衡点。
证明 根据稳定条件C1(t+1)=C1(t)=C1*和C2(t+1)=C2(t)=C2*,模型(17)~(18) 的均衡点可表示为:C1*=g1(G1(C1*, C2*)), C2*=g2(G2(C1*, C2*)),接下来通过分析函数g1(G1(C1(t), C2(t))), g2(G2(C1(t), C2(t)))关于C1(t)和C2(t)的单调性来验证均衡点的唯一性。注意到∂G1(C1(t), C2(t))/∂C1(t)=∂x1(t)/∂C1(t), ∂G2(C1(t), C2(t))/∂C2(t)=∂x2(t)/∂C2(t)。首先在等式(14) 左右两边同时求C1(t)的偏导,得到方程:
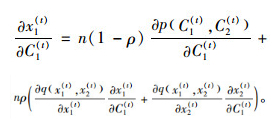
|
(21) |
因为x2(t)=n-x1(t), 所以:
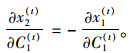
|
(22) |
将式(22) 代入(21) 可求得:
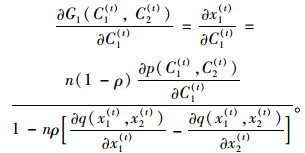
|
(23) |
同理可得:
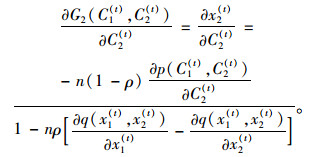
|
(24) |
由于
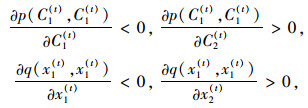
|
(25) |
所以有:
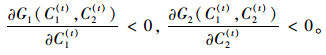
|
(26) |
另外,根据假设2,得到:
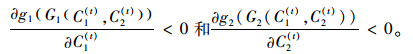
|
(27) |
式(27) 说明函数g1(G1(C1(t), C2(t))), g2(G2(C1(t), C2(t)))分别关于C1(t)和C2(t)严格单调递减,动态模型(17)~(18) 均衡点的唯一性条件满足,定理3得证。
3.3 均衡点的稳定性动态系统的稳定性和渐进稳定性概念都是针对系统的不动点或均衡点而言的。若存在均衡点的某个邻域,使得从属于该领域内的任意初始状态开始,系统的所有后续演化状态都处在该均衡点附近,则称该动态系统的均衡点是稳定的。进一步地,若系统的后续演化状态最终能收敛于该均衡点,则称其是渐进稳定的。
令J*表示动态系统在均衡点处的Jacobian矩阵。根据非线性动态系统理论可知,当矩阵J*的所有特征值都处在单位圆内时,动态系统的均衡点满足渐进稳定性条件。
为便于描述,令
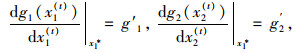
|
(28) |
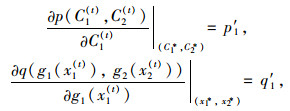
|
(29) |
则有:
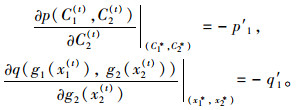
|
(30) |
有关动态系统(17)~(18) 均衡点的渐进稳定条件,有如下定理。
定理4 (均衡点渐进稳定性)动态模型(17)~(18) 均衡点满足渐进稳定的条件是
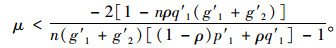
|
(31) |
证明 动态模型(17)~(18) 的Jacobian矩阵为
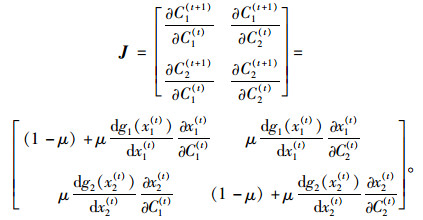
|
(32) |
注意到:

|
(33) |
且
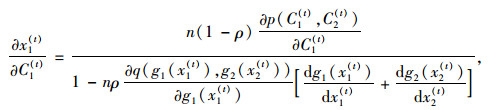
|
(34) |
因此在均衡点处有:
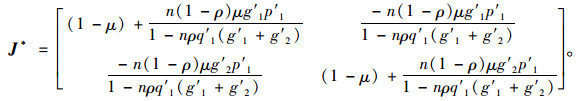
|
(35) |
假设λ1, λ2是J*的两个特征值,容易求得:

|
(36) |
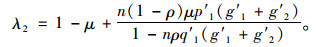
|
(37) |
为保证均衡点的渐进稳定性,需要满足条件:|λ1| < 1, |λ2| < 1。显然,0≤λ1 < 1满足要求。另外,考虑到p′1 < 0, q′1 < 0, g′1>0, g′2>0, 可得到λ2 < 1。因此,只需保证
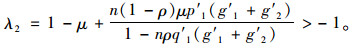
|
(38) |
经过移项得到渐进稳定性条件(31),定理4得证。
3.4 预测信息对稳定性影响分析定理4表明,为保证动态模型(17)~(18) 的均衡点满足渐进稳定条件,出行者的学习偏好参数μ不得大于某一上边界值。当出行者过度依赖于前一天的出行经验对路径感知进行更新时,路网流量将可能变得更不稳定。不等式(31) 右边给出了确切的μ参数上边界值,因此动态模型(17)~(18) 渐进稳定与否可以直接通过验证不等式(31) 进行判定,而不需执行整个模型演化过程。
将参数μ的上边界值看作ρ的函数,记作Φ(ρ),即:
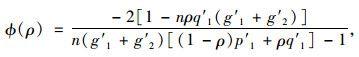
|
(39) |
则式(24) 可简写为:
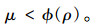
|
(40) |
考虑第1种特殊情况,当ρ=0时,式(40) 可写为:

|
(41) |
式(41) 给出了当路网中所有出行者都没有受到ATIS预测信息影响下,路网流量均衡点的渐进稳定性条件。另一种特殊情形是当路网中几乎所有的出行者都装备有ATIS时,即ρ→1,参数μ的上边界值Φ(1)→2,式(40) 恒成立,这说明当所有出行者都按照一致性预测信息选择路径时,路网交通流量能永远保持渐进稳定的演化过程。
进一步对Φ(ρ)求导,得到:
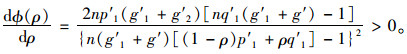
|
(42) |
式(42) 说明随着ATIS使用比例ρ的上升,参数μ的上边界值Φ(ρ)也相应增大,即预测信息的引入,使得出行者可以采用更激进(更大的μ值)的学习机制更新路径时间感知而不致破坏路网交通流量演化的渐进稳定性。以上分析体现了ATIS的路径预测时间信息对路网流量演化稳定性确实具有增强作用。
4 数值仿真试验对图 2所示的交通网络,假设每天的OD交通出行量n=2 000 veh/h, 路径时间阻抗函数服从美国公路局(Bureau of Public Road, BPR)给出的形式:
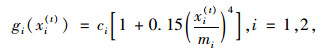
|
(43) |
式中ci, mi分别为路径i的自由流出行时间和设计通行能力,且(c1, c2)=(18 min, 20 min), (m1, m2)=(1 200 veh/h, 1 400 veh/h)。显然,BPR阻抗函数符合3.2节中的假设1和2,因此在本算例中,动态模型(17)~(18) 满足均衡点的存在性和唯一性。假设路网初始流量分布状态为(x1(0), x2(0))=(800 veh/h, 1 200 veh/h),出行者的初始路径感知时间等于路径自由流时间,即(C1(0), C2(0))=(c1, c2)。
为验证第3节的理论分析结果,通过假设不同的μ和ρ参数对动态模型(15)~(16) 进行模拟仿真,模型其他参数设置为:θ=1.2, 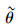

|
| 图 3 不同的ρ和μ影响下路径交通流量演化过程 Fig. 3 Route traffic volume evolution according to different values of ρ and μ |
| |
当路网中有25%比例的出行者根据ATIS的预测信息进行路径选择时,路网流量呈现出不一样的演化趋势,如图 3(b)所示,可求得此时参数μ的上边界值Φ(0.25)=0.7。因此,当μ=0.25或0.60时,路径流量能收敛到SUE均衡点(x1*, x2*)=(1 140.2 veh/h, 859.8 veh/h),而当μ=0.85时,超过了其上边界值,不再满足均衡点的渐进稳定条件,路径流量产生周期波动。
当路网中装备ATIS的出行者比例增长到35%时,参数μ的上边界值进一步增大,此时3类出行者学习偏好参数下路网流量都能收敛到最终的均衡状态,如图 3(c)所示。以上分析说明ATIS提供的一致性交通预测信息对增强路网流量的动态演化稳定性确实具有显著的积极作用。
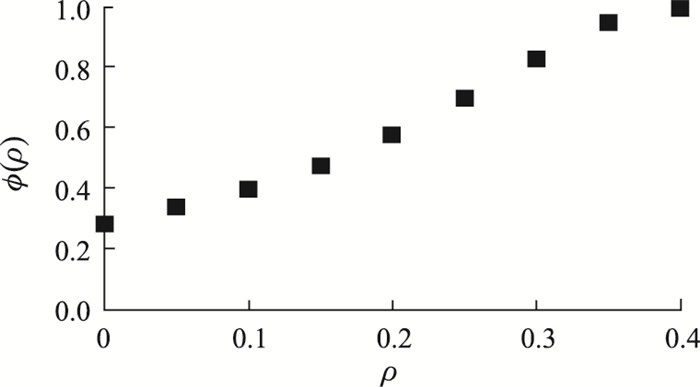
图 4描绘了不同的ρ值对应的上边界值Φ(ρ)。很明显可以看到,Φ(ρ)随着ρ值的增大而增大,这与前面3.4节的理论分析结果一致。另外可以观察到,当ρ≥0.4时,Φ(ρ)≥1,这说明当路网中使用ATIS预测信息的出行者比例超过40%时,则不论出行者的学习偏好参数多大,路网流量都能保持渐进稳定特性并最终收敛于SUE状态。
|
| 图 4 ρ-φ(ρ)关系图 Fig. 4 Relationship between ρ and φ(ρ) |
| |
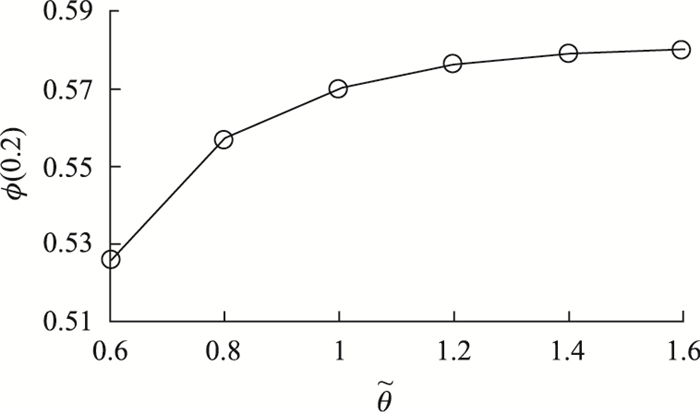
另外,还可以设计额外的数值试验,探究交通预测信息的误差对路网流量演化稳定性的影响。根据前面的分析,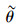
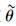
|
图 5 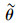 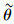 |
| |
可以看出,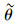
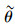
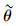
在逐日动态模型的框架下,明确考虑了一致性交通信息预测机制,通过构建一个时间离散的动态交通流量演化系统,模拟了路网中两类出行者(装备ATIS和未装备ATIS)的路径选择动态调整过程。证明了动态演化模型的均衡点等价于SUE状态,并证明了在一定条件下该均衡状态满足存在性和唯一性要求。同时,推导出了网络交通流演化的渐进稳定性条件。通过对稳定性条件的分析,证明了ATIS的预测时间信息对路网流量演化稳定性确实具有增强作用。
分析了ATIS的一致性交通信息预测问题。一致性预测机制能有效提高ATIS交通信息的有效性,避免潜在的出行者过激反应、聚集反应等问题。因此,本研究将对ATIS设备和出行者路径诱导系统的优化完善提供理论基础。另一方面,还系统研究了交通信息对出行者行为模式的影响和效用,这对后续研究ATIS市场经济、优化智能交通系统产业也有一定的借鉴意义。
文中所建立的逐日动态演化模型包含了诸多影响参数,在以后的工作中可以通过实际的路网交通调查数据对这些影响参加进行拟合标定。注意到本研究主要围绕如图 2所示的简单路网展开,因此后续研究可将文中模型和方法扩展到更一般的路网中。另外,文中仅考虑了每天的交通出行需求为固定的情况,未来可以延伸到弹性需求这一情形。同时,模型还可以放松ATIS市场率(即参数ρ)不变这一假设,进一步考虑在市场经济环境下,出行者对ATIS设备的购买与交通预测信息带来的出行时间节约、ATIS设备价格以及出行者的时间价值等因素之间的联动关系。
| [1] | 姜桂艳, 张春勤, 吴正言, 等. 交通信息对出行行为的影响分析综述[J]. 武汉理工大学学报:交通科学与工程版, 2012, 36(3): 450-457 JIANG Gui-yan, ZHANG Chun-qin, WU Zheng-yan, et al. Influence of Traffic Information on Travelers' Behavior:A Literature Review[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2012, 36(3): 450-457 |
| [2] | 李志纯, 黄海军. 先进的旅行者信息系统对出行者选择行为的影响研究[J]. 公路交通科技, 2005, 22(2): 95-99 LI Zhi-chun, HUANG Hai-jun. Modeling the Impacts of Advanced Traveler Information Systems on Travelers' Travel Choice Behaviors[J]. Journal of Highway and Transportation Research and Development, 2005, 22(2): 95-99 |
| [3] | YANG H. Multiple Equilibrium Behaviors and Advanced Traveler Information Systems with Endogenous Market Penetration[J]. Transportation Research Part B:Methodological, 1998, 32(3): 205-218 |
| [4] | YANG H, MENG Q. Modeling User Adoption of Advanced Traveler Information Systems:Dynamic Evolution and Stationary Equilibrium[J]. Transportation Research Part A:Policy & Practice, 2001, 35(10): 895-912 |
| [5] | YANG H, HUANG H J. Modeling User Adoption of Advanced Traveler Information Systems:A Control Theoretic Approach for Optimal Endogenous Growth[J]. Transportation Research Part C:Emerging Technologies, 2004, 12(¾): 193-207 |
| [6] | LO H K, SZETO W Y. A Methodology for Sustainable Traveler Information Services[J]. Transportation Research Part B:Methodological, 2002, 36(2): 113-130 |
| [7] | YIN Y, YANG H. Simultaneous Determination of the Equilibrium Market Penetration and Compliance Rate of Advanced Traveler Information Systems[J]. Transportation Research Part A:Policy and Practice, 2003, 37(2): 165-181 |
| [8] | HUANG H J, LI Z C. A Multi-class, Multi-criteria Logit-based Traffic Equilibrium Assignment Model under ATIS[J]. European Journal of Operational Research, 2007, 176(3): 1464-1477 |
| [9] | HOROWITZ J L. The Stability of Stochastic Equilibrium in a Two Link Transportation Network[J]. Transportation Research Part B:Methodological, 1984, 18(1): 13-28 |
| [10] | CANTARELLA G E, CASCETTA E. Dynamic Processes and Equilibrium in Transportation Networks:Towards a Unifying Theory[J]. Transportation Science, 1995, 29(4): 305-329 |
| [11] | WATLING D P, CANTARELLA G E. Modelling Sources of Variation in Transportation Systems:Theoretical Foundations of Day-to-day Dynamic Models[J]. Transportmetrica B:Transport Dynamics, 2013, 1(1): 3-32 |
| [12] | CANTARELLA G E, WATLING D P. A General Stochastic Process for Day-to-day Dynamic Traffic Assignment:Formulation, Asymptotic Behavior, and Stability Analysis[J]. Transportation Research Part B:Methodological, 2016, 92: 3-21 |
| [13] | LOU X, CHENG L. Travelers' Risk-taking Behaviors in Day-to-day Dynamic Evolution Model[J]. Transportation Research Record, 2016, 2565: 27-36 |
| [14] | HUANG H J, LIU T L, YANG H. Modeling the Evolutions of Day-to-day Route Choice and Year-to-year ATIS Adoption with Stochastic user Equilibrium[J]. Journal of Advanced Transportation, 2008, 42(2): 111-127 |
| [15] | CANTARELLA G E. Day-to-day Dynamic Models for Intelligent Transportation Systems design and Appraisal[J]. Transportation Research Part C:Emerging Technologies, 2013, 29(1): 117-130 |
| [16] | 刘天亮, 黄海军, 陈剑. 考虑风险规避和认知更新的日常择路行为演进[J]. 交通运输工程学报, 2008, 8(4): 90-103 LIU Tian-liang, HUANG Hai-jun, CHEN Jian. Evolution of Day-to-day Route Choice Behavior Considering Risk Aversion and Perception Updating[J]. Journal of Traffic and Transportation Engineering, 2008, 8(4): 90-103 |
| [17] | 郭仁拥, 黄海军. ATIS环境下交通配流的动态演化模型[J]. 管理科学学报, 2008, 11(2): 12-19 GUO Ren-yong, HUANG Hai-jun. Dynamical Evolutionary Model of Traffic Assignment under ATIS[J]. Journal of Management Sciences in China, 2008, 11(2): 12-19 |
| [18] | 刘诗序, 关宏志, 严海. 交通信息对驾驶员逐日路径选择行为影响研究[J]. 武汉理工大学学报:交通科学与工程版, 2011, 35(6): 1130-1134 LIU Shi-xu, GUAN Hong-zhi, YAN Hai. Research on the Influence of Traffic Information on Drivers' Day-to-day Route Choice Behavior[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2011, 35(6): 1130-1134 |
| [19] | 刘诗序, 关宏志, 严海. 预测信息下的驾驶员逐日路径选择行为与系统演化[J]. 北京工业大学学报, 2012, 38(2): 269-274 LIU Shi-xu, GUAN Hong-zhi, YAN Hai. Drivers' Day-to-day Route Choice Behavior and System Evolution under Forecast Information[J]. Journal of Beijing University of Technology, 2012, 38(2): 269-274 |
| [20] | BOTTOM J A. Consistent Anticipatory Route Guidance[D]. Cambridge:Massachusetts Institute of Technology, 2000. |
| [21] | 张存保, 杨晓光, 严新平. 交通信息对驾驶员选择行为的影响研究[J]. 交通与计算机, 2004, 22(5): 31-34 ZHANG Cun-bao, YANG Xiao-guang, YAN Xin-ping. The Effect of Travel Information on Drivers' Choice[J]. Computer and Communications, 2004, 22(5): 31-34 |
| [22] | BIFULCO G N, CANTARELLA G E, SIMONELLI F, et al. Advanced Traveler Information Systems under Recurrent Traffic Conditions:Network Equilibrium and Stability[J]. Transportation Research Part B:Methodological, 2016, 92: 73-87 |
| [23] | LOU X M, CHENG L, CHU Z M. Modelling Travellers' En-route Path Switching in a Day-to-day Dynamical System[J]. Transportmetrica B:Transport Dynamics, 2017, 5(1): 17-41 |
| [24] | 刘诗序, 关宏志, 严海. 网络交通流动态演化的混沌现象及其控制[J]. 物理学报, 2012, 61(9): 58-67 LIU Shi-xu, GUAN Hong-zhi, YAN Hai. Chaotic Behavior in the Dynamical Evolution of Network Traffic Flow and Its Control[J]. Acta Physica Sinica, 2012, 61(9): 58-67 |
 2017, Vol. 34
2017, Vol. 34
