扩展功能
文章信息
- 郑来, 何莎莉
- ZHENG Lai, HE Sha-li
- 高速公路大区段交通事故预测模型研究
- Study on Traffic Accident Prediction Model for Long Sections of Expressway
- 公路交通科技, 2017, 34(7): 108-114
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(7): 108-114
- 10.3969/j.issn.1002-0268.2017.07.015
-
文章历史
- 收稿日期: 2016-08-30
截至2014年年底,我国高速公路通车里程达到11.2万km,位居世界第一,这为全面推进“一带一路”战略的实施打下了坚实的基础。然而,高速公路的交通安全形势却不容乐观,每年都导致大量的人员伤亡和巨额的财产损失。加强高速公路交通安全研究,对改善高速公路交通安全水平具有十分重要的作用。其中,交通事故预测模型是高速公路交通安全研究的一个重要方面,为高速公路事故多发路段突出影响因素的识别和安全改善对策的制订等提供了基础工具。
高速公路交通事故预测模型可以分为宏观和微观两种,其中微观模型的作用是通过建模来分析基本路段上的事故数(率)与路段相关变量(道路、交通、环境条件)之间的关系。常见的微观模型包括Poisson回归模型[1]、负二项回归模型[1]、零堆积Poisson回归模型[2]、零堆积负二项回归模型[3]等参数化模型和模糊逻辑预测模型[4]、神经网络预测模型[5]、支持向量机预测模型[6]等非参数化模型。建立微观交通事故预测模型的先决条件是进行基本路段划分[7]。国内外学者提出了多种基本路段划分方法,比如定长法、基于几何线形指标不可再分的路段划分方法、基于事故聚类分析的路段划分方法等,这些方法所划分的路段长度一般较短[8-10]。由于事故发生过程的动态性和连续性,事故发生的起始点和终止点间通常有一定的间距。因此,在传统的短路段划分背景下,记录的事故发生地点与诱发事故的变量指标之间可能不能很好地匹配。比如,长大下坡接平曲线路段,记录的发生在平曲线上的交通事故可能是由于大下坡路段上的车速过高引起的。如果根据事故发生地点简单分析平曲线路段上的交通事故与平曲线线形指标的关系,很可能导致错误的分析结论。陈斌等人的研究就表明,在连续大下坡路段上,事故率与事故发生地点前2 km以上路段的平均纵坡显著相关[11]。再者,现行的交通事故位置记录精度也要求路段划分不能过短。通常是不低于100 m,国外则要求一般不低于0.16 km[12-14]。
为了降低因过短或不合理的路段划分带来的交通事故预测方面的分析结论偏差,本研究提出利用高速公路上的天然节点(互通式立交和服务区)进行大区段划分,并尝试构建高速公路大区段交通事故预测模型。
1 大区段划分及数据描述 1.1 大区段划分大区段是高速公路上具有交通量均质性和交通流连续性的较长路段,一般指利用高速公路上的互通式立交、服务区等天然节点划分得到的路段。大区段的划分示意如图 1所示。具体而言,以两个相邻的互通式立交为例,其所界定的大区段是指某行车方向上始于前一立交加速车道终点止于下一立交减速车道起点的路段。在大区段条件下,由于互通式立交、服务区等的分隔作用,本区段上的交通事故一般仅可能与当前区段的道路、交通、环境因素有关,不会受到邻近区段相关因素的影响。
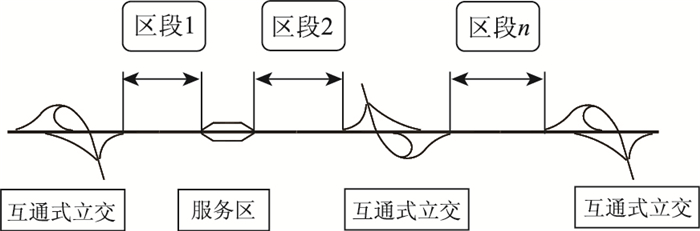
|
| 图 1 大区段划分 Fig. 1 Division of long sections |
| |
1.2 数据描述
依托辽宁省交通厅科技项目《高速公路运行安全研究》,收集了辽宁省境内的沈大高速、沈山高速、沈丹高速、沈康高速和铁阜高速5条高速公路2009年至2012年的道路交通条件数据和交通事故数据。
道路交通条件数据主要来自于各条高速公路的设计文件、交通量流量报表和现场调查时拍摄的行车记录仪视频,具体包括平纵线形指标、填挖方路段分布、交通量和沿线交通设施设置情况。根据设计文件,划分各条高速公路的大区段结果如表 1所示。5条高速公路共被划分成67个大区段,平均区段长度为13.987 km,最小长度为0.824 km,最大长度为35.110 km。
| 总里程/ km |
大区段 数量* |
大区段长度/km | 事故总 数/次 |
|||
| 平均值 | 最小值 | 最大值 | ||||
| 沈大高速 | 252.653 | 27 | 9.358 | 2.160 | 20.960 | 4 173 |
| 沈山高速 | 238.709 | 18 | 13.262 | 2.650 | 30.050 | 2 909 |
| 沈丹高速 | 125.744 | 8 | 15.718 | 0.824 | 28.800 | 764 |
| 沈康高速 | 52.871 | 3 | 17.624 | 4.850 | 29.023 | 240 |
| 铁阜高速 | 153.727 | 11 | 13.975 | 1.540 | 35.110 | 1 759 |
| 注:表中数据为实际采用的里程和大区段数量,部分区段因事故数据缺失而未被采用。 | ||||||
交通事故数据来自于高速公路的路政管理部门,共收集到2009年至2012年4年的交通事故记录。剔除发生在互通式立交、服务区范围内的交通事故后,得到在大区段上的交通事故9 845次。各条高速公路的交通事故数见表 1。
2 模型变量选择与处理交通事故的发生是人、车、路、环境4个因素共同作用的结果。本文结合所掌握的数据,从车、路、环境3个方面选择模型变量。其中,车的因素选择了年平均日交通量(AADT);路的因素方面选择了路段长度、平面线形指标、纵断面线形指标和标志设置;环境因素方面则考虑了挖方路段可能给交通事故发生带来的影响。
在大区段划分的条件下,同一路段上除AADT相同外,其他变量都存在一定的异质性。比如,一个大区段包含了半径不同的多个圆曲线或竖曲线,同一区段上挖方段长度和位置也各不相同。为了更好地将这些变量融入交通事故预测模型构建过程中,需要对具有异质性的变量进行处理。
(1) 平面线形指标
对平面线形而言,一般考虑圆曲线的半径、长度对交通事故发生的影响[15-16]。以这两个指标为基础,定义了累积曲率指标,其计算公式为:

|
(1) |
式中,CURi为区段i的累积曲率;Lcij为区段i上第j个圆曲线的长度;Rij为区段i上第j个圆曲线的半径;Li为第i个区段的长度。经计算,67个大区段的累积曲率的最小值、平均值和最大值依次为0, 0.161, 0.595 km-1。
(2) 纵断面线形指标
对纵断面线形而言,一般认为纵坡的坡度、坡长等对交通事故的发生有较大影响[15-16]。结合这两个指标,定义了累积纵坡指标,其计算公式为:
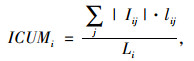
|
(2) |
式中,ICUMi为区段i的累积纵坡;Iij为区段i上第j个纵坡的坡度;lij为区段i上第j个纵坡的坡长。经计算,67个大区段的累积纵坡度的最小值、平均值和最大值依次为0.118%, 0.865%, 2.436%。
(3) 挖方路段
挖方边坡是一种常见的引发交通事故的路侧障碍物[17],同时也可能对驾驶员视距产生影响。考虑到道路挖方对交通安全的影响,引入挖方路段比例指标,其计算公式为:
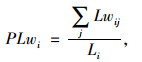
|
(3) |
式中,PLwi为区段i的挖方路段比例;Lwij为区段i上第j个挖方段长度。经计算,67个大区段的挖方路段比例的最小值、平均值和最大值依次为0, 0.135, 0.471。
(4) 交通标志
交通标志是保障道路安全、顺畅的重要设施。但其设置数量的多少会导致信息不足或过载,从而影响交通安全。为此,引入交通标志密度指标,其计算公式为:
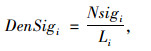
|
(4) |
式中,DenSigi为区段i的交通标志密度;Nsigi为区段i上的标志数量。经计算,67个大区段的交通标志密度比例的最小值、平均值和最大值依次为0, 1.624, 6.481个/km。
3 模型变量的模块确定高速公路基本路段交通事故预测模型的基本形式为:
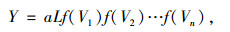
|
(5) |
式中,Y为某路段上的期望事故数;a为模型常数;L为路段长度;V1,V2, …,Vn为其他模型变量;f(·)为变量在事故预测模型中存在的函数形式,又被称为变量模块。
3.1 模块构建方法在大区段划分的背景下,各变量所对应的模块形式并不能根据经验确定,因此引入积分-微分(Integrate-Differentiate,ID)方法进行模块形式的确定[18]。该方法的核心思想是利用变量X的经验积分函数FE(X)来确定模块f(X)的形式。
以变量AADT为例,ID方法的具体步骤为:(1) 确定区段i的基础事故率,即将该区段n年的事故数除以区段长度,目的是消除区段长度对模块形式确定的影响;(2) 确定AADT的各区间宽度。将各区段的AADT按升序排列,任意一个AADT的区间宽度为与当前AADT相邻的两个AADT的差值除以2;(3) 确定AADT的各区间高度,即为当前AADT所对应的事故率。如果一个AADT对应多个事故率,则取其平均值;(4) 确定经验积分函数在某AADT区间的累积值,该值为所有AADT小于当前AADT的区间的事故率总和;(5) 结合AADT和对应累积值的散点分布,进行曲线拟合,即可得到经验积分函数FE(AADT);对该函数求导,即可得到AADT所对应的模块形式,即f(AADT)=F′E(AADT)。
3.2 模块确定结果按照上述方法,得到AADT,CUR,ICUM,PLw和DenSig这5个变量的散点分布图。采用最小二乘曲线拟合方法,尝试幂函数、指数函数和Hoerl函数3种形式,拟合优度通过决定系数R2来判断。各种函数形式的拟合优度结果如表 2所示。
| 变量 | 幂函数 [α/(β+1)]Xβ+1 |
指数函数 [α/β]eβX |
Hoerl函数 α[eβX(βX-1)/β2+1/β2] |
| AADT | 0.963 | 0.896 | 0.965 |
| CUR | 0.820 | 0.536 | — |
| ICUM | 0.957 | 0.771 | 0.974 |
| PLw | 0.841 | 0.987 | — |
| DenSig | 0.935 | 0.722 | 0.980 |
| 注:“—”表示最小二乘估计不存在;α和β为模块参数。 | |||
由表 2对比结果可知,不同变量所对应的模块形式各不相同。其中,AADT,ICUM和DenSig应采用Hoerl函数形式,即f(X)=αXeβX;CUR应采用幂函数形式,即f(X)=αXβ;而PLw应采用指数函数形式,即f(X)=αeβX。各变量模块最优函数的拟合情况如图 2所示。
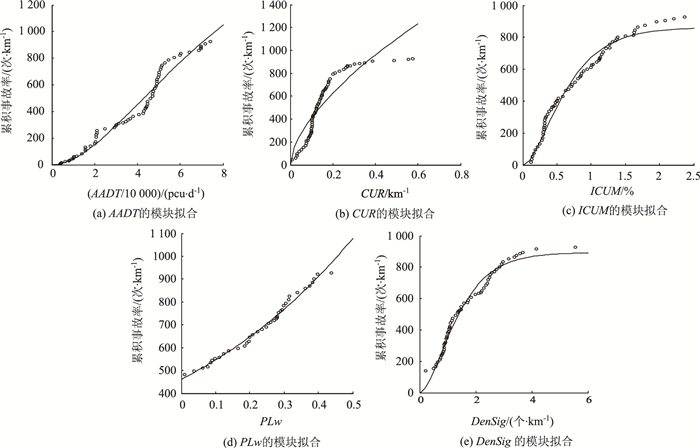
|
| 图 2 模块的最优函数拟合 Fig. 2 Best function fitting for blocks |
| |
4 事故预测模型构建 4.1 负二项回归方法
负二项回归模型是在交通事故预测中较为常用的一种广义线性回归分析模型,其结构为:
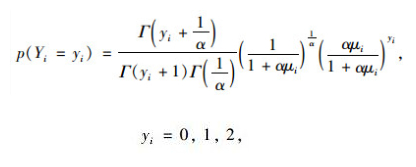
|
(6) |
式中,Yi和yi为区段i上发生交通事故的次数;α为离散度指数;μi为区段i上发生交通事故数的期望值;Γ(·)为伽马函数。
根据最优模块的分析结果,μ的初始结构形式为:
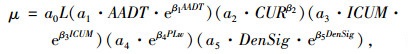
|
(7) |
式中,a0,a1,a2,a3,a4,a5,β0,β1,β2,β3,β4和β5均为模型参数。
4.2 模型比选为分析变量及相应模块引入对事故预测模型的影响,采用逐步分析方法,即将变量模块依次引入事故预测模型中,并利用极大似然估计方法进行模型参数估计,最后根据标定模型的似然度选择最优模型。各模块逐步分析的结果见表 3。
| 模型 | 常数 | ln L | ln(AADT/10 000) | AADT/10 000 | ln CUR | ln ICUM | ICUM | PLw | ln DenSig | DenSig | 逻辑似然度 |
| 1 | 3.021 | 0.823 | — | — | — | — | — | — | — | — | -703.126 |
| 2 | 2.686 | 0.870 | 0.903 | -0.216 | — | — | — | — | — | — | -664.92 |
| 3 | 2.619 | 0.877 | 0.900 | -0.220 | -0.030 | — | — | — | — | — | -664.065 |
| 4 | 2.654 | 0.851 | 0.817 | -0.204 | — | -0.174 | 0.054 | — | — | — | -658.055 |
| 5 | 2.761 | 0.882 | 0.835 | -0.202 | — | — | — | -0.612 | — | — | -639.978 |
| 6 | 2.490 | 0.845 | 0.686 | -0.094 | — | — | — | — | -0.064 | -0.014 | -633.018 |
| 7 | 2.419 | 0.855 | 0.685 | -0.097 | -0.021 | — | — | — | -0.065 | -0.006 | -632.407 |
| 8 | 1.936 | 0.837 | 0.552 | -0.064 | — | -0.444 | 0.453 | — | -0.075 | 0.004 | -614.236 |
| 9 | 2.528 | 0.862 | 0.641 | -0.089 | — | — | — | -0.057 | -0.065 | -0.002 | -627.660 |
| 10 | 1.978 | 0.825 | 0.543 | -0.058 | 0.025 | -0.478 | 0.483 | -0.075 | -0.006 | -613.268 | |
| 11 | 2.506 | 0.864 | 0.641 | -0.090 | -0.006 | — | — | -0.494 | -0.065 | 0.003 | -627.606 |
| 注:“—”表示模型未使用该变量。 | |||||||||||
由表 3可知,拟合优度最好的是模型10,逻辑似然度为-613.268,该模型包括了L,AADT,CUR,ICUM和DenSig这5个变量;模型8的拟合优度仅次于模型10,逻辑似然度为-614.236,该模型包括了L,AADT,ICUM和DenSig这4个变量。相较于模型8,模型10在多引入1个变量的情况下,逻辑似然度仅提高了0.968。从模型复杂度和拟合优度平衡的角度考虑,最终确定模型8为最优模型。
具体的最优模型的参数估计结果见表 4。由各变量的显著性分析可知,在大区段划分的条件下,高速公路交通事故的发生主要受到路段长度、交通量、纵坡和交通标志密度等因素的显著影响。相较而言,平面线形和道路挖方对交通事故的影响则并不显著,这可能是所使用的辽宁省高速公路数据的平面线形和地形特点较为单一所致。
| 估计值 | 标准差 | z值 | p值 | |
| 常数 | 1.936 | 0.231 | 8.367 | < 2e-16 |
| ln L | 0.837 | 0.045 | 18.614 | < 2e-16 |
| AADT/10 000 | -0.064 | 0.042 | -1.516 | 0.129 |
| ln(AADT/10 000) | 0.552 | 0.112 | 4.928 | 8.33e-07 |
| ICUM | 0.453 | 0.142 | 3.186 | 0.001 |
| ln ICUM | -0.444 | 0.106 | -4.193 | 2.75e-05 |
| DenSig | 0.004 | 0.035 | 0.050 | 0.959 77 |
| ln DenSig | -0.075 | 0.012 | -6.220 | 4.99e-10 |
4.3 模型变量影响分析
根据模型标定结果,得到高速公路大区段上的期望事故数为:

|
(8) |
例如,某区段的L=2.760 km,AADT=21020 pcu/d,ICUM=0.623%,DenSig=2.899个/km,则该区段的期望事故数为32.4次。
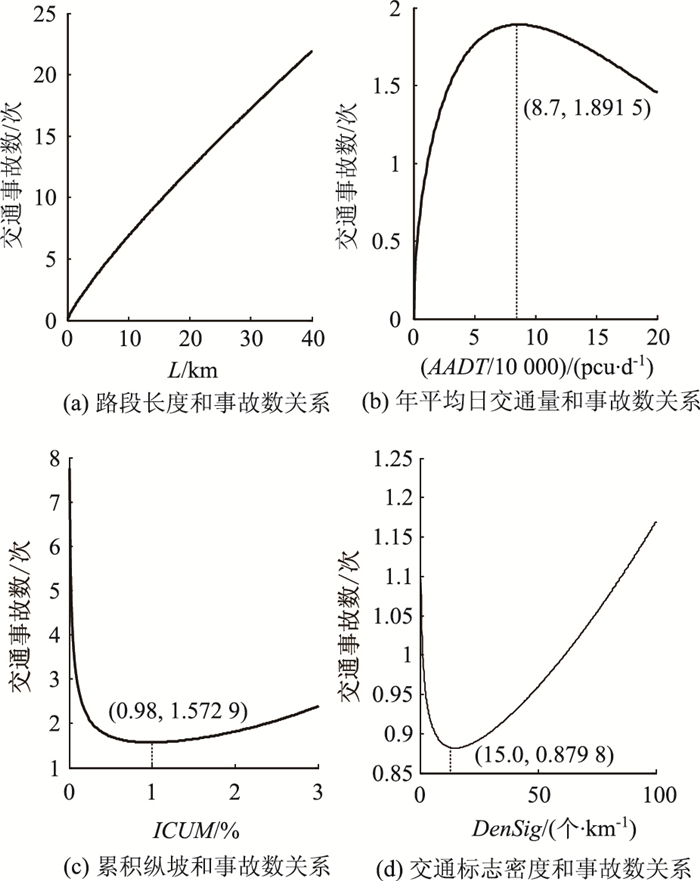
假设其他变量不变,逐一分析交通事故数与其中任一变量之间的关系,结果如图 3所示。
|
| 图 3 交通事故数与各变量之间的关系 Fig. 3 Relationship between traffic accident frequency and different variables |
| |
由图 3可知:
(1) 交通事故与区段长度之间呈非线性的单调递增关系,即随着区段长度的增加,该区段上的交通事故数也会逐渐增多。
(2) 在高速公路通行能力范围内,随着交通量的增加,对应区段的交通事故数也逐渐增加;当交通量大于约8.7万pcu时,高速公路逐渐饱和。此时,交通状态属于稳定车流、强制车流或冻结车流,车辆将保持低速顺序通行,交通事故数也将有所降低,但降低幅度总体较小。
(3) 交通事故数与累积纵坡之间呈现非线性凹形曲线关系,当大区段的累积纵坡接近1%时,交通事故数最低;当累积纵坡小于1%时,较小的坡度或较短的坡长对车辆速度限制较小,而较高的车速则会导致交通事故风险的增加;当累积纵坡大于1%时,随着纵坡坡度或坡长的增加,大小型车车速差逐渐加大,车速的离散化会在一定程度上导致交通事故数的上升。
(4) 交通事故数与交通标志密度之间也呈现非线性凹形曲线关系。当标志密度小于15个/km时,随着标志数量的增加,其所提供的指示、警告等信息更加完善,将在一定程度上避免交通事故的发生;当标志密度大于15个/km时,随着标志数量的增加,交通事故数则逐渐增多,这可能是由于信息过载所引起的。
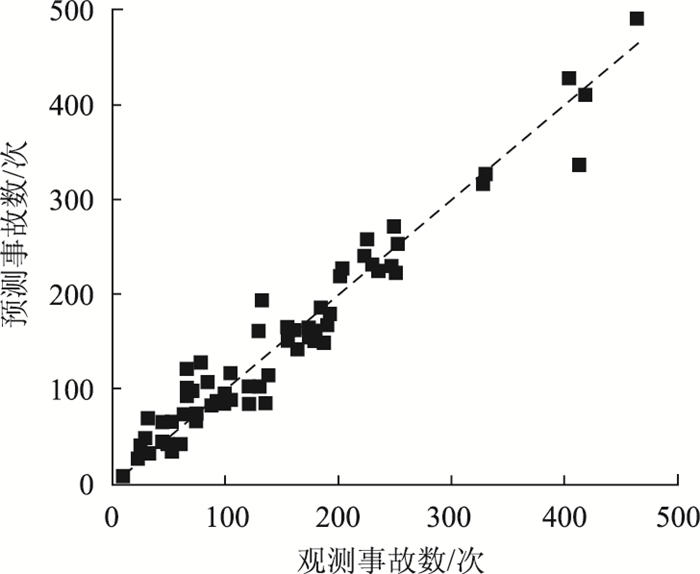
4.4 模型预测精度分析最优模型的预测事故数与观测事故数的对比如图 4所示。模型预测精度较高,预测事故数和观测事故数的散点基本分布在斜率为1的直线左右。由计算可知,观测事故数和预测事故数的平均相对误差为-0.01,平均绝对误差为18.24%。
|
| 图 4 预测事故数与观测事故数对比 Fig. 4 Comparison between predicted traffic accident frequency and observed traffic accident frequency |
| |
5 结论
在大区段划分的条件下,探讨了高速公路交通事故预测模型的构建方法,取得了以下研究成果:
(1) 提出了对区段内变量指标存在的异质性进行处理的方法,构建了累积曲率(CUR)、累积纵坡(ICUM)、挖方段比例(PLw)和标志密度(DenSig)等模型变量。
(2) 引入了ID方法,识别出了AADT,CUR,ICUM,PLw和DenSig等变量的模块结构。其中,AADT,ICUM和DenSig应采用Hoerl函数形式,CUR应采用幂函数形式,而PLw应采用指数函数形式。
(3) 采用负二项回归方法,建立了大区段条件下的交通事故预测模型。模型比选结果表明,路段长度、交通量、纵坡和标志密度等因素对大区段交通事故发生具有显著影响。此外,模型预测事故数也具有较高的精度。
本研究为高速公路交通事故预测提供了新思路,也为模型变量处理、变量模块形式确定等提供了方法支撑。然而,由于本文所使用的数据均来自于辽宁省高速公路,所识别的突出影响因素和相关因素建议值是否具有普适性仍有待验证。未来将考虑更为全面的、适用于大区段条件的交通事故影响因素(如挖方深度、横断面指标、气候条件等),同时也将收集更为丰富的数据对所确定的显著模型变量、模型预测精度以及模型的普适性等进行进一步分析。此外,面向大区段的交通事故预测模型主要适用于中观水平的安全分析与评价,在解释某具体指标(如某平曲线半径、某个标志)对交通事故发生影响方面具有局限性。
| [1] | MIAOU S P. The Relationship between Truck Accidents and Geometric Design of Road Sections:Poisson versus Negative Binomial Regressions[J]. Accident Analysis and Prevention, 1994, 26(4): 471-482 |
| [2] | EI-BASYOUNY K, SAYED T. Comparison of Two Negative Binomial Regression Techniques in Developing Accident Prediction Models[J]. Transportation Research Record, 2006, 1950: 9-16 |
| [3] | LORD D, WASHINGTON S P, IVAN J N. Poisson, Poisson-gamma and Zero Inflated Regression Models of Motor Vehicle Crashes:Balancing Statistical Fit and Theory[J]. Accident Analysis and Prevention, 2005, 37(1): 35-46 |
| [4] | 孟祥海, 郑来, 秦观明. 基于模糊逻辑的交通事故预测及影响因素分析[J]. 交通运输系统工程与信息, 2009, 9(2): 87-92 MENG Xiang-hai, ZHENG Lai, QIN Guan-ming. Traffic Accidents Prediction and Prominent Influencing Factors Analysis Based on Fuzzy Logic[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(2): 87-92 |
| [5] | 李娟, 邵春福. 基于BP神经网络的交通事故预测模型[J]. 交通与计算机, 2006, 24(2): 34-37 LI Juan, SHAO Chun-fu. Traffic Accident Forecast Model Based on BP Neural Network[J]. Computer and Communications, 2006, 24(2): 34-37 |
| [6] | DONG N, HUANG H L, ZHENG L. Support Vector Machine in Crash Prediction at the Level of Traffic Analysis Zones:Assessing the Spatial Proximity Effects[J]. Accident Analysis and Prevention, 2015, 82: 192-198 |
| [7] | 马壮林, 邵春福, 胡大伟, 等. 高速公路交通事故起数时空分析模型[J]. 交通运输工程学报, 2012, 12(2): 93-99 MA Zhuang-lin, SHAO Chun-fu, HU Da-wei, et al. Temporal-spatial Analysis Model of Traffic Accident Frequency on Expressway[J]. Journal of Traffic and Transportation Engineering, 2012, 12(2): 93-99 |
| [8] | 孟祥海, 侯芹忠, 史永义. 基于线形指标的山岭重丘区高速公路事故预测模型[J]. 公路交通科技, 2014, 31(8): 138-143 MENG Xiang-hai, HOU Qin-zhong, SHI Yong-yi. An Accident Prediction Model for Expressway in Mountainous Hilly Area Based on Alignment Indexes[J]. Journal of Highway and Transportation Research and Development, 2014, 31(8): 138-143 |
| [9] | LU J Y, GAN A, HALEEM K, et al. Clustering-based Roadway Segment Division for the Identification of High-crash Locations[J]. Journal of Transportation Safety & Security, 2013, 5(3): 224-239 |
| [10] | 孟祥海, 李梅, 麦强, 等. 高速公路事故多发点鉴别及诱发因素识别[J]. 交通运输系统工程与信息, 2011, 11(1): 114-120 MENG Xiang-hai, LI Mei, MAI Qiang, et al. Research on Identification of Black Spot and Accident Inducing Factor for Freeway[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(1): 114-120 |
| [11] | 陈斌, 袁伟, 付锐, 等. 连续长大下坡路段交通事故特征分析[J]. 交通运输工程学报, 2009, 9(4): 75-78, 84 CHEN Bin, YUAN Wei, FU Rui, et al. Analysis of Traffic Accident Characteristic on Continuous Long Downgrade Section[J]. Journal of Traffic and Transportation Engineering, 2009, 9(4): 75-78, 84 |
| [12] | CHANG L Y. Analysis of Freeway Accident Frequencies:Negative Binomial Regression versus Artificial Neural Network[J]. Safety Science, 2005, 43(8): 541-557 |
| [13] | YU R J, ABDEL-ATY M, AHMED M. Bayesian Random Effect Models Incorporating Real-time Weather and Traffic Data to Investigate Mountainous Freeway Hazardous Factors[J]. Accident Analysis and Prevention, 2013, 50(2): 371-376 |
| [14] | HALEEM K, GAN A. Effect of Driver's Age and Side of Impact on Crash Severity along Urban Freeways:A Mixed Logit Approach[J]. Journal of Safety Research, 2013, 46: 67-76 |
| [15] | 孟祥海, 张晓明, 郑来. 基于线形与交通状态的山区高速公路追尾事故预测[J]. 中国公路学报, 2012, 25(4): 113-118 MENG Xiang-hai, ZHANG Xiao-ming, ZHENG Lai. Prediction of Rear-end Collision on Mountainous Expressway Based on Geometric Alignment and Traffic Conditions[J]. China Journal of Highway and Transport, 2012, 25(4): 113-118 |
| [16] | 孟祥海, 覃薇, 邓晓庆. 基于神经网络的山岭重丘区高速公路事故预测模型[J]. 公路交通科技, 2016, 33(3): 102-108 MENG Xiang-hai, QIN Wei, DENG Xiao-qing. An Accident Prediction Model for Expressways in Mountainous and Rolling Areas Based on Neural Network[J]. Journal of Highway and Transportation Research and Development, 2016, 33(3): 102-108 |
| [17] | 谢来发. 高速公路路侧事故分析与安全保障技术研究[D]. 西安: 长安大学, 2012. XIE Lai-fa. Analysis on Freeway Roadside Accidents and Research on Safety Security Techniques[D]. Xi'an:Chang'an University, 2012. |
| [18] | HAUER E, BAMFO J. Two Tools for Finding What Function Links the Dependent Variable to the Explanatory Variables[C]//ICTCT Workshops. Lund:[s.n.], 1997. |
 2017, Vol. 34
2017, Vol. 34
