扩展功能
文章信息
- 谢晓锋, 吴秋红, 刘恺
- XIE Xiao-feng, WU Qiu-hong, LIU Kai
- 考虑孔隙水压力影响的深埋盾构隧道开挖面稳定性分析
- Analysis on Excavation Face Stability of Deep Shield Tunnel Considering Effect of Pore Water Pressure
- 公路交通科技, 2017, 34(7): 94-100
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(7): 94-100
- 10.3969/j.issn.1002-0268.2017.07.013
-
文章历史
- 收稿日期: 2016-03-16
在盾构隧道的掘进过程中,开挖面前方围岩的原始平衡状态受到扰动,将产生较大的变形并发生破坏,不仅严重威胁隧道内工作人员的生命安全,还会造成工程项目重大财产损失。因此,研究盾构隧道开挖面的稳定性问题,对实际工程项目建设有显著的科学价值和现实意义[1-4]。
隧道开挖面的稳定性是一个极其复杂的问题,包括围岩等级、地下水、开挖断面大小以及开挖方式等在内的众多因素都对其有较大的影响。Davis等[5]最早采用极限分析理论对隧道开挖面的稳定性进行分析,并得到了无黏性土体中隧道开挖面在不同情况下的极限支护压力。Chambon和Corte[6]采用离心试验法对浅埋隧道开挖面的稳定性进行了研究,结果表明开挖面的破坏可近似用一旋转破坏机制描述。Leca和Dormieux[7]提出了隧道开挖面的圆锥体破坏机制,并通过对比支护力上限解与离心试验数据,验证了这一机制的有效性。随后,Soubra[8]以及Mollon等[9]构建了多块体旋转破坏机制,并通过极限分析计算得到了更加接近于离心试验结果的支护力。Mollon等[10-11]基于空间离散技术改进了前人所提出的破坏机制,并通过与已有文献中的计算结果进行对比,证明了其所构建机制的优越性。Subrin和Wong[12]根据离心试验所得的破坏形状,构建了隧道开挖面的双对数螺旋曲线破坏机制,计算结果表明这一破坏机制优于多块体旋转破坏机制。
然而,现有文献中关于地下水影响下盾构隧道开挖面稳定性的研究则相对较少。乔金丽等[13]针对渗流作用影响下的隧道开挖面,采用有限差分法研究了其稳定性,并将计算结果与不考虑渗流作用的结果进行了对比,发现渗流作用对隧道开挖面的稳定性有很大的影响。王浩然等[14]基于弹塑性有限元法所得的渗流作用影响下开挖面的破坏模式,对现有的不考虑渗流作用的破坏模式进行了改进,并基于这一改进的破坏模式对开挖面的稳定性进行了极限分析。冯利坡等[15-16]基于水土压力统一计算理论和对数螺旋破坏模式,研究了水压力影响下的隧道开挖面的稳定性问题。ZHANG等[17]针对岩石介质中深埋隧道的开挖面,采用非线性Hoek-Brown强度准则,对其稳定性进行了非线性极限分析,并计算了开挖面的极限支护力。
有关孔隙水影响下开挖面的稳定性问题,现有文献只针对岩质隧道进行了讨论,而没有研究相应土体隧道的稳定性。鉴于此,本文针对均质土体中开挖的深埋盾构隧道,基于对数螺旋破坏机制,采用极限分析法推导了其开挖面支护力的计算公式。依据“穷举法”原理并编制数值优化程序,求得了特定参数下盾构隧道开挖面的极限支护力。此外,本文还通过参数分析讨论了土体重度γ、黏聚力c0、内摩擦角φ、水位高度H、开挖直径D和孔隙水压力系数ru对盾构隧道极限支护力的影响,所得结论可为地下水影响下盾构隧道的设计与施工提供指导。
1 极限分析法与强度准则极限分析法是研究岩土工程结构稳定性的有效方法,其不考虑材料复杂的弹塑性变形过程,而直接求解结构物在极限状态下的荷载以及相应速度场的分布。与极限平衡法、数值分析法等传统分析方法相比,极限分析法具有求解过程简单、结果意义明确等优点。根据Viratjandr和Michalowski[18]的研究,极限分析中孔隙水压力的影响可视为一外力作用于土体骨架上,其使土体发生体应变的功率和在边界上做的功率等价于孔隙水压力被视为内力时渗透力和浮力做的功率。考虑孔隙水压力影响的上限定理表达式为:
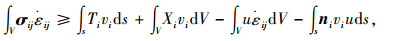
|
(1) |
式中,σij和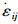
对于理想的弹塑性材料,其应力状态达到屈服强度后便发生塑性流动,即应力保持不变而应变无限增大。而实际工程中不容许结构物发生较大的变形,因此可认为此时已经发生破坏。在岩土工程领域,Mohr-Coulomb强度准则被广泛应用于土体材料屈服状态的判断,其不仅能准确地反映土体的真实破坏情况,而且具有适用范围大的优点。Mohr-Coulomb强度准则可用下式表示:
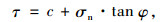
|
(2) |
式中,τ为土体的抗剪强度;σn为土体的正应力;c为土体的黏聚力;φ为土体的内摩擦角。
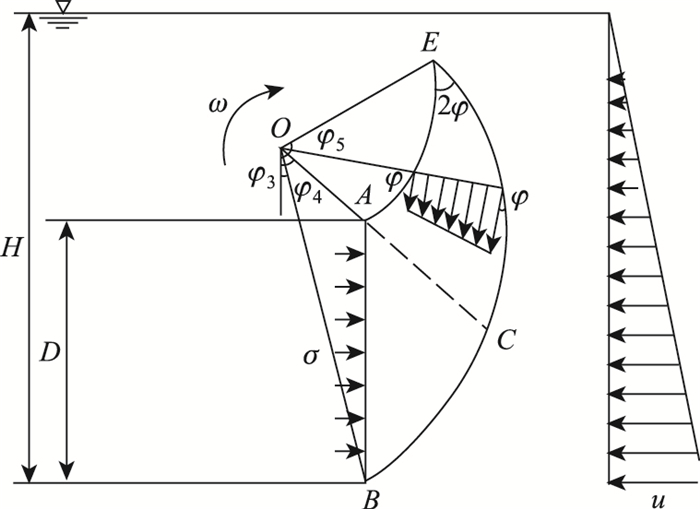
2 破坏机制的建立盾构隧道开挖面的破坏形式可分为主动破坏和被动破坏:当对开挖面施加的支护力较小时,由于支护力不足,发生主动破坏;当支护力较大时则发生被动破坏。对于浅埋盾构隧道,上覆土层相对较薄,这两种破坏形式都有可能发生。而深埋盾构隧道,开挖面的破坏形式主要表现为主动破坏。当开挖面前方土体发生破坏时,其滑动面应满足相关联流动法则,即要求滑动面的切线与相对速度方向的夹角等于土体的内摩擦角。研究表明,满足相关联流动法则的滑动面应为对数螺旋线。鉴于此,本文针对均质土体中开挖的深埋盾构隧道,建立了如图 1所示的开挖面主动破坏的对数螺旋破坏机制。其中,AB表示直径为D的盾构隧道开挖面,AE和BE为两条对数螺旋线,其旋转中心都在O点,分别由A点和B点开始生成,相交于E点,在E点的夹角为2φ。对于深埋隧道,交点E总是位于地表以下。
|
| 图 1 对数螺旋破坏机制及孔隙水压力分布 Fig. 1 Log spiral failure mechanism and pore water pressure distribution |
| |
令土体的内摩擦角为φ,则可得到AE和BE的方程如下:
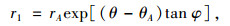
|
(3) |
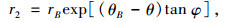
|
(4) |
式中,rA和rB分别表示OA及OB的长度;θA和θB分别为OA, OB与竖直方向的夹角。由对数螺旋线所定义的开挖面前方滑动体ABE以角速度ω顺时针绕旋转中心O转动。在盾构隧道掘进过程中,为了保证开挖面的稳定,需在开挖面上施加可近似于均匀分布的支护荷载σt。用θE表示OE与竖直方向的夹角,根据破坏机制的几何关系,可得到如下关系式:
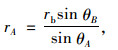
|
(5) |
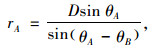
|
(6) |
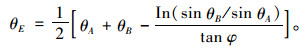
|
(7) |
由以上各式可发现,rA, rB及θE皆为θA和θB的函数。
3 极限分析过程 3.1 土体重力功率的计算为方便重力功率的计算,延长OA并与对数螺旋线BE相交于C点,如图 1所示,将破坏机制分为ABC和ACE两部分。对于区域ABC内土体的做功功率,可通过BOC和BOA两部分进行叠加得到,每一区域内重力功率如下:
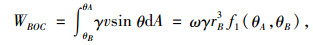
|
(8) |
式中,f1(θA, θB)的表达式为:
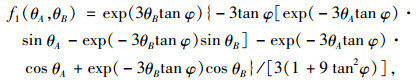
|
(9) |
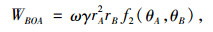
|
(10) |
式中,f2(θA, θB)的表达式为:
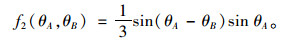
|
(11) |
同理,对于区域ACE内土体的做功功率,可由AOE和COE两部分叠加得到,每一区域内的功率如下:
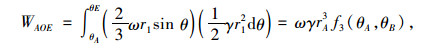
|
(12) |
式中,f3(θA, θB)的表达式为:
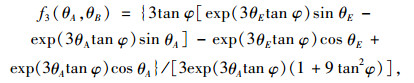
|
(13) |
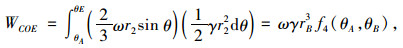
|
(14) |
式中,f4(θA, θB)的表达式为:
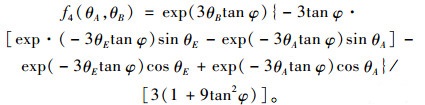
|
(15) |
综上可得总的重力功率如下:
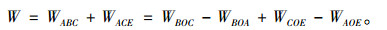
|
(16) |
将开挖面上施加的支护力视为均匀分布,可计算得支护力的功率为:
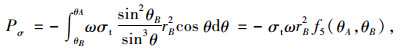
|
(17) |
式中,f5(θA, θB)的表达式为:
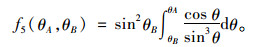
|
(18) |
由于极限分析中假定破坏体为刚体,则在极限状态时破坏体的体积保持不变,因而等式(1) 中右边第三项等于0,孔隙水压力的做功仅发生在速度间断面上:
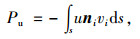
|
(19) |
式中,u为孔隙水压力。根据Michalowski[19]的研究成果,孔隙水压力可用下式进行简化计算:
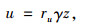
|
(20) |
式中,ru为孔隙水压力系数;z为土体到地下水位线的垂直距离。将孔隙水压力的功率沿破坏面进行积分,即可得到孔隙水压力总的做功功率。对于速度间断线AE,如图 1所示的几何关系,其上每一点到地下水位线的垂直距离为:
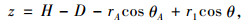
|
(21) |
式中,H为地下水位线到隧道底面的垂直距离,如图 1所示;D为隧道洞径;θ为对数螺旋线上一点与竖直方向的夹角。从而,计算得速度间断面AE上的孔隙水压力功率为:
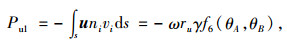
|
(22) |
式中,f6(θA, θB)的表达式为:
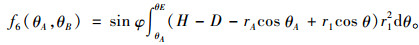
|
(23) |
同理,对于速度间断线BE,其上每一点到地下水位线的距离为:
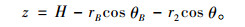
|
(24) |
计算得速度间断面BE上的孔隙水压力功率为:
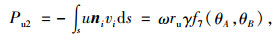
|
(25) |
式中,f7(θA, θB)的表达式为:
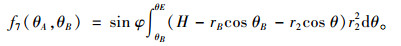
|
(26) |
由于刚体ABE的体积应变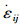
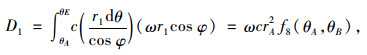
|
(27) |
式中,f8(θA, θB)的表达式为:
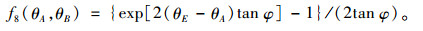
|
(28) |
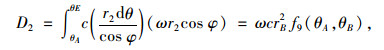
|
(29) |
式中,f9(θA, θB)的表达式为:
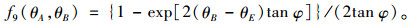
|
(30) |
根据极限分析的虚功率原理,联立以上各式,得到支护力的解析解如下:
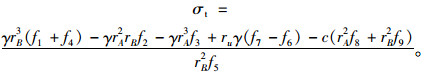
|
(31) |
此外,等式(29) 中的参数还应满足如下约束条件:
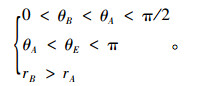
|
(32) |
为了保证盾构隧道开挖面的稳定,应计算开挖面所需的最小支护荷载,即破坏荷载的最大值。从式(31) 中可以发现,支护力σt是θA和θB的函数,因此,该问题可以转换为求式(31) 在约束条件(32) 下的数学优化问题。通过穷举法并进行编程,即可得到确定参数下支护力的上限解。
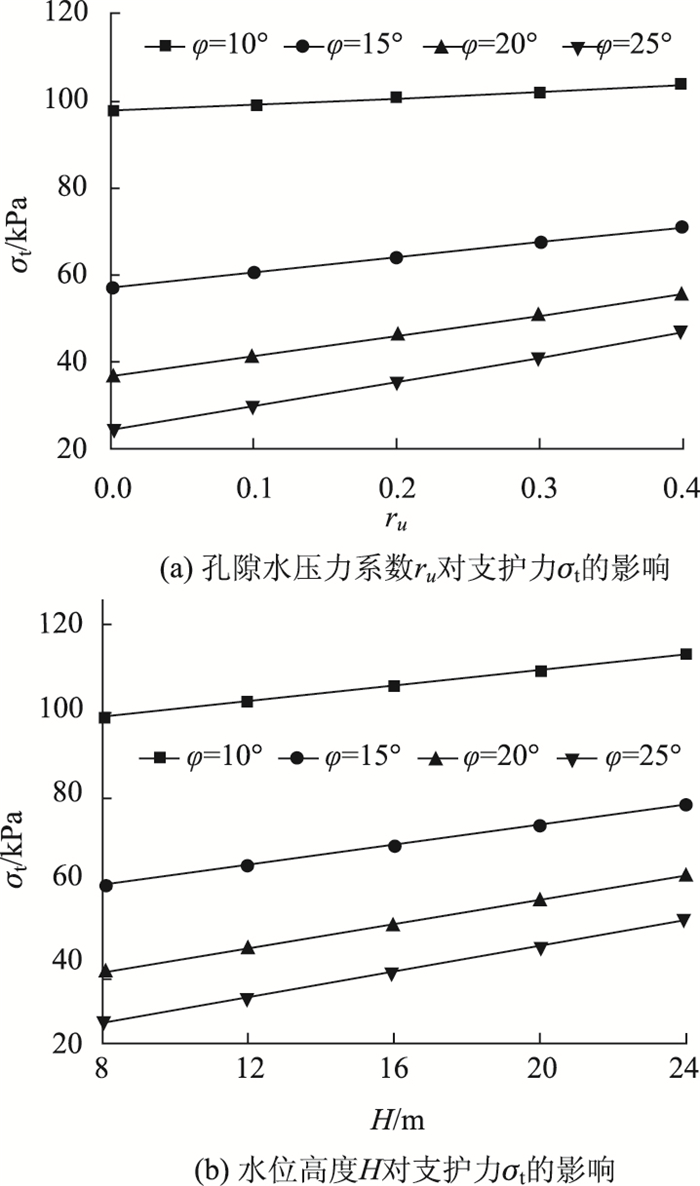
4 计算结果与分析 4.1 孔隙水压力对盾构隧道开挖面稳定性的影响为了研究孔隙水压力对盾构隧道开挖面稳定性的影响,依据现有文献中的数据[15-16],拟定各参数的取值如下:开挖直径D=8 m,土体重度γ=20 kN/m3,土体黏聚力c=10 kPa,土体内摩擦角φ=10°~25°。取地下水位高度H=8 m,得到不同孔隙水压力系数对开挖面极限支护力的影响,如图 2(a)所示,取孔隙水压力系数ru=0.1,得到不同地下水位高度对开挖面极限支护力的影响,如图 2(b)所示。此外,计算得到破坏机制随孔隙水压力系数ru及地下水位高度H的变化规律如图 3所示。
|
| 图 2 孔隙水压力对支护力的影响 Fig. 2 Influence of pore water pressure on supporting force |
| |
|
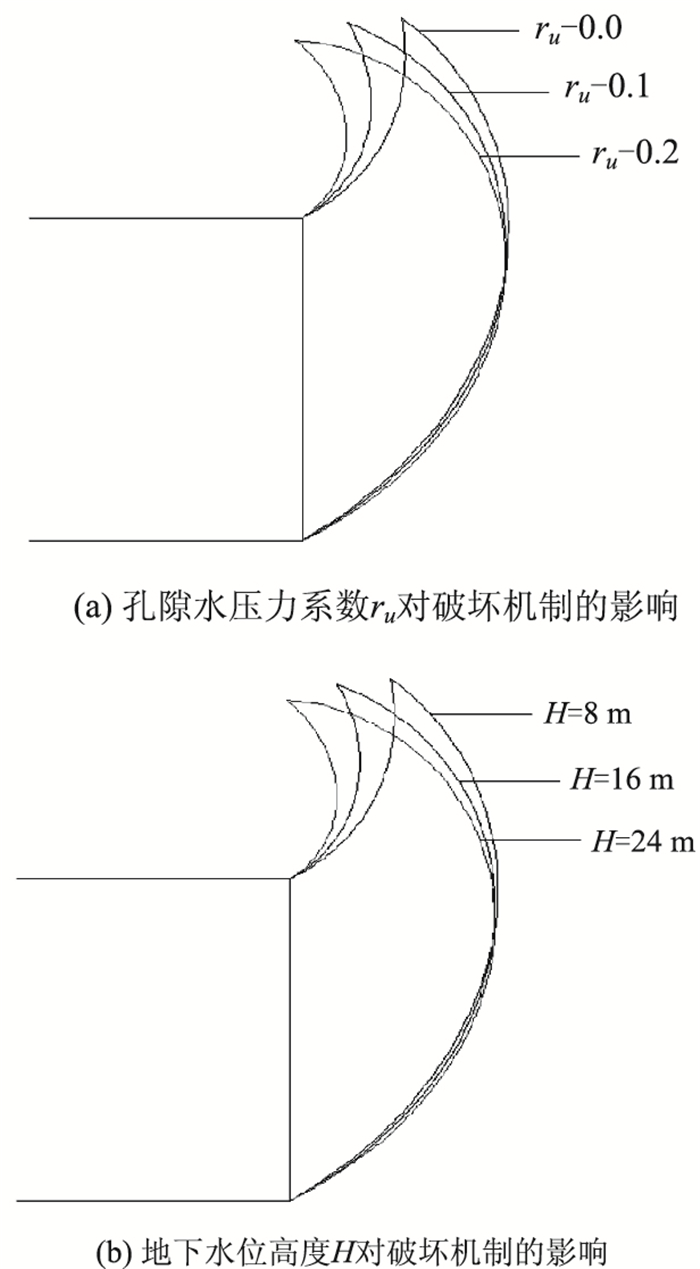
| 图 3 孔隙水压力对破坏机制的影响 Fig. 3 Influence of pore water pressure on failure mechanism |
| |
从图 2(a)中可以看出,极限支护力σt随着孔隙水压力系数ru的增大而增大,且当土体内摩擦角φ增大时,其变化幅度将变大。从图 2(b)中可以看出,极限支护力σt随着地下水位高度H的增大而增大,而内摩擦角φ的增加则对其变化幅度没有影响。此外,由图 2还可发现,极限支护力σt随着土体内摩擦角φ的增大而增大,且摩擦角增大时其变化幅度将增大。观察图 3可以发现,孔隙水压力系数的增大以及地下水位高度的增加对开挖面破坏机制的影响是一致的,都将导致破坏范围的增大。这种一致性是由于孔隙水压力系数的增大和地下水位高度的增加都导致了孔隙水压力做功的增大。而为了保持极限状态下的平衡,破坏面上的能量耗散也应随之增加,从而导致了破坏范围的增大。综合以上分析,建议在盾构隧道的设计与施工过程中应特别注意孔隙水对掌子面稳定性的影响,以保证工程建设的顺利完成。
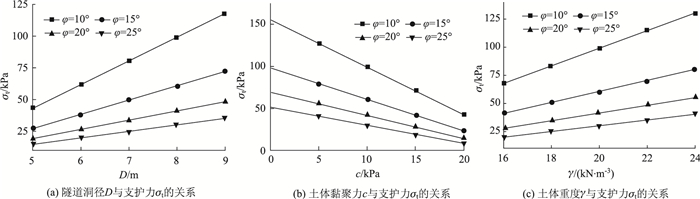
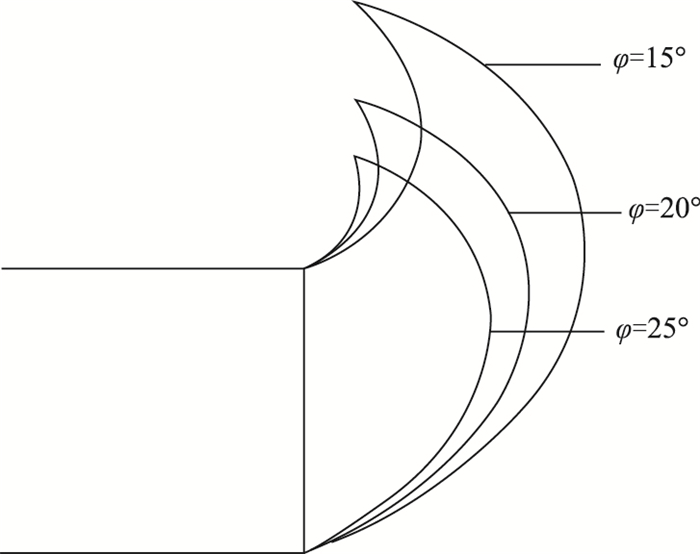
4.2 其他参数对盾构隧道开挖面稳定性的影响为了研究孔隙水压力影响下其他各参数对盾构隧道开挖面稳定性的影响,依据现有文献中的数据[15-16],拟定各参数的取值如下:孔隙水压力系数ru=0.1,地下水位高度H=8 m,土体内摩擦角φ=10°~25°。当土体黏聚力c=10 kPa和土体重度γ=20 kN/m3时,极限支护力随隧道洞径的变化如图 4(a)所示;当隧道洞径D=8 m和土体重度γ=20 kN/m3时,极限支护力随土体黏聚力的变化如图 4(b)所示;而当土体黏聚力c=10 kPa和土体洞径D=8 m时,极限支护力随土体重度的变化如图 4(c)所示。计算过程中还发现,土体重度对破坏机制的影响较小,而隧道洞径、土体黏聚力和内摩擦角对破坏机制的影响较大。其中,当隧道洞径D=8 m,地下水位高度H=16 m,孔隙水压力系数ru=0.1,土体重度γ=20 kN/m3,土体黏聚力c=12 kPa时,得到破坏机制随内摩擦角φ的变化规律如图 5所示。
|
| 图 4 其他参数对支护力的影响 Fig. 4 Influence of other parameters on supporting force |
| |
|
| 图 5 内摩擦角φ对破坏机制的影响 Fig. 5 Influence of internal frictional angle φ on failure mechanism |
| |
从图 4中可以看出,在考虑孔隙水压力的影响下,支护力σt随着隧道洞径D和土体重度γ的增大而增大,随着土体黏聚力c和内摩擦角φ的增大而减小。此外,从图 4中还不难发现,当土体内摩擦角较小时,极限支护力的变化幅度将增大。观察图 5可以发现,内摩擦角对破坏机制有较大的影响,破坏范围将随内摩擦角的变化而产生很大的变化。这种改变是由于破坏机制是基于关联流动法则构建的,滑动面的切线与相对速度方向的夹角等于土体的内摩擦角。因此,当内摩擦角变化时,对数螺旋破坏面将产生较大的改变。综合以上分析,建议在实际工程中,应根据现场的工程地质情况,进行有关隧道结构的设计,以保证隧道在建设及运营期间的安全可靠。
5 结论针对富水地区隧道施工开挖面稳定性问题,基于对数螺旋破坏机制与线性Mohr-Coulomb强度准则,提出了一种可考虑孔隙水压影响的开挖面支护力计算方法。该方法将孔隙水压视为作用在土体骨架上的外力,引入上限法的能耗计算中,并由此推导出相应的支护力表达式,其优势在于能快速获得富水风险地区稳定隧道开挖面所需的支护力和潜在破坏范围,为风险区段的隧道设计与施工提供指导。
| [1] | SAADA Z, MAGHOUS S, GAMIER D. Pseudo-static Analysis of Tunnel Face Stability Using the Generalized Hoek-Brown Strength Criterion[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(18): 3194-3212 |
| [2] | 郑永来, 冯利坡, 邓树新, 等. 高水压条件下盾构隧道开挖面稳定极限上限法研究[J]. 同济大学学报:自然科学版, 2013, 41(8): 1179-1184 ZHENG Yong-lai, FENG Li-po, DENG Shu-xin, et al. Study on Upper Bound Limit Method of Face Stability of Shield Tunnel with High-water Pressure[J]. Journal of Tongji University:Natural Science Edition, 2013, 41(8): 1179-1184 |
| [3] | 吕玺琳, 李冯缔, 黄茂松, 等. 三维盾构隧道开挖面极限支护压力数值及理论解[J]. 同济大学学报:自然科学版, 2012, 40(10): 1469-1473 LV Xi-lin, LI Feng-di, HUANG Mao-song, et al. Three-dimensional Numerical and Analytical Solutions of Limit Support Pressure at Shield Tunnel Face[J]. Journal of Tongji University:Natural Science Edition, 2012, 40(10): 1469-1473 |
| [4] | 赵炼恒, 孙秋红, 黄阜, 等. 非关联流动准则对浅埋隧道稳定性影响的上限分析[J]. 公路交通科技, 2012, 29(12): 101-106 ZHAO Lian-heng, SUN Qiu-hong, HUANG Fu, et al. Influences of Non-associated Flow Rule on Shallow Tunnel Stability Based on Upper Bound Limit Analysis[J]. Journal of Highway and Transportation Research and Development, 2012, 29(12): 101-106 |
| [5] | DAVIS E H, GUNN M J, MAIR R J, et al. The Stability of Shallow Tunnels and Underground Openings in Cohesive Material[J]. Géotechnique, 1980, 30(4): 397-416 |
| [6] | CHAMBON P, CORTE J F. Shallow Tunnels in Cohesionless Soil:Stability of Tunnel Face[J]. Journal of the Geotechnical Engineering, 1994, 120(7): 1148-1165 |
| [7] | LECA E, DORMIEUX L. Upper and Lower Bound Solutions for the Face Stability of Shallow Circular Tunnels in Frictional Materials[J]. Geotechnique, 1990, 40(4): 581-606 |
| [8] | SOUBRA A H. Three-dimensional Face Stability Analysis of Shallow Circular Tunnels[C]//International Conference on Geotechnical and Geological Engineering. Melbourne, Australia:ICGGE, 2000:19-24. |
| [9] | MOLLON G, PHOON K K, DIAS D, et al. Validation of a New 2D Failure Mechanism for the Stability Analysis of a Pressurized Tunnel Face in a Spatially Varying Sand[J]. Journal of Engineering Mechanics, 2010, 137(1): 8-21 |
| [10] | MOLLON G, DIAS D, SOUBRA A H. Rotational Failure Mechanisms for the Face Stability Analysis of Tunnels Driven by a Pressurized Shield[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(12): 1363-1388 |
| [11] | MOLLON G, DIAS D, SOUBRA A H. Range of the Safe Retaining Pressures of a Pressurized Tunnel Face by a Probabilistic Approach[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(11): 1954-1967 |
| [12] | SUBRIN D, WONG H. Tunnel Face Stability in Frictional Material:A New 3D Failure Mechanism[J]. Comptes Rendus Mecanique, 2002, 330(7): 513-519 |
| [13] | 乔金丽, 张义同, 许春彦. 考虑渗流的盾构隧道开挖面稳定性分析[J]. 水文地质工程地质, 2009(1): 80-85 QIAO Jin-li, ZHANG Yi-tong, XU Chun-yan. Stability Analysis of Shield TUNNEL Excavation Face with the Consideration of Seepage[J]. Hydrogeology and Engineering Geology, 2009(1): 80-85 |
| [14] | 王浩然, 黄茂松, 吕玺琳, 等. 考虑渗流影响的盾构隧道开挖面稳定上限分析[J]. 岩土工程学报, 2013, 35(9): 1696-1704 WANG Hao-ran, HUANG Mao-song, LV Xi-lin, et al. Upper Bound Limit Analysis of Stability of Shield Tunnel Face Considering Seepage[J]. Chinese Journal of Geotechnical and Engineering, 2013, 35(9): 1696-1704 |
| [15] | 冯利坡, 郑永来, 李文峋, 等. 盾构隧道开挖面对数螺旋破坏模式研究[J]. 华中科技大学学报:自然科学版, 2013, 41(6): 103-107 FENG Li-po, ZHENG Yong-lai, LI Wen-xun, et al. Log-spiral Failure Mechanisms of the Face Stability of Shield Tunnels[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2013, 41(6): 103-107 |
| [16] | 冯利坡, 郑永来, 邓树新, 等. 深埋盾构隧道开挖面三维对数螺旋破坏模式的上限分析[J]. 岩土力学, 2015, 36(7): 2105-2110 FENG Li-po, ZHENG Yong-lai, DENG Shu-xin, et al. Upper Bound Limit Analysis of Three-dimensional Log-spiral Failure Mode of Deep Shield Tunnel Face[J]. Rock and Soil Mechanics, 2015, 36(7): 2105-2110 |
| [17] | ZHANG Jia-hua, LI Yong-xin, XU Jing-shu. Energy Analysis of Face Stability of Deep Rock Tunnels Using Nonlinear Hoek-Brown Failure Criterion[J]. Journal of Central South University, 2015, 22(8): 3079-3086 |
| [18] | VIRATJANDR C, MICHALOWSKI R L. Limit Analysis of Submerged Slopes Subjected to Water Drawdown[J]. Canadian Geotechnical Journal, 2006, 43(8): 802-814 |
| [19] | MICHALOWSKI R L. Slope Stability Analysis:A Kinematical Approach[J]. Geotechnique, 1995, 45(2): 283-293 |
 2017, Vol. 34
2017, Vol. 34
