扩展功能
文章信息
- 袁鑫, 郑伟, Kumar DabnathSOJIB, 孙敏
- YUAN Xin, ZHENG Wei, Kumar Dabnath SOJIB, SUN Min
- 施工高温作用后CFRP板增强箱梁桥顶板界面有限元分析
- Finite Element Analysis on Interface of Top Plate of Box Girder Bridge Reinforced by CFRP Plate after Construction under High Temperature
- 公路交通科技, 2017, 34(7): 44-52
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(7): 44-52
- 10.3969/j.issn.1002-0268.2017.06.007
-
文章历史
- 收稿日期: 2016-10-20
2. 东南大学 土木工程学院, 江苏 南京 210096;
3. 苏州中固建筑科技有限公司, 江苏 苏州 215100;
4. 达卡工程技术大学 土木工程学院, 孟加拉 达卡 1212
2. School of Civil Engineering, Southeast University, Nanjing Jinagsu 210096, China;
3. Suzhou Zhonggu Architecture Technology Co., Ltd., Suzhou Jiangsu 215000 China;
4. School of Civil Engineering, Dhaka University of Engineering and Technology, Dhaka 1212, Bangladesh
近些年来,在土木工程加固领域,随着加固方面新材料的出现,自然对加固理论与加固技术也提出更新更高的要求,其中在加固新材料中,碳纤维增强聚合物(carbon fiber reinforced polymer, CFRP)用于土木工程结构加固是一项十分有优势的加固材料。与以往传统加固材料相比,CFRP具有轻质高强、较好的耐久性、耐腐蚀性等诸多优点,这些优点逐渐引起土木工程界日益关注[1-3]。另外CFRP板还具有施工快捷方便、高弹性模量的优点,越来越多的成功加固案例出现在土木结构加固特别是桥梁加固当中。
在CFRP加固理论和分析研究中,对于CFRP板加固剥离数值模拟分析问题,借助精细单元进行有限元分析方法计算量比较大,不便于在大规模土木工程和科研中应用,同时考虑到非线性分析能力有限,基于无网格法组合裂缝模型的分析不方便不适合广泛使用,所以迄今为止这两种有限元分析方法还未能实现大规模的应用。
前人通过无网格法分析,利用精细单元模型获得的结果,为后人选用普通单元模型分析提供了一定经验,这使得受弯剥离方面的数值分析问题有可能趋于简化分析。迄今为止,这些界面单元有限元分析模型大部分是对在常规加固环境中本构模型进行模拟和应用,然而这些模型并未考虑施工中可能有些特殊情况的存在会带来什么影响。目前在CFRP-混凝土的界面有限单元模型选取和建立方面,国内外学者是通过有限元数值分析及结合试验分析而获得的[4-9]。然而, 特殊环境下比如沥青摊铺后高温环境下,针对FRP-混凝土界面有限单元模型的研究基本没有。考虑到FRP-混凝土界面有限单元模型是钢筋混凝土结构有限元分析和建立强度模型的基础, 因此, 非常有必要进行此方面的相关研究。
文中研究背景是在孟加拉国Bangabandhu大桥CFRP板加固该桥箱梁桥顶板时,在大桥顶板横向粘贴碳纤维板来约束纵向裂缝发展,同时对大桥桥面铺设5 cm厚的沥青玛蹄脂耐磨层,该施工高温环境起因是CFRP板加固后需要重新摊铺沥青玛蹄脂桥面铺装层,所以数值模拟分析的对象和以往不同,该研究对象是经过沥青摊铺施工高温作用后的CFRP板加固的箱梁桥顶板。文中借助通用有限元程序,基于普通单元的模型,单元尺寸大小划分适中。
为了研究铺设沥青玛蹄脂时高温作用下新的CFRP板-混凝土本构模型及有限元受弯剥离分析问题,文中嵌入CFRP板-混凝土之间的界面单元模型及黏结-滑移双重剥离破坏准则,使得混凝土单元受弯剥离分析可以借助界面单元来实现,通过有限元程序调用CFRP板-混凝土界面单元。界面应力和剥离破坏的研究对象都是基于高温作用后的界面应力和剥离破坏,并不是考虑沥青摊铺瞬时的高温作用,而是重在研究高温作用后稳定的界面剥离及破坏现象。所开展数值模拟分析采用CFRP板材性参数和界面黏结-滑移关系都是建立在高温作用基础上得出的,并将有限元分析结果和试验结果进行对比研究分析。
1 自定义界面单元引入陆新征建议的双重剥离破坏准则来自定义FRP板-混凝土界面单元[10-11],有限元数值模拟考虑沥青摊铺施工高温作用。双重剥离破坏准则简单介绍如下:
(1) 无裂缝剥离准则-滑移场比较均匀,界面的整体单向滑动引起剥离破坏,定义为黏结-滑移模型Ⅰ,当界面单元节点的滑移量大于黏结强度最大时刻对应的滑移量时,界面产生剥离。其适用范围:受弯裂缝距离FRP板-混凝土界面比较远,混凝土单元并未开裂。
(2) 裂缝剥离准则-在界面单元内部,局部滑移集中,即存在并非均匀变化的滑移场,定义为黏结-滑移模型Ⅱ,此时定义裂缝两侧界面滑移量为等值,因为裂缝的宽度等于裂缝两侧界面的总滑移量,裂缝两侧发生剥离破坏的明显特征是混凝土裂缝宽度大于两倍黏结强度最大时刻对应的滑移量数值。其适用范围:界面单元内部的滑移场存在滑移集中而非均匀变化,与界面单元相连的混凝土单元有裂缝产生。
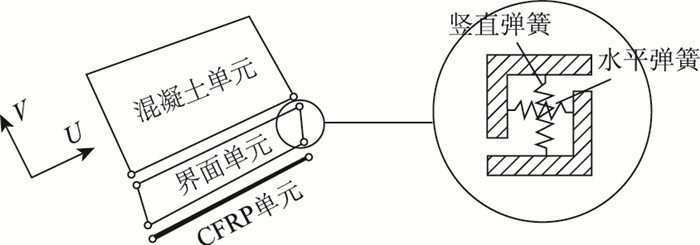
受弯剥离的CFRP板-混凝土界面单元考虑界面黏结滑移与剥离破坏准则。借助4个节点的两组弹簧单元描述CFRP板-混凝土界面单元,借助竖向弹簧Kv和水平弹簧Ku连接混凝土和CFRP板单元。CFRP板-混凝土界面的非线性可以通过弹簧单元来描述,U为水平方向;V为竖直方向;如图 1所示。竖直弹簧Kv没有剥离破坏时Kv刚度无穷大,剥离破坏时Kv=0[12]。这样可以利用双重剥离准则准确估计裂缝附近由滑移集中导致的剥离破坏。
|
| 图 1 界面单元形状 Fig. 1 Interface unit shape |
| |
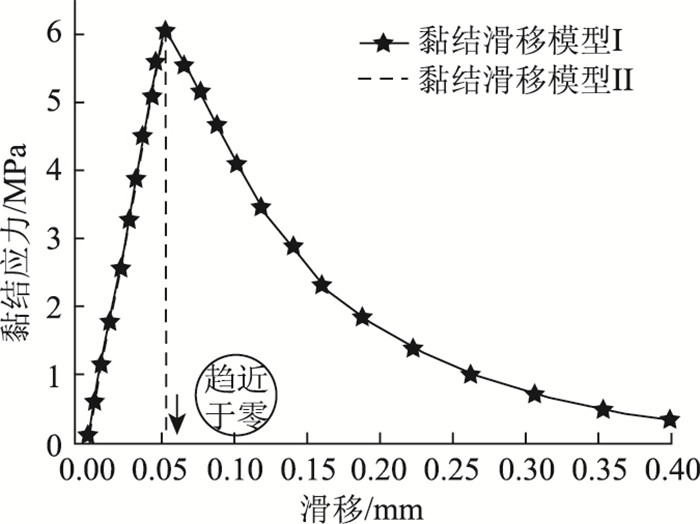
界面应力峰值τmax与混凝土表面抗拉强度相关,但由于黏结胶层向混凝土层的渗透产生的化学胶结力、黏结胶与混凝土层的机械咬合力和摩擦力的作用,这都增强了界面的黏结能力。由于纤维材料粘贴宽度比混凝土构件宽度小时,应力通过纤维板传递到混凝土时会引起混凝土构件范围内应力的不均匀分布,黏结区域外的混凝土所起的作用使得界面破坏达到较高的剪应力,图 2引入文献[13]建议的公式, 并依据文献[14]给出的试验数值和黏结滑移模型得出。
|
| 图 2 界面黏结-滑移关系 Fig. 2 Interface bonding-slip relationship |
| |
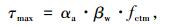
|
(1) |
式中,αa为黏结增强系数;βw为宽度比系数;fctm为混凝土的表面抗拉强度。
依据文献[14]界面应力峰值τmax取平均值6 MPa,拟合得到的黏结增强系数αa为1.688。滑移值s0与纤维片材的力学性能、黏结胶层和混凝土的力学性能、黏结胶与混凝土渗透结合层的力学性能等因素相关,据此可以给出图 2黏结-滑移关系。
黏结-滑移模型Ⅰ:
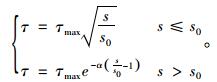
|
(2) |
黏结-滑移模型Ⅱ:
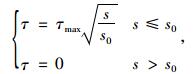
|
(3) |
式中,s0为初始滑移量; τmax为最大滑移量对应的最大剪力。黏结-滑移模型Ⅰ适用范围:与界面单元相连的混凝土单元没有开裂,界面距离受弯裂缝比较远;黏结-滑移模型Ⅱ适用范围:界面单元内部的滑移场存在滑移集中而非均匀变化,与界面单元相连的混凝土单元中存在裂缝。
2 有限元模型和材料本构模型借助MSC.MARC,混凝土单元通过Element 3四节点平面应力单元描述,混凝土单元的尺寸为15~50 mm的普通尺寸;钢筋单元用Element 143描述;CFRP板单元用平面桁架单元Element 9描述,如图 3所示。用MSC.MARC中自带的弹塑性混凝土模型定义混凝土的本构关系。根据箍筋配置量不同来描述开裂后混凝土的受剪行为。对配一定量箍筋的混凝土梁,开裂后混凝土的裂面剪力传递系数取为β=0.8(β值可依据试验具体情况调整)。

|
| 图 3 有限元单元材料类型 Fig. 3 Finite element unit material types |
| |
通过非线性有限元软件MARC的USELEM子程序调用,引入双重剥离破坏准则,并考虑沥青摊铺施工高温作用。
用户自定义界面单元USELEM子程序调用:subroutine uselem
(m, xk, xm, nnode, ndeg, f, r, jtype, dispt, disp, ndi, nshear, ipass0, nstats, ngenel, intel, coord, ncrd, iflag, idss, t, dt, etota, gsigs, de, geom, jgeom, sigxx, nstrmu)。
(1) 刚度矩阵和高斯积分数值积分
文中混凝土和钢筋的模拟采用四节点平面单元,下面以平面四节点等参元为例来说明有限元计算中刚度矩阵的形成过程。用相同的形状函数和同样的节点,单元的几何坐标与位移的单元采用插值的方式表示。
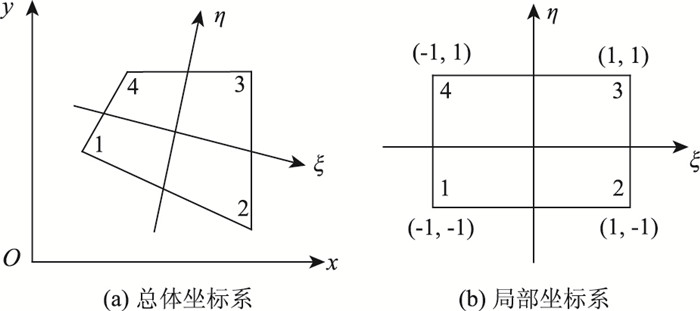
在分析中出现两套坐标系:被分析物体的实际单元采用总体坐标系xOy;另一套采用标准化的正方形单元的局部坐标系ξOη,在等参元分析中也称母单元,在边界上有ξ=±1和η=±1,在母单元上建立位移插值函数是容易的,可以通过图像变换中的映射方法实现,如图 4所示。
|
| 图 4 坐标映射 Fig. 4 Coordinate mapping |
| |
实际单元中任一点坐标与节点坐标有如下关系,即:
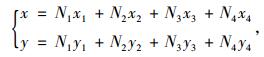
|
(4) |
式中,xi,yi(i=1, 2, 3, 4) 是节点坐标。
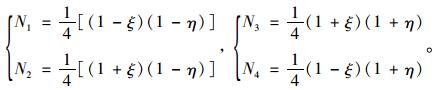
|
(5) |
Ni为(ξ,η)的形函数,通过这样的变换,母单元上每一点(ξ,η)可以在实际单元中找到其对应点(x,y),两单元间形成一一对应关系,而且4个角点与4边界上也形成一一对应关系,母单元中建立插值函数如下:
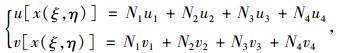
|
(6) |
式中,ui,vi(i=1, 2, 3, 4) 为节点位移,Ni(i=1, 2, 3, 4) 为形函数,与坐标变换中的形函数相同,有了位移分布函数就可以求得单元内各点的应变为:
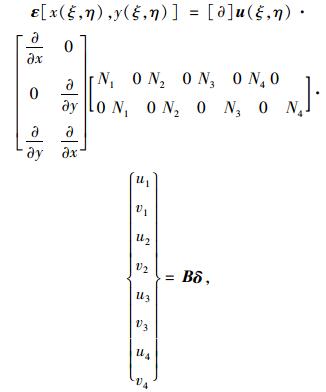
|
(7) |
式中,B为几何矩阵,在几何矩阵中用形函数对整体坐标x,y微分,形函数是用局部坐标ξ,η表示,这时需要进行坐标变换,利用复合函数求导公式,即:
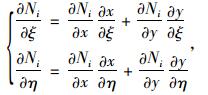
|
(8) |
用矩阵形式表示,即:
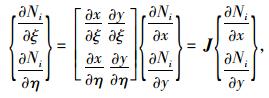
|
(9) |
其中,
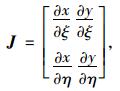
|
(10) |
称为雅克比矩阵,求逆后得
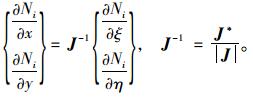
|
(11) |
Ni(ξ,η)对ξ, η的求导是容易的,代入式(10) 可求得[J],进而利用J-1求得Ni,x,y的偏导数。于是:
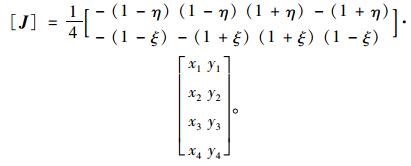
|
(12) |
这样就求出几何矩阵,再利用公式
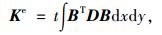
|
(13) |
式中,Ke为单元刚度;B为几何矩阵;D为对角矩阵。
四节点等参元的单元刚度公式变换为:
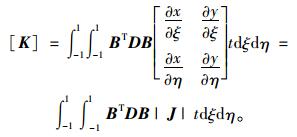
|
(14) |
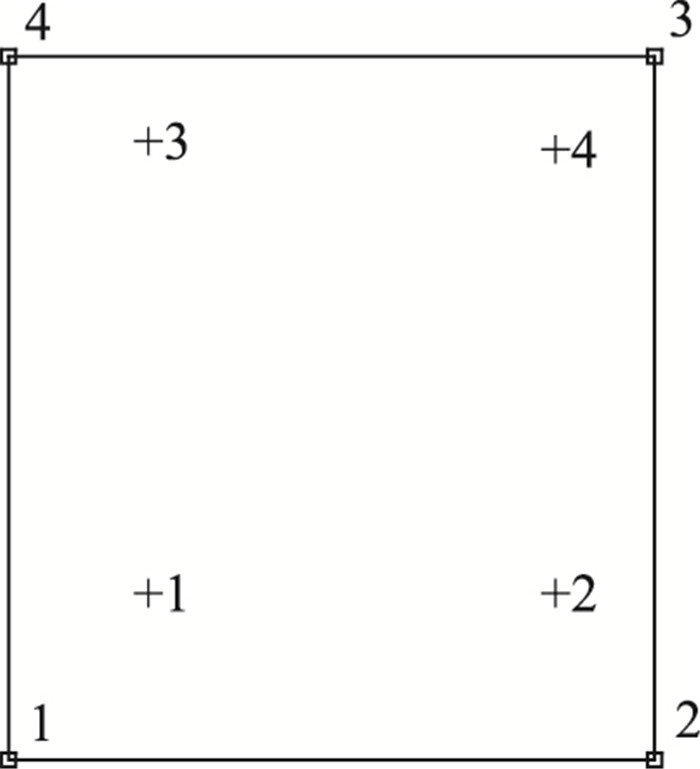
这些计算均可在母单元内进行,考虑到几何矩阵的复杂性,一般很难通过直接积分求出结果,在有限元分析中可以通过高斯数值积分法求解。高斯数值积分法是优化选择积分点和积分权函数,n个插值结点非等距分布高斯积分点如图 5所示,积分权系数如表 1所示。
|
| 图 5 高斯积分点 Fig. 5 Gauss integral points |
| |
| 积分点n | 高斯积分点 | 高斯积分权因子 |
| 1 | 0.0 | 2.0 |
| 2 | ±0.577 350 3 | 1.0 |
| 0.0 | ||
| 3 | ±0.774 596 7 | ±0.555 556 |
| 0.0 | ±0.888 889 | |
| 4 | ±0.861 136 3 | ±0.347 854 8 |
| ±0.339 981 0 | ±0.652 145 2 |
一个函数的定积分可以通过n个节点的函数值加权组合来表示,通过图 5和表 1的高斯积分点和积分权系数,高斯积分n个插值结点非等距分布的积分计算公式为:
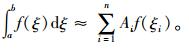
|
(15) |
采用预先定义积分点和相应的加权系数的高斯积分方法,被积分的函数在指定积分点上的数值先被求得,然后利用加权后求和方法得到该函数的积分。众所周知采用n个积分点的高斯积分,可以达到2n-1阶的精度,如果被积分的函数是2n-1次多项式,则通过n个积分点的高斯积分可以得到精确的积分结果,该方法具有最高的计算精度。平面四节点等参元高斯求积公式一般形式为:
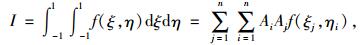
|
(16) |
式中, Ai, Aj为权因子; f(ξ)为函数ξ的局部坐标函数;f(ξj, ηi)为函数ξ, η的局部坐标函数。
3 材料本构模型(1) 混凝土本构选用
采用MSC.MARC[15]中的弹塑性混凝土模型、Buyukozutrk[16]建议的屈服面模型,由式(17) 给出:
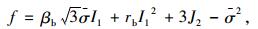
|
(17) |
式中,I1为第一应力不变量;J2为第二偏应力不变量;f为屈服面;βb和rb为修正系数;σ为等效应力;根据Buyukozuturk的建议:βb选用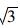
该模型采用增量弹塑性本构关系及关联流动法则,混凝土单轴受压应力-塑性应变曲线由用户定义,硬化法则的计算可以通过利用式(18)、(19) 的转换关系获得等效应力-等效塑性应变关系曲线来实现。
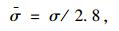
|
(18) |
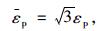
|
(19) |
式中,σ为等效应力; εp为等效塑性应变。
通过增量弹塑性本构理论,屈服后硬化方程可表示为:
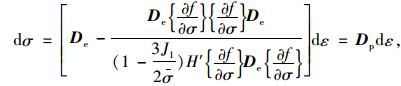
|
(20) |
式中,De为材料弹性本构矩阵;参数H′为硬化参数;Dp为屈服后硬化的材料弹性本构矩阵,按式(21) 计算:
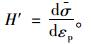
|
(21) |
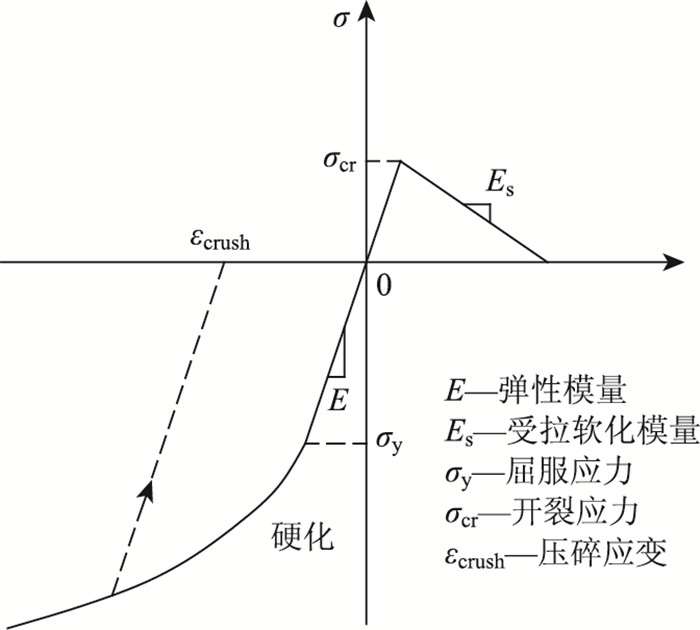
混凝土本构模型的主要参数如图 6所示。对于普通混凝土,混凝土的单轴受压试验可以看出,当混凝土受压应力达到(0.3~0.4)fc之前,受压的应力应变关系为直线形式,变形表现为弹性变形,这个时候混凝土材料的屈服应力可采用图 6中应力峰值强度的1/3。
|
| 图 6 混凝土本构模型参数图 Fig. 6 Concrete constitutive model parameter diagram |
| |
当混凝土被压碎,材料完全退出工作时,混凝土的压应变相应达到极限应变峰值。可以借助开裂应力和软化模量来描述混凝土的开裂和受拉线性软化特征。混凝土的裂面受剪行为可通过恒值的裂面剪力传递系数来描述。根据文献[17]的建议,普通钢筋混凝土梁的剪力系数为0.5,钢筋混凝土深梁为0.25,剪切行为明显的剪力墙剪力系数为0.125。
(2) 钢筋本构选用
由于钢筋和混凝土单元之间共用节点,可采用理想弹塑性模型(虽然钢筋滑移对构件刚度有一定程度影响,但其对构件剥离承载力影响并不大),以简化计算分析。
(3) CFRP板本构模型
CFRP板可采用断裂材料模型和线弹性模型来描述,一旦CFRP板应力达到断裂应力, 随即表现为断裂,应力骤然为零。
4 现场沥青摊铺施工高温作用模拟(1) 由于实际受加固的箱梁梁顶板在粘贴CFRP板条后现场摊铺高温沥青,为了准确模拟施工高温和车载作用,具体施工顺序介绍如下。
对CFRP增强混凝土板进行养护,养护期间对CFRP板条进行均匀加压养护,养护3~7 d,养护期间不得施加外力影响。采用水泥浆和丙烯酸乳胶漆进行表面涂装养防护,高温沥青铺装后采用重型机械对沥青碾压, 使得CFRP板条增强混凝土板铺装表面平整,如图 7和图 8所示。

|
| 图 7 现场高温沥青摊铺 Fig. 7 In-situ high-temperature asphalt paving |
| |

|
| 图 8 现场高温沥青碾压 Fig. 8 In-situ high-temperature asphalt rolling process |
| |
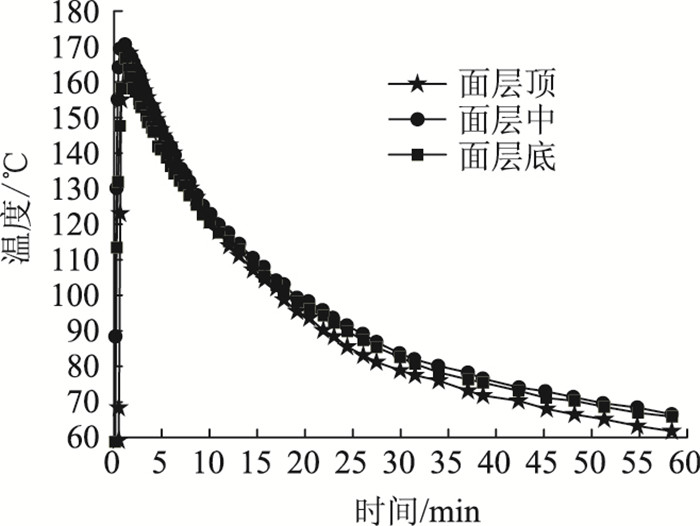
由图 9可以看出沥青面层最高温度达到172 ℃,经历60 min后面层顶部恢复到62 ℃,面层中部恢复到68 ℃,面层底部恢复到67 ℃。
|
| 图 9 沥青面层不同位置温度随时间变化 Fig. 9 Asphalt surface temperature at different locations vary with time |
| |
(2) 在碳纤维板上侧和下侧中间部位分别埋设热电偶探头,测试沥青摊铺过程中碳纤维板上、下侧的温度变化情况。热电偶探头现场埋设如图 10所示。温度测试精度为0.1 ℃,温度测试结果如图 11所示。

|
| 图 10 CFRP板温度测试热电偶探头埋设图 Fig. 10 Burying thermocouple detector for temperature test of CFRP plate |
| |
|
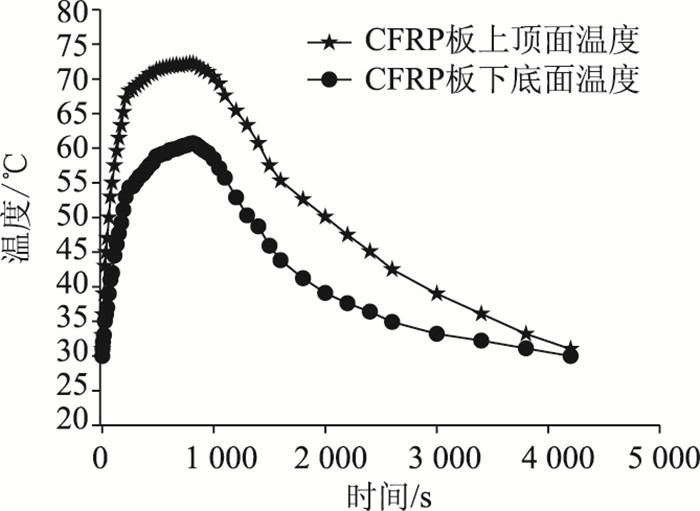
| 图 11 CFRP板温度随时间变化曲线 Fig. 11 CFRP plate temperature varying with time |
| |
由图 11可以看出CFRP板上侧和下侧温度,在上升段温度曲线变化趋势陡峭,温度下降段温度曲线变化趋势平缓,CFRP板上下侧最高温度分别是72.2 ℃和60.7 ℃。
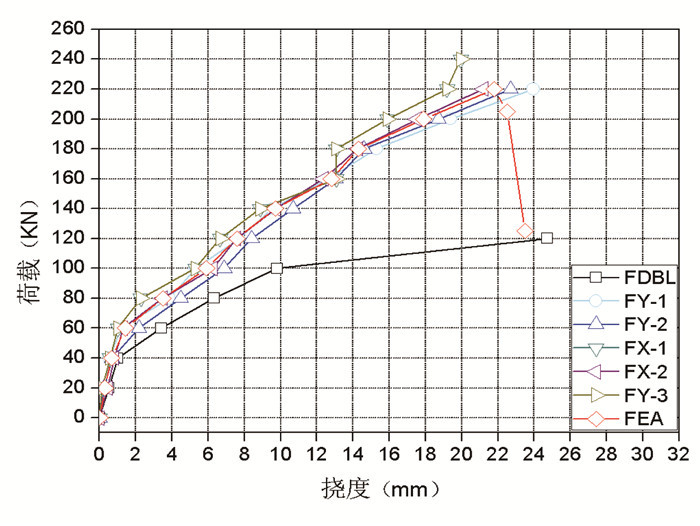
5 有限元和试验结果对比分析借助界面单元的引入,有限元模型可以用普通单元来描述分析,通过位移控制加载,可以得到整个荷载挠度全曲线。图 12~图 13中FDBL为未经过CFRP板加固的对比梁,FEA为经过CFRP板加固并经过沥青摊铺施工高温作用的有限元分析试验梁,其他均为经过CFRP板加固并经过沥青摊铺施工高温作用的试验梁,试验梁尺寸和加载情况具体见文献[18]。有限元计算结果和试验结果对比讨论如下。
|
| 图 12 A组试件试验和有限元结果比较 Fig. 12 Comparing of finite element analysis and test results of group A specimen |
| |
|
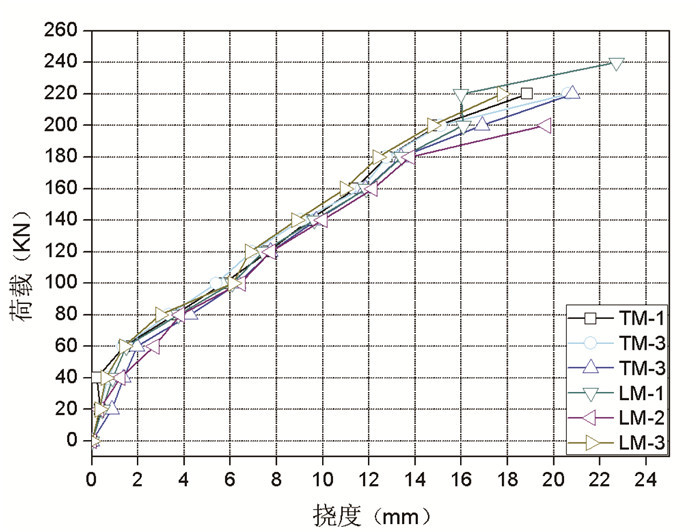
| 图 13 B组锚固试件荷载挠度曲线图 Fig. 13 Load-deflection curves of group B anchored specimens |
| |
5.1 荷载挠度曲线
荷载-挠度曲线试验值和有限元值对比见图 12,可以看出考虑双剥离破坏准则的普通有限元模型预测的剥离起始点与试验基本吻合,裂缝附近出现滑移集中现象引起了剥离破坏,可以较好估计剥离承载力。当外加荷载较小时,试件处于弹性阶段,FDBL与A,B组试件的荷载挠度曲线基本重合。当纯弯段出现第一条裂缝后,拉力由钢筋承担,FDBL由于受拉区混凝土退出工作。A,B组试件在受拉区混凝土退出工作后,拉力由CFRP板条与钢筋共同承担,CFRP板条的引入延缓截面中和轴上升速度。
钢筋混凝土试件粘贴了CFRP板条后,一方面CFRP板条分担了钢筋的拉力,另一方面,由于CFRP板条与混凝土界面之间的黏结剪应力的存在,裂缝回缩减小从而减小了裂缝的宽度提高了试件的刚度,使得试件不会立即破坏。从图 13可以看出,当荷载加载到180 kN(屈服荷载前一级)后采用附加横向压条的锚固措施后结构刚度退化,其刚度值略小于没有附加锚固措施的试件刚度。
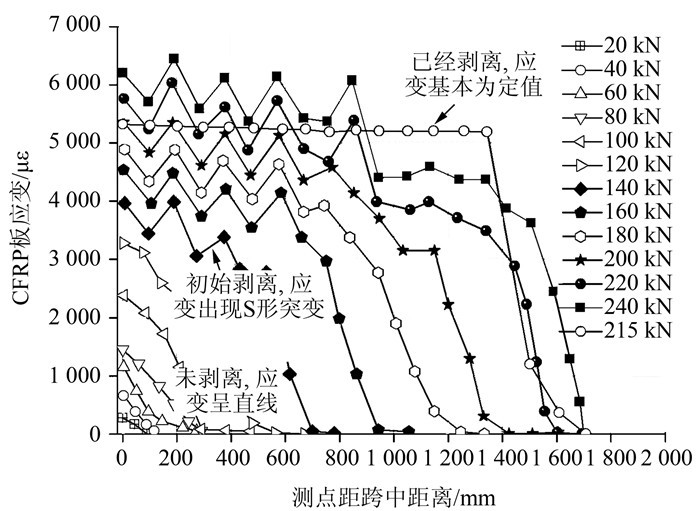
5.2 CFRP板应变CFRP板应变发展如图 14所示,与试验所测得的CFRP板应变分布规律基本吻合。可以看出,当荷载小于120 kN时,CFRP板-混凝土界面并未产生裂缝,说明CFRP板-混凝土间黏结性能尚好。沿着跨中向梁端方向,CFRP板应变值递减。当荷载加载140 kN之后,在试验梁跨中附近的CFRP板-混凝土界面层,出现初始剥离,在界面层剥离区域,曲线斜率下降幅度明显,CFRP板应变曲线形态近似呈S形。剥离区界面的摩擦剪力促使CFRP板上的应变值逐渐增大,这时界面滑移主要表现为裂缝张开引起的局部滑移。随着剥离区长度不断增大,S形应变分布朝自由端发展,最后,在剥离(P=240 kN)发生前,裂缝张开导致的滑移成为界面应力的主要组成部分。剥离破坏一旦发生,荷载值随之骤然下降,在剥离区,CFRP板的应变值恒定不变,如图 14所示。
|
| 图 14 CFRP板应变图 Fig. 14 Strain diagram of CFRP plate |
| |
5.3 裂缝开展
由图 15可以看出,裂缝开展有限元模拟与实际试件的裂缝开展很相似,说明通过引入双重剥离破坏准则可以较好估计裂缝附近由滑移集中导致的剥离。裂缝开展试验结果与有限元数值分析结果吻合较好。通过有限元数值模拟分析得到剥离图来看,剥离首先从加载截面附近的裂缝处开始剥离,即纯弯区和弯剪区交界面,这也与试验观察结果一致。文中的单元有限元模型可以较为准确地模拟IC debonding破坏。

|
| 图 15 裂缝逐级开展图 Fig. 15 Figures of crack gradually propagation |
| |
有限元计算得到的平均剥离承载力(如果只根据界面单元节点的相对滑移量来判断剥离与否而不采用虑双重剥离破坏准则)要比试验结果大30%左右。普通尺寸单元无法正确模拟裂缝附近的滑移集中现场(未采用“裂缝剥离准则”),其计算结果将会较高估剥离承载力。综上所述,普通单元有限元模型如何正确模拟IC debonding的关键,取决于是否采用双重剥离破坏准则。
6 结论文中对SMA摊铺的高温作用后的界面有限单元进行定义和回归分析,并借助界面有限单元对CFRP板箱梁桥顶板进行有限元研究,可以得出如下结论:
(1) 通过用户自定义界面单元,引入双重剥离破坏准则,对CFRP板进行剥离破坏分析。考虑双剥离破坏准则的普通有限元模型预测的剥离起始点与试验观测结果基本一致。
(2) 在受弯剥离的CFRP板-混凝土界面单元中考虑界面黏结滑移与剥离破坏准则。借助4个节点的两组弹簧单元描述CFRP板-混凝土界面单元,CFRP板-混凝土界面的非线性可以通过弹簧单位来描述。
(3) 根据箍筋配置不同来描述开裂后混凝土受剪,混凝土的开裂形态借助开裂应力描述,受拉软化形态借助软化模量描述,较好地模拟了特殊环境下的CFRP板-混凝剥离破坏。
(4) 混凝土单元和钢筋单元之间共用节点,不考虑二者之间的滑移而采用理想弹塑性模型。CFRP板采用断裂材料模型和线弹性模型,一旦CFRP板应力达到断裂应力,随即发生断裂,此时应力骤然为零。
(5) 当荷载阶段相对较小,CFRP板-混凝土界面并未出现裂缝,CFRP板与混凝土间黏结性能尚好,随着荷载增加,在试验梁跨中附近的CFRP板-混凝土界面层,出现初始剥离现象。随着荷载的增加,在剥离区长度范围内,S形应变逐渐增大沿自由端方向扩展,初始剥离一旦开始,荷载随之骤然下降,在剥离区域,CFRP板的应变维持恒值不变。
| [1] | MOHAMED H M, MASMOUDI R. Flexural Strength and Behavior of Steel and FRP-reinforced Concrete-filled FRP Tube Beams[J]. Engineering Structures, 2010, 32(11): 3789-3800 |
| [2] | SEBASTIAN W, ZHANG C. Observations from Testing of Indeterminate FRP-plated Steel Beams on Flexible Supports[J]. Composites Part B:Engineering, 2013, 45(1): 200-214 |
| [3] | CHEN J F, YUAN H, TENG J G. Debonding Failure Along a Softening FRP-to-concrete Interface Between Two Adjacent Cracks in Concrete Members[J]. Engineering Structures, 2007, 29(2): 259-270 |
| [4] | TANAKA T. Shear Resisting Mechanism of Reinforced Concrete Beams with CFS as Shear Reinforcement[D]. Hokkaido, Japan:Hokkaido University, 1996. http://cn.bing.com/academic/profile?id=0485f87296a6f6992b5fee883b61e7cf&encoded=0&v=paper_preview&mkt=zh-cn |
| [5] | MAEDA T, ASANO Y. A Study on Bond Mechanism of Carbon Fiber Sheet[C]//Proceedings of the Third Symposium on Non-metallic(FRP)Reinforcement for Concrete Structures. Sapporo, Japan:CRC Press, 1997:279-285. http://www.academia.edu/12963449/IR_thermography_for_interface_analysis_of_FRP_laminates_externally_bonded_to_RC_beams |
| [6] | TALJSTEN B. Strengthening of Existing Concrete Structure with Epoxy Bonded Plates of Steel of Fiber Reinforced Plastics[D]. Lulea, Sweden:Lulea University of Technology, 1994. http://www.mendeley.com/research/plate-bonding-strengthening-existing-concrete-structures-epoxy-bonded-plates-steel-fibre-reinforced/ |
| [7] | 郭诗惠, 张建仁, 高勇, 等. 胶层厚度对CFRP板材与混凝土界面黏结性能影响[J]. 公路交通科技, 2015, 32(9): 87-97 GUO Shi-hui, ZHANG Jian-ren, GAO Yong, et al. Effect of Adhesive Thickness on Bond Behavior of CFRP Plate-concrete Interface[J]. Journal of Highway and Transportation Research and Development, 2015, 32(9): 87-97 |
| [8] | GEMERT D V. Force Transfer in Epoxy-bonded Steel-concrete Joints[J]. International Journal of Adhesion and Adhesives, 1980, 1(2): 67-72 |
| [9] | KHALIFA A, GOLD W J, NANNI A, et al. Contribution of Externally Bonded FRP to Shear Capacity of RC Flexural Members[J]. Journal of Composite and Construction, 1998, 2(4): 195-202 |
| [10] | 陆新征, 谭壮, 叶列平, 等. FRP布-混凝土界面黏结性能的有限元分析[J]. 工程力学, 2004, 21(6): 45-50 LU Xin-zheng, TAN Zhuang, YIE Lie-ping, et al. Finite Element Analysis of Debonding at the Interface Between Frp Sheet and Concrete[J]. Engineering Mechanics, 2004, 21(6): 45-50 |
| [11] | 陆新征, 叶列平, 滕锦光, 等. FRP-混凝土界面黏结滑移本构模型[J]. 建筑结构学报, 2005, 26(4): 10-18 LU Xin-zheng, YE Lie-ping, TENG Jin-guang, et al. Bond-slip Model for FRP-to-concrete Interface[J]. Journal of Building Structures, 2005, 26(4): 10-18 |
| [12] | 陆新征. FRP-混凝土界面行为研究[D]. 北京: 清华大学, 2004. LU Xin-zheng. Studies on FRP-concrete Interface[D]. Beijing:Tsinghua University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10003-2005148150.htm |
| [13] | CHEN J F, TENG J G. Anchorage Strength Models for FRP and Steel Plates Bonded to Concrete[J]. Journal of Structural Engineering, 2001, 127(7): 784-791 |
| [14] | 袁鑫. 施工高温与车载多场作用下CFRP板增强桥梁试验与理论研究[D]. 南京: 东南大学, 2014. YUAN Xin. Experiment and Theoretical Research on CFRP Plat Reinforced Bridges under Action of Construction at High Temperature and Vehicle Load[D].Nanjing:Southeast University, 2014. http://d.g.wanfangdata.com.cn/Thesis_Y2758454.aspx |
| [15] | ÖCHSNERM. The Finite Element Analysis Program MSC.MARC/Mentat[M]. Singapore: Springer Singapore, 2016. |
| [16] | BUYUKOZTURK O. Nonlinear Analysis of Reinforced Concrete Structures[J]. Computers and Structures, 1977, 7(1): 149-156 |
| [17] | 江见鲸, 陆新征, 叶列平. 混凝土结构有限元分析[M]. 北京: 清华大学出版社, 2005. JIANG Jian-jing, LU Xin-zheng, YE Lie-ping. Finite Element Analysis of Concrete Structures[M]. Beijing: Tsinghua University Press, 2005. |
| [18] | 袁鑫, 张继文, 胡江贝. CFRP板加固箱梁桥顶板在沥青施工高温作用后剥离破坏分析[J]. 中国公路学报, 2014, 27(3): 71-79 YUAN Xin, ZHANG Ji-wen, HU Jiang-bei. Debonding Failure Analysis of CFRP Reinforced Box Girder Bridge Top Slab Subjected to High Temperature During Asphalt Pavement Construction[J]. China Journal of Highway and Transport, 2014, 27(3): 71-79 |
 2017, Vol. 34
2017, Vol. 34
