扩展功能
文章信息
- 朱云升, 杨柳, 王开凤, 包云晗
- ZHU Yun-sheng, YANG Liu, WANG Kai-feng, BAO Yun-han
- 用分形几何理论评价旧路面沥青混合料级配变异性
- Evaluation of Gradation Variation of Asphalt Mixture in Old Pavement with Fractal Geometry Theory
- 公路交通科技, 2017, 34(7): 14-19
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(7): 14-19
- 10.3969/j.issn.1002-0268.2017.07.003
-
文章历史
- 收稿日期: 2016-08-15
2. 中国市政工程中南设计研究总院有限公司, 湖北 武汉 430063
2. Central and Southern China Municipal Engineering Design & Research Institute Co., Ltd, Wuhan Hubei 430063, China
近年来,我国高速公路建设发展迅速,沥青路面已成为当今道路的主流类型。影响沥青路面路用性能的因素众多,其中矿料级配的类型和组成对其使用性能及力学特性起到了十分重要的影响,其级配的变异性更是其中非常重要的一点。在沥青混合料级配的理论研究中,有两种常用的理论:最大密度曲线理论和粒子干涉理论[1],这两种理论是传统上研究集料级配的理论基础,目前,级配的变异性一般用变异系数μi来表示,公式如下[2]:
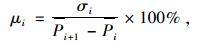
|
(1) |
式中, μi为第i级变异系数;σi为第i级分计筛余百分率标准差;Pi+1为第i+1级平均累计筛余百分率;Pi为第i级平均累计筛余百分率。
从上面的公式可以看出,目前级配的变异性一般是用来描述同一个样本内的级配差异情况,如μ4.36很大,则说明了4.36 mm筛孔各个样本的分计筛余通过率相差大,这档集料的级配变异大。但笔者认为这种变异性的表达有不全之处,在沥青道路施工中,生产配合比的确定是要经过理论计算和试验验算,是最合适的级配,施工时的实际级配与生产配合比之间的差距和变异更需要我们去关注研究[3]。
分形理论是近代随着材料科学的发展而发展起来的一种新理论,它主要研究自然界中不规则、无序的事物[4],将分形理论应用在道路工程方面的研究还处于初步发展阶段,分形中的分维值D可以和沥青混合料的级配、压实性及抗车辙能力等建立相关联系[1],但是应用于级配变异性方面的研究很少。文中主要是利用分形几何理论去研究上述的级配变异性,提出控制级配变异性的技术参数。
1 分形几何理论简介自然界中大部分事物都是不规则的、无序的,是传统的欧氏几何无法描述的,分形理论的出现让大家可以从新的角度去研究、去认识这些不规则的事物和现象。分形是由美籍数学家B Mandelbrot首先提出的。1967年他在美国权威杂志《Science》上发表了题为《英国的海岸线有多长?统计自相似和分数维度》的著名论文,首次提出了分形的概念,使学术界认识到了自然界中分形的存在[4]。1975年,他创立了分形几何学,在此基础上,形成了研究分形性质及其应用的科学,称为分形理论。
目前,对于分形的判断常采用自相似分形的幂律定义[5]:
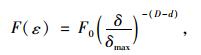
|
(2) |
式中,F(ε)为某一几何图形的长度、面积、或体积。F0为几何图形为整形(D=1) 时的长度、面积、或体积。δ为长度尺码。ε为无量纲尺码长度。D为分形维数。d为分形的拓扑维数,对于分形曲线,d=1;对于分形曲面,d=2;对于三维分形体,d=3。
在分形理论中有两个重要的原则:自相似原则和迭代生成原则。自相似性是分形理论中非常重要的特征,它表征了分形形体整体与局部之间的联系,它们之间的相似可以是完全相同的,仅在尺度上不同,也可以是统计意义上的相似,自然界中分形形体的相似性一般是后者。迭代生成原则是数学上研究分形的一种重要手段,如康托(Cantor)三分集、科契(Koch)雪花曲线、谢尔宾斯基(Sierpinski)地毯等,这些分形模型均是通过某种迭代方式形成的,通过这些模型去研究分形的性质。
分形理论是非线性科学的前沿和重要分支,是当今学界内非常热门的一种理论,它还有待于进一步完善和发展。
2 集料级配的分形推导集料是沥青混合料的主要构成部分,集料特征(集料形状、规格、级配)等决定了沥青混合料的体积构成,影响着混合料各方面的性能[6]。由于集料加工方式的多样性、压实过程中的变异性等因素的影响,导致压实后集料的几何形状、粒径分布、级配以及性能等呈现出一定的不规则性和复杂性,使得我们很难利用准确的数学公式去描述、去评价集料的这种不规则性、复杂性[7],但是集料的粒径大小及动力学机制是相同的,在统计意义上也表现出一定尺度范围内的自相似特征,如粒径、体积等,所以可以利用分形理论对其加以研究[8-10]。
集料的拓扑维数d=3,根据分形的幂律定义可以得到其毛体积的分形表达式:
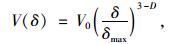
|
(3) |
式中,V(δ)为粒径不大于集料颗粒的毛体积;V0为所有集料的毛体积。
对式(3) 求导得:
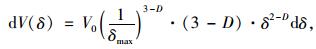
|
(4) |
式中dV(δ)为区间(δ,δ+dδ)内集料的体积。
定义粒径小于集料的质量M(δ),则有:
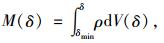
|
(5) |
由式(4)、(5) 得:
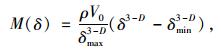
|
(6) |
式中,M(δ)为粒径不大于δ的集料质量;ρ为集料的表观密度。
当δ=δmax时:
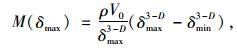
|
(7) |
定义集料的质量分布函数:
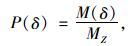
|
(8) |
式中,P(δ)为筛孔为δ的质量通过百分率;MZ为集料的总质量,即MZ=M(δmax)。
结合式(6)、(8) 可得:
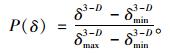
|
(9) |
实际工程中,集料的最小粒径一般很小,所以可以将δmin3-D忽略,即δmin3-D=0,可得到:
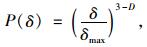
|
(10) |
此即为质量通过率表示的集料级配分形表达式。
集料级配分维数D的计算方法目前主要可以分为以下两种[11]:一是根据式(10) 中集料的各级筛孔通过率利用计算机迭代求出;二是利用lg(P)与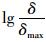
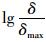
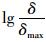
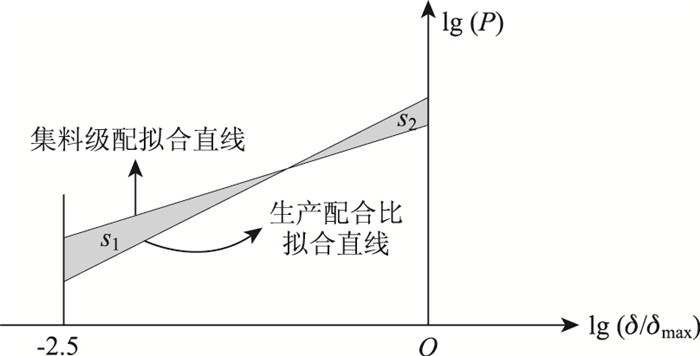
在文中,级配的变异性专指路面铺筑的集料级配与生产配合比产生的差异,这主要是由于集料的来源、集料加工方式、现场管理等各种因素造成的。这里可以利用分形理论对其进行计算描述,在双对数坐标中,可以得到集料级配的拟合直线与生产设计配合比拟合直线,在固定区间内两者所围成的面积可以描述两者的差异[12],即级配变异性,如图 1所示。
|
| 图 1 变异系数计算示意图 Fig. 1 Schematic diagram of calculating variable coefficient |
| |
面积越大,说明变异性越大;面积越小,说明变异性越小。公式如下:
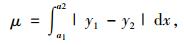
|
(11) |
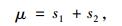
|
(12) |
式中,μ为变异系数;y1为集料级配拟合直线;y2为生产配合比拟合直线;a1,a2为固定区间;文中取[-2.5,0];s1,s2为两直线围成区域的面积。
3 集料级配的分形试验研究前文已经对集料级配的分形进行了推导,并给出了集料级配分维数D的计算方法。本节利用室内试验计算分析得到实际道路路面的级配数据[13],对这些级配数据进行分形处理,求出相应的分维数D,并求出规范中级配上下限的分维数,将几者进行比较,得出集料级配分维数D的一些性质[14-15],并计算出级配变异系数。
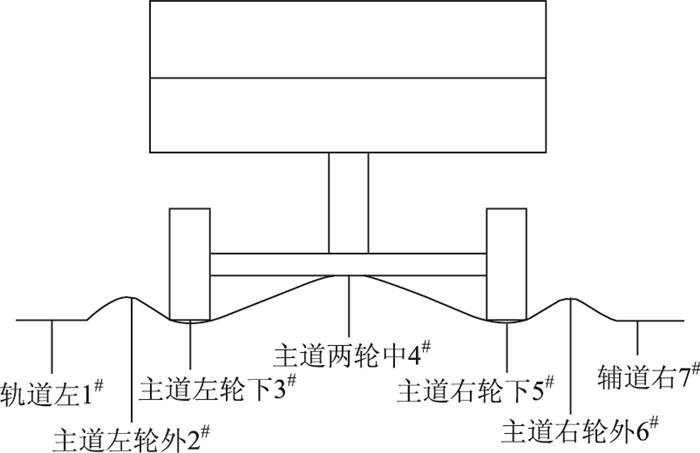
对黄石市某市政公路进行钻芯取样,如图 2所示,将所取芯样分成3组,即左右轮下,两轮中,两轮外,这样更有针对性地研究车辙路面的级配变异,用切割机对每组芯样进行切割,切成上中下3个面层,如图 3所示,按照规范[16]通过对沥青混合料燃烧后的矿质集料进行筛分试验,可以得到各组芯样分层的级配[17]。得到的级配信息见表 1。

|
| 图 2 取样示意图 Fig. 2 Schematic diagram of sampling |
| |
|
| 图 3 切割后的芯样 Fig. 3 Core samples after cutting |
| |
| 位置 | 不同粒径δ(mm)下的通过率P/% | ||||||||||||
| 31.5 | 26.5 | 19 | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
| 两轮外 上面层 | — | — | — | 100 | 98.20 | 89.56 | 63.07 | 35.85 | 19.51 | 12.53 | 5.98 | 4.46 | 4.03 |
| 两轮中 上面层 | — | — | — | 100 | 93.58 | 84.38 | 65.80 | 32.81 | 20.49 | 10.76 | 6.08 | 4.34 | 3.99 |
| 两轮下 上面层 | — | — | 100 | 92.46 | 83.23 | 68.47 | 46.39 | 26.43 | 18.90 | 12.31 | 10.30 | 6.79 | 4.35 |
| 生产配合比(上) | — | — | 100 | 100 | 99.60 | 72.60 | 44.00 | 28.30 | 21.20 | 15.20 | 9.60 | 7.80 | 6.40 |
| 两轮外 中面层 | — | 100 | 98.89 | 97.61 | 88.73 | 66.67 | 42.85 | 30.59 | 17.22 | 7.36 | 4.26 | 3.15 | 2.28 |
| 两轮中 中面层 | — | 100 | 98.33 | 94.89 | 85.33 | 70.22 | 47.67 | 30.11 | 15.33 | 7.00 | 4.22 | 3.11 | 2.67 |
| 两轮下 中面层 | — | 100 | 94.34 | 84.92 | 70.90 | 56.56 | 33.93 | 23.28 | 15.49 | 11.89 | 6.64 | 5.57 | 4.51 |
| 生产配合比(中) | — | 100 | 93.00 | 83.00 | 68.00 | 53.00 | 34.00 | 21.00 | 15.00 | 11.00 | 9.00 | 7.00 | 6.00 |
| 两轮外 下面层 | 100 | 99.27 | 95.77 | 88.78 | 79.01 | 61.97 | 32.89 | 17.26 | 11.59 | 7.18 | 4.09 | 3.41 | 2.27 |
| 两轮中 下面层 | 100 | 100 | 98.28 | 92.74 | 79.31 | 65.42 | 42.86 | 23.42 | 11.79 | 7.03 | 4.22 | 3.20 | 2.97 |
| 两轮下 下面层 | 100 | 97.84 | 80.84 | 71.53 | 62.21 | 50.84 | 30.89 | 18.47 | 14.63 | 10.79 | 7.37 | 5.26 | 4.16 |
| 生产配合比(下) | 100 | 94.10 | 75.70 | 68.00 | 59.80 | 51.50 | 35.00 | 21.30 | 14.30 | 9.40 | 7.30 | 5.80 | 4.50 |
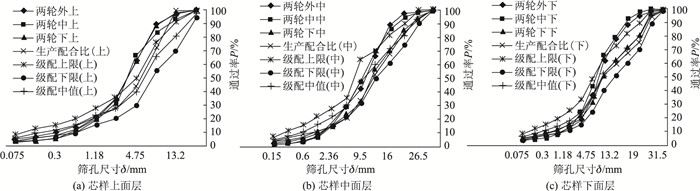
将得出的各组级配绘制成曲线,并在双对数坐标图中对其进行线性拟合,见图 4和图 5。
|
| 图 4 各组芯样级配曲线图 Fig. 4 Gradation curves of core samples |
| |
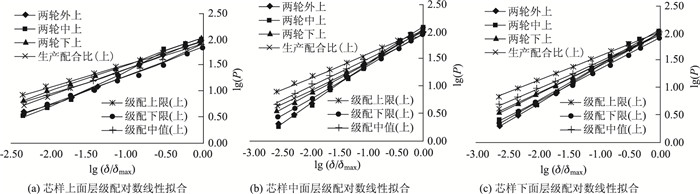
|
| 图 5 各组芯样级配对数线性拟合图 Fig. 5 Gradation logarithm linear fitting curves of core samples |
| |
由以上各图可以得到各组芯样级配的最佳拟合直线斜率K,可以计算出各组芯样级配的分维值D、相关系数R2以及变异系数μ,结果见表 2。
| 芯样编号 | 斜率K (3-D) |
分维值 D |
相关系数 R2 |
变异系数 μ |
| 两轮外 上面层 | 0.674 0 | 2.326 | 0.983 7 | 0.251 4 |
| 两轮中 上面层 | 0.673 6 | 2.326 4 | 0.982 4 | 0.264 7 |
| 两轮下 上面层 | 0.518 6 | 2.481 4 | 0.990 8 | 0.229 9 |
| 级配上限(上) | 0.452 9 | 2.547 1 | 0.982 8 | 0.277 8 |
| 级配下限(上) | 0.561 0 | 2.439 | 0.979 6 | 0.339 6 |
| 级配中值(上) | 0.494 9 | 2.505 1 | 0.988 | 0.068 0 |
| 生产配合比(上) | 0.537 7 | 2.462 3 | 0.985 5 | — |
| 两轮外 中面层 | 0.712 2 | 2.287 8 | 0.986 5 | 0.349 2 |
| 两轮中 中面层 | 0.704 9 | 2.295 1 | 0.982 6 | 0.336 7 |
| 两轮下 中面层 | 0.567 5 | 2.432 5 | 0.990 1 | 0.094 8 |
| 级配上限(中) | 0.447 7 | 2.552 3 | 0.989 6 | 0.429 1 |
| 级配下限(中) | 0.609 9 | 2.390 1 | 0.997 3 | 0.234 9 |
| 级配中值(中) | 0.507 4 | 2.492 6 | 0.997 4 | 0.163 8 |
| 生产配合比(中) | 0.515 8 | 2.484 2 | 0.975 6 | — |
| 两轮外 下面层 | 0.688 1 | 2.311 9 | 0.989 6 | 0.276 9 |
| 两轮中 下面层 | 0.677 4 | 2.322 6 | 0.982 3 | 0.232 0 |
| 两轮下 下面层 | 0.551 9 | 2.448 1 | 0.991 8 | 0.021 4 |
| 级配上限(下) | 0.448 7 | 2.551 3 | 0.998 3 | 0.413 2 |
| 级配下限(下) | 0.591 5 | 2.408 5 | 0.983 8 | 0.284 1 |
| 级配中值(下) | 0.501 7 | 2.498 3 | 0.995 8 | 0.131 3 |
| 生产配合比(下) | 0.539 8 | 2.460 2 | 0.991 9 | — |
分析上文的图表可以得到以下结果:
(1) 在级配线性拟合图中,各拟合直线的相关系数R2都比较大,接近1,说明数据的直线相关性都比较好,反映了试验得出的级配是基本符合分形理论的。
(2) 从表 2中可以看出级配的目标配合比(级配中值)的分维值在2.50左右,即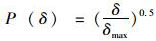
(3) 变异系数μ可以用来表示级配的变异情况,μ越大,变异越大; μ越小,变异越小; 从表 2中可以看出级配中值的μ比较小,因为生产配合比是以级配中值为目标进行设计的,级配中值变异性偏小是必然的;轮迹带外侧及两轮中芯样的变异系数相较于两轮下偏大,级配变异较大,这可能是轮迹带的集料在高温荷载的作用下产生横向剪切流动所致。
(4) 在规范[18]中对级配允许波动范围做出了规定,有3个指标,如下:粒径δ=0.075 mm(±2%)、δ≤2.36 mm(±5%)、δ≥4.75 mm(±6%),从表 1中可以看出两轮下的中下面层级配满足指标,其变异系数μ分别为0.094 8,0.021 4,可以提出适合本试验的指标:当μ≤0.1时,级配的变异性是在可允许范围内的。
4 结论(1) 试验中沥青混合料的级配比较符合分形理论的结果,利用分形理论研究级配是可行的。
(2) 分维值D是分形理论中的重要参数,在沥青混合料集料级配的研究中,分维值D一定程度上揭示了级配曲线形态的分布规律, 为研究描述沥青混合料的级配,提供了一种新角度。
(3) 级配的变异性可以用变异系数μ来进行量化,如利用μ值对拌和站生产的沥青混合料和生产配合比验证中试验段铺筑的级配进行评价,可以有效防止施工过程中级配变异偏大,对施工生产具有一定的指导意义。
(4) 级配变异是沥青混合料生产过程中不可避免的,一般施工过程中都需要确定级配允许的波动范围,利用变异系数μ可以对此进行进一步的量化,防止级配变异过大,文中提出了适合本次试验的范围指标,但不具备广泛性,要得出广泛性的结论需要以大量的试验数据为基础,还需要进行更深入的研究。
| [1] | 蒋双全, 张争奇, 杨博. 分形几何理论在沥青混合料研究中的应用[J]. 公路, 2009(10): 198-203 JIANG Shuang-quan, ZHANG Zheng-qi, YANG Bo. Application of Fractal Geometry Theory to Study on Asphalt Mixture[J]. Highway, 2009(10): 198-203 |
| [2] | 虞海珍, 李小青, 江滔. 高速公路沥青混合料级配和油石比变异性分析[J]. 中国市政工程, 2007(2): 12-14, 87 YU Hai-zheng, LI Xiao-qing, JIANG Tao. Analysis on Expressway Asphalt Mixture Gradation & Asphalt Content Variability[J]. China Municipal Engineering, 2007(2): 12-14, 87 |
| [3] | 董泽蛟, 肖桂清, 龚湘兵. 级配及抗车辙剂对沥青混合料抗车辙性能的影响分析[J]. 公路交通科技, 2014, 31(2): 27-31, 46 DONG Ze-jiao, XIAO Gui-qing, GONG Xiang-bing. Analysis on Impact of Gradation and Anti-rutting Additive on Rutting Resistance of Asphalt Mixture[J]. Journal of Highway and Transportation Research and Development, 2014, 31(2): 27-31, 46 |
| [4] | MANDELBROB B. How Long is the Coast of Britain? Statistical Self-similarity and Fractional Dimension[J]. Science, 1967, 156(3775): 636-638 |
| [5] | 高远. 沥青混合料集料级配优化与分形研究[D]. 衡阳: 南华大学, 2008. GAO Yuan. Study on Asphalt Mixture Aggregate Gradation Optimization and Fractal[D]. Hengyang:University of Nanhua, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10540-2009200976.htm |
| [6] | 高文阳, 王莉. 基于分形理论的大粒径沥青混合料评价方法研究[J]. 中外公路, 2012, 32(5): 244-248 GAO Wen-yang, WANG Li. Study on Evaluation Method of Large Size Asphalt Mixture Based on Fractal Theory[J]. Journal of China & Foreign Highway, 2012, 32(5): 244-248 |
| [7] | ARASAN S, AKBULUT S, HASILOGLU A S. The Relationship between the Fractal Dimension and Shape Properties of Particles[J]. KSCE Journal of Civil Engineering, 2011, 15(7): 1219-1225 |
| [8] | HOU Y, HUANG Y, SUN F, et al. Fractal Analysis on Asphalt Mixture Using a Two-dimensional Imaging Technique[J]. Advances in Materials Science and Engineering, 2016, 2016(2): 1-7 |
| [9] | WANG Hai-nian, BU Yin, WANG Yan-zhe, et al. The Effect of Morphological Characteristic of Coarse Aggregates Measured with Fractal Dimension on Asphalt Mixture's High-temperature Performance[J]. Advances in Materials Science & Engineering, 2016, 2016: 1-9 |
| [10] | 韩立志, 梁增洁, 彭余华, 等. AC-25级配离析的分形评价标准及预测方法[J]. 长安大学学报:自然科学版, 2014, 34(6): 27-33 HAN Li-zhi, LIANG Zeng-jie, PENG Yu-hua, et al. Fractal Evaluation Criteria and Prediction Method of AC-25 Gradation Segregation[J]. Journal of Chang'an University:Natural Science Edition, 2014, 34(6): 27-33 |
| [11] | 赵战利. 基于分形方法的沥青路面抗滑技术研究[D]. 西安: 长安大学, 2005. ZHAO Zhan-li. Study on Anti-slide Technology of Asphalt Pavement Based on Fractal Method[D]. Xi'an:Chang'an University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-11941-2006030552.htm |
| [12] | 赵艳纳. SMA-13施工过程中集料质量变异性研究[J]. 公路, 2015(9): 240-244 ZHAO Yan-na. Research of SMA-13 Aggregate Quality Variability during Its Construction Process[J]. Highway, 2015(9): 240-244 |
| [13] | 毛菊良, 杨群, 陈在林, 等. 沥青路面钻芯芯样级配差异性分析[J]. 公路交通科技, 2006, 23(5): 19-22 MAO Ju-liang, YANG Qun, CHEN Zai-lin, et al. Analysis of Gradation Difference of Core Sample from Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development, 2006, 23(5): 19-22 |
| [14] | 陈国明, 谭忆秋, 王哲人, 等. 沥青混合料级配曲线走向的分形研究[J]. 公路交通科技, 2005, 22(1): 1-4 CHEN Guo-ming, TAN Yi-qiu, WANG Zhe-ren, et al. Fractal Study of Grading Curve Trend of the Asphalt Mixtures[J]. Journal of Highway and Transportation Research and Development, 2005, 22(1): 1-4 |
| [15] | 陈龙, 何兆益, 陈宏斌. 基于分维度指标的泡沫沥青冷再生基层路用性能研究[J]. 公路交通科技, 2016, 33(2): 1-5 CHEN Long, HE Zhao-yi, CHEN Hong-bin. Research of Road Performance of Cold Recycled Pavement Base with Foamed Asphalt Based on Fractal Dimension[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2): 1-5 |
| [16] | JTG E20-2011, 公路工程沥青及沥青混合料试验规程[S]. JTG E20-2011, Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering[S]. |
| [17] | 吴莹, 马刚, 周伟, 等. 基于分形理论的堆石料级配优化研究[J]. 岩土力学, 2016, 37(7): 1977-1985 WU Ying, MA Gang, ZHOU Wei, et al. Optimization of Gradation of Rockfill Materials Based on the Fractal Theory[J]. Rock and Soil Mechanics, 2016, 37(7): 1977-1985 |
| [18] | JTG F40-2004, 公路沥青路面施工技术规范[S]. JTG F40-2004, Technical Specifications for Construction of Highway Asphalt Pavements[S]. |
 2017, Vol. 34
2017, Vol. 34
