扩展功能
文章信息
- 张宏, 张海龙, 王智远
- ZHANG Hong, ZHANG Hai-long, WANG Zhi-yuan
- 沙漠区沥青混凝土路面横向隆起现象的力学分析
- Mechanical Analysis of Asphalt Concrete Pavement Transverse Blowup in Desert Area
- 公路交通科技, 2017, 34(7): 8-13
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(7): 8-13
- 10.3969/j.issn.1002-0268.2017.07.002
-
文章历史
- 收稿日期: 2016-06-07
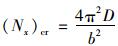 is more reasonable. After that, the expression of the flexural rigidity and the method of determining the position of the neutral axis for the integral double-layer plate are analysed and derived by utilizing the theory of composite material mechanics and the theory of elastic thin plate. The result shows that the base structure will occur buckling failure if the longitudinal uniform pressure Nx ≥ (Nx)cr.
is more reasonable. After that, the expression of the flexural rigidity and the method of determining the position of the neutral axis for the integral double-layer plate are analysed and derived by utilizing the theory of composite material mechanics and the theory of elastic thin plate. The result shows that the base structure will occur buckling failure if the longitudinal uniform pressure Nx ≥ (Nx)cr.
沙漠地区日照充足,夏季炎热,冬季严寒,温度变化大。公路处于这样的环境条件中,受外界环境气温、太阳辐射等自然因素影响下及行车荷载作用下,造成沙漠区半刚性基层路面病害具有异于其他气候环境条件下的路面病害。在内蒙古自治区阿拉善盟沙漠地区某些路段不间断出现类似于“天然减速带”的横向隆起现象,当地人俗称“搓板路”,见图 1,开车即使慢速行驶,车身也颠簸不已,严重处路面横向隆起高度约10 cm,对行车安全构成极大的威胁,严重影响公路的通行能力与服务质量[1]。

|
| 图 1 内蒙古阿拉善地区路面横向隆起 Fig. 1 Pavement transverse blowup in Alxa Area, Inner Mongolia |
| |
路面的横向隆起病害常见于水泥混凝土路面,对于沥青混凝土路面隆起现象并不多见。美国阿肯色州关于水泥混凝土路面隆起的调查研究中,对水泥混凝土路面隆起的成因进行了分析,得出路面隆起总是发生在雨后7~14 d内的下午3点左右, 相对长混凝土板,短板发生隆起的几率较低, 位于具中高塑性指数、中等透水路基上的水泥混凝土路面易产生隆起现象等结论。基于此,认为混凝土路面的隆起与路面温度和湿度有关[2]。Arnold D. Kerr等假设水泥混凝土路面的隆起是由于路面内温度升高或湿度增大而引起的轴向力的作用所致,在此基础上建立了路面结构的屈曲失稳模型,分析了在自重和沿路面纵向作用力的共同作用下, 路面与基层间的抗力为近似双线性和非线性的情形下, 路面结构的胀后屈曲位移和轴向应力,并分别给出了温度和湿度增大而不使路面产生弯曲破坏的相应安全范围[3-4]。王华乔通过分析不同板厚、荷载和路基性质情况下路面板在行车荷载作用下出现的拱胀现象,并利用Theil和Van de Panne法探讨了路面板的应力和变形,并得出拱胀范围[5]。甘肃省交通运输厅测量队分析了甘肃省中西部干旱地区低级和过渡式路面搓板产生的原因主要在于表层材料稳定性不足,地区气候干旱,路基多系粉土及砾石戈壁,相对含水量小于0.3,路面厚度亦多在10 cm以上,承受车轮垂直力的整体强度都超过实际需要;路面表层抵抗水平推力的强度不足,在行车荷载作用下,粒料便产生位移堆积,容易形成隆起搓板现象[6]。黄保和等探讨了长间距胀缝与大长坡道上水泥混凝土路面的热胀屈曲稳定性,建立了以缩缝为界的短板的单体性屈胀力学模型,根据铁摩辛柯的弹性稳定理论,利用能量法求出临界纵向温度应力,并由此求出常用路面板的临界铺设温度,同时提出混凝土路面铺筑与养护的注意事项[7-10]。陈建康等针对有机玻璃和水泥混凝土两种路面模型,分别采用载波干涉法和千分表法研究了刚性路面热胀屈曲的力学机制与临界铺设温差并测量了临界压力;之后分析了温度作用下斜坡路面热胀失稳的力学原理,采用正则摄动法求解摄动方程并研究了斜坡路面与平直路面临界铺设温度差异的关系[11-12]。蒯行成等分析了刚性路面水泥稳定沙砾基层的热胀现象,提出在低温季节施工的基层应考虑胀缝设置,基层施工中要控制水泥用量[13]。徐宏等对水泥路面板在夏季高温隆起的原因进行探讨,计算了水泥路面板的压曲临界应力;通过举例计算板顶最大压应力,得出对于厚度26 cm左右的水泥路面板, 如胀缝设置不当,则旧水泥路面板在夏季将是危险的,且其在夏季出现隆起的临界板长约为85 m[14]。赵昕等采用材料力学中的压杆失稳理论和弹性力学中的薄板压曲理论对沥青混凝土路面的半刚性基层由温度引起拱胀发生的条件和状态进行了分析,根据半刚性基层拱胀破坏的临界应力与温度应力的大小比较,判别半刚性基层是否会发生拱胀[15]。李立寒等通过分析室内车辙试验试件、加速加载车辙试验路芯样, 以及沥青路面现场芯样的空隙率与高度变化, 证实了在车辆荷载作用下沥青层的隆起变形与松胀现象;分析了隆起变形在总车辙变形中所占的比例并给出了隆起系数的建议值范围为0~0.52[16]。
关于路面隆起病害现象的发生多见于水泥混凝土路面,对于沥青混凝土路面板结构层发生横向隆起病害现象并不多。因此,在前人研究的基础上,针对内蒙古自治区阿拉善盟沙漠区沥青混凝土路面不间断出现横向隆起的现象,基于相关力学理论,构建了沥青混凝土半刚性基层的隆起拱胀模型,分析基层结构在路面结构层自重和纵向均布压力作用下的挠曲与应力状态,便于控制路面、基层材料设计与施工控制。
1 力学模型依据沙漠区沥青混凝土路面横向隆起的实体物理模型和现场的实地调研分析,沙漠区沥青混凝土路面的局部隆起是由半刚性基层受纵向应力的作用下发生拱胀隆起。为此,将基层结构抽象简化为一四边简支、承受垂直于板面的竖向均布荷载q(x, y) (即路面结构层的自重)和沿路面纵向两端承受均匀分布压力的长矩形板,并考虑到实际工程基层中上基层与底基层的路用性能差异,假设该矩形板由材料性能、厚度均不同的2块各向同性单层板所构成。
为简化问题,在铁摩辛柯小挠度薄板理论的基础上做如下假定:
(1) 双层板各单层之间粘结良好,可作为一个整体结构板,不考虑双层板层间应力,认为各单层板之间变形连续。
(2) 板的总厚度仍符合薄板假定,即厚度t与跨度a之比为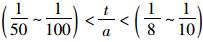
(3) 不考虑弯曲与拉伸耦合关系。
(4) 处于临界状态的路面如同悬浮在路基上,也就是路面板与地基间呈现似脱空非脱空状态,因此可认为路基支承在此时不起作用,即临界状态时路基反力不作考虑。
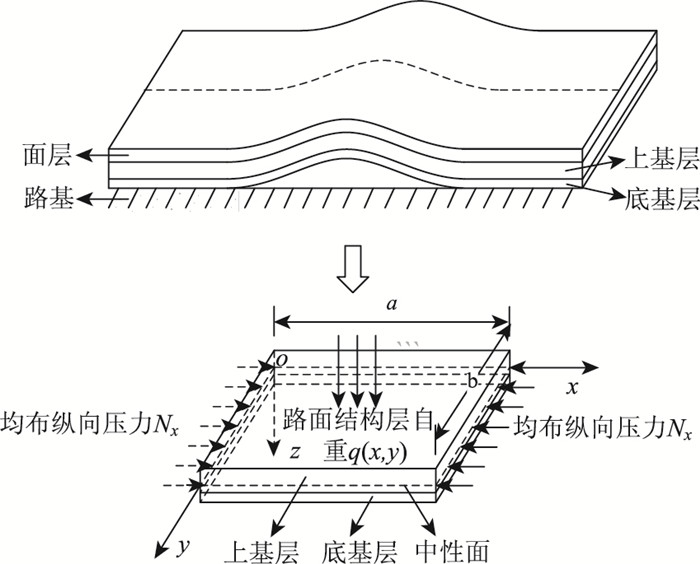
在上述假定的基础上,可采用单层板的屈曲失稳模型来分析上述双层板的受力,力学模型如图 2所示,其中,力学模型坐标系xoy平面为双层板中性面。
|
| 图 2 简支矩形双层板力学模型 Fig. 2 Mechanical model of simply supported rectangular double-layer plate |
| |
设双层板的抗弯刚度为D,在矩形板短边b上作用x方向的均匀分布的压力Nx(Nx为沿y轴方向每单位长度上的压力大小)。同时,矩形板承受方向竖直向下的均布荷载q(x, y),将均布荷载q(x, y)用三角级数表示为:
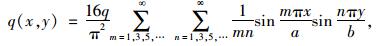
|
(1) |
式中,q为均布荷载q(x, y)集度;m, n为奇数1,3,5,…;a, b为矩形板的边长。
则双层板挠度w应满足微分方程
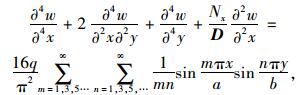
|
(2) |
以及屈曲的边界条件:
当x=0和x=a时, w=0,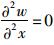
当y=0和y=b时, w=0,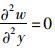
依据铁摩辛柯板壳理论所述,将矩形层合板挠度w取成如下级数形式[17]:
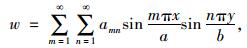
|
(3) |
则方程(2) 和简支边的边界条件都能满足,将此级数代入方程(2),可得:
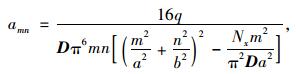
|
(4) |
式中,m和n是奇数1,3,5,…,如m和n中的一个为偶数,或两个都是偶数,则amn=0。因此板的挠度曲面为:
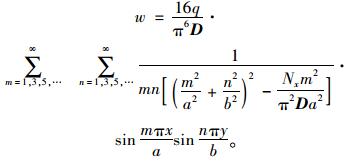
|
(5) |
由式(5) 可知,当Nx的值为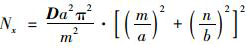
式(5) 中,Nx的最小值即为薄板失稳的临界压力,也即临界荷载。显然,Nx的临界值可由取n=1得到,进而有:
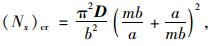
|
(6) |
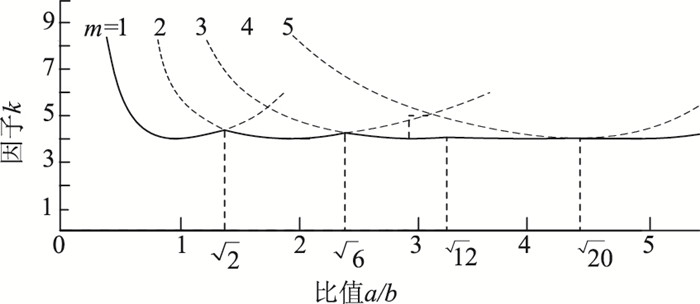
式中m应使式(6) 的值为最小。由比值a/b作因子k=(mb/a+a/mb)2的曲线图[17],得到如图 3所示曲线图。
|
| 图 3 不同m值情形下k与a/b关系 Fig. 3 Relationship between k and a/b with different values of m |
| |
图中,在决定k时所需要用的曲线部分由实线表示。可以看出,对于方形板以及任何可分割成整数个边长为b的正方形板,其因子k等于4;对于很长的板,k值趋近于4。考虑路面的实际情形,认为k值取为4比较合理,则有
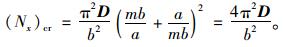
|
(7) |
由式(7) 可知,当Nx≥(Nx)cr,双层板即基层结构将发生失稳破坏,导致路面横向隆起的发生。
由式(7) 可知,该临界值与双层板抗弯刚度D有关,依据复合材料力学理论[18],在不考虑弯曲与拉伸耦合关系时,上述层合板弯曲刚度矩阵为:
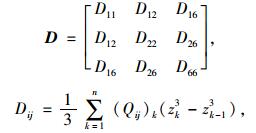
|
(8) |
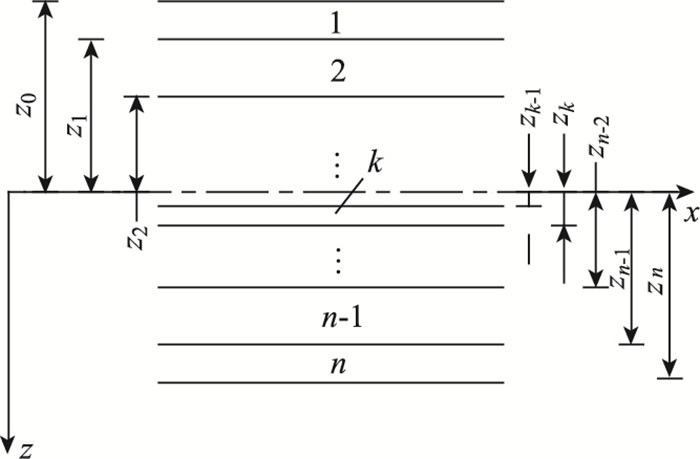
式中,Qij为表示与材料主方向成任意角度θ的x-y坐标系中的应力-应变关系的弹性矩阵中对应的元素;n代表组成层合板的单层板数目;zk为各单层板表面相对层合板中性面的坐标,如图 4所示。
|
| 图 4 层合板各单层z坐标 Fig. 4 z coordinate of each single layer of laminated plate |
| |
对于各向同性弹性板,平面应力状态下弹性矩阵为:
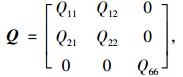
|
(9) |
式中,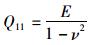
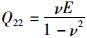
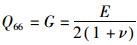
模型中双层板的抗弯刚度即为矩阵D中的D11,而D11的计算首先需确定层合板中性面的位置。根据所设假定,由弹性薄板理论[19]可知,不考虑板的横向正应力影响,用uz, ux, uy分别表示板横截面上任意一点在x, y, z方向的位移分量,则:
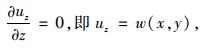
|
(10) |
忽略横向剪切,则γzx=γzy=0,根据几何方程得:
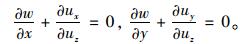
|
(11) |
求解上述偏微分方程并代入板中性面没有变形的条件可得:
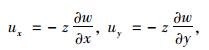
|
(12) |
式中z为板横截面上任意一点距板中性面的距离。
进而可得:
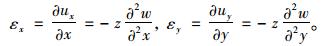
|
(13) |
将式(13) 应力状态的本构方程,可得:
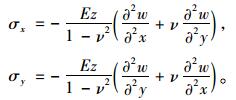
|
(14) |
不考虑层间应力,根据层合板横截面上沿x,y方向内力之和为0的条件,结合式(14) 可确定双层板中性面的位置[20],也就是半刚性基层中性面的位置,参照图 5有:
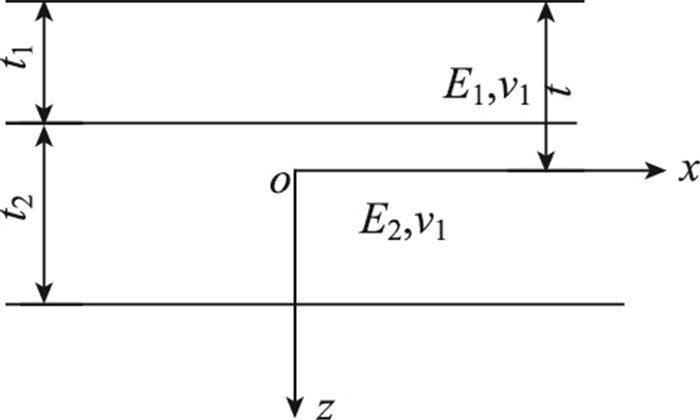
|
| 图 5 半刚性基层结构简图 Fig. 5 Schematic diagram of semi-rigid base structure |
| |
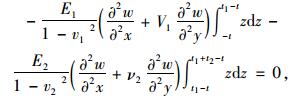
|
(15) |
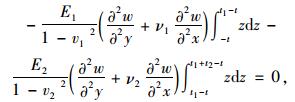
|
(16) |
式中, E1,E2及ν1, ν2分别为上基层与底基层的弹性模量和泊松比; t1, t2为上基层与底基层的厚度; t为半刚性基层上表面距基层中性面的距离。
将式(15)、(16) 两式相加,可得:
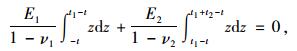
|
(17) |
求解该积分可得:
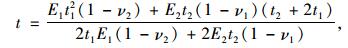
|
(18) |
进而可得:
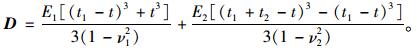
|
(19) |
将式(19) 代入式(7),可知沥青混凝土路面半刚性基层的临界荷载为:
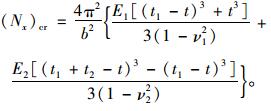
|
(20) |
沙漠区某公路半刚性基层受温度应力作用产生路面横向隆起病害。采取该路面结构参数,依据文中推导公式,分析路面产生横向隆起病害的临界荷载。结构参数如表 1所示。
| 基层宽度 b/m |
基层厚度/cm | 基层模量/MPa | 基层泊松比 | |||||
| 上基层t1 | 底基层t2 | 上基层E1 | 底基层E2 | 上基层ν1 | 底基层ν2 | |||
| 12 | 30 | 20 | 1 500 | 700 | 0.25 | 0.35 | ||
将上述参数代入式(18)
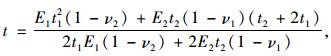
|
可得中性面到基层上边缘的距离t≈21.6 cm, 之后将t的值代入式(20)。
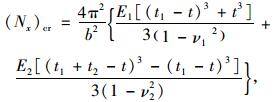
|
可得路面半刚性基层结构受纵向荷载作用下发生横向隆起病害的临界荷载(Nx)cr=3.29×106 N/m。
由以上分析可知,当纵向压力Nx≥(Nx)cr,半刚性基层双层板(上基层和底基层)会出现失稳破坏并导致沥青路面产生横向隆起病害。显然,在已知各路面基层结构的弹性模量、泊松比、尺寸的情形下,就可依据式(17) 和式(19) 推导沥青混凝土路面基层隆起拱胀模型的失稳临界荷载(Nx)cr, 进而可分析致使路面横向隆起病害发生的纵向力的影响因素,减少或降低不利因素的影响,防止路面横向隆起病害的发生。对于由温度应力引起的路面结构层横向隆起病害,温度应力的大小与路面结构层的材料组成设计密切相关,通过进一步分析研究温度应力与结构层材料组分及自然环境之间的内在规律,可指导路面结构层的材料组成设计与现场施工。
4 结论沙漠地区气候环境等自然条件相对比较特殊,沥青路面结构层受外界环境影响产生路面横向隆起病害,严重影响行车的安全性与舒适性,病害的进一步发展会导致路面发生结构性破坏,缩短服务寿命,增加维修养护成本。根据横向隆起病害的实体特征,结合弹性薄板与复合材料力学相关理论,将沥青路面基层简化为一四边简支的双层层合板的隆起拱胀力学模型,推导了沥青混凝土路面基层在竖向均布荷载和纵向均布压力共同作用下发生横向隆起拱胀的临界荷载公式。根据此公式,可进一步分析导致病害产生的纵向力的影响因子及相互影响规律,从而可指导路面结构的材料组成设计与现场施工,为隆起病害防治提供理论基础。
| [1] | 张宏, 王智远, 张海龙, 等. 阿拉善额济纳地区公路盐胀病害成因分析[J]. 安全与环境学报, 2015, 15(6): 151-154 ZHANG Hong, WANG Zhi-yuan, ZHANG Hai-long, et al. Analysis of Desert Highway Expansion Caused by the Excessive Salt Content in Ejina of Alxa Area, Inner Mongolia[J]. Journal of Safety and Environment, 2015, 15(6): 151-154 |
| [2] | HENSLEY M J. The Study of Pavment Blowups[M]. Little Rock: Arkansas State Highway Department, 1966. |
| [3] | KERR A D, DALLIS W A Jr. Blowup of Concrete Pavements[J]. Journal of Transportation Engneering, 1985, 111(1): 33-53 |
| [4] | KERR A D, SHADE P J. Analysis of Concrete Pavement Blowups[J]. Acta Mechanica, 1984, 52(3/4): 201-224 |
| [5] | 王华桥, 周纯祖. 刚性路面的拱胀[J]. 中外公路, 1989(6): 41-43 WANG Hua-qiao, ZHOU Chun-zu. The Blowup of Rigid Pavement[J]. Journal of China and Foreign Highway, 1989(6): 41-43 |
| [6] | 甘肃省交通厅测量队. 甘肃省公路路面搓板防治经验[J]. 公路, 1964(1): 34-37 Survey Team of Gansu Transport Department. The Prevention Experiences of Highway Pavement Hump in Gansu[J]. Highway, 1964(1): 34-37 |
| [7] | 黄保和, 朱照宏. 水泥混凝土路面的热胀屈曲稳定性分析[J]. 同济大学学报:自然科学版, 1984(3): 65-78 HUANG Bao-he, ZHU Zhao-hong. Stability Analysis of Thermal Expansion Buckling in Concrete Pavement[J]. Journal of Tongji University:Natural Science Edition, 1984(3): 65-78 |
| [8] | 黄保和. 长大坡道上水泥砼路面热胀屈曲稳定性初步分析[J]. 华东公路, 1985(4): 19-24 HUANG Bao-he. Preliminery Analysis of Thermal Expansion Buckling Stability in Concrete Pavement Located in Long Steep Grade[J]. East China Highway, 1985(4): 19-24 |
| [9] | 黄保和. 长间距胀缝水泥混凝土路面的铺筑和养护[J]. 华东公路, 1989(5): 12-17 HUANG Bao-he. Construction and Maintainence of Concrete Pavement with Long-spaced Expansion Joint[J]. East China Highway, 1989(5): 12-17 |
| [10] | 黄保和. 长间距胀缝水泥混凝土路面的热胀屈曲稳定性分析[J]. 中国公路学报, 1991(3): 32-40, 23 HUANAG Bao-he. An Analysis of the Stability from Thermal Expansion Buckling Stress for Concrete Pavement with Long-spaced Expansion Joint[J]. China Journal of Highway & Transport, 1991(3): 32-40, 23 |
| [11] | 王汝鹏, 陈建康. 刚性路面热胀屈曲的实验分析[J]. 力学季刊, 1991(3): 55-62 WANG Ru-peng, CHEN Jian-kang. The Experiment Method to Study the Thermal Buckling of Stiff Pavements[J]. Chinese Quarterly of Mechanics, 1991(3): 55-62 |
| [12] | CHEN Jian-kang, WANG Ru-peng. Perturbation Solution for Thermal Expansion Buckling of No Expansion Joint Slope Pavement Plate[J]. Applied Mathematics and Mechanics, 1993, 14(3): 277-284 |
| [13] | 蒯行成, 袁太平. 水泥砼路面及水泥稳定砂砾基层热胀问题的分析[J]. 中南公路工程, 2001, 26(3): 6-8 KUAI Xing-cheng, YUAN Tai-ping. Analysis of Thermal Expansion Buckling against Cement Concrete Pavemeng and Cement Stabilized Sand Base[J]. Central South Highway Engineering, 2001, 26(3): 6-8 |
| [14] | 徐宏, 邓学钧, 倪富健. 水泥路面板高温隆起的力学机理分析[J]. 公路交通科技, 2008, 25(11): 1-5 XU Hong, DENG Xue-jun, NI Fu-jian. Analysis of Mechanical Behavior of Pavement Slab Humping by High Temperature[J]. Journal of Highway and Transportation Research and Development, 2008, 25(11): 1-5 |
| [15] | 赵昕, 沙爱民, 洪斌. 半刚性基层拱胀现象的力学分析[J]. 公路交通科技, 2008, 25(4): 42-46 ZHAO Xin, SHA Ai-min, HONG Bin. Mechanical Analysis of Vaulted Expansion of Semi-rigid Base[J]. Journal of Highway and Transportation Research and Development, 2008, 25(4): 42-46 |
| [16] | 李立寒, 陈建军, 苏洲, 等. 沥青层隆起变形与松胀现象分析[J]. 同济大学学报:自然科学版, 2009, 37(1): 52-56 LI Li-han, CHEN Jian-jun, SU Zhou, et al. Analysis of Uplift Deformation and Loose Phenomena of Asphalt Layer[J]. Journal of Tongji University:Nature Science Edition, 2009, 37(1): 52-56 |
| [17] | 铁摩辛柯S, 沃诺斯基S. 板壳理论[M]. 2版. 北京: 科学出版社, 1977. TIMOSHENCO S, WOINOWSKY S. Theroy of Plates and Shells[M]. 2nd ed. Beijing: Science Press, 1977. |
| [18] | 陈明祥. 弹塑性力学[M]. 北京: 科学出版社, 2007. CHEN Ming-xiang. Elasticity and Plasticity[M]. Beijing: Science Press, 2007. |
| [19] | 沈观林, 胡更开, 刘彬. 复合材料力学[M]. 2版. 北京: 清华大学出版社, 2006. SHEN Guan-lin, HU Geng-kai, LIU Bin. Mechanics of Composite Materials[M]. 2nd ed. Beijing: Tsinghua University Press, 2006. |
| [20] | 邓学钧. 路基路面工程[M]. 3版. 北京: 人民交通出版社, 2009. DENG Xue-jun. Road Subgrade and Pavement Engineering[M]. 3rd. ed. Beijing: China Cummunications Press, 2009. |
 2017, Vol. 34
2017, Vol. 34
