扩展功能
文章信息
- 齐琳, 姚俭, 王心月
- QI Lin, YAO Jian, WANG Xin-yue
- 基于改进粒子群算法的电动汽车充电站布局优化
- Optimizing Layout of Electric Vehicle Charging Station Based on Improved Particle Swarm Optimization Algorithm
- 公路交通科技, 2017, 34(6): 136-143
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(6): 136-143
- 10.3969/j.issn.1002-0268.2017.06.020
-
文章历史
- 收稿日期: 2016-09-19
充电站布局优化问题是国家建设电动汽车充电基础设施的发展规划问题。目前我国新能源汽车产业正加速发展,新能源汽车产业的快速发展能为全社会提供福利,但其基础设施的缺乏是成为限制新能源汽车产业发展的主要瓶颈[1]。因此,研究如何科学地规划充电站的地理位置,使整个社会获得最大的经济效益,具有重要的现实意义。国内外很多学者利用启发式算法寻求充电站布局规划的满意解,如量子遗传算法[2]、模拟退火算法[3]、量子粒子群算法[4]、差分进化粒子群算法[5]等。这些智能算法多用于求解充电站运营方单方面问题,在考虑充电站运营方和用户方多方面的充电站选址规划问题中用途较少。随着电动汽车市场的不断发展,仅考虑充电站运营方单方面优化问题说服力较小,因此研究充电站运营方和用户方双方整体经济效益最大化是未来的趋势。
K中心点聚类算法是把多个对象划分成多个组或“聚簇”,从而使相同集合内的对象非常相似而不同集合内的对象完全不同的数据挖掘算法[6]。K中心点聚类算法具有简单、抗噪能力和局部搜索能力强的优势[7]。李德毅院士[8]提出了一种定性信息转换成定量信息的云模型。国内外许多学者将云模型算法和智能算法结合,常见的智能算法有蚁群算法[9]和混合粒子群优化算法[10]等。云模型可提高智能算法的全局收敛能力; 而粒子群算法有实现容易、精度高、收敛快等优点,但也存在着粒子越来越相似、在局部得到最优解、在周边无法退出等缺点。文中针对带有充电站服务要求和用户需求限制的充电站布局优化问题,在K中心点聚类算法、云模型算法、粒子群算法的基础上,吸收3种方法的优势和长处,克服劣势和缺陷,进而提出基于K中心点云模型混合自适应粒子群算法,并通过算例计算,验证其求解性能。
1 带有充电站服务要求和用户充电需求限制的充电站布局优化模型 1.1 问题描述在电动汽车领域,充电站布局要满足充电站运营商的盈利需求,并兼顾充电用户的利益。充电站的建设位置直接影响充电站的服务效果,因此充电站布局要符合交通流中的汽车运行分布规律。充电站布局优化的目标是在满足充电站服务要求和用户充电需求的前提下,建立数学模型,使充电站服务成本和用户充电需求成本之和最小。充电站服务成本包括充电站规划建设投资成本、人力成本、充电站维护成本、充电站故障成本。用户充电需求成本包括用户购电成本、用户路途成本、用户充电等待时间成本。文中所讨论的问题必须满足如下约束。
充电机配置约束:每个充电站充电机的配置数量应在一定范围内。
总车流量约束:每个充电站区域的总车流量应在一定范围内。
节点充电站数量约束:每个节点建设充电站个数最多为1个。
总充电站数量约束:所有节点所建立的充电站总数量要小于规划内的最大可建充电站数量。
充电站服务半径约束:充电站的服务半径要在一定范围内。
充电站密度约束:相邻充电站间距不能过小。
充电站充电负荷约束:充电站充电机充电负荷要大于规划区内的电动汽车充电负荷。
充电站充电功率约束:充电站的充电功率要满足接入充电汽车的充电额定功率。
1.2 符号定义与数学模型下面对带有充电站服务要求和用户充电需求限制的充电站布局优化问题建立数学模型。
C为社会总投入成本;Cfc为充电站投资成本;Cps为人员工资成本;Cdm为充电站维护成本;Cbm为充电站故障成本;Cbe为用户购电成本;Cdw为用户快充路途成本;Caw为用户充电等待时间成本;Vi为第i个充电站; Nbci为第i个充电站充电机的配置数量;α为和充电机有关的投资系数;w为建筑道路等固定不变的建设投资;r为贴现率;n为充电站的运行年限;p为每台充电机的平均人员工资;q为每台充电机的平均维护费用;l为过电流保护费用;v为过压保护费用;s为过热保护费用;Cr为充电站平均每次故障单位时间检修成本;Tr为充电站发生故障平均检修时间;Cl为充电站平均每次故障单位时间惩罚成本;Tc为充电站发生故障平均持续时间;Nk为充电站充电机年均故障次数; k为需求点数量;β为电动汽车用户在充电站充电机上充电的单位价格;e为电动汽车用户每次充满1辆电动汽车所需的用电量;Nj为1辆电动汽车年均充电次数;fij为在第i个充电站第j个需求点的车流量;uij为在第i个充电站第j个需求点的停车量;dij为电动汽车用户从第j个需求点行驶到第i个充电站的距离;ek为电动汽车每小时耗电量;δ为充电汽车用户在充电过程中等待的单位时间成本;Tf为充电汽车用户在充电过程中平均等待时间;Nbcmin为最小充电站的数量;Nbcmax为最大充电站的数量;fmin为每个充电站区域的总车流量最小值;Wn为每个节点充电站的数量;Wmax为规划内最大可建充电站的数量;Mn为节点数量;dmax为充电站的最大服务半径;djk为相邻充电站间的距离;Pi为第i个充电站充电机的充电负荷;P为规划区内电动汽车的充电负荷;Pc为充电汽车的额定功率;Pemax为充电站充电机的充电功率。
决策变量:

|
数学模型:
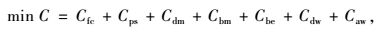
|
(1) |
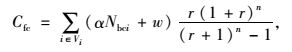
|
(2) |
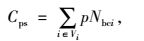
|
(3) |
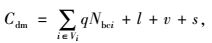
|
(4) |
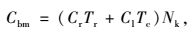
|
(5) |
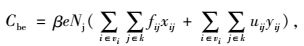
|
(6) |
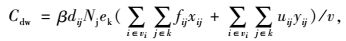
|
(7) |
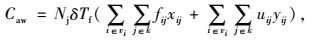
|
(8) |
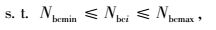
|
(9) |

|
(10) |
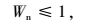
|
(11) |
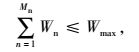
|
(12) |
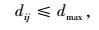
|
(13) |
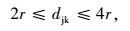
|
(14) |
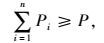
|
(15) |
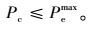
|
(16) |
模型中,式(1) 为社会总投入成本目标函数;式(2)~(8) 分别为各充电站运营方和用户方的投入成本;式(9) 表示每个充电站充电机的配置数量应在一定范围内;式(10) 表示每个充电站区域的总车流量应在一定范围内;式(11) 表示每个节点建设充电站个数最多为1个;式(12) 表示所有节点所建立的充电站总数量要小于规划内的最大可建充电站数量;式(13) 表示充电站的服务半径要在一定范围内;式(14) 表示相邻充电站间距离不能过于密集;式(15) 表示充电站充电机充电负荷要大于规划区内电动汽车的充电负荷;式(16) 表示充电站充电机充电功率要满足接入的充电汽车额定功率。
2 K中心点云模型混合自适应粒子群算法的设计 2.1 K中心点聚类算法K中心点聚类算法目标是使式(7) 的函数达到最小。
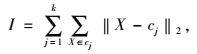
|
(17) |
式中,k为聚类组个数; cj为第j个聚类的中心; I为各粒子X同与它最近的聚簇中心点cj之间的距离平方和。
K中心点聚类算法的主要逻辑思想是:选取K个初始点作为初始类簇中心点,挑选初始中心点采用随机抽取方式,通过随机选取初始点来启动算法,根据其余对象与每个类簇中心点的相异度之和,将每个对象分离到离其最近的类簇中心点所代表的类簇中,重新用非中心点代表类簇的中心点,不断优化聚类效果,直到达到指定的迭代次数。
K中心点算法与K-means算法都是数据挖掘聚类算法,都可以对样本进行分类。用K中心点法而不用K-means算法,是由于K中心点法不受噪声和孤立点所影响,且对聚类中心的初始位置不敏感。
2.2 云模型自适应粒子群算法 2.2.1 云模型算法云模型是李德毅院士提出的定性与定量相互转换的一种新模型。云模型的不确定性的特点和自然界中智能算法的进化原则相似。
云模型定义:假设有一维或多维的用精确值来表示的论域U,A是U上对应着的定性概念,存在随机数y=uA(x),其中,y为随机数;uA(x)为x在U上的分布[11]。
云模型算法描述:云模型用Ex, En, He这3项指标来表示,Ex为个体继承的优秀因子; En为进化熵,代表个体进化变异的区间范围; He为进化超熵,表征个体进化变异的稳定性范围,He越大则不确定性越大[12]。
2.2.2 基本粒子群算法粒子群算法是一种全局搜索的智能优化算法,是最早由Kennedy和Eberhart在1995提出的模拟鸟类捕食行为的进化算法[13]。假设在D维空间内,有种群样本X=(X1, X2, …, Xn),第i个粒子位置为Xi=(xi1, xi2, …, xid)T,第i个粒子速度为Vi=(vi1, vi2, …, vid)T,粒子根据式(18)~(19) 来更新自己的速度和新的位置,直到达到终止条件,终止迭代,输出当前最优解。
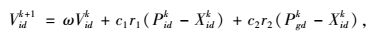
|
(18) |
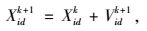
|
(19) |
式中,ω为惯性权重;c1和c2为学习因子;r1和r2为取值在[0, 1]区间内均匀分布的随机数;Pidk为个体所经历位置中适应度值最优的位置;Pgdk为所有粒子在解空间搜索到的适应度值最优位置;Xidk为第i个粒子在d维空间第k次寻优值的位置;Vidk为第i个粒子在d维空间第k次寻优的速度。
2.3 改进粒子群算法解决电动汽车充电站布局优化问题的创新点针对带有充电站服务要求和用户充电需求限制的充电站布局优化问题,提出电动汽车充电站布局优化的数学模型。采用与电动汽车充电站布局相似的Voronoi图划分电动汽车充电站的服务范围,保证服务范围内的充电汽车需求点到该充电站的距离小于到其他充电站的距离。Voronoi图按照最邻近原则划分平面,Voronoi图的思想与研究内容相符,故采用Voronoi图划分充电汽车充电站的服务范围。但Voronoi图是划分部分区域的局部最优,不适用于全局寻优。故引入具备全局寻优能力的改进粒子群算法求解问题。
云模型和粒子群相结合是改进粒子群算法惯性权重大小的一种策略[14]。云模型可将定性信息转为定量信息,又有易于与其他方法结合的特点,故云模型多用来控制智能进化算法的参数,完成算法的优化。所以云模型算法适于改进粒子群算法。云模型自适应算法先求出第t次迭代粒子群体搜索到的极值信息和单个粒子在第t代的适应度值的比值,用此比值将种群划分为3个区域,每个区域里的种群位置和速度更新时分别采用不同惯性权重W,其中种群离全局最优值较远时,为提高全局搜索能力,让粒子快速向最优解位置靠拢,粒子速度更新时用较大惯性权重;种群离全局最优值较近时,为提高局部搜索能力,让粒子更精确地向最优解位置靠拢,速度更新时用较小惯性权重;种群处于中间范围时,其位置处于不确定状态,用云模型将粒子不确定的定性信息转换成确定的定量信息,进行惯性权重的调整。
云模型自适应粒子群算法在实现过程中,粒子种群利用个体极值以及种群极值信息快速地向在全局最优解所在区域靠拢。粒子种群的这一特点使粒子群算法有高效的搜索能力,但用粒子搜索解空间内的全局最优解时,会过分依赖个体极值信息,使粒子越来越相似,越来越趋于同化,在局部得到最优解时,粒子无法跳出局部最优。为克服此缺陷,本文提出一种新算法对粒子的个体极值信息先进行聚类分析,利用聚类后形成的类簇中心点的适应度值和此粒子适应度的比值将种群划分,从而分配惯性权重。通过这样的改进方法,粒子在所在类簇的中心点附近进行局部搜索,避免种群因为过分依赖极值信息而同质化,这样可以维持粒子个体差异,增加种群多样性,更精确地分配惯性权重,从而更有效率地搜索到最优解。
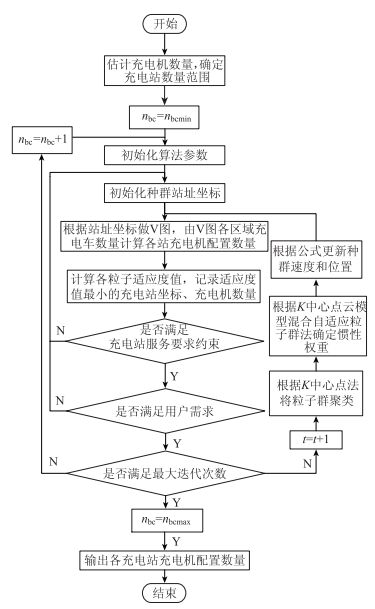
2.4 K中心点云模型混合自适应粒子群算法的步骤结合K中心点聚类法和云模型自适应粒子群算法,构建求解充电站布局优化问题的K中心点云模型混合自适应粒子群算法,其流程图如图 1所示。
|
| 图 1 算法流程图 Fig. 1 Flowchart of algorithm |
| |
K中心点云模型混合自适应粒子群算法优化步骤如下。
步骤1:根据式(20)~(23) 估计充电机数量,确定充电站范围。式中,τ为充电汽车充电功率;Tc为1辆电动汽车充满电所需时间;p为充电机功率;η为充电效率;Tm充电机持续充电时间;nbc为充电站的数量;nbcmin和nbcmax分别为充电站数量的最小值和最大值;Nbcmin和Nbcmax分别为充电机数量的最小值和最大值。
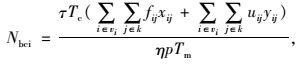
|
(20) |
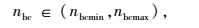
|
(21) |
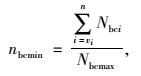
|
(22) |
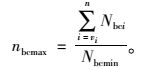
|
(23) |
步骤2:从充电站数量最小值开始循环。
步骤3:初始化算法参数,确定粒子种群数Sizepop和最大迭代次数Maxgen。
步骤4:初始化种群站址坐标。
步骤5:根据站址坐标做Voronoi图,由Voronoi图各区域电动汽车数量计算各站充电机的配置数量。Voronoi图是广泛应用于地理设施选址、充电站选址定容的一种工具[15]。它按最邻近原则将平面划分为多个区域,每个点与其最临近的区域相关联。充电站规划符合Voronoi图的特点,因此,文中用Votonoi图方法来将各需求点分配到离其最近的充电站。
步骤6:计算各粒子适应度值,记录适应度值最小的充电站坐标、充电机数量。若满足充电机配置(9)、总车流量(10)、节点充电站数量(11)、总充电站数量(12)、充电站服务半径(13)、充电站密度(14)、充电站充电负荷(15)、充电站充电功率(16) 等约束条件,转步骤7;否则,转步骤4。
步骤7:若满足最大迭代次数,转步骤11,否则,转步骤8。
步骤8:使t=t+1,选取3个粒子xi作为3个K中心点聚类中心Ci的初始点,每个聚类Cj的中心为ci=(xi1, xi2, …, xid)T,计算两点间的欧式距离,若满足式(17),xi将属于Cj,将所有粒子按此方法分配完。
步骤9:计算第t次迭代粒子所属聚类中心结合Cj的中心点的适应度值和单个粒子在第t代的适应度值的比值,用此比值将种群划分为3个区域,其中种群离全局最优值较远时,为提高全局搜索能力,粒子速度更新时用较大惯性权重,惯性权重值取0.9;种群离全局最优值较近时,为提高局部搜索能力,粒子速度更新时用较小惯性权重,惯性权重取0.4;种群处于中间范围时,其位置处于不确定状态,用云模型调整惯性权重。
步骤10:根据式(18)~(19) 更新种群速度和位置,转步骤5。
步骤11:若充电站数量已是最大值,转步骤12,否则,使nbc=nbc+1,转步骤3。
步骤12:输出当前最优解。
3 改进算法的算例仿真为测试改进算法的可行性,针对文中提出的优化充电站布局方法,为简化计算,选取一个由25个需求点组成的区域进行算例仿真[16]。
算例仿真中各参数设定情况如下:充电站充电机配置数量范围从4台到13台,每个需求点的车流量和固定停车量如表 1所示,电动汽车功率为25 kW,每辆电动汽车充电时间为0.5 h,充电机的充电功率为500 kW,充电效率为90%。充电站投资成本中,充电机的投资系数为8万元,建筑道路等固定不变投资建设费用为400万元,贴现率为5%,运行年限为15 a。人员工资成本是充电机配置数量的函数,为线性增函数,系数为50 000。充电站维护成本为充电机配置数量的增函数,系数为60 000,过流保护费用为1 000元,过压保护费用为1 000元,过热保护费用为1 000元,充电站故障成本中平均每次检修成本为1万元,惩罚成本为0.5万元,平均每次检修时间为2 h,惩罚持续时间为4 h,平均每年故障发生9次。用户购电成本中,单位电价为0.5元/(kW·h),年均充电次数为150次。用户路途成本中,每小时耗电量为25 kW·h。
| 需求点i | 坐标X | 坐标Y | 车流量/veh | 停车量/veh |
| 1 | 0.39 | 10.34 | 42 | 8 |
| 2 | 8.70 | 3.42 | 57 | 13 |
| 3 | 16.64 | 18.77 | 34 | 17 |
| 4 | 12.35 | 11.81 | 44 | 5 |
| 5 | 10.40 | 8.81 | 28 | 8 |
| 6 | 17.28 | 18.84 | 53 | 11 |
| 7 | 1.95 | 13.12 | 19 | 6 |
| 8 | 18.16 | 9.04 | 39 | 9 |
| 9 | 2.16 | 16.80 | 31 | 14 |
| 10 | 10.34 | 10.65 | 20 | 7 |
| 11 | 2.86 | 11.08 | 23 | 11 |
| 12 | 11.19 | 13.60 | 37 | 8 |
| 13 | 0.09 | 7.34 | 41 | 7 |
| 14 | 15.33 | 4.79 | 36 | 15 |
| 15 | 16.97 | 11.58 | 33 | 9 |
| 16 | 18.34 | 17.34 | 23 | 7 |
| 17 | 19.74 | 8.14 | 29 | 4 |
| 18 | 10.10 | 2.25 | 38 | 10 |
| 19 | 5.43 | 8.88 | 42 | 5 |
| 20 | 2.02 | 6.00 | 26 | 9 |
| 21 | 10.16 | 8.03 | 32 | 14 |
| 22 | 11.71 | 16.67 | 37 | 11 |
| 23 | 15.26 | 8.07 | 27 | 9 |
| 24 | 1.66 | 7.80 | 29 | 13 |
| 25 | 13.23 | 7.21 | 30 | 10 |
文中利用MATLAB R2011a对K中心点云模型混合自适应粒子群算法进行编程实现,3种算法在Intel Core(TM)i-2410M CPU @ 2.30GHZ 2.30处理器上运行。为便于比较3种算法的结果,将参数设置为相同的值,粒子种群数Sizepop=20,最大迭代次数Maxgen=300次,学习因子c1=1.494 45,学习因子c2=1.494 45,惯性权重最大值ws=0.9,惯性权重最小值we=0.4。
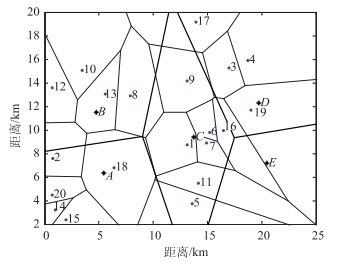
用K中心点云模型混合自适应粒子群算法求出的社会总投入成本为3 988 960元,最优建设充电站个数为5个,充电站A, B, C, D, E规划的充电机数量分别为9,5,11,6,4个,最优充电站规划图如图 2所示(数字表示需求点,字母表示充电站)。
|
| 图 2 充电站选址最优规划图 Fig. 2 Optimal planning of charging station location |
| |
改进算法的创新之处在于云模型自适应粒子群算法中引入K中心点聚类算法,它可有效改善粒子越来越相似、越来越趋于同质化、陷入局部区域的缺陷,可增强粒子的多样性。改进后的粒子群算法在时间上可更快地解决电动汽车充电站的布局优化问题,优化结果使得充电站成本和用户充电成本更小,结果更精确[17]。文中所设计的K中心点云模型混合自适应粒子群算法是求解带有充电站服务要求和用户充电需求限制的充电站布局优化问题的一种有效算法。
3种算法的优化结果如表 2所示。基本粒子群算法求出的社会总投入成本为5 273 935元,最优建设充电站个数为8个,算法运行耗时73.31 s;云模型自适应粒子群算法社会总投入成本为403 367元,最优建设充电站个数为6个,算法运行耗时61.49 s;K中心点云模型混合自适应粒子群算法求出的社会总投入成本为3 988 960元,最优建设充电站个数为5个,算法运行耗时59.58 s。由此可看出,改进的云模型自适应粒子群算法和K中心点云模型混合自适应粒子群算法都比基本粒子群算法更有效率,其求得的解均优于基本粒子群算法,并且K中心点云模型混合自适应粒子群算法更优于云模型自适应粒子群算法。
| 算法 | 基本粒子群 算法 | 云模型自适应 粒子群算法 |
K中心点云模 型混合自适应 粒子群算法 |
| 社会总投入成本/元 | 5 273 935 | 4 233 670 | 3 988 960 |
| 充电站个数/个 | 8 | 6 | 5 |
| 算法耗时/s | 73.31 | 61.49 | 59.58 |
4 结论
电动汽车的大规模推广和充电站的建设之间有密切关系[18],充电站布局需考虑多方面条件。文中针对带有充电站服务要求和用户充电需求限制的充电站布局优化问题建立了模型,将与充电站布局相似的Voronoi图方法、K中心点聚类算法和云模型自适应粒子群算法相结合,扬长避短,提出了K中心点云模型混合自适应粒子群算法。算例仿真表明,所用方法确实比基本粒子群等算法在求解充电站优化问题方面速度快,结果更优化。文中模拟了实际中的电动汽车分布不均匀的特点,自动划分了充电站的服务范围,自动分配了最优的充电站数量及最优位置,使充电站服务成本与用户充电成本之和最小。
文中提出的K中心点云模型混合自适应粒子群算法不仅在解决充电站布局优化问题上是一种有效的方法,而且其创新性也为改进粒子群等智能进化算法提供了一种新思路。
| [1] | MADINAA C, ZAMORAB I, ZABALA E. Methodology for Assessing Electric Vehicle Charging Infrastructure Business Models[J]. Energy Policy, 2016, 89: 284-293 |
| [2] | 黄小庆, 杨夯, 陈颉. 基于LCC和量子遗传算法的电动汽车充电站优化规划[J]. 电力系统自动化, 2015, 39(17): 323-332 HUANG Xiao-qing, YANG Hang, CHEN Xie. Optimal Planning of Electric Vehicle Charging Stations Based on Life Cycle Cost and Quantum Genetic Algorithm[J]. Automation of Electric Power System, 2015, 39(17): 323-332 |
| [3] | 加鹤萍, 谢胜利, 邵翔. 基于模拟退火算法的城市电动汽车充电站优化布局[J]. 山西电子技术, 2013(3): 26-28 JIA He-ping, XIE Sheng-li, SHAO Xiang. The Location Model of the Electric Vehicle Charging Station Based on Simulated Annealing Algorithm[J]. Shanxi Electronic Technology, 2013(3): 26-28 |
| [4] | 刘自发, 张伟, 王泽黎. 基于量子粒子群优化算法的城市电动汽车充电站优化布局[J]. 中国电机工程学报, 2012, 32(22): 39-45 LIU Zi-fa, ZHANG Wei, WANG Ze-li. Optimal Layout of Electric Vehicle Charging Station Based on Quantum Particle Swarm Optimization Algorithm[J]. Proceedings of the Chinese Society for Electrical Engineering, 2012, 32(22): 39-45 |
| [5] | 赵书强, 李志伟. 基于差分进化粒子群算法的城市电动汽车充电站最优规划[J]. 华北电力大学学报, 2015, 42(2): 1-7 ZHAO Shu-qiang, LI Zhi-wei. Optimal Planning of Charging Station for Electric Vehicle Based on PSODE Algorithm[J]. Journal of North China Electric Power University, 2015, 42(2): 1-7 |
| [6] | 李文波, 吴素研. 数据挖掘十大算法[M]. 北京: 清华大学出版社, 2013. LI Wen-bo, WU Su-yan. Ten Algorithms for Data Mining[M]. Beijing: Tsinghua University Press, 2013. |
| [7] | 李猛, 王道波, 盛守照. 基于加权k-均值聚类与粒子群优化的多航迹规划[J]. 系统工程与电子技术, 2012, 34(3): 512-517 LI Meng, WANG Dao-bo, SHENG Shou-zhao. Multiple Route Planning Based on Particle Swarm Optimization and Weighted k-means Clustering[J]. System Engineering and Electronic Technology, 2012, 34(3): 512-517 |
| [8] | QIN K, XU K, LIU F, LI D. Image Segmentation Based on Histogram Analysis Utilizing the Cloud Model[J]. Computers & Mathematics with Applications, 2011, 62(7): 2824-2833 |
| [9] | 牟峰, 王慈光, 袁晓辉. 基于云模型的参数自适应蚁群遗传算法[J]. 系统工程与电子技术, 2009, 31(7): 1763-1767 MOU Feng, WANG Ci-guang, YUAN Xiao-hui. ACGA with Adapting Parameters Based on Cloud Models[J]. System Engineering and Electronic Technology, 2009, 31(7): 1763-1767 |
| [10] | LI M W, HONG W C, KANG H G. Ban Traffic Flow Forecasting Using Gauss-SVR with Cat Mapping, Cloud Model and PSO Hybrid Algorithm[J]. Neurocomputing, 2013, 99(1): 230-240 |
| [11] | 刘常昱. 正态云模型的统计分析[J]. 信息与控制, 2005, 34(2): 236-239 LIU Chang-yu. Some Statistical Analysis of the Normal Cloud Model[J]. Information and Control, 2005, 34(2): 236-239 |
| [12] | 张光卫, 何锐, 刘禹. 基于云模型的进化算法[J]. 计算机学报, 2008, 31(7): 1082-1090 ZHANG Guang-wei, HE Rui, LIU Yu. An Evolutionary Algorithm Based on Cloud Model[J]. Chinese Journal of Computers, 2008, 31(7): 1082-1090 |
| [13] | KENNEDY J, EBERHARTR C. Particle Swarm Optimization[C] //Proceedings of IEEE International Conference on Neural Networks. Perth, Australia: IEEE, 1995: 1942-1948. |
| [14] | 徐红洋, 田雨波, 黄太安. 基于云变异的云自适应粒子群算法[J]. 计算机仿真, 2012, 29(11): 251-256 XU Hong-yang, TIAN Yu-bo, HUANG Tai-an. Cloud Adaptive Particle Swarm Optimization Algorithm Based on Cloud Variation[J]. Computer Simulation, 2012, 29(11): 251-256 |
| [15] | 葛少云, 李慧, 刘洪. 基于加权Voronoi图的变电站优化规划[J]. 电力系统自动化, 2007, 31(3): 29-33 GE Shao-yun, LI Hui, LIU Hong. Substation Optimization Planning Based on the Weighted Voronoi Diagram[J]. Automation of Electric Power System, 2007, 31(3): 29-33 |
| [16] | 安健, 刘好德, 滕靖, 等. 快速公交路径优化设计模型及算法研究[J]. 公路交通科技, 2010, 27(3): 147-153 AN Jian, LIU Hao-de, TENG Jing, et al. Research on Model and Algorithm of BRT Route Optimal Design[J]. Journal of Highway and Transportation Research and Development, 2010, 27(3): 147-153 |
| [17] | 税文兵, 叶怀珍, 张诗波. 考虑库存成本的配送中心动态选址模型及算法[J]. 公路交通科技, 2010, 27(4): 149-154 SHUI Wen-bing, YE Huai-zhen, ZHANG Shi-bo. A Dynamic Distribution Center Location Model and Algorithm with Inventory Cost[J]. Journal of Highway and Transportation Research and Development, 2010, 27(4): 149-154 |
| [18] | 吴小虎, 徐琪. 基于自适应网格粒子群算法的多目标配送优化模型[J]. 公路交通科技, 2010, 27(5): 132-136 WU Xiao-hu, XU Qi. Optimization Model of Multi-objective Distribution Based on Adaptive Grid Particle Swarm Optimization Algorithm[J]. Journal of Highway and Transportation Research and Development, 2010, 27(5): 132-136 |
 2017, Vol. 34
2017, Vol. 34
