扩展功能
文章信息
- 汪林
- WANG Lin
- 基于预测的快速公交信号优先设计及效果仿真
- Signal Priority Design for Bus Rapid Transit Based on Prediction Method and Effect Simulation
- 公路交通科技, 2017, 34(6): 129-135
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(6): 129-135
- 10.3969/j.issn.1002-0268.2017.06.019
-
文章历史
- 收稿日期: 2016-08-16
公交信号优先控制策略的研究主要经历了被动式、主动式和预测式3个阶段[1-2]。早期的被动式信号控制围绕单交叉口饱和度等影响因素建立优先控制模型,并辅以静态的干线协调控制手段[3-5]。而传统的主动信号优先控制主要以绿灯延长、红灯早断、相位插入等响应式方法,来获得合适的公交信号优先控制策略[6-9]。但上述方法因难以适应复杂的交通状况和优先突然性等原因,限制了公交优先的力度。部分学者通过GPS或AVL获得的实时数据,预测公交到达目标交叉口的行驶时间和站点停留情况,对公交车离站时间和发送信号优先请求时间进行调整,并按绿信比调整信号周期中各相位的长度,使公交车辆优先通过目标交叉口,主动信号优先的控制效率得到提高[10-12],但现有研究大多没有将干线联动的思路纳入预感应信号优先的考虑范畴。
预测式的公交信号优先依赖于良好的公交行程时间预测方法[13-15]。基于公交专用道行驶的车辆在路段上的行驶较为平稳,路段上的行程时间很容易得到,故预感应信号优先的核心就是较为准确且高效地预测公交车辆在站点的延误。从国内外学者的研究不难发现,短时延误预测具有相当的不确定性,这主要来自于真实世界庞大的非线性内在联系,以往的预测往往受制于数据量和计算速度之间的矛盾,只能采用运行较快、精度较低的近似线性模型进行预测。
文中采用自回归滑动求和平均(ARIMA)与支持向量机回归(SVR)进行组合预测,将车辆延误的时间序列看成由线性自相关和非线性结构两部分组成,分别采用相应方法预测叠加,获得良好的预测效果,并以此为依据,以预感应信号优先为基础,提出局部交叉口群之间的联动控制和信号优先力度约束条件,建立一套实用的快速公交(BRT)前提下的公交信号优先控制算法。
为了验证研究的正确性和有效性,选取某城市BRT线路作为实例,通过微观交通仿真软件VISSIM进行仿真,选取恰当的评价指标分析实例效果。
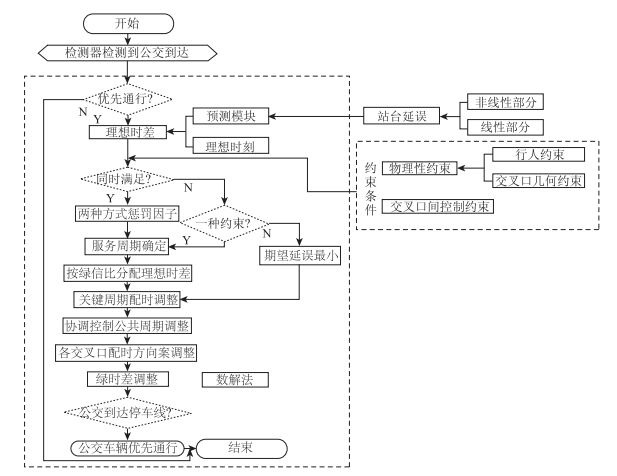
1 预感应公交信号优先干线联动控制算法 1.1 算法框架区别于传统的公交优先控制方法,改进的公交信号优先干线联动控制策略模型在公交车辆距离控制目标交叉口群较远处设置检测器,对公交到达关键交叉口时刻进行预测,根据预测时间和交叉口干线联动控制因素对信号优先控制方式进行选择,其理论流程如图 1所示。主要包括3个方面内容:关键交叉口信号周期绿灯时间调整算法、交叉口协同控制相位差计算方法、车辆到达时间预测模块。
|
| 图 1 预测式公交信号优先协同控制流程图 Fig. 1 Flowchart of predicted transit signal priority with coordinated control |
| |
1.2 确定关键信号周期
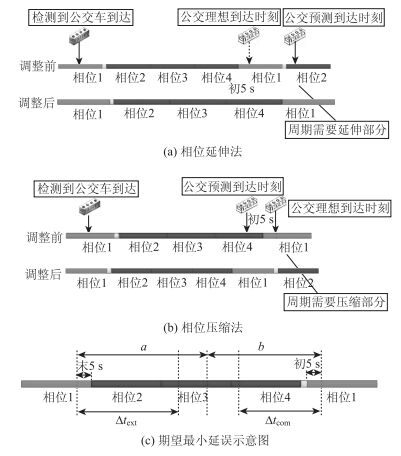
关键周期是关键交叉口的信号周期。根据提前检测公交到达关键交叉口的预测时间,判断公交车辆是否需要采取信号优先措施。若公交到达时刻位于公交服务相位的绿灯时间内,则关键周期的配时方案不变,否则,需要采取优先措施。优先调整措施分信号相位长度延伸和压缩两种,调整过程如图 2所示。
|
| 图 2 信号调整示意图 Fig. 2 Schematic diagram of signal adjustment |
| |
当公交车需要采取信号优先措施时,首先分别计算采用延伸和压缩两种相位调整方法的公交车预计到达目标交叉口停车线时刻与理想到达时刻(公交服务相位绿灯时间初5 s)的理想时间差Δt(Δtext为相位延伸方法的总调节量,Δtcom为相位压缩方法的总调节量)和两种调整方法的可调整周期数N,并判断两种方法调整后的周期长度是否满足周期约束条件。当两种方法的周期调整值均满足周期约束条件时,分别计算两种信号调节方式的惩罚因子P[12](延伸:P=Δtext+0.025Δtext2;压缩:P=Δtcom),相位延长比相位压缩对交叉口的通行能力影响更大,选择惩罚因子小的方法进行信号相位的调整;当只有一种方法的周期调整值满足周期约束条件时,选择该种调整方法进行信号相位的调整;当两种方法的周期调整值均不满足周期约束条件时,采用期望延误D最小的信号相位最大调整方案进行信号调整(a,b分别为相位延伸和相位压缩情况下,车辆预计到达时间与理想到达时间的时间差值,延伸:D=a-Δtext;压缩:b-Δtcom),如图 2(c)所示。
确定信号周期调整方法后,将理想时间差按各相位绿信比分配至各可调整周期的信号相位中:
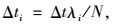
|
(1) |
式中,Δti为可调节周期第i相位的调节量;Δt为理想时间差;λi为主要周期第i相位绿信比;N为可以调整的周期数,可由式(2) 确定:
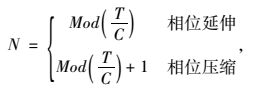
|
(2) |
式中,T为公交车到达目标交叉口的预测时间;C为交叉口协同控制的公共周期值。
当目标交叉口停车线前公交优先申请结束但检测器未检测到公交车到达时,交叉口信号配时方案在下个周期恢复初始设置,直至检测器再次检测到公交车到达。
1.3 协同控制因素约束分为行人约束、交叉口几何约束、信号协同控制约束,分别按以下方法计算。
1.3.1 行人约束根据上海市工程建设规范《城市道路平面交叉口规划与设计规程》,考虑行人过街所需最短绿灯时间gmin:
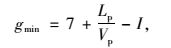
|
(3) |
式中,gmin为行人过街所需最短绿灯时间;Lp为行人过街横道长度;Vp为行人过街步速(可取1.2 m/s);I为绿灯时间间隔。
1.3.2 交叉口几何约束信号配时必须考虑交叉口几何条件约束,即在排队车道长度有限的情况下,确定相应的最大周期值,确保各相位的绿灯时间得到充分利用,以提高整个交叉口的运行效率。为使各相位的车流不发生排队溢出,交叉口的最大信号周期Cmax为:
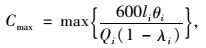
|
(4) |
式中,Cmax为交叉口配时最大信号周期值;li为各相位最大排队车道长度;Qi为各相位最大车道流量;λi为各相位绿信比;θi为各相位排队长度修正系数。
1.3.3 交叉口间协同控制因素在不破坏交叉口协同控制的基础上,保证公交车在交叉口间的系统怠速处于某较快的速度区间内,即保证公交在协同控制交叉口间的运行高效性和稳定性。同时,较快的怠速与路段社会车辆的行驶速度相近,这样交叉口间的协同绿波既能服务于公交车流也能服务于社会车流。交叉口间的协同控制约束条件为:

|
(5) |
式中,C为交叉口协同控制的公共周期值;s为理想信号位置间距值;v1和v2分别为公交车系统怠速区间的上限和下限。
定时式线控系统配时方案中绿时差的计算一般采用数解法(进行数解法计算的备选信号采用韦伯斯特算法),文中不再赘述,这里主要阐述改进数解法的不同之处。
与社会车流在两交叉口间路段无阻碍(不考虑交通流内部和其他外部因素的影响)不同,公交车需要进行进出站及停靠上下客,这使得两者在路段所需的行驶时间存在差异。文中将公交车在站点的停靠时间t转换为路段的空间距离s,路段修正空间距离L即为交叉口间的实际空间距离l与站点停靠延误转换空间距离s之和。根据修正后的路段空间距离L,采用干线绿波计算方法重新确定交叉口间的绿时差百分比,并根据实时调整的公共周期时长调整交叉口间协同控制的绿时差。
1.4 组合预测模型BRT停站时间的大小不仅拥有一定的线性纵向时间相关性,整个停靠过程又是公交车内部系统相互作用、公交车与乘客作用、公交车与行驶自然环境作用的综合结果,存在一定的非线性。由于BRT停站过程存在着线性和非线性的双重特性,本研究采用组合模型式方法对BRT的停站时间进行预测,将快速公交站点的停靠时间分为线性自相关部分与非线性部分,这两部分分别对应考虑停靠时间的时间纵向相关性和物理作用的模糊过程。在具体方法上,ARIMA方法[16]是较为常用的线性时间序列预测方法,支持向量机(SVR)[17-18]方法则常被使用在非线性回归当中,用ARIMA方法预测停靠时间的第1部分,即线性自相关部分,而另一部分则用非线性预测方法——SVR进行预测,并将两部分结果进行叠加,得出最终预测结果。
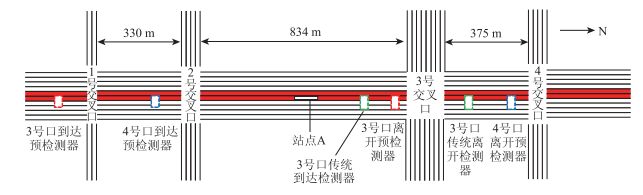
2 实例验证文中以某城市BRT线路部分路段为实例,以验证文中控制方法的有效性和正确性。本研究区段途经公交线路及其支线共3条,流量为115 veh/h。在晚高峰时段,存在明显潮汐现象,本次公交信号优先控制检测器均由南向北布设,涉及预测的公交站为站点A,如图 3所示。
|
| 图 3 某市BRT研究区段信息示意图 Fig. 3 Schematic diagram of information of BRTs study region in a certain city |
| |
2.1 预测模型结果
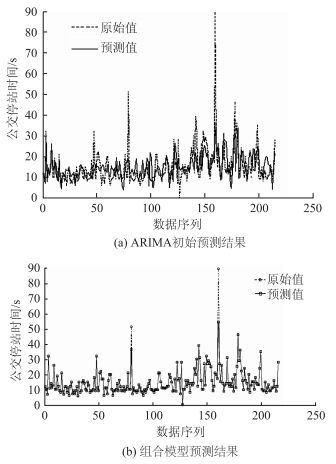
根据站点A采集得到的214个公交停站时间数据,按照其到站时刻由小到大排列,可以组成1组停站时间序列。首先,运用ARIMA算法对停站时间的线性部分进行预测,采用网格法搜索模型的p, q, d参数,计算AIC统计量最优的参数组合作为预测参数,通过观察序列的自相关函数和偏相关函数图,p和q均初定为0~20,d初定为0~2。通过matlab编码得到模型参数d=0,p=4,q=20,预测第1步结果如图 4(a)所示。
|
| 图 4 停站时间预测效果 Fig. 4 Effect of dwell time prediction |
| |
不难看出,线性预测虽然能表征停站时间的大致分布趋势,却不能精确刻画BRT车辆的停站时间,这是不符合预感应信号控制要求的,因此构造SVR预测方法所需向量,将BRT车辆的到站时间、瞬时社会车辆流率以及BRT车辆到站时间间隔作为单个向量的3个因子,将214个向量输入SVR预测模块,得到BRT车辆停站时间的非线性部分,并与第1步所得结果进行叠加,预测结果如图 4(b)所示。
完成组合预测过程后,对原始数据和预测结果数据进行统计,可以得到均方误差MSE和相关系数R两项指标:MSE=6.803 6,R=0.890 4。预测结果的均方误差较小,相关系数较为接近1。由此可见组合模型可以较为精准地预测短时交通流的延误值,为预感应公交信号优先奠定了良好的技术基础。
2.2 车辆仿真环境与评价研究区域的主要交叉口为3号交叉口,协同控制分析路口为4号交叉口。仿真情景设置为原始情况、传统感应信号优先和基于停站时间预测的预测式优先。仿真时段为该区段晚高峰(17:00—19:00),交叉口流量如表 1所示。对于公交运行效益而言,主要采用延误和车头时距一致性两个典型指标分析,而社会车辆则采用延误和排队长度分析其受到公交优先的影响。
| 交叉口 序号 | 东进口 | 西进口 | 南进口 | 北进口 | ||||||||
| 左转 | 直行 | 右转 | 左转 | 直行 | 右转 | 左转 | 直行 | 右转 | 左转 | 直行 | 右转 | |
| 1 | 0 | 20 | 24 | 56 | 0 | 84 | 112 | 1 128 | 0 | 64 | 1 328 | 324 |
| 2 | — | — | — | 160 | 12 | 20 | 36 | 1 080 | 42 | 232 | 1 364 | 120 |
| 3 | 258 | 610 | 310 | 102 | 1 042 | 666 | 250 | 780 | 206 | 374 | 1 144 | 108 |
| 4 | 68 | 100 | 84 | 106 | 64 | 44 | 104 | 968 | 110 | 66 | 1 328 | 232 |
2.2.1 仿真情景
(1) 原始情况
本次研究区域中的各个交叉口没有针对BRT设置公交信号优先措施,交叉口间也没有设置协同控制。该模式即是现状控制方式的微观仿真模式,用来分析其他两种信号优先方法对现状交通运行的影响。
(2) 传统感应信号优先
本次传统信号优先方法的具体设置是:在公交专用道进口道停车线前20 m处设置检测器,当有公交车到达时,首先判断该辆公交车到达交叉口时公交服务相位是否为绿灯,若无法绿灯通过,则将公交服务相位绿灯时间延长10 s,反之,信号不变。该模式的设置主要用来与预感应信号优先控制方法进行比较,分析它与预感应信号方式的优劣及对其他交通方式的影响。
(3) 基于预测的信号协同优先
基于预测的信号协同优先即是本次研究的公交信号优先控制方法。本次研究的方法在公交高峰的基础上提出了更加明确的信号周期约束条件,并考虑交叉口间的协同控制因素。该模式的设置主要用于分析本次理论研究的BRT信号优先控制方法的实例实施效果。
2.2.2 评价分析(1) 公交评价
公交干线的延误多集中在交叉口,且公交按一定的时间间隔发车。公交到站越规律,说明信号优先的效果越好,因此,公交评价指标选取公交交叉口延误和公交车头时距一致性两项。
表 2显示了传统公交信号优先和基于组合预测的信号优先相比于无信号优先的公交车在交叉口延误的降低情况,其中在关键交叉口(3号交叉口)两种方式分别降低了2.1 s和8.8 s,而在次要交叉口(4号交叉口),预感应信号式优先骤降15.2 s,但传统式优先却增加了延误,其原因是高峰时段公交车优先申请频繁,传统方法没有很好地处理好申请冲突,且交叉口距离较近时没有采取协同控制模式。至此不难看出,良好的预测方法和预感应信号优先法的理念对公交优先的贡献着实不小。与延误类似,公交车到站一致性在传统信号优先和预感应信号优先的策略下都有所降低,公交到站更均匀,服务水平更高。
| 仿真情景 | 公交平均延误 | 车头时距一致性 | |||||
| 3号 交叉口/s | 下降/ % | 4号 交叉口/s | 下降/ % | BRT1 路 | BRT11 路 | BRT12 路 | |
| 现状 | 17.6 | 0 | 18 | 0 | 0.139 | 0.233 | 0.128 |
| 传统优先 | 15.5 | 11.9 | 18.7 | -3.9 | 0.114 | 0.233 | 0.126 |
| 预测式算法 | 8.8 | 35.3 | 2.8 | 77.0 | 0.086 | 0.138 | 0.080 |
综上所述,在良好的预测前提下,加入协同控制的公交信号优先策略表现更为突出,3条公交线的车头时距一致性平均降38.8%。
(2) 社会车流评价
私家车等社会车辆是城市道路交通的主要组成部分。在优先发展城市公共交通的同时,合理处理好公交与社会车辆之间的关系变得十分重要。社会车辆的评价指标主要是社会车流的交叉口延误及交叉口处的排队情况,见表 3。
| 仿真情景 | 平均延误/s | 排队总长m | ||
| 3号交叉口 | 4号交叉口 | 3号交叉口 | 4号交叉口 | |
| 现状 | 41.2 | 16.3 | 264 | 102 |
| 传统优先 | 60.8 | 16.3 | 411 | 104 |
| 预感应算法 | 46.6 | 16.2 | 299 | 106 |
总体来看,无论是何种优先方法,都会在一定程度上对社会车流的通行造成巨大影响。传统信号优先对于社会车流的影响较大:累计延误与现状相比增加34.1%,而预测式信号优先算法的影响最小:延误仅增加了现状的9.2%,这是由于较快的公交怠速与社会车流速度相近,使得部分社会车流受益于交叉口间的协同控制作用。
社会车流的排队总长度在一定程度上也证明了不同公交优先方式在高峰期对社会车流影响是:传统信号优先>预测式信号优先。
2.3 仿真结果总结综上所述,相比于现状和传统优先方法,预测式信号优先方式能够显著降低公交交叉口的延误和提高公交服务可靠性,同时对社会车流的干扰更小。3种情况模拟仿真的对比评价结果显示,预感应信号优先方法获得的系统效果最佳,充分证实了该种方法的有效性和实用价值。
3 结论本研究在借鉴预感应信号控制的基础上对算法进行了改进,运用以ARIMA-SVR的组合预测算法为基准、以交叉口群协同控制为指导、以各项约束控制优先为准则的适用于快速公交情况下的预测式信号优先算法,并结合BRT工程实例,借助VISSIM仿真,证明了预测式信号优先算法的优越性,研究结论如下:
(1) 以预测式公交信号优先控制理论为基础,以快速公交为研究条件,提出了减少公交干线交叉口公交延误的带有条件约束的关键交叉口信号调整算法和干线交叉口的干线联动控制算法。
(2) 以工程实际的BRT停靠站数据为支撑,运用组合预测模型,较好地预测了公交站台停留数据,为预测式信号控制方法提供了参数支撑。
在本研究的基础上,将在公交优先面控、信号优先后的配时恢复及信号优先触发条件的参数量化等方面进一步深入研究。
| [1] | CHANG J, COLLURA J, DION F, et al. Evaluation of Service Reliability Impacts of Traffic Signal Priority Strategies for Bus Transit[J]. Transportation Research Record, 2003, 1841: 23-31 |
| [2] | MA W J, XIE H Z, BAI Y, et al. Signal Timing Optimization Model Based on Dual-ring Phase Scheme for Roundabout[J]. Journal of Central South University, 2013, 20(2): 563-571 |
| [3] | YAGAR S, CASE E R. A Role for VNIS in Real-time Control of Signalized Networks? [C]//Vehicle Navigation and Information Systems Conference. New York: IEEE, 1991:1105-1109. |
| [4] | 马万经, 吴志周, 杨晓光. 基于交叉口群公交优先协调控制方法研究[J]. 土木工程学报, 2009, 42(2): 105-111 MA Wan-jing, WU Zhi-zhou, YANG Xiao-guang. A Coordinated Intersection-group Bus Signal Priority Control Approach[J]. China Civil Engineering Journal, 2009, 42(2): 105-111 |
| [5] | 李林, 徐建闽, 卢凯. 干道交通协调控制的MILP改进算法[J]. 公路交通科技, 2009, 26(增2): 93-96 LI Lin, XU Jian-min, LU Kai. An Improved Algorithm for Arterial Traffic Coordinated Control Based on Mixed Integer Linear Programming[J]. Journal of Highway and Transportation Research and Development, 2009, 26(S1): 93-96 |
| [6] | 杨晓光, 林瑜, 杭明升. 信号控制交叉口公共汽车优先信号确定方法研究[J]. 中国公路学报, 2001, 14(增2): 101-104 |
| [7] | EKEILA W, SAYED T A, ESAWEY M E. Development of Dynamic Transit Signal Priority Strategy[J]. Transportation Research Record, 2009, 2111: 1-9 |
| [8] | TAN C W, PARK S, LIU H, et al. Prediction of Transit Vehicle Arrival Time for Signal Priority Control: Algorithm and Performance[J]. IEEE Transactions on Intelligent Transportation Systems, 2008, 9(4): 688-696 |
| [9] | SKABARDONIS A. Control Strategies for Transit Priority[J]. Transportation Research Record Journal of the Transportation Research Board, 2000, 1727: 30-34 |
| [10] | KIM W, RILETT L. An Improved Bus Signal Priority System for Networks with Nearside Bus Stops[J]. Transportation Research Record, 2005, 1925: 205-214 |
| [11] | 郭欣蕾, 张海. BRT线路公交信号优先协调与控制方法研究[J]. 交通运输系统工程与信息, 2009, 9(3): 128-134 GUO Xin-lei, ZHANG Hai. Traffic Signal Priority and Control Method of BRT[J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(3): 128-134 |
| [12] | 高歌, 高克. BRT信号优先系统控制与设计[J]. 交通科技与经济, 2011, 13(1): 47-50 GAO Ge, GAO Ke. Design on Traffic Signal Control for BRT's Priority[J]. Technology & Economy in Areas of Communications, 2011, 13(1): 47-50 |
| [13] | WADJAS Y, FURTH P G. Transit Signal Priority Along Arterials Using Advanced Detection[J]. Transportation Research Record, 2003, 1856: 220-230 |
| [14] | DING J, YANG M, WANG W, et al. Strategy for Multiobjective Transit Signal Priority with Prediction of Bus Dwell Time at Stops[J]. Transportation Research Record, 2015, 2488: 10-19 |
| [15] | 何兆成, 招玉华, 赵建明, 等. 基于状态判别的单点交叉口信号配时优化方法[J]. 公路交通科技, 2010, 27(7): 100-104 HE Zhao-cheng, ZHAO Yu-hua, ZHAO Jian-ming, et al. A Signal Timing Optimization Method for Isolated Intersection Based on Traffic Status Identification[J]. Journal of Highway and Transportation Research and Development, 2010, 27(7): 100-104 |
| [16] | 谭满春, 冯荦斌, 徐建闽. 基于ARIMA与人工神经网络组合模型的交通流预测[J]. 中国公路学报, 2007, 20(4): 118-121 TAN Man-chun, FENG Luo-bin, XU Jian-min. Traffic Flow Prediction Based on Hybrid ARIMA and ANN Model[J]. China Journal of Highway and Transport, 2007, 20(4): 118-121 |
| [17] | 陆海亭. 基于SARIMA和SVM模型的短时交通流预测[D]. 南京: 东南大学, 2010. LU Hai-ting. Short Term Traffic Flow Forecast Based on SARIMA and SVM Models [D]. Nanjing: Southeast University, 2010. |
| [18] | 杨敏, 丁剑, 王炜. 基于ARIMA-SVM模型的快速公交停站时间组合预测方法[J]. 东南大学学报:自然科学版, 2016, 46(3): 651-656 YANG Min, DING Jian, WANG Wei. Hybrid Dwell Time Prediction Method for Bus Rapid Transit Based on ARIMA-SVM Model[J]. Journal of Southeast University: Natural Science Edition, 2016, 46(3): 651-656 |
 2017, Vol. 34
2017, Vol. 34
