扩展功能
文章信息
- 姜彦宁, 徐奇, 任晗, 靳志宏
- JIANG Yan-ning, XU Qi, REN Han, JIN Zhi-hong
- 资源共享模式下的整车物流路径优化
- Automobile Logistics Routing Problem Optimization under Resource Sharing Mode
- 公路交通科技, 2017, 34(6): 114-121
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(6): 114-121
- 10.3969/j.issn.1002-0268.2017.06.017
-
文章历史
- 收稿日期: 2015-04-07
2. 交通运输部, 北京 100736;
3. 大连海事大学 综合交通运输协同创新中心, 辽宁 大连 116026
2. Ministry of Transport, Beijing 100736, China;
3. Collaborative Innovation Center for Transport Studies, Dalian Maritime University, Dalian Liaoning 116026, China
我国汽车市场正逐渐成为全球最大的汽车产销市场。汽车产销量的急剧攀升,对整车物流的规模和服务水平提出了更高的要求。整车物流路径优化是提高企业运作效率,进而扩大物流规模、提升服务水平的有效手段。此外,整车物流势必向集约化的方向发展,以物流联盟的形式,在资源共享模式下的物流运作是整车物流企业提升其竞争力的必然选择。
关于整车物流的研究,吴保峰等[1]对我国整车物流发展现状及趋势进行了分析,并指出整车物流资源整合是有效的发展途径;张雪婷等[2]基于逐层递进的方法,对考虑不同规格条件下的整车物流规划问题进行了分析;V. Pillac[3]基于事件驱动框架对变化进行预估,求解了动态随机需求条件下的车辆约束问题;马士华等[4]考虑整车运输能力约束情况下同一承运车型的准时配载计划问题;秦绪伟等[5]构建了整车物流网络规划数学模型,并采用混合粒子群算法进行了求解;孙宝凤等[6]对信息对称与不对称条件下星形整车物流联盟的收益分配问题进行了研究;王婷[7]对返程带货条件下的整车汽车物流共同配送模式进行设计,并进行了仿真运行求解;张磊等[8]对汽车整车配载与运输路线优化问题共同进行了求解;S. Ceschia[9]构建了带时间窗的异构车辆路径优化模型,并设计了禁忌搜索算法对其进行求解;戢晓峰等[10]构建了交通管制时限条件下的城市物流配送优化双层规划数学模型,并设计了遗传算法求解该问题;钱丹等[11]对多车型联运整车物流配送优化问题进行建模,并设计了基于改进分支定界的新启发式优化算法;侯玉梅等[12]对带软时间窗约束的整车物流车辆路径问题进行建模,并设计了自适应遗传算法对其进行求解;熊军军[13]设计了基于贪婪算法和禁忌搜索的算法求解乘用车运输计划问题;钱丹等[14]建立了多承运车型联运的整车物流配送优化模型,并设计了基于改进分支定界的新启发式配载优化算法进行求解。李金夫等[15]构建了整车物流车辆路径优化数学模型,用以设计最优的车辆物流装载方案和运输计划,并设计了贪心算法和遗传算法相结合的混合算法进行仿真求解;张远[16]构建了多轿运车、多乘用车的整车物流模型,并设计了改进模拟退火算法求解问题;窦莉薇[17]设计了改进蚁群算法用于求解整车物流多式联运路径问题;齐心[18]建立了物流配送路径优化模型,并设计了基于遗传算法和模拟退火算法的综合启发式算法。
对已有研究的分析表明,整车物流路径优化是提高运作效率的有效方式,已获得众多学者的公认,并对该问题展开了研究。但对资源共享下的整车物流路径优化这一研究方向仍有待进一步探索。文中对资源共享模式下的整车物流路径优化问题进行分析,构建以物流网络总成本最小为目标的数学优化模型,并设计启发式算法用于求解该问题。结合华晨宝马、上海通用及广州本田的整车物流运输实例对所构建的模型及算法进行验证。
1 整车物流资源共享模式通过对整车物流资源进行共享,可以对该行业的资源进行整合,进而扩大整车物流规模和提高服务水平。文中提出的整车物流资源共享模式包括共享车辆与共享VDC(车辆分拨中心)两种。
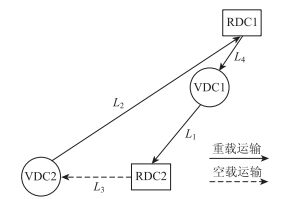
1.1 共享车辆模式在非共享车辆模式下,各企业均需独立执行VDC至RDC(区域分拨中心)的整车运输,此模式下必然造成承担运输任务的车辆在完成从VDC重载到达RDC后,空载返回至VDC的情况。而在共享车辆的模式下,可有效地减少运输车辆的空载行驶。以图 1为例进行说明,在共享车辆模式下,运输车辆从VDC1重载驶至RDC2后,空载驶至VDC2,之后再从VDC2重载驶至RDC2,空载返回VDC1。可知该模式下的运输总距离为L1+L2+L3+L4。而在非共享模式下,由于存在分属两个不同公司的分拨中心(VDC1,RDC1;VDC2,RDC2),运输总距离为2(L1+L2)。则在共享车辆模式下节省的运输距离为L1+L2-L3-L4,且L1+L2比L3+L4大得越多,节省运输距离的幅度越明显。
|
| 图 1 共享车辆模式图示 Fig. 1 Illustration of vehicle sharing mode |
| |
1.2 共享VDC模式
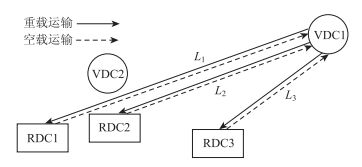
假设在非共享VDC模式下,有VDC1到RDC1,RDC2,RDC3诸个节点的运输需求,此时整车物流的运输距离2(L1+L2+L3),如图 2所示。
|
| 图 2 非共享VDC模式图示 Fig. 2 Illustration of non VDC sharing mode |
| |
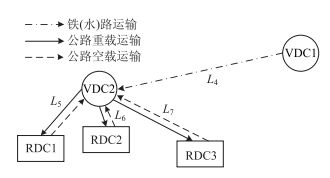
而在共享VDC模式下,由于VDC2距RDC1,RDC2,RDC3较近,因此可考虑先通过批量运输由VDC1集中到VDC2,再经由VDC2重载运输至各RDC,再空载返回至VDC2,如图 3所示。在该模式下,运输总距离为L4+2(L5+L6+L7),较非共享模式节约的里程为2(L1+L2+L3-L5-L6-L7)-L4。此外,由于VDC1到VDC2之间的运量比直接运至RDC的运量大,可考虑使用铁路(或水路)运输,更能节约运输成本。
|
| 图 3 共享VDC模式图示 Fig. 3 Illustration of VDC sharing mode |
| |
上述两种模式都是在不重新规划VDC及RDC选址的前提下所建议采用的资源共享模式,可为企业提供过渡性的运作策略,其运营成本将远低于传统模式下的运营成本。
2 整车物流路径优化模型构建 2.1 假设条件与符号定义(1) 构建整车物流路径优化模型所提出的假设条件
① 使用铁路(或水路)方式进行整车运输需要满足该种运输方式的最小运量需求。
② VDC规模较大,可满足各RDC的需求。
(2) 符号定义
① 参数
V为参与资源共享的整车物流企业VDC的集合;
R为参与资源共享的整车物流企业RDC的集合;
i, i′分别为RDC的标号;
j, j′分别为VDC的标号;
dij 为VDC i与RDC j之间的距离;
dij为VDC i与VDC j之间的距离;
dij′为RDC i与VDC j′之间的距离;
djj′为VDC j与VDC j′之间的距离;
cl为公路重载运输方式下的单位运输成本;
c为公路空载运输方式下的单位运输成本;
cs为水路运输方式下的单位运输成本;
cr为铁路运输方式下的单位运输成本;
qij为RDC i从VDC j调运整车的需求量,若无需求则qij=0;
Qs为水路运输要求满足的最小运量;
Qr为铁路运输要求满足的最小运量;
lj′为VDC j′所处的位置类型,lj′=0时表示VDC j′是内陆城市,lj′=1时则表示VDC j′是沿海城市。
② 变量

|
构建以参与资源共享模式企业的整车运输总成本最小为目标函数的路径优化数学模型如下。
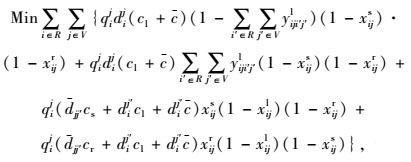
|
(1) |
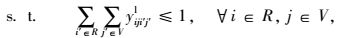
|
(2) |
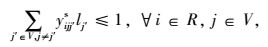
|
(3) |
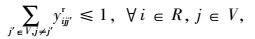
|
(4) |
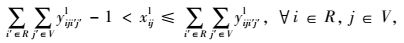
|
(5) |
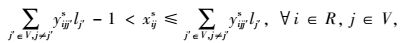
|
(6) |
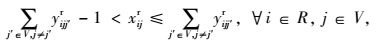
|
(7) |
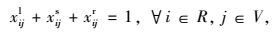
|
(8) |
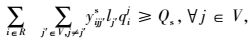
|
(9) |
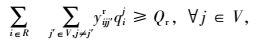
|
(10) |
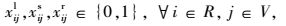
|
(11) |
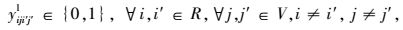
|
(12) |
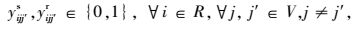
|
(13) |
式(1) 为共享模式下的总运输成本,具体包括传统模式下的运输成本、共享车辆模式下的运输成本、采用水路运输方式的运输成本以及采用铁路运输方式两类共享VDC模式下的运输成本之和。式(2) 表示RDC i对VDC j之间的需求只能选择1个运输流进行共享车辆运输。式(3)~(4) 分别表示两个VDC间采用水路运输/铁路运输时,RDC i最多只能经1个VDC中转用以满足对VDC j的需求。式(5) 是对决策变量xijl的定义公式,具体为:如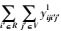
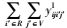
前文所构建的路径优化模型涉及变量较多,且目标函数为非线性,使用精确解算法求解难度较高。遗传算法已被广泛应用于求解车辆路径优化问题,并取得了较好的效果。由于文中所提出的问题属于一类联运模式下的车辆路径优化问题,基于经典遗传算法进行改进,设计基于遗传算法的启发式算法,用以求解所构建模型,以获得近似最优解。
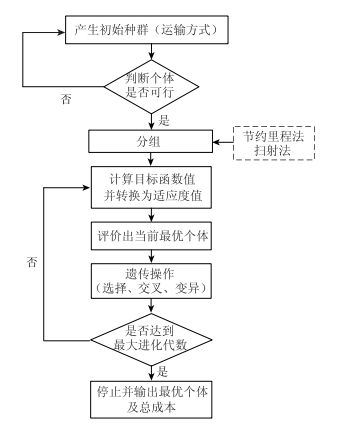
3.1 算法框架采用先确定运输方式后进行分组的算法模式。其核心思想是:先确定各运输流的运输方式,之后再为每条运输流进行配对,选择合适的运输流。在运输方式确定阶段,应用遗传算法操作算子生成运输方式;在分组阶段,则基于不同的运输方式,选择使用节约里程法及扫描法进行运输流的整合。以此进行不断的进化迭代,最终获得近似最优解。算法流程图如图 4所示。
|
| 图 4 基于遗传算法的启发式算法流程图 Fig. 4 Flowchart of heuristic algorithm based on genetic algorithm |
| |
3.2 染色体的表示与初始种群的生成
(1) 染色体的表示形式
根据问题特征,文中采用整数编码的方式表示染色体。染色体的长度为运输流的个数,基因值可取1,2,3,4,用来表示4种运输模式,具体包括:传统运输模式、共享车辆模式、经水路中转共享VDC模式、经铁路中转共享VDC模式。以图 5为例进行说明:假设整车物流网络中包含4个VDC(前两个位于沿海,后两个位于内陆)、9个RDC、20条运输流,则该例中的基因长为20。基因1~5,6~10,11~14,15~20分别代表从VDC1,VDC2,VDC3,VDC4出发的运输流所采用运输模式。例如,从VDC1到RDC1,RDC3,RDC 4,RDC 5,RDC 7所采用的运输模式分别为:传统运输模式、经水路中转共享VDC、共享车辆、经铁路中转共享VDC、传统运输模式。

|
| 图 5 染色体图示 Fig. 5 Illustration of chromosome |
| |
(2) 初始种群的生成
以随机方式生成初始种群,作为遗传算法迭代的初始点。但由于内陆城市不能采用经水路中转共享VDC模式,因此在生成的过程中需要对部分基因值进行修改,具体方法是:如VDC所在位置为内陆城市,判断从该VDC出发的运输流所对应的基因值是否为3,如是,则重新生成其他基因值。
3.3 基于节约里程法及扫描法的分组操作初始种群产生后,除传统运输模式外,对其他的运输流需要进行分组操作。如基因值为1,则不需要进行分组;如基因值为2,则用节约里程法进行整合;如基因值为3或4,则用扫描法进行整合,并选择中转VDC。
(1) 基于节约里程法的分组操作
Step 1:对于任意两条基因值为2的运输流对(i,j),计算其节约值Sij。
Step 2:对所有节约值进行降序排列,进而获得运输流对顺序集合{S}。
Step 3:重复以下步骤,直到{S}=φ。
Step 3.1:基于{S}中的顺序,对运输流对(i,j)进行整合,即这两条运输流采用共享车辆模式。
Step 3.2:在{S}中删除所有与i,j相的节约值,并更新{S}。
Step 4:如仍剩余基因值为2的运输流,则修改其基因值为1。
(2) 基于扫描法的分组操作
Step 1:随机选择1个VDC为旋转中心。
Step 2:选择基因值为3,且未设为旋转中心的VDC k。令i=1。
Step 3:从所有未被分组的RDC中,选择最小角度的RDC分配至第i组。如超过容量限制,则i=i+1。重复此步骤,直到从VDC k出发的所有基因值为3的运输流都已被扫描。
Step 4:对于被整合到1组的RDC,计算从VDC k经各VDC中转完成该组需求的运输成本,选择最小运输成本所对应的VDC j 作为该组RDC的中转VDC。
Step 5:重复前述步骤,直到所有基因值为3的运输流都完成整合。
3.4 遗传操作(1) 选择操作
采用轮盘赌算子进行选择操作。具体过程为旋转轮盘若干次,每次选出1个个体作为新种群的成员。设种群数为N,个体i和k的适应度分别定义为fi和fk,则个体i被选取的概率为Pi=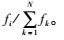
(2) 交叉操作
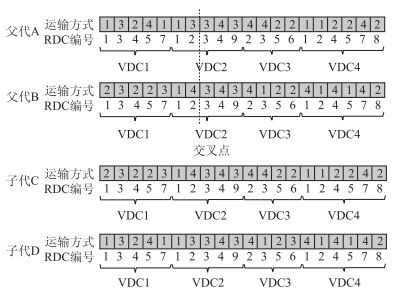
采用单点交叉算子进行交叉操作。对两个父代染色体,随机产生1个交叉点,将交叉点左侧的基因进行互换,形成两个子代染色体,如图 6所示。
|
| 图 6 交叉操作示图示 Fig. 6 Illustration of crossover operation |
| |
(3) 变异操作
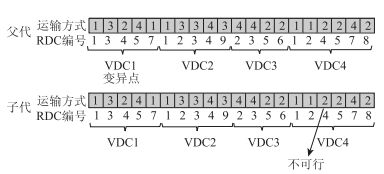
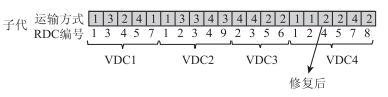
采用基本位变异算子执行变异操作。具体对染色体的各个基因座按照变异概率重新生成该基因座的基因值。变异操作如图 7所示。由于采用经水路中转共享VDC模式对VDC存在地理位置限制,因此在变异操作后可能导致不可行个体的产生,需要进行基因修复。具体修复方法是:对于从内陆城市在VDC出发且基因值为3的运输流,随机生成基因值1,2或4,替换原有基因值。基因修复过程见图 8。
|
| 图 7 变异操作图示 Fig. 7 Illustration of mutation operation |
| |
|
| 图 8 基因修复操作图示 Fig. 8 Illustration of gene repair operation |
| |
4 案例求解与分析 4.1 案例数据
以华晨宝马、上海通用、东风日产3家汽车公司为例进行实例分析。3家公司VDC与RDC的分布情况等相关数据如表 1~表 4所示。
| 企业 | VDC位置 | RDC位置 |
| 华晨宝马 | 沈阳(1) | 北京(1)、上海(2)、福清(3)、成都(4)、广州(5) |
| 上海通用 | 上海(2) | 天津(6)、咸阳(7)、德阳(8)、广州、东莞(9)、昆明(10) |
| 东风日产 | 广州(3) | 天津、大连(11)、沈阳(12)、北京 |
| VDC | RDC | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 664 | 1 581 | 2 420 | 2 263 | 2 691 | 619 | 1 656 | 2 173 | 2 357 | 2 778 | 367 | 0 |
| 2 | 1 177 | 0 | 664 | 1 771 | 1 312 | 975 | 1 315 | 1 745 | 1 286 | 2 081 | 1 758 | 1 581 |
| 3 | 1 959 | 1 312 | 782 | 1 320 | 0 | 1 929 | 14 23 | 1 348 | 56 | 1 178 | 2 627 | 2 691 |
| VDC | RDC | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 1.4 | 2.7 | 2.8 | 2.2 | 1.7 | — | — | — | — | — | — | — |
| 2 | — | — | — | — | 2.8 | 2.7 | 1.9 | 1.8 | 2.8 | 1.5 | — | — |
| 3 | 2.6 | — | — | — | — | 1.6 | — | — | — | — | 2.3 | 2.4 |
| VDC | 1沈阳 | 2上海 | 3广州 |
| 1沈阳 | 0 | 1 581 | 2 691 |
| 2上海 | 1 581 | 0 | 1 312 |
| 3广州 | 2 691 | 1 312 | 0 |
设置其余案例参数为:公路重载/空载运输方式下的单位运输成本分别为:cl=0.4元/(km·veh),c=0.3元/(km·veh);水路运输方式下的单位运输成本为:cs=0.2元/(km·veh);铁路运输方式下的单位运输成本为:cr=0.24元/(km·veh);水路/铁路运输要求满足的最小运量分别为:Qs=500,Qr=290。
4.2 案例求解与结果分析基于前述设计的启发式算法,采用C语言开发程序,并通过大量试验确定相关参数,设定种群规模为100,迭代代数为500,交叉与变异概率分别为0.8和0.1。对前述案例进行求解,求解结果如表 5所示。将该结果与传统运输方式的运输成本进行对比,如表 6所示。可以看出,在使用资源共享运输模式下,3家企业节省成本分别为26.74%,33.33%,30.62%,而总成本节约值则为30.08%。由此可知,基于本文所提出的资源共享运输模式可以有效地降低运输成本,提高运营绩效。
| 企业 | 运输流 | 运输方式与路线 | 每条运输流 成本/元 | 各企业总 成本/万元 |
| 华晨宝马 | 沈阳—北京 | 传统重去空回 | 65 072 | 110.40 |
| 沈阳—上海 | 共享运输车辆(沈阳—上海—天津) | 170 748 | ||
| 沈阳—福清 | 共享运输车辆(沈阳—福清—广州—大连) | 336 728 | ||
| 沈阳—成都 | 传统重去空回 | 348 502 | ||
| 沈阳—广州 | 共享运输车辆(沈阳—广州—沈阳) | 182 988 | ||
| 上海通用 | 上海—天津 | 共享运输车辆(沈阳—上海—天津) | 155 439 | 87.12 |
| 上海—咸阳 | 传统重去空回 | 174 895 | ||
| 上海—德阳 | 传统重去空回 | 219 870 | ||
| 上海—广州 | 经水路中转共享 VDC 3 | 320 970 | ||
| 上海—东莞 | ||||
| 上海—昆明 | ||||
| 东风日产 | 广州—天津 | 经铁路中转共享 VDC 2 | 455 663.6 | 98.10 |
| 广州—北京 | ||||
| 广州—沈阳 | 共享运输车辆(沈阳—广州—沈阳) | 258 336 | ||
| 广州—大连 | 共享运输车辆(沈阳—福清—广州—大连) | 267 007 |
| 企业 | 运输流 | 运输流成本/元 | 各运输流成本 节省率/% | 各企业总成本/万元 | 各企业总成本 节约率/% | ||
| 单独运输 | 共享运输 | 单独运输 | 共享运输 | ||||
| 华晨宝马 | 沈阳—北京 | 65 072 | 65 072 | 0 | 150.69 | 110.40 | 26.74 |
| 沈阳—上海 | 298 809 | 170 748 | 42.86 | ||||
| 沈阳—福清 | 474 320 | 336 728 | 29.01 | ||||
| 沈阳—成都 | 348 502 | 348 502 | 0 | ||||
| 沈阳—广州 | 320 229 | 182 988 | 42.86 | ||||
| 上海通用 | 上海—天津 | 184 275 | 155 439 | 15.65 | 130.68 | 87.12 | 33.33 |
| 上海—咸阳 | 174 895 | 174 895 | 0 | ||||
| 上海—德阳 | 219 870 | 219 870 | 0 | ||||
| 上海—广州 | 257 152 | 320 970 | 55.89 | ||||
| 上海—东莞 | 252 056 | ||||||
| 上海—昆明 | 218 505 | ||||||
| 东风日产 | 广州—天津 | 216 048 | 455 663.6 | 20.42 | 141.40 | 98.10 | 30.62 |
| 广州—北京 | 356 538 | ||||||
| 广州—沈阳 | 418 488 | 258 336 | 38.27 | ||||
| 广州—大连 | 422 947 | 267 007 | 36.87 | ||||
| 合计 | 4 227 706 | 2 956 218.6 | 30.08 | 422.77 | 295.62 | 30.08 | |
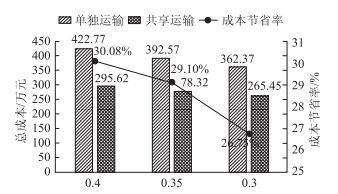
此外,公路重载运输方式下的单位运输成本调整后对最优成本的影响情况如图 9所示。
|
| 图 9 不同公路重载单位运输成本下最优成本的比较分析 Fig. 9 Comparison between optimal costs with different loaded road transport rates |
| |
从图 9可以看出,公路重载运输单位运输成本下降后,单独运输与共享运输模式下的总成本都存在一定幅度的下降。原因是单位运输成本越大,采用传统单独运输的成本越大,越应采用共享运输模式。但若公路重载运输单位成本与铁路和水路运输的成本越接近,则共享模式的优势越弱,成本节省率也就越低。
5 结论文中提出了资源共享模式下的整车物流路径优化问题,并构建了以参与资源共享模式企业的整车运输总成本最小为目标函数的路径优化数学模型。设计了基于遗传算法的启发式算法用于求解该问题,结合整车物流运输实例结果,认为资源共享模式可以比传统模式节约成本30%左右。对公路重载运输单位运输成本对最优成本的影响进行了比较分析。
| [1] | 吴保峰, 刘仲英. 我国整车物流发展趋势及资源整合问题研究[J]. 汽车工程, 2005, 27(3): 367-371 WU Bao-feng, LIU Zhong-ying. A Study on Finished Vehicle Logistics in China: Its Development Trend and Resource Integration[J]. Automotive Engineering, 2005, 27(3): 367-371 |
| [2] | 张雪婷, 陈英武, 王琦, 等. 整车物流的任务规划模型和算法[J]. 中国管理科学, 2015, 23(增2): 624-629 ZHANG Xue-ting, CHEN Ying-wu, WANG Qi, et al. Planning Model and Algorithm for Finished Vehicle Logistics[J]. Chinese Journal of Management Science, 2015, 23(S1): 624-629 |
| [3] | PILLAC V, GUERET C, MEDAGLIA A L. An Event-driven Optimization Framework for Dynamic Vehicle Routing[J]. Decision Support Systems, 2012, 54(1): 414-423 |
| [4] | 马士华, 张晓龙. 基于物流能力约束的整车物流计划[J]. 工业工程与管理, 2006, 11(6): 15-18, 32 MA Shi-hua, ZHANG Xiao-long. On Distribution Scheduling of Auto-logistics Based on Logistics Capability[J]. Industrial Engineering and Management, 2006, 11(6): 15-18, 32 |
| [5] | 秦绪伟, 范玉顺, 尹朝万. 整车物流网络规划问题的混合粒子群算法研究[J]. 系统工程理论与实践, 2006, 26(7): 47-53 QIN Xu-wei, FAN Yu-shun, YIN Chao-wan. Research on Hybrid Particle Swarm Optimization for Automobile Logistics Network Design Problem[J]. Systems Engineering-Theory & Practice, 2006, 26(7): 47-53 |
| [6] | 孙宝凤, 杨华, 韩伟. 星形整车物流联盟的收益分配机制研究[J]. 公路交通科技, 2009, 26(12): 142-147 SUN Bao-feng, YANG Hua, HAN Wei. Study on Income Distribution Mechanism in Star-like Finished Vehicle Logistics Alliance[J]. Journal of Highway and Transportation Research and Development, 2009, 26(12): 142-147 |
| [7] | 王婷, 刘峰涛. 整车汽车物流共同配送模式设计与仿真[J]. 计算机系统应用, 2011, 20(8): 122-125 WANG Ting, LIU Feng-tao. Designing and Simulation of Common Distribution Mode of Finished Vehicle Logistics[J]. Computer Systems & Applications, 2011, 20(8): 122-125 |
| [8] | 张磊, 袁建清, 郑磊. 汽车整车配载与运输路线优化方案及算法研究[J]. 计算机技术与发展, 2011, 21(6): 219-222 ZHANG Lei, YUAN Jian-qing, ZHENG Lei. Methods and Algorithm Research for Motor Vehicle Loading and Transportation Route Optimizing[J]. Computer Technology and Development, 2011, 21(6): 219-222 |
| [9] | CESCHIA S, DI GASPERO L, SCHAERF A. Tabu Search Techniques for the Heterogeneous Vehicle Routing Problem with Time Windows and Carrier-dependent Costs[J]. Journal of Scheduling, 2011, 14(6): 601-615 |
| [10] | 戢晓峰, 普永明, 梁斐雯, 等. 交通管制时限条件下城市物流配送优化双层规划模型[J]. 公路交通科技, 2014, 31(12): 145-152 JI Xiao-feng, PU Yong-ming, LIANG Fei-wen, et al. Bi-level Programming Model for City Logistics Distribution Optimization under Time Restrict Condition Caused by Traffic Control[J]. Journal of Highway and Transportation Research and Development, 2014, 31(12): 145-152 |
| [11] | 钱丹, 刘建胜, 袁彬, 等. 多车型联运整车物流配送优化模型及算法研究[J]. 制造业自动化, 2015, 37(3): 65-68, 72 QIAN Dan, LIU Jian-sheng, YUAN Bin, et al. Study on Finished Vehicle Logistics Optimization Based on Multi-types Carrier'S Collaborative Distribution[J]. Manufacturing Automation, 2015, 37(3): 65-68, 72 |
| [12] | 侯玉梅, 贾震环, 田歆, 等. 带软时间窗整车物流配送路径优化研究[J]. 系统工程学报, 2015, 30(2): 240-250 HOU Yu-mei, JIA Zhen-huan, TIAN Xin, et al. Research on the Optimization on the Vehicle Logistics Distribution with Soft Time Windows[J]. Journal of Systems Engineering, 2015, 30(2): 240-250 |
| [13] | 熊军军. 基于贪婪和禁忌搜索策略的乘用车运输计划问题的研究[D]. 武汉: 华中师范大学, 2015. XIONG Jun-jun. A Research for Passenger Car Transportation Planning Problem Based on Greedy and Tabu Search[D]. Wuhan: Central China Normal University, 2015. |
| [14] | 钱丹, 刘建胜, 袁彬, 等. 多车型联运整车物流配送优化模型及算法研究[J]. 制造业自动化, 2015, 37(3): 65-68, 72 QIAN Dan, LIU Jian-sheng, YUAN Bin, et al. Study on Finished Vehicle Logistics Optimization Based on Multi-types Carrier's Collaborative Distribution[J]. Manufacturing Automation, 2015, 37(3): 65-68, 72 |
| [15] | 李金夫, 庹先国, 刘勇, 等. 关于整车物流运输车辆路径优化设计的研究[J]. 计算机仿真, 2016, 33(4): 184-188 LI Jin-fu, TUO Xian-guo, LIU Yong, et al. Study on Vehicle Routing Problems in Logistics Distribution[J]. Computer Simulation, 2016, 33(4): 184-188 |
| [16] | 张远, 余依. 模拟退火算法在整车物流问题中的应用[J]. 物流科技, 2016, 39(12): 81-84 ZHANG Yuan, YU Yi. The Application of Simulated Annealing Algorithm of Finished Car Logistics[J]. Logistics Sci-Tech, 2016, 39(12): 81-84 |
| [17] | 窦莉薇. 基于改进蚁群算法的A公司整车物流多式联运路径问题研究[D]. 天津: 天津师范大学, 2016. DOU Li-wei. A Study of Vehicle Logistics Multimodal Transportation Path Problem of Company A Based on Improved Ant Colony Algorithm[D]. Tianjin: Tianjin Normal University, 2016. |
| [18] | 齐心. 基于综合启发式算法的物流配送路径优化研究[J]. 物流科技, 2017, 40(1): 102-105 QI Xin. Research on Optimization of Logistics Distribution Route Based on Integrated Heuristic Algorithm[J]. Logistics Sci-Tech, 2017, 40(1): 102-105 |
 2017, Vol. 34
2017, Vol. 34
