扩展功能
文章信息
- 殷志祥, 高哲, 冯瑶
- YIN Zhi-xiang, GAO Zhe, FENG Yao
- 车辆荷载下多车道横向折减系数的计算和分析
- Calculation and Analysis of Multi-lane Transverse Reduction Factor under Vehicle Load
- 公路交通科技, 2017, 34(6): 99-105
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(6): 99-105
- 10.3969/j.issn.1002-0268.2017.06.015
-
文章历史
- 收稿日期: 2016-06-07
2. 锦州市开发区财政投资评审中心, 辽宁 锦州 121000
2. Financial Investment Assessment Center of Jinzhou Urban Development Zone, Jinzhou Liaoning 121000, China
桥梁是公路工程的重要设施,在交通运输中占有重要的地位。公路桥梁结构设计过程中经常遇到多车道的布置,在公路桥梁荷载效应计算时所采用的多车道横向折减是国际通用的设计方法,这是由于车辆荷载在横向满载时出现的概率较小,设计时应进行折减。车辆荷载多车道横向折减系数取决于桥梁多车道上行驶的车辆荷载使桥梁某一截面产生最大效应时同时处于最不利位置的可能性[1],作用在桥梁结构上的车辆荷载受时间、车重、车速、轴重、轴距等多种因素的影响,因此,建立合理的车辆荷载模型是非常重要的。文献[2]提出车辆荷载概率分布服从双峰正态分布,通过滤过泊松描述一般运行状态车辆荷载的随机过程。文献[3]提出京沪高速公路段实测车辆荷载采用1个极值Ⅰ型分布和2个正态分布的加权和模拟交通荷载状况。文献[4]列出了各国车辆荷载及车道荷载的标准规定,并分析了车辆荷载在服从正态分布时多车道横向折减系数的概率分析方法。随着我国经济的飞速发展,交通量日益增长,重载车辆相继出现,车辆荷载的概率模型已不再服从单一的正态分布,因此,有必要重新对公路桥梁多车道横向折减系数进行研究。文中基于我国主要干道上的车辆荷载实测数据,分析车辆荷载的总体分布、截尾分布以及不同设计使用年限内车辆荷载的概率分布,从而对车辆荷载在服从非正态分布时的多车道横向折减系数进行研究。
1 车辆荷载概率模型桥梁上的车辆荷载是一个随机过程,其任意时刻的车辆重量、车间距都是服从一定分布的随机变量[5]。文中基于我国主要干道(7个测点)的车辆荷载实测数据,建立车辆荷载的概率分布模型。
1.1 车辆总重概率模型国内外相关研究发现,部分车型的车辆总重呈多峰分布[6-9]。各国学者通常采用经验分布法[10]、多峰分布拟合[11-13]、车辆总重分布的主体与尾部分开拟合法[14-15]、分段多项式拟合法[16]等确定车辆荷载的概率分布模型。由图 1可以看出,采用1个对数正态概率密度函数和3个正态概率密度函数的加权和能很好描述车辆荷载的概率密度函数,即:
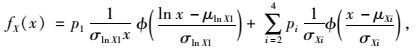
|
(1) |
式中,φ(·)为标准正态随机变量的概率密度函数;μlnX1,σlnX1为对数正态随机变量的平均值和标准差;μXi,σXi为正态随机变量的平均值和标准差;pi为系数,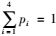
相应的车辆荷载概率分布函数为:
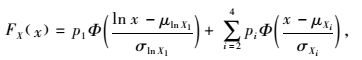
|
(2) |
式中Φ(·)为标准正态随机变量的概率分布函数。
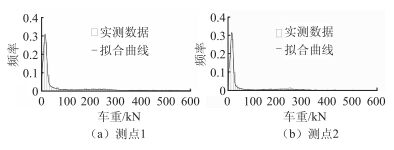
根据各测点的车辆荷载实测数据,采用极大似然法对式(1) 中的参数μlnX1,σlnX1,μXi,σXi和pi进行估计,得到的结果见表 1,取显著性水平α=0.05,经K-S检验,车辆荷载不拒绝服从多峰分布。图 1为部分测点车辆荷载统计直方图与相应的概率密度拟合曲线。
|
| 图 1 车辆荷载总体概率密度拟合曲线 Fig. 1 Fitting curves of overall probability density of vehicle loads |
| |
| 测点 | 拟合参数 | |||||||||||
| p1 | μlnX1 | σlnX1 | p2 | μX2 | σX2 | p3 | μX3 | σX3 | p4 | μX4 | σX4 | |
| 1 | 0.35 | 3.13 | 1.25 | 0.37 | 17.17 | 5.75 | 0.16 | 231.84 | 70.48 | 0.12 | 456.72 | 159.82 |
| 2 | 0.34 | 3.08 | 1.29 | 0.39 | 15.60 | 5.12 | 0.16 | 225.91 | 63.53 | 0.11 | 437.07 | 136.14 |
| 3 | 0.35 | 2.86 | 1.03 | 0.37 | 15.07 | 4.66 | 0.18 | 211.34 | 79.31 | 0.10 | 450.88 | 209.88 |
| 4 | 0.38 | 2.83 | 1.06 | 0.35 | 15.85 | 5.17 | 0.18 | 216.32 | 76.81 | 0.10 | 454.84 | 205.07 |
| 5 | 0.37 | 3.38 | 1.30 | 0.43 | 16.99 | 6.23 | 0.12 | 231.80 | 62.47 | 0.08 | 436.17 | 146.34 |
| 6 | 0.36 | 3.32 | 1.35 | 0.43 | 17.05 | 6.16 | 0.13 | 232.98 | 66.28 | 0.08 | 446.59 | 148.34 |
| 7 | 0.35 | 3.19 | 1.04 | 0.41 | 17.45 | 6.10 | 0.15 | 237.77 | 72.26 | 0.09 | 466.28 | 170.60 |
由图 1可以看出,车辆总重概率密度函数由1个对数正态概率密度函数和3个正态概率密度函数的加权和较好地反映了实测结果,即车辆荷载总体的概率密度函数曲线具有多峰性的特点。
1.2 车辆荷载截尾概率模型图 1中的概率密度函数是基于全部车辆荷载数据而言的,反映了全部车辆荷载的特点,特别是出现频率较高的车辆荷载。但对出现频率较低、车辆荷载较大的尾部反映较差,而重车荷载是影响公路桥梁安全的主要原因,为了既能反映车辆荷载的整体概率特性,又能合理反映其尾部特性,将车辆荷载的概率密度用分段函数描述。
选定荷载w,小于w的荷载用式(3) 表示的概率分布函数的右截尾函数描述,即:
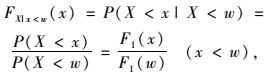
|
(3) |
式中F1(x)为右截尾概率分布函数;F1(w)为荷载w对应的右截尾概率分布函数值。
相应的概率密度函数为:
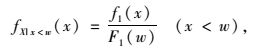
|
(4) |
式中f1(x)为右截尾概率密度函数。
大于w的荷载用式(5) 所示的概率分布函数的左截尾函数描述,即
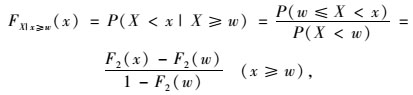
|
(5) |
式中,F2(x)为左截尾概率分布函数; F2(w)为荷载w对应的左截尾概率分布函数值。
相应的概率密度函数为:
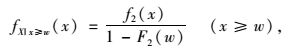
|
(6) |
式中f2(x)为左截尾概率密度函数。
式(4) 和式(6) 是截尾的概率密度函数,不是全部车辆荷载的概率密度函数,全部车辆荷载的概率密度函数按式(7)、(8) 确定:
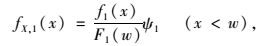
|
(7) |
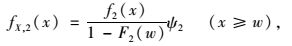
|
(8) |
式中,P(X<w)=ψ1;P(X≥w)=ψ2;ψ1+ψ2=1。
假设w值后,采用极大似然法确定式(4) 和式(6) 中的参数,并进行拟合优度检验,w值根据左截尾概率密度函数与右截尾概率密度函数在w点处连续,即fX, 1(w)=fX, 2(w)的条件确定。
基于实测车辆荷载数据,分析车辆荷载的截尾分布。假定右截尾服从1个极值Ⅰ型概率密度函数和2个正态概率密度函数的加权和,左截尾服从对数正态概率密度函数,即:
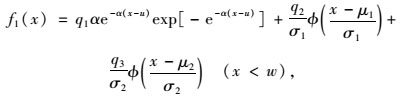
|
(9) |
式中,α和u为极值Ⅰ型分布参数;μ1,σ1,μ2,σ2为正态分布参数;q1,q2,q3为1个极值Ⅰ型分布和2个正态分布出现的概率,q1+q2+q3=1。

|
(10) |
式中μ,σ为对数正态分布参数。
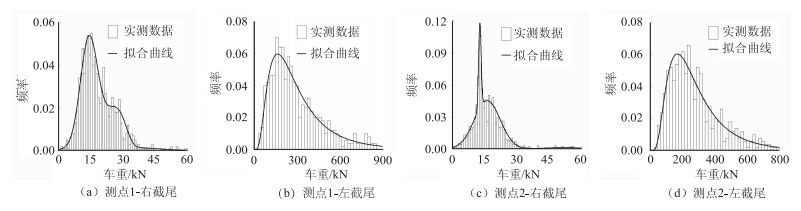
根据式(7)~(10) 计算的车辆荷载左、右截尾概率密度拟合参数见表 2,相应的概率密度拟合曲线见图 2。
| 测点 | w | 右截尾 | 左截尾 | |||||||||||
| ψ1 | q1 | α | u | q2 | μ1 | σ1 | q3 | μ2 | σ2 | ψ2 | μ | σ | ||
| 1 | 61 | 0.63 | 0.10 | 0.02 | 10.01 | 0.39 | 13.17 | 3.14 | 0.51 | 21.38 | 6.69 | 0.37 | 5.52 | 0.69 |
| 2 | 71 | 0.64 | 0.12 | 0.02 | 13.80 | 0.75 | 16.52 | 6.20 | 0.13 | 12.76 | 0.68 | 0.36 | 5.51 | 0.58 |
| 3 | 57 | 0.66 | 0.09 | 0.02 | 9.55 | 0.52 | 12.35 | 3.47 | 0.39 | 20.03 | 5.84 | 0.34 | 5.38 | 0.70 |
| 4 | 58 | 0.66 | 0.08 | 0.02 | 8.92 | 0.47 | 12.38 | 3.31 | 0.45 | 20.82 | 6.25 | 0.34 | 5.41 | 0.70 |
| 5 | 61 | 0.68 | 0.09 | 0.02 | 9.96 | 0.41 | 12.86 | 3.28 | 0.49 | 21.97 | 6.74 | 0.32 | 5.43 | 0.73 |
| 6 | 60 | 0.68 | 0.09 | 0.02 | 9.53 | 0.40 | 12.87 | 3.20 | 0.51 | 21.62 | 6.63 | 0.32 | 5.42 | 0.74 |
| 7 | 62 | 0.69 | 0.09 | 0.02 | 9.55 | 0.49 | 22.52 | 6.79 | 0.43 | 13.32 | 3.53 | 0.31 | 5.47 | 0.72 |
|
| 图 2 车辆荷载右、左截尾概率密度拟合曲线 Fig. 2 Fitting curves of right and left truncated probability density of vehicle load |
| |
1.3 设计基准期最大值概率分布
确定桥梁荷载标准值采用的是设计基准期内车辆荷载最大值的概率分布,因此需要将车辆荷载的截口分布转化为设计基准期内最大值的概率分布。
《公路工程结构可靠度设计统一标准》[17]规定,公路桥梁的设计基准期为100 a,则由式(1) 确定的设计基准期100 a车辆荷载最大值的概率密度函数为:
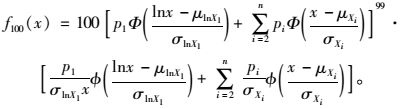
|
(11) |
由式(8) 确定的设计基准期100 a车辆荷载左截尾最大值的概率密度函数为
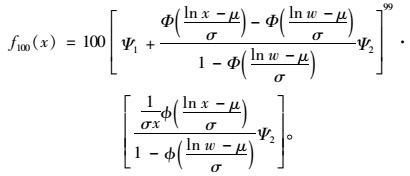
|
(12) |
为分析设计基准期内车辆荷载的统计规律,分别对式(11)、(12) 用蒙特卡洛法(M-C法)[18]生成1 000个随机数,假定概率分布类型为对数正态分布、正态分布、伽马分布,然后采用极大似然估计法拟合并进行K-S检验,最终选用对数正态分布描述设计基准期内车辆荷载的概率分布,设概率密度函数为:
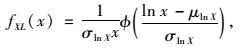
|
(13) |
式中,μlnX,σlnX分别为对数正态随机变量的平均值和标准差。
相应的概率分布函数为
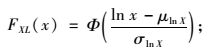
|
(14) |
平均值为
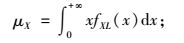
|
(15) |
方差为
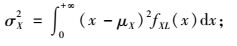
|
(16) |
变异系数为
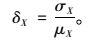
|
(17) |
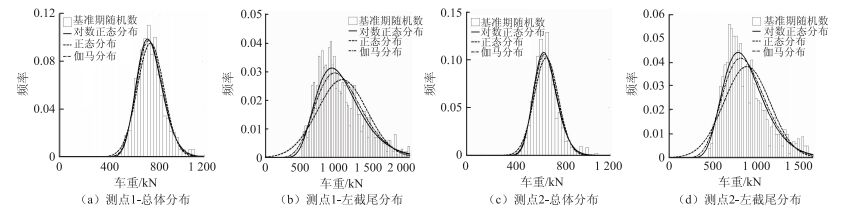
图 3给出了设计基准期内车辆荷载统计直方图和相应的拟合曲线。利用式(15)~(17) 计算设计基准期内车辆荷载最大值的平均值、标准差和变异系数,见表 3。
|
| 图 3 设计基准期内车辆荷载概率密度拟合曲线 Fig. 3 Fitting curves of probability density of vehicle load in design reference period |
| |
| 测点 | 车辆荷载总体分布 | 车辆荷载左截尾分布 | ||||||||||
| μlnX | σlnX | μX | σX | δX | Wmax | μlnX | σlnX | μX | σX | δX | Wmax | |
| 1 | 6.58 | 0.15 | 727.68 | 112.73 | 0.16 | 1 028.90 | 6.97 | 0.29 | 1 073.87 | 326.60 | 0.30 | 2 091.70 |
| 2 | 6.50 | 0.14 | 668.25 | 93.34 | 0.14 | 914.50 | 6.73 | 0.26 | 849.69 | 225.27 | 0.27 | 1 517.20 |
| 3 | 6.63 | 0.17 | 765.97 | 134.29 | 0.18 | 1 130.90 | 6.84 | 0.32 | 958.13 | 316.01 | 0.33 | 1 980.60 |
| 4 | 6.63 | 0.17 | 764.55 | 130.14 | 0.17 | 1 116.70 | 6.85 | 0.30 | 972.25 | 297.54 | 0.31 | 1 901.40 |
| 5 | 6.50 | 0.18 | 674.73 | 118.99 | 0.18 | 998.40 | 6.91 | 0.29 | 1 025.87 | 309.18 | 0.30 | 1 987.90 |
| 6 | 6.54 | 0.17 | 698.97 | 116.12 | 0.17 | 1 012.20 | 6.93 | 0.30 | 1 043.89 | 322.43 | 0.31 | 2 058.10 |
| 7 | 6.58 | 0.15 | 731.72 | 111.12 | 0.15 | 1 027.90 | 6.93 | 0.30 | 1 039.45 | 323.68 | 0.31 | 2 061.30 |
车辆荷载标准值是按设计基准期内最不利作用的某个统计特征值确定的,统计特征值一般采用概率分布的某一分位值(近似取95%分位点所对应的数值)。由式(18) 确定设计基准期内车辆荷载的最大值(车辆荷载标准值),计算结果如表 3所示。
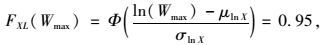
|
(18) |
式中,Wmax为设计基准期内车辆荷载的最大值(车辆荷载标准值);μlnX,σlnX按表 3取值。
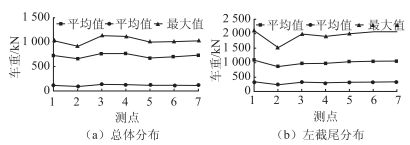
图 4为各测点车辆荷载设计基准期内的最大值与平均值、标准差关系曲线。
|
| 图 4 车辆荷载设计基准期内的最大值与平均值、标准差关系 Fig. 4 Relationships of maximum with mean and standard deviation of vehicle load in design reference period |
| |
由图 4可以看出,设计基准期内车辆荷载的最大值与平均值、标准差大致成线性关系,即车辆荷载最大值Wmax可由平均值μX和标准差σX线性表示。
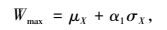
|
(19) |
式中,α1为系数,当对车辆荷载总体分布拟合时,α1=2.688;当对车辆荷载截尾分布拟合时,α1=3.122。
2 多车道横向折减系数计算《公路桥涵设计通用规范》[1]规定多车道横向折减系数即在桥梁多车道上行驶的汽车荷载使桥梁构件的某一截面产生最大效应时,其同时处于最不利位置的可能性的大小,即:
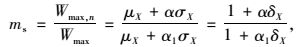
|
(20) |
式中,δX为车辆荷载变异系数,当对车辆荷载总体分布拟合时,δX=0.162;当对车辆荷载截尾分布拟合时,δX=0.304。α为参数。
假定每天有24 h的交通量通过,重车一天在n个车道上最不利位置同时出现的次数:
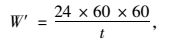
|
(21) |
式中t为重车前、后轴通过最不利位置的时间。
T年内重车一天在n个车道上最不利位置同时出现的次数:
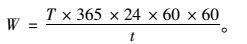
|
(22) |
q(α)为车重大于Wα的全部重车出现的概率,假设每日的交通量为Q,则重车通过影响线峰值所需总时间为:
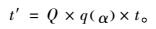
|
(23) |
一天24 h内一个车道上出现重车大于Wα的概率为:
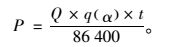
|
(24) |
《公路桥涵设计通用规范》[1]规定各车道上汽车荷载加载是互不相关的,按重复独立试验随机事件的概率理论,建立多车道横向折减系数与相关变量的关系式, 从而可得一天24 h内n个车道上同时出现重车大于Wα的概率,即:
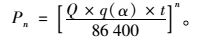
|
(25) |
设计基准期内,试验次数W很大,而n个车道上同时出现重车大于Wα的概率Pn很小,因而,用泊松分布的概率代替二项分布的概率,即:λ=W·Pn。文献[8]给出,λ=0.051 3时事件不发生的概率为95%,即:
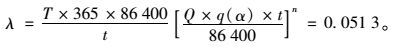
|
(26) |
整理式(26),即:
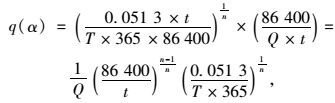
|
(27) |
式中n为车道数目。
特殊,当T=100时,式(27) 可简化为:
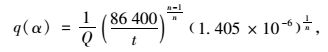
|
(28) |
式中,t=s/v,轴距s按《公路桥涵设计通用规范》[1]取12.8 m,行车速度v按实测数据取v=71.21 km/h,从而计算得出t=0.65 s,式(28) 可简化为:

|
(29) |
取n=3~8车道,车流量Q取300,500,1 000,1 500,2 000 veh/(d·ln),根据式(29) 计算q(α),通过正态分布表查出参数α,代入式(20) 计算ms,计算结果见表 4。
| 车流量/ [veh·(d·ln)-1] | 折减系数 | 车道数 | |||||||||||
| 3 | 4 | 5 | 6 | 7 | 8 | ||||||||
| Q=300 | α | 1.793 | 0.778 | -0.271* | — | — | — | ||||||
| ms | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | |
| 0.899 | 0.793 | 0.784 | 0.634 | 0.666 | 0.471 | — | — | — | |||||
| Q=500 | α | 2.016 | 1.122 | 0.347 | -0.514* | — | — | ||||||
| ms | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | |
| 0.924 | 0.827 | 0.823 | 0.688 | 0.736 | 0.567 | 0.639 | 0.433 | — | — | ||||
| Q=1 000 | α | 2.292 | 1.51 | 0.907 | 0.390 | -0.101* | -0.636* | ||||||
| ms | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | |
| 0.955 | 0.871 | 0.867 | 0.749 | 0.799 | 0.655 | 0.741 | 0.574 | 0.685 | 0.497 | 0.625 | 0.414 | ||
| Q=1 500 | α | 2.442 | 1.71 | 1.168 | 0.732 | 0.358 | 0.021 | ||||||
| ms | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | |
| 0.972 | 0.894 | 0.890 | 0.780 | 0.828 | 0.695 | 0.779 | 0.627 | 0.737 | 0.569 | 0.699 | 0.516 | ||
| Q=2 000 | α | 2.544 | 1.842 | 1.334 | 0.938 | 0.613 | 0.335 | ||||||
| ms | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | |
| 0.984 | 0.910 | 0.905 | 0.800 | 0.847 | 0.721 | 0.803 | 0.659 | 0.766 | 0.609 | 0.734 | 0.565 | ||
| 注:1表示车辆荷载总体分布;2表示车辆荷载截尾分布;带*号的数说明交通量Q相对于车道数过小。 | |||||||||||||
从而可以得出多车道横向折减系数的建议值,见表 5。
由表 5可以看出,基于实测车辆荷载计算的多车道横向折减系数比规范规定的数值偏大,这是因为随着我国经济的发展,大型运输车辆、超载车辆及交通量都有所增加,重车在车道最不利位置同时出现的概率较大,所以导致多车道横向折减系数越大。
3 结论文中基于实测车辆荷载数据,得出各测点车辆总重的总体概率分布、截尾概率分布及设计基准期内最大值的概率模型,采用概率方法计算了多车道横向折减系数,提出多车道横向折减系数的建议值。分析得出如下结论:
(1) 车辆总重的总体概率分布呈多峰分布,概率密度函数可用1个对数正态概率密度函数和3个正态概率密度函数的加权和表示;车辆荷载右截尾概率分布服从1个极值Ⅰ型概率密度函数和2个正态概率密度函数的加权和,左截尾概率分布服从对数正态概率密度函数。
(2) 设计基准期内车辆荷载最大值的概率分布服从对数正态分布。
(3) 基于实测车辆荷载数据计算的多车道横向折减系数(表 5),大于规范规定的数值。随着我国日益发展的车辆荷载及交通量的增加,多车道横向折减系数的提高比较符合我国当前交通业的发展趋势。
| [1] | JTG D60—2015, 公路桥涵设计通用规范[S]. JTG D60—2015, General Code for Design of Highway Bridges and Culverts[S]. |
| [2] | MEI G, QIN Q, LIN D J. Bimodal Renewal Processes Models of Highway Vehicle Loads[J]. Reliability Engineering and System Safety, 2004, 83(3): 333-339 |
| [3] | 郭彤, 李爱群, 赵大亮. 用于公路桥梁可靠性评估的车辆荷载多峰分布概率模型[J]. 东南大学学报:自然科学版, 2008, 38(5): 763-766 GUO Tong, LI Ai-qun, ZHAO Da-liang. Multiple-peaked Probabilistic Vehicle Load Model for Highway Bridge Reliability Assessment[J]. Journal of Southeast University: Natural Science Edition, 2008, 38(5): 763-766 |
| [4] | 张士铎. 公路桥梁车辆及车道荷载与折减系数的研究[J]. 江西科学, 2001, 19(2): 91-97 ZHANG Shi-duo. Vehicle and Lane Loading with Its Reduction Factor Study in Highway Bridge Design[J]. Jiangxi Science, 2001, 19(2): 91-97 |
| [5] | BAILEY S F. Basic Principles and Load Models for the Structural Safety Evaluation of Existing Road Bridges [D]. Lausanne: Swiss Federal Institute of Technology, 1996. |
| [6] | MIAO T J, CHAN T H T. Bridge Live Load Models from WIM Data[J]. Engineering Structures, 2002, 24(8): 1071-1084 |
| [7] | LI S, ZHU S, XU Y L, et al. Long-term Condition Assessment of Suspenders under Traffic Loads Based on Structural Monitoring System: Application to the Tsing Ma Bridge[J]. Structural Control and Health Monitoring, 2012, 19(1): 82-101 |
| [8] | 韩大建, 杜江. 工程结构作用极值分析方法研究[J]. 建筑科学与工程学报, 2008, 25(2): 68-71 HAN Da-jian, DU Jiang. Research on Extreme Value Analysis Method of Actions on Engineering Structures[J]. Journal of Architecture and Civil Engineering, 2008, 25(2): 68-71 |
| [9] | 余志武, 朱红兵, 蒋丽忠, 等. 公路桥梁车辆荷载随机过程模型[J]. 中南大学学报:自然科学版, 2011, 42(10): 3131-3135 YU Zhi-wu, ZHU Hong-bing, JIANG Li-zhong, et al. Vehicles Load Stochastic Process Model of Highway Bridges[J]. Journal of Central South University:Science and Technology Edition, 2011, 42(10): 3131-3135 |
| [10] | GETACHEW A. Traffic Load Effects on Bridges, Statistical Analysis of Collected and Monte Carlo Simulated Vehicle Data [D]. Stockholm: Royal Institute of Technology, 2003. |
| [11] | CAPRANI C C, OBRIEN E J, MCLACHLAN G J. Characteristic Traffic Load Effects From a Mixture of Loading Events on Short to Medium Span Bridges[J]. Structural Safety, 2008, 30(5): 394-404 |
| [12] | 张征文, 杨飞, 赵建峰, 等. 基于WIM数据的简支梁桥车辆荷载效应分析[J]. 公路交通科技, 2014, 31(5): 86-92 ZHANG Zheng-wen, YANG Fei, ZHAO Jian-feng, et al. Analysis on Traffic Load Effect of Simply Supported Beam Bridge Based on WIM Data[J]. Journal of Highway and Transportation Research and Development, 2014, 31(5): 86-92 |
| [13] | 孙守旺, 孙利民. 基于实测的公路桥梁车辆荷载统计模型[J]. 同济大学学报:自然科学版, 2012, 40(2): 198-204 SUN Shou-wang, SUN Li-min. Statistic Model of Vehicle Loads for Highway Bridges[J]. Journal of Tongji University:Natural Science Edition, 2012, 40(2): 198-204 |
| [14] | 蒋田勇, 谢静思. 高速公路桥梁随机荷载分布特性研究[J]. 公路交通科技, 2015, 32(7): 76-83, 91 JIANG Tian-yong, XIE Jing-si. Investigation on Distribution Characteristics of Random Loads on Expressway Bridge[J]. Journal of Highway and Transportation Research and Development, 2015, 32(7): 76-83, 91 |
| [15] | 杨东晓, 黄海云, 张俊平. 车辆荷载概率分布及其产生的荷载效应研究[J]. 广州大学学报:自然科学版, 2014, 13(5): 56-60 YANG Dong-xiao, HUANG Hai-yun, ZHANG Jun-ping. Research on the Bridge of Highway Vehicle Load Probability Distribution and Load Effect[J]. Journal of Guangzhou University:Natural Science Edition, 2014, 13(5): 56-60 |
| [16] | 冯兆祥, 张磊, 吴冲. 泰州长江大桥钢塔疲劳计算随机车辆荷载模拟[J]. 公路交通科技, 2008, 25(12): 127-131 FENG Zhao-xiang, ZHANG Lei, WU Chong. Simulation of Random Vehicle Load for Fatigue Calculation of Steel Pylon of Taizhou Yangtze River Bridge[J]. Journal of Highway and Transportation Research and Development, 2008, 25(12): 127-131 |
| [17] | GB/T50283—1999, 公路工程结构可靠度设计统一标准[S]. GB/T50283—1999, Unified Standard for Reliability Design of Highway Engineering Structures[S]. |
| [18] | CRESPO-MINGUILLÓN C, CASAS J R. A Compre-hensive Traffic Load Model for Bridge Safety Checking[J]. Structural Safety, 1997, 19(4): 339-359 |
 2017, Vol. 34
2017, Vol. 34
