扩展功能
文章信息
- 赵秋, 陈美忠, 陈孔生
- ZHAO Qiu, CHEN Mei-zhong, CHEN Kong-sheng
- 装配式空心板铰缝界面抗剪性能试验与数值模拟
- Experiment and Numerical Simulation of Shear Behavior of Interface between Hinge Joints and Precast Hollow Slabs
- 公路交通科技, 2017, 34(6): 85-93
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(6): 85-93
- 10.3969/j.issn.1002-0268.2017.06.013
-
文章历史
- 收稿日期: 2016-08-04
由于装配式空心板铰缝本身构造上的缺陷,经常出现一些病害,铰缝病害发展到一定程度会导致单板受力现象。单板受力危害很大,不但可以引起主梁病害,还可引起桥梁附属设施的病害,比如造成铺装层反射裂缝,形成桥面错台等,最终影响到桥梁的适用性和耐久性,甚至危及行车的安全。
为了改善铰缝的受力情况,避免铰缝病害发生,研究人员对铰缝构造提出了各种改进措施,如加设钢筋或钢板等,增加铰缝界面的抗剪性能。从已有的研究成果可以得知,后浇注的铰缝与预制板梁间的新旧混凝土界面抗剪强度是构成铰缝抗剪的主要因素[1]。因此,在研究新型铰缝结构或对现有应用结构的受力性能前,需掌握铰缝新旧混凝土界面抗剪性能。就目前而言,国内外对铰缝界面抗剪性能研究成果较多,但对于铰缝界面数值模拟各参数值多是给定一个范围。由此造成不同的研究者数值模拟模型在铰缝界面参数取值上有较大不同。为了确定铰缝界面数值模拟的各个参数,文中通过推出试验研究铰缝新旧混凝土界面抗剪性能,以及铰缝新旧混凝土界面抗剪数值模拟方法,来确定铰缝界面模拟各个参数的合适取值,为装配式空心板铰缝研究提供参考。
1 试验设计空心板梁桥在建造过程中,空心板为预制,铰缝为现浇,空心板梁和铰缝混凝土存在龄期差,二者黏结关系属于新旧混凝土黏结关系。该类型抗剪试验没有固定的构件形式和研究方法。国外对于该类型抗剪性能研究,大部分采用推出试验形式。
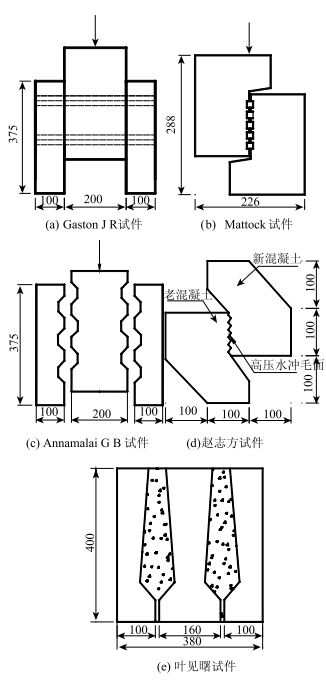
1.1 现有铰缝推出试验1964年,Gaston J R[2]通过块体的推出试验模拟通过高强螺栓锚固混凝土结构的抗剪承载力,混凝土试件由3块组成,每个混凝土预制块的接触面上设有0.03或0.06 m2贯穿孔,通过2个或4个高强度螺栓接在一起,界面滑移通过千分表来测量,如图 1(a)所示。1972年,Mattock[3]研究了电梯井机剪力墙板结合面的受剪承载力,每个试件由两个混凝土预制块组成,中间通过锯齿状的水泥砂浆连接,如图 1(b)所示。1990年,Annamalai.G.B[4]对灌浆铰缝的抗剪强度进行研究,按如图 1(c)所示的试验试件进行了推出试验,通过研究不同高度锯齿状剪力连接凹槽,提出用于评价以灌浆形式填充锯齿状剪力连接凹槽的抗剪强度。1999年,赵志方[5]采用Z字形试件对新旧混凝土结合面关系抗剪性能进行试验研究,试件示意图如图 1(d)所示。2013年,叶见曙[6]通过推出试验研究预制板铰缝抗剪性能,施加单调的试验荷载,在铰缝处形成剪切力,研究试件铰缝的受力过程和破坏形态。采用如图 1(e)所示的试验试件,试验试件分别由3块预制混凝土块拼接,铰缝后期浇注而成。
|
| 图 1 推出试验试件示意图(单位:mm) Fig. 1 Schematic diagram of specimen for push-out test (unit:mm) |
| |
1.2 试验试件设计
总结以上的试验试件形式主要可以分为两类:一类是类似Z字形的试验试件,赵志方和Mattock的试验试件都属于这一类。另外一类是凸字形的试验试件,其余的试件形式都属于这一类。对于第1种试件形式,由于其形状相对于后者来说属于异型构件,从试件制作和加载的简易程度来说,该类型试件相对后者比较麻烦。另外,后者试件形式更接近于实际桥梁形式,因此,文中采取第2种试件形式。
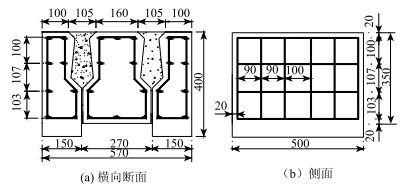
以中华人民共和国交通部公路桥涵通用图中13 m空心板为参考[7],并减小铰缝高度,这里由新型铰缝构造所决定,具体见相关专利[8]。按1:2的比例进行缩尺设计试验试件尺寸,为了使试验结果可靠,共设计了3组试件,如图 2所示。每组试件由左中右3块试件组成,试件高分别为350 mm(中间混凝土预制块)和400 mm(左右两边混凝土预制块),横向宽570 mm(平行于纸面的方向),纵向长度为500 mm(垂直于纸面的方向)。
|
| 图 2 试验试件尺寸示意图(单位:mm) Fig. 2 Dimensional figure of experimental specimen (unit:mm) |
| |
试件均采用相同的配筋率,箍筋和纵向钢筋根据整个界面的配筋率按比例进行缩尺。原标准图中整个截面的配筋率为0.52%,经缩尺后,纵向钢筋和箍筋所用钢筋直径均为8 mm。
2 试件制作与试验加载方案 2.1 试件制作对于焊件的焊接残余应力研究,以往多采用切割、钻孔等破坏性试验测量方法,首先将钢筋绑扎并固定形成钢筋骨架。之后进行模板支护、预制构件混凝土浇注及养护,形成左中右3块预制构件,最后进行铰缝周边混凝土凿毛、铰缝混凝土浇注与养护。工序流程部分图片如图 3所示。

|
| 图 3 试验模型制作流程图 Fig. 3 Flowchart of fabrication procedure of experimental model |
| |
2.2 试验加载和测点布置
根据推出试验研究的目的,在试验过程中需要测得数据有:试件结合面开裂荷载值(或应变值)、裂缝发展历程、破坏形态、试件极限荷载、结合面应变值以及试件位移值。
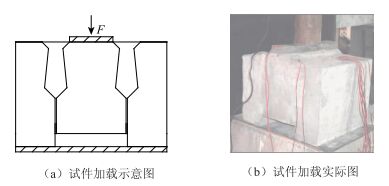
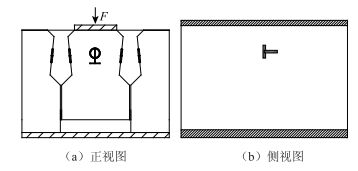
采用油压千斤顶进行推出试验,为单点集中加载方式,如图 4所示。试件测点主要有应变测点和位移测点,应变测点布置如图 5所示。其中试件表面的应变片是为了测得试件在结合面处拉应变和开裂应变。当应变片因为结合面的相对滑移导致断裂时,可得到对应的开裂荷载[1]。结合面内表面贴应变片的目的是为了测得铰缝结合面相对剪切应变。采用位移计测量中间块与铰缝的相对位移。
|
| 图 4 构件加载示意图 Fig. 4 Schematic diagram of component loading |
| |
|
| 图 5 试件测点布置图 Fig. 5 Arrangement of specimen measuring points |
| |
2.3 试验加载制度
试验加载以5 kN递增或递减,且每次施加荷载稳定后恒定3 min。试件首先需要预加载,分级加载到40%预估极限荷载,以同样速度分级卸载,如此重复2次。第2个试件,预加载和正式加载的加载方案与第1个试件相同,不同的是预估极限荷载取第一个试件测得的极限荷载。第3个试件在第1个和第2个测得极限荷载基础上进行加载。
3 试验分析 3.1 试验现象分析试件SJ-i(i=1, 2, 3) 在荷载分别达到220,215,230 kN之前,试件结合面处无明显变化,未出现裂缝。当各试件荷载值达到上述值时,沿试件铰缝结合面产生贯穿裂缝,试件瞬间破坏,如图 6(a)所示。破坏面处为新旧浇注混凝土的相交面,表面状态为铰缝浇注前的凿毛状态,如图 6(b)所示。上述3组试件在整个加载过程中结合面无明显变化,铰缝与预制混凝土仅依靠纯混凝土结合面的黏结来克服剪力作用,当达到极限强度时,试件将发生脆性破坏。

|
| 图 6 SJ-1破坏形态及结合面状态 Fig. 6 Failure form and interface condition of SJ-1 |
| |
3.2 试验结果分析
试验数据汇总如表 1所示,其中铰缝试验抗剪强度为试件极限荷载与铰缝结合面面积之比[9]。
| 试件编号 | 破坏荷载/kN | 抗剪破坏强度σu/MPa |
| SJ-1 | 220 | 1.100 |
| SJ-2 | 215 | 1.075 |
| SJ-3 | 230 | 1.150 |
| 平均值 | 221 | 1.100 |
| 标准差 | 6.24 | 0.03 |
对于结合面黏结强度的评价,Huckelbridge以空心板与铰缝相对位滑移值作为评价指标[10]。叶见曙也以同样的方式测得了平均剪应力-滑移曲线[11]。其中平均剪应力是试验过程中的试验荷载除以铰缝结合面积。
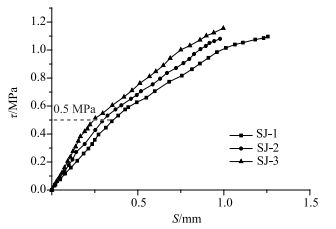
平均剪应力-滑移(τ-s)曲线近似由直线的弹性阶段和曲线的弹塑性阶段组成,如图 7所示。弹性阶段τ≤0.5 MPa,滑移值较小,平均剪应力-滑移曲线线性变化;弹塑性阶段,试件结合面内部开始时出现微裂缝,后期裂缝逐步增大,平均剪应力-滑移曲线非线性变化,斜率逐渐减小,整个线形逐渐趋于平缓。
|
| 图 7 平均剪应力-滑移曲线(τ-s曲线) Fig. 7 Average shear stress-slip curve (τ-s curve) |
| |
4 数值模拟方法 4.1 单元选取
计算对于推出试验的数值模拟,如何选用合适的单元类型是有限元数值模拟方法能否正确有效模拟实际模型的关键。单元类型的选用应该考虑单元的力学特性是否与实际构件受力性能相统一。如果能满足计算精度的要求,应尽量选择简单即低阶单元。按照文中数值模拟的需要,选取了八节点线性六面体缩减积分单元(C3D8R)模拟铰缝混凝土梁体,采用三维二节点桁架单元(T3D2) 来模拟钢筋。
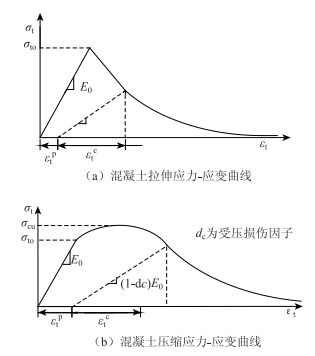
4.2 材料本构关系 4.2.1 混凝土本构关系有限元程序对于混凝土力学性能的模拟主要是根据用户输入的混凝土本构关系来确定的。因此,正确选用混凝土本构关系模型是数值模拟的重要一环。ABAQUS中应用相对较广的模型包括:损伤塑性模型、弥散裂纹模型和脆性破裂模型。脆性破裂模型对于静力模型模拟效果差,大多用于动力分析;其余两个模型对于静力问题的分析结果均较好。但是相较于弥散裂纹模型,损伤塑性模型对于单项加载的收敛性更好。损伤塑性模型是一个以塑性的连续介质为基础的本构关系模型,其模型的失效机理是拉伸开裂和压缩破碎,屈服面的演化通过两个变化量控制,分别是:拉伸和压缩等效塑性应变。其模型拉压曲线在ABAQUS中的关系如图 8所示[12]。
|
| 图 8 损伤塑性模型拉压应力应变关系曲线 Fig. 8 Tensile and compressive stress-strain relationship curves of damaged plasticity model |
| |
从图中可以看到:① 拉伸和压缩在第1阶段的应力应变关系均呈直线状态,即弹性阶段。② 二者对于进入软化阶段激活点不同,对于单轴受拉来说,当受拉材料达到屈服时,材料马上进入软化;而单轴受压不会,单轴受压会有一个屈服阶段,当应力值超过σcu才进入软化阶段。
对于损伤塑性模型中具体参数,ABAQUS没有明确规定。文中混凝土单轴受压应力-应变关系根据文献[14]中规定的素混凝土应力-应变关系来模拟,表达式如式(1) 和式(2) 所示。
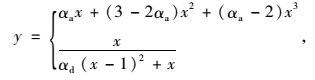
|
(1) |
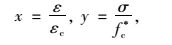
|
(2) |
式中,fc*为混凝土单轴受压轴心抗压强度标准值;εc 为与fc*相对应的混凝土峰值压应变;αa、αd为单轴受压本构关系曲线上升段和下降段的参数值,跟混凝土强度有关。
关于混凝土受拉本构关系,ABAQUS为用户提供了计算方式:应力-应变、应力-裂缝宽度和断裂能。其中断裂能的计算方式相对于其他两个更容易收敛[13]。断裂能Gf按欧洲规范CEB-PIB MC90的建议计算,如式(3) 所示。对于文中混凝土断裂能为0.15 N/mm。
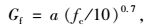
|
(3) |
式中,fc为混凝土抗压强度;Gf为断裂能。a为与最大骨料粒径Dmax有关的系数,Dmax=8 mm时,a=0.025;Dmax=16 mm时,a=0.030;Dmax=32 mm时,a=0.058。
损伤塑性模型除了应力应变关系还要确定其他参数,根据文献[14]来取值,偏移值为0.1,膨胀角35°,拉伸子午面上和压缩子午面上的第2应力不变量之比K取0.667以及黏性参数为0.005。
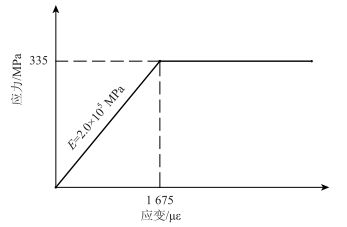
4.2.2 钢筋本构关系钢筋本构关系采用理想弹塑性模型,应力应变关系示于图 9,弹性模量Es=2.0×105 MPa,泊松比μ=0.3,屈服应力=335 MPa。
|
| 图 9 钢筋应力-应变关系 Fig. 9 Stress-strain relationship of rebar |
| |
4.3 结合面参数
空心板铰缝结合面问题按其施工工艺流程来说属于新旧混凝土黏结问题。首先该类问题其自身黏结机理到目前仍然是一个难点。结合面本身带有一定的缺陷,如结合面初始裂纹。实际上,结合面处于一种连续和离散的状态。该类型结合面的力学性能夹杂着断裂力学和结合面接触问题[15]。
(1) 结合面黏结应力
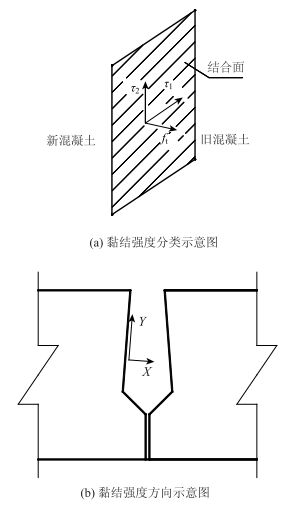
新旧混凝土结合面黏结应力包括一个法向应力ft和两个平行于结合面的剪切应力τ1和τ2,如图 10所示。图中标注出了结合面中各个应力方向,X为垂直于结合面的法向应力方向,Y是与结合面板高度方向相平行,Z是与结合面纵桥向相平行(Z方向b图未标注)。
|
| 图 10 新旧混凝土黏结应力方向示意图 Fig. 10 Schematic diagram of bond stress direction of new and old concrete |
| |
目前,对于结合面的黏结应力还没有统一的计算公式,且结合面黏结应力和很多因素有关,如结合面的表面粗糙度、增强结合面黏结的黏结增强剂和结合面处的构造钢筋等。现有的结合面的黏结应力计算公式有以下几种:美国混凝土结构设计规范、Robins和Austin的黏结模型[16]、刘健的黏结模型[17]、叶见曙的黏结模型[11]。美国混凝土结构设计规范的结合面黏结模型,未能细分法向应力与切向应力对结合面黏结应力的影响,计算结果有所欠缺;而Robins和Austin的计算公式,虽然已经考虑了较多因素,但是忽略了结合面内钢筋的影响;对于刘健的结合面黏结模型的问题也与Robins和Austin计算公式一样,公式计算囊括了大量因素对结合面黏结强度的影响,却没有考虑铰缝钢筋的影响。除此之外,上述几个公式仅仅是对新老混凝土结合面的黏结应力计算公式,而叶见曙公式是根据铰缝推出试验结果和相关的试验成果统计分析后得到。因此,该公式更能够真实体现铰缝结合面的抗剪特性。所以,文中以叶见曙的结合面黏结模型来计算结合面黏结应力强度。叶见曙等[12]针对不同铰缝构造的抗剪试验对比,参考中外学者的研究成果,通过统计分析整理出了铰缝抗剪强度的计算公式:
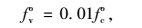
|
(4) |
式中,fvo为铰缝抗剪强度;fco为铰缝和空心板混凝土中强度值较小的混凝土轴心抗压强度值。需要指出的是试验中所发生的破坏均为空心板块体和铰缝块体的结合面破坏。
(2) 黏结滑移关系
对于结合面的黏结行为的模拟ABAQUS可以通过接触单元和基于表面的接触行为这两种方式来实现。就目前而言,使用基于表面的接触行为来模拟结合面的黏结关系,能更广泛模拟结合面黏结接触。所以文中采用基于表面的接触行为来模拟结合面的黏结滑移关系[18]。
在确定黏结滑移模拟的方式后,如何确定结合面之间的黏结滑移参数,是正确进行数值模拟基础。黏结滑移参数主要包括黏结滑移曲线的类别、结合面黏结应力的取值、结合面黏结滑移刚度以及最终滑移值。
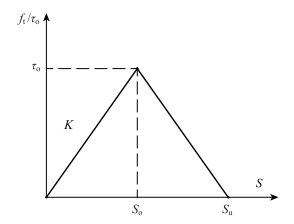
对于黏结滑移曲线类别的选择,文中主要参考刘沛林的研究结果[18],采用双折线来模拟结合面的黏结滑移关系,这也是目前在进行结合面黏结滑移关系模拟时被广泛采用的,如图 11所示。图中结合面法向黏结应力与平行于结合面的剪切应力采用的相同的黏结滑移曲线类别;结合面的黏结滑移刚度K=5~15 MPa/mm。最终滑移值与峰值应力对应的滑移值之比Su/So为:1~3。
|
| 图 11 双折线黏结滑移模型 Fig. 11 Double dogleg bond-slip model |
| |
(3) 模拟参数
1) 法向轴拉黏结强度
根据刘沛林的研究成果[18],法向轴拉黏结强度为新、旧混凝土中相对较小的轴心抗拉强度70%。铰缝与预制板均采用C40混凝土,轴心抗拉强度标准值为2.40 MPa。因此,法向轴拉黏结强度计算结果为:
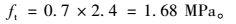
|
2) 结合面的黏结剪切强度
沿着结合面的剪切强度采用相同值,根据叶见曙的研究理论成果来计算剪切强度,结果如下式所示:
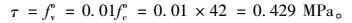
|
3) 结合面黏结滑移刚度
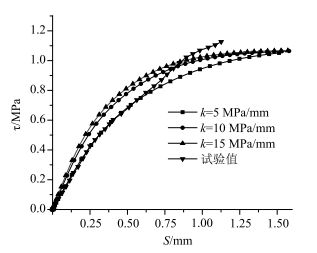
就目前而言,对3个方向的黏结强度间的耦合关系还没有相对成熟的理论研究。因此,为了了解结合面黏结滑移刚度对结合面的影响,文中采用控制变量法即保证其他参数相同,仅改变结合面黏结滑移刚度进行铰缝的有限元分析,来确定结合面黏结滑移刚度的合适取值。前文介绍了黏结滑移刚度取值范围为5~15 MPa/mm,这里选取了5,10,15 MPa/mm进行分析,得到的荷载滑移曲线与试验值进行比较,结果如图 12所示。
|
| 图 12 不同滑移刚度荷载位移曲线 Fig. 12 Load-displacement curves in different slip stiffnesses |
| |
从图 12可以看到:在初始弹性阶段,当设置的黏结滑移刚度为10 MPa/mm和15 MPa/mm,计算得到的滑移刚度荷载曲线斜率相较于试验值偏大。而黏结滑移刚度为5 MPa/mm时,计算得到的滑移刚度荷载曲线与试验值吻合较好。对于塑性阶段,3种不同黏结滑移刚度的承载力相对于试验值均偏小。虽然当滑移值小于1.5 mm时,黏结滑移刚度为5 MPa/mm的承载力相较于其他两个黏结滑移刚度值承载力偏小,但是其承载力是逐渐趋于其他两个黏结滑移刚度承载力。综合弹性阶段和塑性阶段荷载滑移曲线对比,黏结滑移刚度为5 MPa/mm模拟更为精确。
4) 滑移值之比Su/So
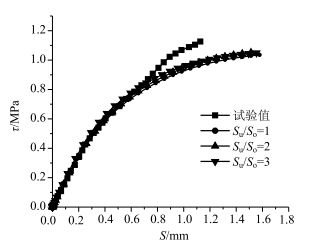
目前,对于常用最终滑移值与峰值应力对应的滑移值之比Su/So为:1~3。为了能更准确地模拟铰缝结合面接触关系,在此同样采用控制变量法来分析滑移值之比的影响,黏结滑移刚度取5 MPa/mm。结果如图 13所示。
|
| 图 13 不同滑移值之比的荷载位移曲线 Fig. 13 Load displacement curves in different ratios of slip values |
| |
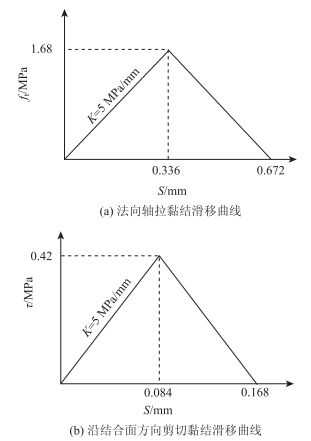
从图 13可以看到:不同滑移值的比值对结果影响不是很大。但是为了保证能更准确模拟结合面的接触关系,文中采用折中的办法保守选取比Su/So为2,则空心板与铰缝结合面各方向的黏结滑移曲线示于图 14。
|
| 图 14 空心板和铰缝结合面黏结滑移曲线 Fig. 14 Bond-slip curve for bonding interface of hollow plate and hinge joints |
| |
(4) 有限元建立
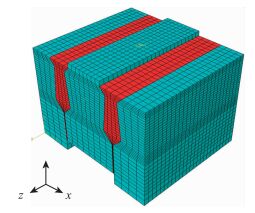
有限元模型如图 15所示:X为沿试件横向宽度方向,Y为沿试件高度方向,Z为沿试件厚度方向;模型边界为简支约束,一端释放Y方向约束,一端固结。
|
| 图 15 模型示意图 Fig. 15 Schematic diagram of model |
| |
4.4 有限模型模拟方法验证
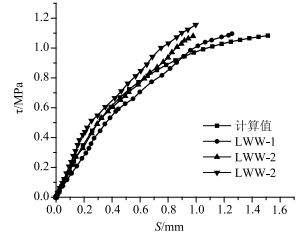
3个试验试件荷载滑移曲线取均值,与有限元计算值的荷载滑移曲线比较,两者基本吻合,见图 16。试件铰缝τ试验均值为1.1 MPa,有限元计算的τ值为1.08 MPa,计算值与试验值偏差为1.8%。因此可认为试验与有限元模拟所得的结果吻合度较好。
|
| 图 16 荷载滑移曲线对比 Fig. 16 Comparison of load-slip curves |
| |
图 17为试件有限元和试验的破坏形态对比。从图中可以看到,模型破坏是沿着铰缝结合面破坏,且结合面之间已经完全脱离。这与试验试件破坏形态是一样的。这也进一步验证了有限元模拟的正确性。

|
| 图 17 试件试验与有限元破坏形态对比 Fig. 17 Comparison of failure modes of finite element and experimental specimen |
| |
5 结论
(1) 铰缝在竖向剪力作用下,铰缝与预制混凝土仅依靠纯混凝土结合面的黏结来克服剪力作用,试件在整个受力过程中未出现裂缝,当达到极限强度时,试件将发生脆性破坏,平均τ为1.1MPa。
(2) 平均剪应力-滑移(τ-s)曲线近似由直线的弹性阶段和曲线的弹塑性阶段组成,弹性阶段τ≤0.5 MPa,滑移值较小,平均剪应力-滑移曲线线性变化;弹塑性阶段,试件结合面内部开始时出现微裂缝,后期裂缝逐步增大,平均剪应力-滑移曲线非线性变化,斜率逐渐减小,整个线形逐渐趋于平缓。
(3) 铰缝混凝土本构关系采用损伤塑性模型,钢筋本构关系采用理想弹塑性模型,新旧混凝土结合面采用面面接触技术模拟可获得较好效果,其中黏结滑移刚度取5 MPa/mm,最终滑移值与峰值应力对应的滑移值之比为2。
| [1] | 林静. 装配式板梁桥铰缝黏结抗剪性能研究[D]. 马鞍山: 安徽工业大学, 2014. LIN Jing. Study on Shear Bonding Behavior of Hinge Joint for Fabricated Plate Girder Bridge[D]. Maanshan: Anhui University of Technology, 2014. |
| [2] | GASTON J R, KRIZ L B. Connections in Precast Concrete Structures: Scarf Joints[J]. PCI Journal, 1964, 9(3): 37-59 |
| [3] | MATTOCK A H, HAWKINS N M. Shear Transfer in Reinforced Concrete: Recent Research[J]. PCI Journal, 1972, 17(2): 55-75 |
| [4] | ANNAMALAI G, CLARKE A, GERSTLE K H. Shear Strength of Post-tensioned Grouted Keyed Connections[J]. PCI Journal, 1990, 35(3): 64-73 |
| [5] | 赵志方, 赵国藩, 黄承逵. 新老混凝土黏结的拉剪性能研究[J]. 建筑结构学报, 1999, 20(6): 26-31 ZHAO Zhi-fang, ZHAO Guo-fan, HUANG Cheng-kui. Research of the Tension-shear Behavior of the Adhesion of Young and Old Concrete[J]. Journal of Building Structures, 1999, 20(6): 26-31 |
| [6] | 叶见曙, 刘九生, 俞博. 空心板混凝土铰缝抗剪性能试验研究[J]. 公路交通科技, 2013, 30(6): 33-39 YE Jian-shu, LIU Jiu-sheng, YU Bo. Experiment on Shear Property of Hinge Joints of Concrete Hollow Slab[J]. Journal of Highway and Transportation Research and Development, 2013, 30(6): 33-39 |
| [7] | 交通部专家委员会. 中华人民共和国交通行业公路桥梁通用图[M]. 北京: 人民交通出版社, 2008. Expert Committee of Ministry of Communications. General Diagram of Highway Bridge in Transport Industry of the People's Republic of China[M]. Beijing: China Communications Press, 2008. |
| [8] | 福州大学. 一种基于钢横隔板连接的装配式板桥及其施工方法: 中国, CN201310527780. 0[P]. 2014-02-05. Fuzhou University. A Fabricated Plate Bridge Based on Steel Cross-plate Connection and Construction Method: China, CN201310527780.0[P]. 2014-02-05. |
| [9] | 张婷. 混凝土空心板铰缝病害及防治措施研究[D]. 南京: 东南大学, 2011. ZHANG Ting. Study on Hinge Joint Disease of Concrete Hollow Slab and Prevention Measures[D].Nanjing: Southeast University, 2011. |
| [10] | HUCKELBRIDGE Jr. A A, El-ESNAWI H, MOSES F. Shear Key Performance in Multi Beam Box Girder Bridges[J]. Journal of Performance of Constructed Facilities, 1995, 9(4): 271-285 |
| [11] | 叶见曙, 刘九生, 俞博, 等. 空心板混凝土铰缝抗剪性能试验研究[J]. 公路交通科技, 2013, 30(6): 33-39 YE Jian-shu, LIU Jiu-sheng, YU Bo, et al. Experiment on Shear Property of Hinge Joints of Concrete Hollow Slab[J]. Journal of Highway and Transportation Research and Development, 2013, 30(6): 33-39 |
| [12] | 庄茁, 由小川. 基于abaqus的有限元分析和应用[M]. 北京: 清华大学出版社, 2008. ZHUANG Zhuo, YOU Xiao-chuan. Finite Element Analysis and Application Based on Abaqus[M]. Beijing: Tsinghua University Press, 2008. |
| [13] | GB 50010—2002, 混凝土结构设计规范[S]. GB 50010—2002, Code for Design of Concrete Structures[S]. |
| [14] | 袁明, 袁晟, 颜东煌. 预应力混凝土箱梁塑性损伤分析[J]. 公路交通科技, 2016, 33(11): 86-92 YUAN Ming, YUAN Sheng, YAN Dong-huang. Analysis on Plastic Damage of Prestressed Concrete Box Girder[J]. Journal of Highway and Transportation Research and Development, 2016, 33(11): 86-92 |
| [15] | 张楚汉. 论岩石、混凝土离散-接触-断裂分析[J]. 岩石力学与工程学报, 2008, 27(2): 217-235 ZHANG Chu-han. Discrete-contact-fracture Analysis of Rock and Concrete[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 217-235 |
| [16] | ROBINS P J, AUSTIN S A. A Unified Failure Envelope from the Evaluation of Concrete Repair Bond Tests[J]. Cement and Concrete, 1995, 47(170): 57-68 |
| [17] | 刘健. 新老混凝土黏结的力学性能研究[D]. 大连: 大连理工大学, 2000. LIU Jian. Study on Mechanics Performance of Adherence of Young on Old Concrete [D]. Dalian: Dalian University of Technology, 2000. |
| [18] | 刘沛林. 装配式钢筋混凝土简支板梁桥铰缝受力性能研究[D]. 北京: 清华大学, 2010. LIU Pei-lin. Study on Behaviors of Hinge Joints for Fabricated Reinforced Concrete Simply-supported Plate Girder Bridges[D]. Beijing: Tsinghua University, 2010. |
 2017, Vol. 34
2017, Vol. 34
