扩展功能
文章信息
- 刘小玲, 黄侨, 任远, 樊叶华
- LIU Xiao-ling, HUANG Qiao, REN Yuan, FAN Ye-hua
- 基于群组AHP的斜拉桥评估指标权重研究
- Study on Index Weight in Cable-stayed Bridge Evaluation Based on Group-AHP
- 公路交通科技, 2017, 34(6): 79-84
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(6): 79-84
- 10.3969/j.issn.1002-0268.2017.06.012
-
文章历史
- 收稿日期: 2016-04-28
2. 南京长江第三大桥有限责任公司, 江苏 南京 211808
2. Nanjing No.3 Yangtze River Bridge Co., Ltd., Nanjing Jiangsu 211808, China
斜拉桥综合评估效果的优劣对于制订桥梁养护维修方案,把握桥梁正常运营状态,具有举足轻重的作用。在斜拉桥综合评估指标体系中,指标权重体现的是各指标对于目标的重要程度,它使多指标合理地组合在一起,以实现整体最优[1-3]。因此指标权重的确定是综合评估中的关键之一。为了使决策科学化、民主化,一个复杂系统通常总是有多位专家参与决策。在用层次分析法(Analytic Hierarchy Process,简称AHP)[4-6]模型进行专家咨询时,对同一准则将获得多个判断矩阵,即所谓“群组AHP”。受知识背景的不同,以及个人偏好等因素的影响,权重的统计往往不一定是具有高度凝聚性,反而会分成几个比较鲜明的观点。以往指标权重的确定多采用简单平均方法[7],忽视了专家意见的多样性。
以南京长江三桥的指标体系权重确定为例,由于考虑了斜拉桥部件的全面性以及融入了部分健康监测数据,相较《公路桥梁技术状况评定标准》(JTG/T H21—2011)[8]而言,拟建的指标体系在数量上和内容上均有适当的增减(见图 3)。为获得一个科学、合理的综合结果,文中将在群组AHP的基础上,在标度的选择、专家综合权重的确定,以及专家意见的遴选等方面做了相应的研究,并在此基础上提出了确定大跨斜拉桥综合评估指标权重的方法。
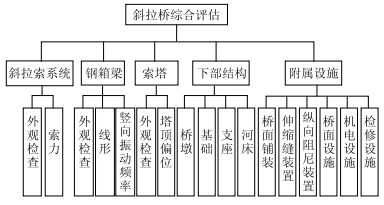
|
| 图 3 钢斜拉桥的评估指标体系 Fig. 3 Evaluation index system of steel cable-stayed bridge |
| |
1 标度方法的比较与选择
心理学家Miller的试验表明在某种属性上对若干个不同物体进行辨别时,普通人能正确辨别的物体数目在5~9个之间,因此他认为心理学上的极限应为9[9]。这表明,5个数字表述对于普通人在同时比较某种属性差异较为合理,也就是说在1~9中5个梯度的标度已可满足普通人表达分级判断的要求。因而在斜拉桥技术状态评定中拟选用五级标度。目前工程上常用的标度分为3类:1~9标度、指数标度、分数标度[10]。文中列出了4种典型的标度并进行了数值对比,见图 1。
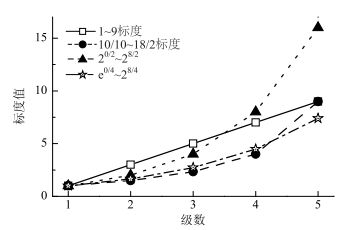
|
| 图 1 4种不同标度的数值对比 Fig. 1 Comparison of 4 scale values |
| |
参考相关文献[11]中的标度选择标准,依据图 1给出的斜拉桥指标体系构成情况,选择以下3个判断参数:一致性比率CR、标度权重拟合度F以及标度均匀性U。下面分别介绍其计算方法。
(1) 一致性比率CR能够反映构造矩阵的逻辑一致性。CR愈小,则矩阵一致性愈好。其计算公式为
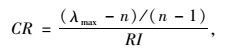
|
(1) |
式中,λmax为最大特征根;n为指标总数;RI为平均随机一致性指标,是一个既定常数。
(2) 标度权重拟合度F反映的是标度计算得到的权重与实际情况的符合度。数字标度的选择与评价应该从其与自然语言描述的符合程度出发,以能够准确表达专家的语言表述作为衡量标准[12]。中国系统工程学会层次分析法专业学组曾针对人们对于五级标度的认知差异开展过调研[13],调研分析结果如表 1所示。
| 自然语言描述 | 相同 | 稍优 | 优 | 甚优 | 极优 |
| 比率期望值s | 1.00 | 1.30 | 1.77 | 2.40 | 3.63 |
因而标度权重拟合度F可用计算权重值与期望值的差值的2范数来表示。该值愈小,表示标度之间的梯度变化与人们的认知期望更接近。标度权重拟合度F的计算公式为
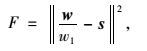
|
(2) |
式中,w为某一标度下的权重列向量;w1为最小权重值;s为比率期望值列向量,s=(1.0, 1.3, 1.77, 2.4, 3.63)T。
(3) 标度均匀性U,反映的是相邻两个标度值梯度变化的均匀程度。标度均匀性U可用相邻权重的商表示,其计算公式为
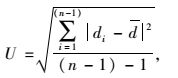
|
(3) |
式中,di为第i个相邻权重的商,di=wi+1/wi; d为平均值。
为了对照不同标度对于指标权重计算结果的影响,假设某一个评价对象Z有5个指标A,B,C,D,E,他们的关系均服从上一级比下一级稍微重要。以e0/4~e8/4标度下形成的判断矩阵为例,如表 2所示。其他标度将其替换成对应自己的标度值即可,这里不再列出。
| A | B | C | D | E | |
| A | 1.000 | 1.649 | 2.718 | 4.482 | 7.389 |
| B | 0.607 | 1.000 | 1.649 | 2.718 | 4.482 |
| C | 0.368 | 0.607 | 1.000 | 1.649 | 2.718 |
| D | 0.223 | 0.368 | 0.607 | 1.000 | 1.649 |
| E | 0.135 | 0.223 | 0.368 | 0.607 | 1.000 |
层次分析法[14]确定权重的方法有几何平均法、算数平均法、特征向量法、最小二乘法等,其中特征向量法应用最多[13]。通过该方法计算得到不同标度下的指标权重,如表 3所示。
| 指标 | 1~9标度 | 10/10~18/2 标度 | 20/2~28/2 标度 | e0/4~e8/4 标度 |
| A | 0.513 | 0.425 | 0.516 | 0.429 |
| B | 0.262 | 0.250 | 0.258 | 0.260 |
| C | 0.129 | 0.160 | 0.129 | 0.158 |
| D | 0.063 | 0.102 | 0.064 | 0.096 |
| E | 0.033 | 0.061 | 0.032 | 0.058 |
| 一致性比率CR | 0.053 | 0.005 9 | 0 | -0.000 026 |
| 标度权重拟合度F | 13.155 | 3.825 | 13.754 | 4.417 |
| 标度均匀性U | 0.053 | 0.061 | 0.001 5 | 0.000 47 |
从表 3中可以看出,1~9标度法简单、易被记忆和感知,然而其一致性和权重拟合度均相对较差。10/10~18/2标度法的标度均匀性最差;20/2~28/2标度法的标度权重拟合度最差;e0/4~e8/4标度法各项指标处于较好或最好的状态。由此可认为e0/4~e8/4标度法最为合适,1~9标度法等次之。因而文中最终选择e0/4~e8/4标度法,作为评价的标度取值。
2 指标权重的确定桥梁技术状况评价是一个复杂的评价系统。由于不同专家给出的构造矩阵一般具有多样性,通常会涉及两个主要问题:(1) 专家在考虑两两判断时,会因心理因素、知识水平等造成构造矩阵的一致性差异;(2) 群体意见有时会呈现多样化。为了反映不同专家评判结果的影响,需要考虑以上两个因素。
以往学者们在这两个方面做了不少研究[15-17]。然而他们没有区分不同类别专家的意见,有可能使得结果失真或不符合实际。
模糊C均值(Fuzzy C-means,简称FCM)聚类算法[18]是一种基于柔性的模糊划分的聚类算法,其基本思想就是使得被划分到同一簇的对象之间相似度最大,而不同簇之间的相似度最小。1973年,Bezdek提出了该算法,作为早期硬C均值聚类(HCM)方法的一种改进。FCM与HCM的主要区别在于FCM用模糊划分,使得每个给定数据点用取值在0,1间的隶属度来确定其属于各个组的程度。FCM算法既实现了专家意见的分类,同时模糊度也提供了一种度量专家意见与群体意见一致性的依据。
鉴于此,文中借鉴上述各种方法的优缺点,以FCM聚类算法为基础,对指标权重进行了分析研究,建立的指标权重的计算流程如图 2所示。
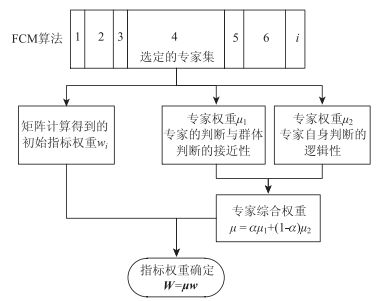
|
| 图 2 指标权重计算流程图 Fig. 2 Flowchart of calculating index weight |
| |
该流程图中的计算步骤具体如下:
(1) 确定群体意见群。首先进行FCM聚类分析,遴选出数个主要类别,然后依据“以病害多发性为主,构件重要程度为辅”的原则选定某一专家集。在实际应用中发现,隶属度小于2/3的指标权重结果已与群体意见相差甚大,因而排除这类结果。如果类别较多,离散大,则需进一步结合相关规范、专家二次讨论等方式确定。
(2) 确定专家综合权重。
文中确定专家的综合权重考虑了专家与群体判断的接近性以及专家自身判断的逻辑性。分别定义两个参数,既隶属度和专家构造矩阵的一致性指标,将两个变量进行线性函数转换,并得到第k位专家权重(μ1)k和(μ2)k,计算方法参见式(4) 和式(5)。
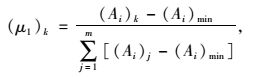
|
(4) |
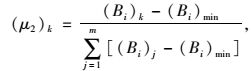
|
(5) |
式中,(Ai)k为第k位专家结果在选定类别集合里的隶属度;(Ai)min为所选类别集合中隶属度最小值;(Bi)k为反映第k位专家构造矩阵逻辑性的指标,(Bi)k=(n+2)-λmax;(Bi)min为所选类别集合中逻辑性指标最小值;m为选定类别集合中专家的数量。
使用凸组合将两者结合起来,得到其综合权重μ,计算方法参见式(6)。
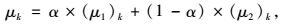
|
(6) |
式中,α为调节系数,α∈[0, 1],α越小,表示重视专家在构造矩阵中的实际表现;α越大,表示相对更信服群体判断的集中意见。文中更偏重专家自身的逻辑性,故取α=0.4[14]。
(3) 指标权重W的确定
综合所选专家的意见,最终通过加权平均得到评估指标权重集W,其计算公式为
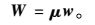
|
(7) |
文中依据南京长江三桥的病害调研信息建立的4层评估指标体系,如图 3所示。第1层为目标层,为钢结构斜拉桥综合评估,第2层为部件层,第3层为子指标层。第4层涵盖多种类型病害,由于该层计算方法不一定涉及加权平均,故在指标体系中不再列出。
本次关于权重的调查问卷投放对象包含国内大跨径桥梁养护管理单位的主要养护技术人员,设计院里的工程师以及高等院校中研究桥梁养护与加固方面的教授、研究员。共计投放问卷45份,收回43份,回收率达95.6%。经检查,有一人填写格式错误,因无法辨识而弃用,最终得到可用问卷数量是42份。
3.2 指标权重的计算以钢箱梁部件的3个子指标权重的确定为例,说明上述阐述方法的可行性及可靠性。以下简要介绍指标权重的计算过程及其结果。
(1) FCM聚类分析
使用指数标度构造相应的专家判断矩阵,并对42位专家的指标初始权重进行计算,储存每一位专家的判断矩阵的最大特征根。
钢箱梁的评价通过3个指标确定,分别是外观检查、主梁线形以及竖向振动频率。权重的计算首先应区分各类专家权重向量。在大致统计专家主流意见(2~4种)的基础上,考虑个别差异性大(2~4种)的意见,并将42组初始指标权重向量的分类数定为4类。通过引入分类数为4的参数,进行FCM聚类分析,得到前3类意见以及其所占比例分别为:第1类,59.5%;第2类,28.6%;第3类,9.5%。这3类对应的指标权重见图 4。
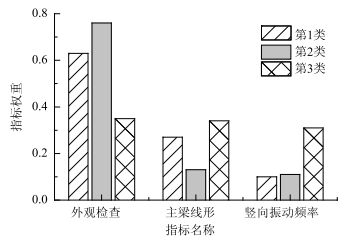
|
| 图 4 三大主要专家意见分布图 Fig. 4 Distribution of 3 major experts opinions |
| |
从图 4可以看出,第1类专家认为外观检查最重要,另外两个监测指标中主梁线形更重要;第2类专家亦认为外观检查最为重要,其他两个指标基本同等重要;第3类专家认为3个指标同等重要。综合来看,专家们主要在外观检查和监测指标以及监测指标之间的关系上出现了不同的观点。
人工检查虽然存在较大的主观性,但可直观反映结构的病害发展情况,对于钢箱梁的外观检查,锈蚀和裂纹是重要的项目,而且可随时根据需要去检查;主梁线形既可以是长期监测指标,也可以是专门检查项目,它的灵活性比较大,且该指标能较明确地反映结构整体状况;而竖向振动频率指标一般包含在监测项目内,由于这些指标长期处于安全阈值范围内,很难立刻反映出结构损伤,加之传感器的寿命有限,因而长期有效性较差。文中立足于指标直观性、检查的便捷性以及指标敏感性,侧重于人工检查和主梁线形,选定第1类专家的意见。
(2) 指标权重的确定
第1类的专家数量为25个。其中一位专家的构造矩阵的聚类隶属度为0.333,小于2/3因而被排除。由公式(4) 得到剩下24位专家的综合权重,并由公式(5) 得到钢箱梁下面的3个指标权重:
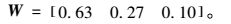
|
文中计算结果与全部42人简单平均计算结果对比如表 4所示。
| 外观检查 | 主梁线形 | 竖向振动频率 | |
| 简单平均值 | 0.55 | 0.25 | 0.20 |
| 本文方法 | 0.63 | 0.27 | 0.10 |
可以看出,简单平均的方法与文中计算结果相差较大。简单平均的方法忽视了专家意见的多样性,简单的相加使得每个权重值偏于取中间的值,各指标的权重趋于相同,没有突出不同指标的重要性,这样的结果与实际使用要求不符,因而使用价值不高。文中出于指标的敏感性、关联性和检查便捷性等考虑,首先确定3个子指标的权重相对排序,然后通过FCM算法遴选该类别中的专家,剔除了与所选权重集合差别较大的专家意见,凝聚更有针对性的结果。在所选类别中,通过加权处理融合了专家构造矩阵的合理性和群体意见的一致性,体现客观判断与“少数服从多数”的特点。因而文中的方法能得到更有效的指标权重,具有一定的实用价值。
根据上述算法,同样可以得到图 3所示指标体系第2层和第3层各项指标的所有权重,如表 5所示。
| 第2层 | 第3层 | |||||
| 斜拉索系统→ | 外观检查 | 索力 | ||||
| 0.24 | 0.80 | 0.20 | ||||
| 钢箱梁→ | 外观检查 | 线形 | 振动频率 | |||
| 0.21 | 0.63 | 0.27 | 0.10 | |||
| 索塔→ | 外观检查 | 塔顶偏位 | ||||
| 0.20 | 0.40 | 0.60 | ||||
| 下部结构→ | 桥墩 | 基础 | 支座 | 河床 | ||
| 0.28 | 0.35 | 0.40 | 0.15 | 0.10 | ||
| 附属设施→ | 桥面铺装 | 伸缩缝装置 | 纵向阻尼装置 | 桥面设施 | 检修设施 | 机电设施 |
| 0.07 | 0.35 | 0.20 | 0.15 | 0.20 | 0.05 | 0.05 |
4 结论
(1) 依据斜拉桥指标体系构成情况,选择了一致性比率CR、标度权重拟合度F以及标度均匀性U等3个判断参数。分析、计算结果表明,e0/4~e8/4标度法的各项指标处于较好或最好的状态,因而文中最终选择e0/4~e8/4标度法。
(2) 建立了一套计算指标权重计算流程。通过模糊C均值聚类算法遴选专家分类,然后考虑了专家与群体判断的接近性以及专家自身判断的逻辑性确定专家的综合权重,最后通过加权平均确定指标权重。
(3) 以斜拉桥钢箱梁的3个子指标权重的确定为例,将文中推荐方法的计算结果与简单平均方法进行了对比。结果表明,简单平均的方法忽视了专家意见的多样性,各指标权重趋于相同,没有突出不同指标的重要性。因此可认为文中方法更具针对性,计算公式中考虑专家判断的逻辑性与“少数服从多数”的特点,具有实际应用价值。按上述方法得到的指标体系及权重分配方法奠定了钢结构斜拉桥评估的基础。
| [1] | AKGUL F. Development of a Bridge Management System Incorporating a Newly Developed Model for Element Condition Evaluation Based on Damage Effects[J]. Structure and Infrastructure Engineering, 2013, 9(12): 1206-1224 |
| [2] | LIU Xiao-ling, HUANG Qiao, REN Yuan. Anomaly Detection Algorithm for Stay Cable Monitoring Data Based on Data Fusion[J]. Journal of Harbin Institute of Technology, 2016, 23(3): 39-43 |
| [3] | MOKHTARI K, REN Jun, ROBERTS C, et al. Decision Support Framework for Risk Management on Sea Ports and Terminals Using Fuzzy Set Theory and Evidential Reasoning Approach[J]. Expert Systems with Applications: An International Journal, 2012, 39(5): 5087-5103 |
| [4] | SAATY T L. Decision Making with the Analytic Hierarchy Process[J]. International Journal of Services Sciences, 2008, 1(1): 83-98 |
| [5] | HUANG Qiao, REN Yuan, LIN Yang-zi. Application of Uncertain Type of AHP to Condition Assessment of Cable-stayed Bridges[J]. Journal of Southeast University:English Edition, 2007, 23(4): 599-603 |
| [6] | MILLER G A. The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information[J]. Psychological Review, 1994, 101(2): 343-352 |
| [7] | LIU Xiao-ling, HUANG Qiao, REN Yuan, et al. Extraction of Cable Forces due to Dead Load in Cable-Stayed Bridges under Random Vehicle Loads[J]. Journal of Southeast University:English Edition, 2015, 31(3): 407-411 |
| [8] | JTG/T H21—2011, 公路桥梁技术状况评定标准[S]. JTG/T H21—2011, Standards for Technical Condition Evaluation of Highway Bridges[S]. |
| [9] | 杨帆, 苏木标, 李青宁. 采用层次分析法的不同标度计算铁路混凝土梁桥的部件权重[J]. 西安建筑科技大学学报:自然科学版, 2013, 45(2): 222-227 YANG Fan, SU Mu-biao, LI Qing-ning. Calculation on Weights of Railway Concrete Girder Bridges Parts by Several Scales in the Analytic Hierarchy Process[J]. Journal of Xi'an University of Architecture & Technology, 2013, 45(2): 222-227 |
| [10] | DONG Yu-cheng, XU Yin-feng, LI Hong-yi, et al. A Comparative Study of the Numerical Scales and the Prioritization Methods in AHP[J]. European Journal of Operational Research, 2008, 186(1): 229-242 |
| [11] | 熊立, 梁樑, 王国华. 层次分析法中数字标度的选择与评价方法研究[J]. 系统工程理论与实践, 2005, 25(3): 72-79 XIONG Li, LIANG Liang, WANG Guo-hua. Method Research on Selection and Valuation of Numeric Scale in Analytic Hierarchy Process[J]. Systems Engineering-Theory & Practice, 2005, 25(3): 72-79 |
| [12] | 朱道立, 徐庆. 运筹学[M]. 2版. 北京: 高等教育出版社, 2013. ZHU Dao-li, XU Qing. Operational Research[M]. 2nd ed. Beijing: Higher Education Press, 2013. |
| [13] | 王生昌, 陈娟娟, 田晓雪, 等. 基于层次分析法的汽车制动性能主观评价指标权重研究[J]. 公路交通科技, 2015, 32(8): 138-142 WANG Sheng-chang, CHEN Juan-juan, TIAN Xiao-xue, et al. Research on Weights of Subjective Evaluation of Automobile Braking Performance Based on AHP[J]. Journal of Highway and Transportation Research and Development, 2015, 32(8): 138-142 |
| [14] | 张忠, 方可, 杨明. 基于群组AHP的复杂仿真系统可信度评估方法[J]. 系统工程与电子技术, 2011, 33(11): 2569-2572 ZHANG Zhong, FANG Ke, YANG Ming. Method for Complex Simulation Credibility Evaluation Based on Group AHP[J]. Systems Engineering and Electronics, 2011, 33(11): 2569-2572 |
| [15] | 夏萍, 汪凯, 李宁秀, 等. 层次分析法中求权重的一种改进[J]. 中国卫生统计, 2011, 28(2): 151-154 XIA Ping, WANG Kai, LI Ning-xiu, et al. Improvement of Index Weight in Analytic Hierarchy Process[J]. Chinese Journal of Health Statistics, 2011, 28(2): 151-154 |
| [16] | 蒋田勇, 龙伟. 基于层次分析的石拱桥技术状况评定方法[J]. 公路交通科技, 2015, 32(9): 49-56 JIANG Tian-yong, LONG Wei. A Method for Evaluating Technical Condition of Stone Arch Bridge Based on AHP[J]. Journal of Highway and Transportation Research and Development, 2015, 32(9): 49-56 |
| [17] | BEZDEK J C, EHRLICH R, FULL W. FCM: The Fuzzy C-means Clustering Algorithm[J]. Computers & Geosciences, 1984, 10(2/3): 191-203 |
| [18] | 伍华成, 项贻强. 基于变权综合原理的斜拉桥索力、线形状态评估[J]. 中国铁道科学, 2006, 27(6): 42-48 WU Hua-cheng, XIANG Yi-qiang. Assessment the Cable Tension and the Linetype State of Cable-stayed Bridge Based on Variable Weight Synthesis[J]. China Railway Science, 2006, 27(6): 42-48 |
 2017, Vol. 34
2017, Vol. 34
