扩展功能
文章信息
- 张晨晨, 王旭东, 钱振东, 陈剑华
- ZHANG Chen-chen, WANG Xu-dong, QIAN Zhen-dong, CHEN Jian-hua
- 半刚性基层材料不同模量试验与分析
- Test and Analysis on Different Moduli of Semi-rigid Base Material
- 公路交通科技, 2017, 34(6): 53-60
- Journal of Highway and Transportation Research and Denelopment, 2017, 34(6): 53-60
- 10.3969/j.issn.1002-0268.2017.06.008
-
文章历史
- 收稿日期: 2016-07-15
2. 交通运输部公路科学研究院, 北京 100088
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China
模量是表征材料力学响应特性的重要参数,路面材料模量取值大小对沥青路面结构设计与分析有极大影响。由于路面材料的非均质和各向异性,路面材料具有典型的荷载依赖性,其模量受荷载条件、荷载路径、试验方法等外部因素影响[1-2]。路面材料模量按荷载模式可分为抗压回弹模量、劈裂回弹模量、拉伸回弹模量、弯拉回弹模量等; 按荷载状态又可分为静态回弹模量和动态回弹模量。
路面材料的动态模量研究始于20世纪60年代,并在90年代的Superpave设计方法中明确了SPT动态模量试验方法,其后在《AASHTO路面结构设计指南(2002)》中引入了沥青混合料动态模量,进行路面结构设计和分析[3]。虽然目前国际上路面力学分析体系仍采用静态的弹性层状体系,但由于动态模量更接近于实际路面结构中的材料响应特性,路面参数正由静态参数逐向动态参数转变。
半刚性材料作为中国传统的基层材料,具有强度高、造价低等特点,在相当长的一段时期内,半刚性基层沥青路面仍将作为一种主导性路面结构应用于中国高速公路和一般公路[4-7]。由于试验及取值方法不同,各国半刚性基层材料的模量值存在显著差异, 见表 1[8]。我国对半刚性材料参数的研究以静态为主,而对半刚性材料的动态特性相关系统研究相对较少[9]。此外由于半刚性材料的模量较大,开展半刚性材料的动态特性研究,对测试仪器的加载能力、传感器精度和数据采集能力等方面有较高要求[10]。
| 半刚性基层类型 | 中国 | 法国 | 澳大利亚 | 南非 |
| 水泥稳定碎石模量/MPa | 1 300~ 4 200 | 20 000~ 30 000 | 2 000~ 5 000 | 3 000~ 30 000 |
本文采用澳大利亚UTM材料试验机测定了3种水泥剂量的半刚性水泥稳定碎石(CBG-25) 在抗压和弯拉模式下的动、静态模量和相位角,分析了水泥剂量、应力水平、频率、测试方法等因素对半刚性基层材料模量和相位角的影响。试验结果为半刚性基层路面的设计和力学计算分析提供了依据。
1 试验材料与试件成型本文所采用水泥稳定碎石(CBG—25) 级配如表 2所示,水泥为425普通硅酸盐水泥,水泥添加剂量分别为5.5%,6.5%和7.5%。
| 筛孔/
mm | 26.5 | 19 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 |
| 质量百 分率/% | 100 | 83.7 | 69 | 57.9 | 40 | 28.2 | 19.9 | 14.2 | 10 | 7.1 | 5 |
通过标准击实试验,确定了3种半刚性基层材料的最大干密度和最佳含水量。按98%压实度静压成型3种尺寸试件:(1)φ150 mm×150 mm圆柱体试件,用于“顶面法”模量及无侧限抗压强度试验;(2)φ150 mm×170 mm圆柱体试件,用于“侧面法”模量试验;(3)100 mm×100 mm×400 mm中梁试件,用于弯拉模量及弯拉强度试验。3种材料的击实和强度试验结果如表 3所示,其模量测试具体试验方案设计见图 1。
| 水泥 剂量/ % | 最佳含 水量/ % | 干密度/ (g· cm-3) | 抗压 | 弯拉 | ||||
| 7 d强度 /MPa | 变异 系数 CV/% | 90 d 强度 /MPa | 变异 系数 CV/% | 90 d 强度/ MPa | 变异 系数 CV/% | |||
| 5.5 | 7.19 | 2.386 | 6.57 | 10.39 | 9.51 | 6.6 | 2.30 | 10.50 |
| 6.5 | 7.37 | 2.375 | 8.43 | 7.78 | 10.28 | 3.64 | 2.91 | 12.91 |
| 7.5 | 7.23 | 2.369 | 9.24 | 12.37 | 12.4 | 2.58 | 3.44 | 7.30 |
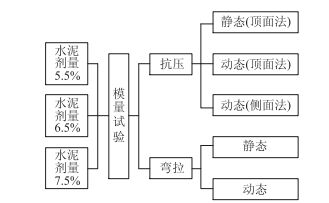
|
| 图 1 半刚性基层不同模量试验方案 Fig. 1 Experimental schemes of semi-rigid base modulus |
| |
2 半刚性基层材料模量试验方法 2.1 抗压模量试验(顶面法)
所谓“顶面法”模量试验,是将位移传感器安置在试件顶面,测量整个试件在荷载作用下变形响应。“顶面法”模量试验顶多采用径高比为1:1试件,因为试验过程相对简便,是目前最常见的模量测试方法。采用顶面法测量其试件端部会产生应力紊乱,易对变形测量产生影响,试件端部不平整也常导致较大的测量误差。
“顶面法”模量试验按荷载状态又可将之分为“顶面法”静态模量试验和“顶面法”动态模量试验。静态模量试验的加载过程一般以固定速率增加到设定荷载水平后,稳定维持1 min,然后再以相同速率完全卸载,并稳定维持30 s,静态模量试验的加载过程本质是加载了几个荷载水平不同的、频率缓慢的梯形荷载波,是某种程度上的低频动态模量试验[11]。由于车辆以一定速度驶过路面某点产生的荷载类似于半正弦波形式变化,且一般认为荷载频率为10 Hz大致相当速度70 km/h的汽车产生荷载频率,因此国际上比较通用的路面材料动态测试的加载频率为10 Hz,加载波形为半正弦波或正弦波。对于沥青混合料等黏弹特性较强材料往往还需考虑间歇时间对测试结果的影响,而半刚性材料一般不考虑间歇,通常采用连续加载。
将静压成型φ150 mm×150 mm试件,按照T0845—2009标准[12]养生90 d,按先动态后静态的顺序开展试验。试验荷载共分为8级,其中预压荷载为10 kN,其余分别为4,8,12,16,20,24 kN及28 kN。在加载金属板顶面两侧对称于圆心设置两个量程为1 mm的LVDT,测量精度为1 μm。
静态抗压回弹模量(顶面法)每级荷载加载时间为60 s,卸载间歇时间为30 s,数据采集频率为0.2 s,并分别量取每级荷载与完全卸载最后1 s的荷载与变形平均值,计算其静态回弹模量。动态抗压回弹模量(顶面法)荷载频率为10 Hz,荷载波形为Haversine波,无间歇时间,每级荷载加载200个周期,数据采集频率为0.002 s,以每级荷载最后1 s的10个周期计算其动态模量和相位角。
由图 2可知,静态模量试验在荷载保持阶段和完全卸载阶段,试件均继续产生蠕动变形,且卸载后试件未能恢复到初始状态,存在一定的塑性变形。静态回弹模量试验所测定的总回弹变形包括卸载阶段的变形和完全卸载阶段的蠕动变形。顶面法动、静态模量的试验结果如表 4所示,其中0.7 MPa结果为内插法计算所得。
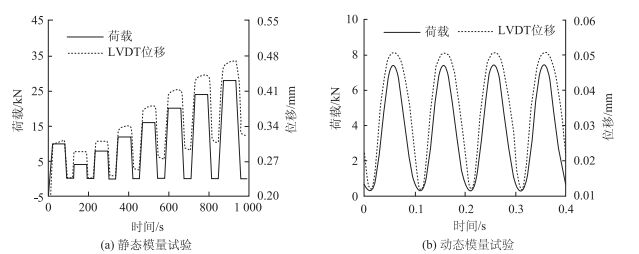
|
| 图 2 顶面法模量试验荷载-变形关系 Fig. 2 Load-deformation relationship of modulus by top measuring |
| |
| 应力水 平/MPa | 5.5%水泥剂量 | 6.5%水泥剂量 | 7.5%水泥剂量 | |||||||||
| 静态模量 /MPa | 动态模量 /MPa | 相位角 /(°) | 动/静模 量比 | 静态模量 /MPa | 动态模量 /MPa | 相位角 /(°) | 动/静 模量比 | 静态模 量/MPa | 动态模 量/MPa | 相位角 /(°) | 动/静模 量比 | |
| 0.23 | 3 097 | 6 626 | 7.2 | 2.14 | 3 384 | 7 139 | 6.1 | 2.11 | 4 044 | 7 509 | 5.8 | 1.85 |
| 0.45 | 3 145 | 7 008 | 7.0 | 2.23 | 3 501 | 7 556 | 5.9 | 2.16 | 4 197 | 7 900 | 5.7 | 1.88 |
| 0.68 | 3 195 | 7 439 | 6.6 | 2.33 | 3 627 | 8 023 | 5.6 | 2.21 | 4 367 | 8 337 | 5.2 | 1.91 |
| 0.91 | 3 247 | 7 932 | 6.2 | 2.44 | 3 765 | 8 554 | 5.4 | 2.27 | 4 556 | 8 830 | 5.1 | 1.94 |
| 1.08 | 3 301 | 8 365 | 5.7 | 2.53 | 3 914 | 9 020 | 5.2 | 2.30 | 4 768 | 9 260 | 4.7 | 1.94 |
| 1.31 | 3 359 | 9 019 | 5.6 | 2.69 | 4 079 | 9 713 | 5.0 | 2.38 | 5 007 | 9 898 | 4.1 | 1.98 |
| 1.53 | 3 419 | 9 760 | 5.4 | 2.85 | 4 260 | 10 495 | 4.9 | 2.46 | 5 279 | 10 610 | 3.8 | 2.01 |
| 0.70 | 3 200 | 7 466 | 6.5 | 2.33 | 3 657 | 8 055 | 5.5 | 2.20 | 4 386 | 8 367 | 5.1 | 1.91 |
对于同一种稳定材料,随着水泥剂量的增加,逐步从非整体性材料转变为整体性半刚性材料,其强度也不断增大,水泥剂量达到一定时也可转变为刚性材料。大量研究表明半刚性材料强度与模量之间具有良好的对应关系[13-14],由图 3知,随着水泥剂量的增加,半刚性材料的静态模量和动态模量均随之增加。在测试的荷载水平区间内,3种材料的“顶面法”所测定的相位角在3.8°~7.2°之间,并随着水泥剂量的增加,相位角逐渐减小,即随着半刚性材料强度增加,材料的黏性逐渐减弱,材料从半刚性逐步向刚性转变。
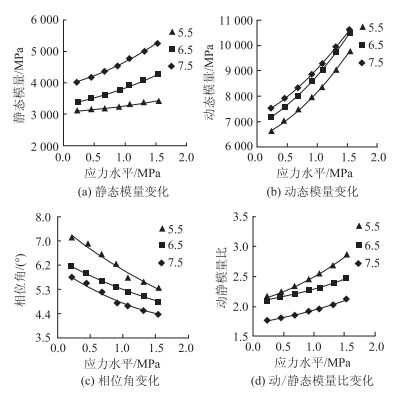
|
| 图 3 顶面法抗压模量、相位角和动/静模量比的变化 Fig. 3 Variations of compression modulus, phase angle and ratio of dynamic-static moduli by top measuring |
| |
半刚性材料作为一种典型的非线性路面材料,其模量受荷载模式以及荷载水平等因素影响,存在明显的应力依赖性。随着荷载的增加,“顶面法”动、静态模量也随之增大,材料黏弹特性中的弹性比例不断增大,相位角逐渐减小。“顶面法”动静态模量比值在1.8~2.8之间,且随着荷载不断增大。
2.2 动态抗压模量试验(侧面法)所谓的“侧面法”是相对于“顶面法”而言,通过在试件侧面安置的传感器测定试件中部的变形,避免了“顶面法”因端部应力紊乱而造成的测量误差,认为其试验结果能较好地反映材料的响应状态[15]。通常“侧面法”试件径高比一般为1:1.5。由于“侧面法”对试件尺寸及制作工艺的特殊要求,需要具备专门的成型、钻芯及切割设备,流程繁琐,成本高昂。此外“侧面法”仅测定试件中部位置变形,相比于测定整个试件变形的“顶面法”,“侧面法”对传感器量程和精度有着更高要求。由于半刚性材料模量试验是在试件潮湿状态下测定的力学响应,因此半刚性材料“侧面法”模量试验面临的另一大问题是如何在潮湿试件侧面粘贴传感器固定锚具。本文针对半刚性材料的特点提出了半刚性材料“侧面法”模量测试方法。
静压成型φ150 mm×170mm试件养生90 d后,钻芯并切割成φ100 mm×150 mm圆柱形试件,将其表面快速风干后在侧面粘置传感器固定锚具。试件浸水24 h后再开展模量测试。试件尺寸要求及传感器布置参照沥青混合料SPT动态模量试验要求[16]。一般认为试验温度对半刚性材料模量试验结果无显著影响,因此在室温20 ℃开展侧面法动态模量试验,加载频率为25,10,5,1,0.5,0.1 Hz,荷载载波形为Haversine波。
为了研究应变水平对半刚性模量的影响,采用3个应变控制水平开展测试,分别为在90~120,120~150 με及150 ~180 με。试验传感器量程为0.5mm,测量精度为0.5 μm。“侧面法”动态模量试验结果见表 5。
| 水泥剂 量/% | 频率/Hz | 90~120 με | 120~150 με | 150~180 με | ||||||
| 应力/
MPa | 动态模量/
MPa | 相位角/
(°) | 应力/
MPa | 动态模量/
MPa | 相位角/
(°) | 应力/
MPa | 动态模量/
MPa | 相位角/
(°) | ||
| 5.5 | 25 | 0.82 | 7 798 | 4.1 | 0.95 | 8 286 | 4.1 | 1.34 | 8 709 | 4.0 |
| 10 | 0.63 | 7 544 | 4.2 | 0.89 | 8 089 | 4.1 | 1.35 | 8 526 | 4.0 | |
| 5 | 0.64 | 7 435 | 4.4 | 0.83 | 8 051 | 4.2 | 1.29 | 8 335 | 4.1 | |
| 1 | 0.63 | 7 317 | 4.6 | 0.78 | 7 845 | 4.4 | 1.21 | 8 197 | 4.2 | |
| 0.5 | 0.63 | 7 226 | 4.9 | 0.81 | 7 739 | 4.7 | 1.23 | 8 065 | 4.5 | |
| 0.1 | 0.60 | 7 102 | 5.4 | 0.76 | 7 696 | 5.0 | 1.10 | 7 885 | 4.7 | |
| 6.5 | 25 | 0.79 | 9 084 | 3.8 | 1.20 | 9 420 | 3.7 | 1.69 | 9 676 | 3.7 |
| 10 | 0.65 | 8 963 | 3.9 | 1.15 | 9 294 | 3.8 | 1.65 | 9 594 | 3.8 | |
| 5 | 0.68 | 8 897 | 4.1 | 1.15 | 9 201 | 3.9 | 1.63 | 9 489 | 3.8 | |
| 1 | 0.66 | 8 772 | 4.2 | 1.16 | 9 151 | 4.1 | 1.59 | 9 314 | 4.0 | |
| 0.5 | 0.67 | 8 665 | 4.4 | 1.13 | 9 068 | 4.2 | 1.54 | 9 198 | 4.0 | |
| 0.1 | 0.63 | 8 448 | 4.7 | 1.11 | 8 885 | 4.5 | 1.47 | 8 970 | 4.3 | |
| 7.5 | 25 | 0.83 | 9 975 | 3.1 | 1.28 | 10 216 | 3.1 | 1.89 | 10 668 | 3.0 |
| 10 | 0.66 | 9 903 | 3.2 | 1.15 | 10 187 | 3.1 | 1.83 | 10 604 | 3.1 | |
| 5 | 0.66 | 9 823 | 3.2 | 1.14 | 10 115 | 3.2 | 1.82 | 10 492 | 3.1 | |
| 1 | 0.65 | 9 766 | 3.3 | 1.13 | 9 944 | 3.3 | 1.81 | 10 137 | 3.2 | |
| 0.5 | 0.64 | 9 645 | 3.5 | 1.18 | 9 869 | 3.5 | 1.78 | 10 025 | 3.4 | |
| 0.1 | 0.63 | 9 448 | 3.8 | 1.09 | 9 699 | 3.7 | 1.73 | 9 719 | 3.5 | |
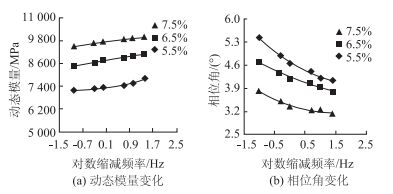
由图 4和图 5可知,“侧面法”动态模量及相位角试验结果随水泥剂量、荷载(应变)水平的变化规律,与“顶面法”动态模量试验具有一致性,不再赘述。半刚性材料在瞬间荷载作用下,材料以弹性响应为主,模量随着加载频率的增加而增大,其相位角随着加载频率的增大而减小。“侧面法”试验所测定的3种应变水平内,相位角在3.0°~5.4°之间,总体上小于“顶面法”试验结果。
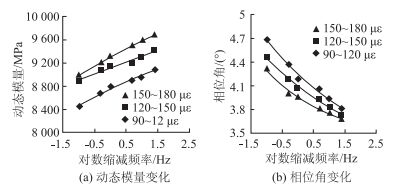
|
| 图 4 动态模量和相位角的变化(水泥剂量6.5%) Fig. 4 Variations of dynamic modulus and phase angle (cement content of 6.5%) |
| |
|
| 图 5 动态模量和相位角的变化(90~120 με) Fig. 5 Variations of dynamic modulus and phase angle (90-120 με) |
| |
2.3 弯拉模量试验
半刚性材料弯拉模量是路面设计和分析的重要参数之一,通常采用三分点加载的方法测定[17]。半刚性材料在弯拉状态下的重复加载容易产生疲劳损伤破坏,但一般认为其在小于40%~50%极限弯拉应力的重复加载条件下,半刚性材料不会产生显著的疲劳损伤[18]。本文试验为了避免重复荷载对半刚性材料的损伤,将加载应力水平控制在极限弯拉应力的35%以内。弯拉模量试验荷载设定以及数据采集计算方法均类似于“顶面法”抗压模量试验;荷载共分为8级,其中预压荷载为2.5 kN,其余分别为1,1.5,2,2.5,3,3.5 kN及4 kN。在中梁中部顶面设置一个量程为1 mm的LVDT,测量精度为1 μm。试验结果见表 6。
| 应力水 平/MPa | 水泥剂量5.5% | 水泥剂量6.5% | 水泥剂量7.5% | |||||||||
| 静态模量/
MPa | 动态模量/
MPa | 相位角/
(°) | 动/静 模量比 | 静态模量/
MPa | 动态模量/
MPa | 相位角/
(°) | 动/静 模量比 | 静态模量 /MPa | 动态模量 /MPa | 相位角/
(°) | 动/静模 量比 | |
| 0.14 | 17 600 | 23 954 | 5.6 | 1.4 | 21 343 | 25 421 | 5.1 | 1.2 | 22 704 | 28 689 | 5.0 | 1.3 |
| 0.26 | 17 376 | 23 348 | 6.3 | 1.3 | 21 047 | 25 021 | 5.9 | 1.2 | 22 453 | 27 446 | 5.5 | 1.2 |
| 0.38 | 17 168 | 22 840 | 6.7 | 1.3 | 20 762 | 24 688 | 6.0 | 1.2 | 22 211 | 26 996 | 5.6 | 1.2 |
| 0.50 | 16 974 | 22 512 | 6.7 | 1.3 | 20 490 | 24 340 | 6.3 | 1.2 | 21 969 | 26 635 | 6.0 | 1.2 |
| 0.62 | 16 791 | 21 803 | 7.0 | 1.3 | 20 242 | 24 005 | 6.6 | 1.2 | 21 746 | 26 346 | 6.3 | 1.2 |
| 0.73 | 16 627 | 21 347 | 7.1 | 1.3 | 19 990 | 23 905 | 6.8 | 1.2 | 21 560 | 25 976 | 6.4 | 1.2 |
| 0.70 | 16 660 | 21 492 | 7.1 | 1.3 | 20 053 | 23 787 | 6.7 | 1.2 | 21 599 | 26 061 | 6.4 | 1.2 |
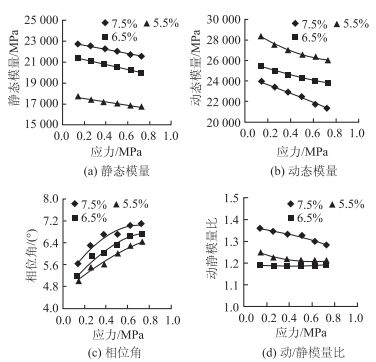
半刚性材料弯拉模量远高于抗压模量,这也体现了它的各向异性。由图 6可知,半刚性材料在弯拉状态下,依然存在明显的应力依赖性,但静态模量、动态模量以及相位角随应力水平变化的趋势,与抗压状态测定结果完全相反。弯拉模量试验所测定的相位角在5.0°~7.1°之间,并随着水泥剂量的增加,相位角逐渐减小。弯拉动静态模量比值相对稳定,基本保持在1.2~1.4之间,且随着荷载不断减小。
|
| 图 6 弯拉模量、相位角和动/静模量比的变化 Fig. 6 Variations of flexural-tensile modulus, phase angle and ratio of dynamic-static moduli |
| |
3 不同形式模量试验结果的对比分析
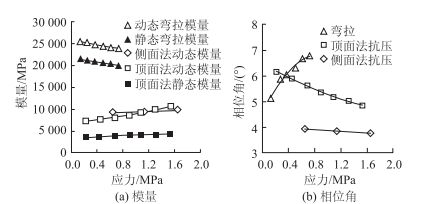
由图 7可知,“顶面法”动态抗压模量与“侧面法”动态抗压模量受力模式一致,二者的模量数值相当(侧面法动态模量取频率为10 Hz时的试验结果),但二者存在试件尺寸和传感器布置存在一定差别,二者所测的相位角相差1°~1.5°。弯拉模量试验其受力模式、试件形状完全不同于抗压模量试验,试验结果显著大于动、静态抗压模量。5种模量试验结果均表现出明显的应力依赖性,在抗压模式下半刚性基层材料的动、静态模量均随着荷载水平的增大而增大,相位角逐渐减小;而半刚性材料随弯拉荷载变化时的响应特性,与抗压模式试验结果相反。本文3种半刚性材料的应力(频率)依赖特性均可用一元二次方程来表征,其中水泥剂量6.5%时的各种模量和相位角的应力(频率)表达式见表 8。
|
| 图 7 不同模量试验下的模量和相位角比较(水泥剂量6.5%) Fig. 7 Comparison of moduli and phase angles obtained from different modulus tests (cement content of 6.5%) |
| |
| 参数 | 试验类型 | 关系式 | R2 |
| 模量 | 静态抗压(顶面法) |
E=152.84σ2+405σ+
3 284.1 | 0.982 1 |
| 动态抗压(顶面法) |
E=776.87σ2+1 181σ+
6 847.3 | 0.984 4 | |
| 动态抗压(侧面法) |
E=-4.412(lg(f))2+
204.8 lg(f)+9 111.9 | 0.986 3 | |
| 静态弯拉 |
E=314.29σ2-2 560.3σ+
21 699 | 0.964 2 | |
| 动态弯拉 |
E=-391.72σ2-4 007.7σ+
24 490 | 0.982 3 | |
| 相位角 | 动态抗压(顶面法) | φ=0.264 2σ2-1.466 7σ+6.485 8 | 0.967 5 |
| 动态抗压(侧面法) | φ= 0.041 7(lg(f))2-0.311 5lg(f) + 4.095 1 | 0.976 9 | |
| 动态弯拉 | φ=-3.015σ2+5.255 9σ+4.510 2 | 0.959 2 |
目前我国设计规范中半刚性基层材料模量值一般取0.5~0.7 MPa应力水平的对应值,并未考虑交通荷载、路面结构以及材料在实际路面中的力学响应特性,因此存在一定的局限性和不合理性。如何根据半刚性材料在实际路面中的力学响应特性,选择合适的模量应力依赖模型和模量值,是一个值得深入探讨和研究的问题。
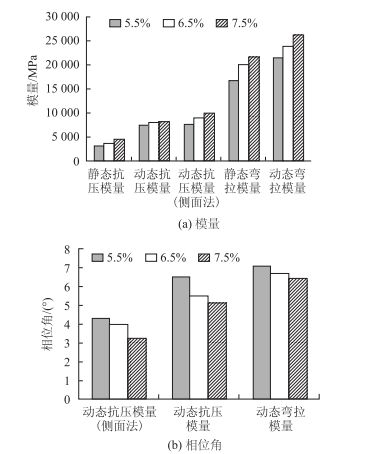
各表达式中E为模量,φ为相位角,f为加载频率。分别计算应力水平为0.7 MPa时各类模量和相位角结果,其中“侧面法”抗压动态模量取加载频率10 Hz时的试验结果。由图 8可知不同模量之间关系为:静态抗压模量<动态抗压模量<动态抗压模量(侧面法)<静态弯拉模量<动态弯拉模量;不同相位角间关系为:动态抗压(侧面法)<动态抗压(顶面法)<动态弯拉。
|
| 图 8 0.7 MPa应力水平下的不同模量试验结果对比 Fig. 8 Comparison of test results of different moduli under 0.7 MPa stress |
| |
4 结论
本文利用UTM对半刚性材料进行了多种动、静态模量室内试验,研究了水泥剂量、应力水平、加载频率及试验方法等因素对半刚性材料力学响应特性的影响,得到了以下主要结论:
(1) 半刚性材料以弹性特性为主,并具有一定的黏性和塑性。半刚性基层材料的相位角数值较小,其中“顶面法”抗压相位角为3.8°~7.2°,“侧面法”抗压相位角为3.0°~5.4°,弯拉相位角为5.0°~7.1°。
(2) 半刚性材料是一种典型的各向异性、非线性路面材料,其试验结果与试验方法、应力路径、加载频率、试件尺寸、传感器等因素有关,具有明显的应力(应变)依赖性。抗压模量随荷载、频率增大而增大,弯拉模量随荷载增加而减小;相位角变化趋势与模量变化趋势相反。因此半刚性材料模量的取值应根据其在路面结构中的实际受力特点与水平来确定。
(3) 水泥剂量是影响半刚性材料强度和响应特性的重要因素,模量随水泥剂量增加而增加,相位角随着水泥剂量增加而减小。
(4) 在试验荷载区间内,动/静抗压模量比为1.8~2.8,动/静弯拉模量比为1.2~1.4。在应力水平为0.7 MPa时,静态抗压模量<动态抗压模量(顶面法)<动态抗压模量(侧面法)<静态弯拉模量<动态弯拉模量,动态抗压(侧面法)相位角<动态抗压(顶面法)相位角<动态弯拉相位角。
由于半刚性材料存在明显的依赖性,其在实际路面中的力学响应状态,与交通荷载,路面结构等因素有关,因此传统模量取值方法存在一定的局限性。如何根据材料在路面结构中的力学响应特性选择合适的模量试验和取值方法,这一问题还有待于进一步的探讨和研究。
| [1] | 王旭东, 沙爱民, 许志鸿. 沥青路面材料动力特性与动态参数[M]. 北京: 人民交通出版社, 2002. WANG Xu-dong, SHA Ai-min, XU Zhi-hong. Dynamic Property and Parameters of Asphalt Pavement Materials[M]. Beijing: China Communications Press, 2002. |
| [2] | 姚祖康. 沥青路面结构设计[M]. 北京: 人民交通出版社, 2011. YAO Zu-kang. Structural Design of Asphalt Pavements[M]. Beijing: China Communications Press, 2011. |
| [3] | 马翔, 倪富健, 陈荣生. 沥青混合料动态模量试验及模型预估[J]. 中国公路学报, 2008, 21(3): 35-39 MA Xiang, NI Fu-jian, CHEN Rong-sheng. Dynamic Modulus Test of Asphalt Mixture and Prediction Model[J]. China Journal of Highway and Transport, 2008, 21(3): 35-39 |
| [4] | 沙庆林. 高等级公路的半刚性路面和半刚性材料的回弹模量[J]. 公路交通科技, 1991, 8(3): 1-7 SHA Qing-lin. The Semi-rigid Pavement of the High-class Roads and the Resilient Modulus of the Semi-rigid Materials[J]. Journal of Highway and Transportation Research and Development, 1991, 8(3): 1-7 |
| [5] | 沙爱民. 半刚性基层的材料特性[J]. 中国公路学报, 2008, 21(1): 1-5 SHA Ai-min. Material Characteristics of Semi-rigid Base[J]. China Journal of Highway and Transport, 2008, 21(1): 1-5 |
| [6] | 丛林, 郭忠印, 暨育雄, 等. 半刚性基层材料性能参数的试验研究[J]. 建筑材料学报, 2004, 4(4): 385-390 CONG Lin, GUO Zhong-yin, JI Yu-xiong, et al. Experimental Study on the Performance of Semi-rigid Base Coarse Materials[J]. Journal of Building Materials, 2004, 4(4): 385-390 |
| [7] | 平树江, 蒋亮, 申爱琴, 等. 半刚性材料作为长寿命沥青路面基层的适应性研究[J]. 公路交通科技, 2009, 26(4): 29-32 PING Shu-jiang, JIANG Liang, SHEN Ai-qin, et al. Research on Adaptability of Semi-rigid Material as Long Life Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development, 2009, 26(4): 29-32 |
| [8] | 沈金安. 国外沥青路面设计方法汇总[M]. 北京: 人民交通出版社, 2004. SHEN Jin-an. Summary of Abroad Asphalt Pavement Design Methods[M]. Beijing: China Communications Press, 2004. |
| [9] | 郭大进, 黑彭, 韩立志. 半刚性基层材料动态特性研究[J]. 公路交通科技, 2005, 22(12): 42-61 GUO Da-jin, HEI Peng, HAN Li-zhi. Study on Dynamic Characteristics of Semi-rigid Base Layer[J]. Journal of Highway and Transportation Research and Development, 2005, 22(12): 42-61 |
| [10] | 韦金城. 沥青路面半刚性基层材料与结构疲劳损伤研究[D]. 西安: 长安大学, 2014. WEI Jin-cheng. Research on Fatigue Damage of Semi-rigid Base Material and Structure of Asphalt Pavement[D]. Xi'an: Chang'an University, 2014. |
| [11] | 王旭东, 邓学钧, 杨树才. 半刚性材料动态模量试验的分析和研究[J]. 中国公路学报, 1998, 11(增2): 1-7 WANG Xu-dong, DENG Xue-jun, YANG Shu-cai. Analysis and Research of the Dynamic Modulus Testing for Semi-rigid Materials[J]. China Journal of Highway and Transport, 1998, 11(S1): 1-7 |
| [12] | JTG E51—2009, 公路工程无机结合料稳定材料试验规程[S]. JTG E51—2009, Test Methods of Materials Stabilized with Inorganic Binders for Highway Engineering[S]. |
| [13] | 黄卫, 钱培舒. 半刚性基层材料特性的试验研究[J]. 华东公路, 1995, 2(1): 60-63 HUANG Wei, QIAN Pei-shu. Experimental Study on Characteristics of Semi-rigid Base Materials[J]. East China Highway, 1995, 2(1): 60-63 |
| [14] | 汪水银. 半刚性基层材料动态模量研究[J]. 西部交通科技, 2009, 4(4): 9-14 WANG Shui-yin. The Study of the Dynamic Elasticity Modulus of the Semi Rigid Base Materials[J]. Western China Communications Science and Technology, 2009, 4(4): 9-14 |
| [15] | 孙立军. 沥青路面结构行为理论[M]. 上海: 同济大学出版社, 2003. SUN Li-jun. Structural Behavior Study for Asphalt Pavements[M]. Shanghai: Tongji University Press, 2003. |
| [16] | JTG E20—2011, 公路工程沥青及沥青混合料试验规程[S]. JTG E20—2011, Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering [S]. |
| [17] | 贾侃, 沙爱民, 陆剑卿. 半刚性基层材料的有效模量值[J]. 长安大学学报:自然科学版, 2009, 29(1): 15-19 JIA Kan, SHA Ai-min, LU Jian-qing. Effective Modulus Value of Semi-rigid Base Course Materials[J]. Journal of Chang'an University: Natural Science Edition, 2009, 29(1): 15-19 |
| [18] | 刘章. 半刚性材料的初期耐久性研究[D]. 重庆: 重庆交通大学, 2014. LIU Zhang. Study on Initial Durability of Semi-rigid Base Material [D].Chongqing: Chongqing Jiaotong University, 2014. |
 2017, Vol. 34
2017, Vol. 34
